Главная

Лекция 15 (продолжение). Прочность при переменных и циклически изменяющихся напряжениях

Содержание

Усталость и выносливость материалов

Основные характеристики цикла и предел усталости

Диаграмма усталостной прочности

Расчет коэффициентов запаса усталостной прочности

Влияние состояния поверхности и размеров детали на усталостную прочность

Коэффициент запаса усталостной прочности и его определение

Колебания системы с одной степенью свободы

Определение напряжений при колебаниях. Резонанс

Колебания балки с установленным на ней массивным электромотором

Степень свободы колеблющейся системы

Канонические уравнения колебания упругих систем с конечным числом степеней свободы

Собственные колебания упругих систем с конечным числом степеней свободы

Вынужденные колебания упругих систем с конечным числом степеней свободы

Приближенные методы определения низших частот собственных колебаний упругих систем

Понятие о приведенной массе

Устойчивость вращающихся валов

Колебания упругих систем при действии ударной нагрузки

Удар по конструкции вертикально движущимся телом

Удар по конструкции горизонтально движущимся телом

Продольные колебания стержня

Поперечные колебания стержня

Расчет на прочность при нерегулярной переменной нагруженности

Вопросы для самопроверки

Усталость и выносливость материалов

Многие детали машин и механизмов, а также конструкции сооружений в процессе эксплуатации подвергаются циклически изменяющимся во времени воздействиям. Если уровень напряжений, вызванный этими воздействиями, превышает определенный предел, то в материале формируются необратимые процессы накопления повреждений, которые в конечном итоге приводят к разрушению системы.

Процесс постепенного накопления повреждений в материале под действием переменных напряжений, приводящих к разрушению, называется усталостью. Свойство материала противостоять усталости называется выносливостью.

Для раскрытия физической природы процесса усталостного разрушения в качестве примера рассмотрим ось вагона, вращающуюся вместе с колесами (рис. 15.1, а), испытывающую циклически изменяющиеся напряжения, хотя внешние силы и являются постоянными величинами. Происходит это в результате того, что части вращающейся оси оказываются попеременно то в растянутой, то в сжатой зонах.

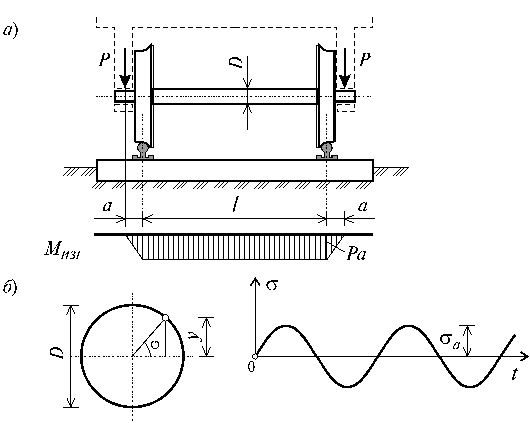
Рис. 15.1

В точке А (рис. 15.1, б) поперечного сечения оси вагона имеем:

где а - круговая частота вращения колеса. Тогда:

Таким образом, нормальное напряжение в сечениях оси меняется по синусоиде с амплитудой (рис.15.1, б):

Опыт показывает, что при переменных напряжениях после некоторого числа циклов может наступить разрушение детали, в то время как при том же неизменном во времени напряжении разрушения не происходит.

Рис.15.2

Число циклов до момента разрушения зависит от величины и меняется в весьма широких пределах. При больших напряжениях для разрушения бывает достаточно 5-10 циклов. Это хорошо видно хотя бы на примере многократного изгиба куска проволоки (рис.15.2).

При меньших напряжениях деталь выдерживает миллионы и миллиарды циклов, а при еще меньших — способна работать неограниченно долго.

После разрушения на поверхности излома детали обнаруживаются обычно две ярко выраженные зоны (рис.15.3 и 15.4). В одной зоне кристаллы различаются невооруженным глазом с большим трудом. Поверхность излома имеет сглаженные очертания. В другой зоне явно выступают признаки свежего хрупкого разрушения. Кристаллы имеют острую огранку и блестящую чистую поверхность.

В целом создается первое впечатление, что подобного рода разрушение связано с изменением кристаллической структуры металла. Именно этим и объяснялось в свое время разрушение при циклических напряжениях. Описанное явление получило тогда название усталости, а направление исследований, связанных с прочностью, стало называться усталостной прочностью. В дальнейшем точка зрения на причины усталостного разрушения изменилась, но сам термин сохранился.

В настоящее время установлено, что структура металла при циклических нагрузках не меняется. Начало разрушения носит чисто местный характер и во многом связан с неоднородностью реальной структуры материалов (различие размеров, очертаний, ориентации соседних зерен металла; наличие различных включений – шлаков, примесей; дефекты кристаллической решетки, дефекты поверхности материала – царапины, коррозия и т. д.). В связи с указанной неоднородностью при переменных напряжениях на границах отдельных включений и вблизи микроскопических пустот и различных дефектов возникает концентрация напряжений, которая приводит к микропластическим деформациям сдвига некоторых зерен металла (при этом на поверхности зерен могут появляться полосы скольжения) и накоплению сдвигов (которое на некоторых материалах проявляется в виде микроскопических бугорков и впадинок – экструзий и интрузий); затем происходит развитие сдвигов в микротрещины, их рост и слияние; на последнем этапе появляется одна или несколько макротрещин, которая достаточно интенсивно развивается (растет). Края трещины под действием переменной нагрузки притираются друг об друга, и поэтому зона роста трещины отличается гладкой (полированной) поверхностью. По мере роста трещины поперечное сечение детали все больше ослабляется, и, наконец, происходит внезапное хрупкое разрушение детали, при этом зона хрупкого долома имеет грубозернистую кристаллическую структуру (как при хрупком разрушении).

Из фотографии (рис.15.3) видно, что разрушение бруса произошло в результате развития трещины, образовавшейся у края сечения. Разрушение рельса (рис.15.4) обусловлено развитием трещины, образовавшейся внутри сечения в зоне местного порока.

Теоретический анализ усталостной прочности связан с большими трудностями. Природа усталостного разрушения обусловлена особенностями молекулярного и кристаллического строения вещества. Поэтому схема сплошной среды, которая с успехом применялась в рассматривавшихся до сих пор задачах, в данном случае не может быть принята в качестве основы для исследования.

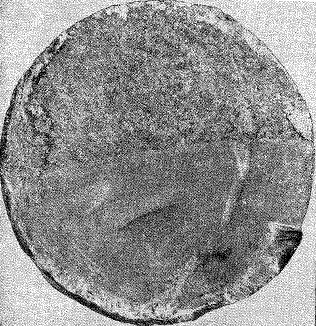
Рис.15.3

Рис.15.4

Для создания достаточно стройной теории усталостной прочности необходимо проникнуть в особенности строения кристаллов и межкристаллических связей с последующим привлечением аппарата статистики.

В настоящее время, однако, физические основы теории твердого тела не находятся еще на такой стадии развития, чтобы на их базе можно было бы создать методы расчета на усталостную прочность, удовлетворяющие запросам практики. Поэтому приходится идти по пути накопления экспериментальных фактов, из совокупности которых можно было бы выбрать подходящие правила как руководство для расчета. Объединение и систематика экспериментальных данных и представляет собой в настоящее время содержание теории усталостной прочности.

Отсутствие единых основополагающих законов в этой теории лишает ее стройности. В результате полученные экспериментальные зависимости не являются универсальными, а сами расчеты дают сравнительно невысокую точность.

Основные характеристики цикла и предел усталости

Рассмотрим вначале случай одноосного напряженного состояния.

Закон изменения главного напряжения о во времени представлен кривой, показанной на рис.15.5.

Наибольшее и наименьшее напряжения цикла обозначим через и . Их отношение называется коэффициентом цикла .

Рис.15.5

В случае, когда и цикл называется симметричным. Такой цикл, в частности, имеет место в рассмотренном выше примере вращающейся оси вагона). Если или же , цикл называется пульсационным (рис.15.6). Для пульсационного цикла r = 0 или . Циклы, имеющие одинаковые показатели r, называются подобными.

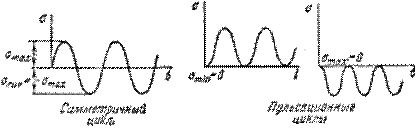
Рис.15.6

Любой цикл может быть представлен как результат наложения постоянного напряжения на напряжение, меняющееся по симметричному циклу с амплитудой (рис.15.6). Очевидно, при этом:

Тогда, в общем случае, цикл может быть представлен как сумма и напряжения, меняющегося по симметричному циклу с амплитудой , т.е.

Считается общепризнанным, что усталостная прочность детали не зависит от закона изменения напряжений внутри интервала . Поэтому между циклами, показанными, например, на рис.15.7, различия не делается. Точно также считается несущественным и влияние частоты изменения цикла. В итоге цикл определяется только величинами и или же и .

Рис.15.7

Теперь перейдем к механическим характеристикам материала. В условиях циклических напряжений они определяются путем специальных испытаний.

Наиболее распространенными являются испытания в условиях симметричного цикла. При этом обычно используется принцип чистого изгиба вращающегося образца (рис.15.8).

Рис.15.8

Для испытаний в условиях несимметричных циклов используются либо специальные машины, либо же вводятся дополнительные приспособления. Так, например, можно на испытуемом образце установить пружину, создающую постоянное растяжение образца с напряжением . Во время испытания на это напряжение накладывается напряжение от изгиба, меняющееся по симметричному циклу.

Путем многократных испытаний (если имеется достаточное количество образцов) можно определить число циклов, которое выдерживает образец до разрушения, в зависимости от величины цикла. Эта зависимость имеет вид кривой, показанной на рис.15.9 и называется диаграммой усталостного разрушения Велера.

Рис.15.9

В связи с тем, что число циклов с уменьшением возрастает в высокой степени, предпочитают в ряде случаев по оси абсцисс откладывать не число N, а его логарифм.

Опыт показывает, что для большинства черных металлов можно указать такое наибольшее максимальное напряжение, при котором материал не разрушается при любом числе циклов. Такое напряжение называется пределом усталости, или пределом выносливости.

Предел выносливости обозначается через , где индекс r соответствует коэффициенту цикла. Так, для симметричного цикла обозначение предела выносливости принимает вид , для пульсирующего или и т. д.

Для цветных металлов и для закаленных до высокой твердости сталей не удается установить такое число циклов, выдержав которое, образец не разрушился бы в дальнейшем. Поэтому в подобных случаях вводится понятие условного предела выносливости. За условный предел выносливости принимается напряжение, при котором образец способен выдержать 10⁸ циклов.

Определение предела выносливости является трудоемкой операцией, поэтому был сделан ряд попыток связать эмпирическими формулами предел выносливости с известными механическими характеристиками материала.

Обычно считается, что для сталей предел выносливости при изгибе составляет половину от предела прочности:

Для высокопрочных сталей можно принять:

Для цветных металлов предел выносливости изменяется в более широких пределах:

Аналогично испытанию на чистый изгиб можно вести испытание на кручение в условиях циклически изменяющихся напряжений. В этом случае:

или для обычных сталей берется , для хрупких материалов (высоколегированная сталь, чугун) .

Указанные соотношения и все им подобные следует, однако, применять с большой осторожностью, поскольку они получены только для определенных материалов и в определенных условиях испытаний (при изгибе, при кручении).

В связи с этим следует указать, что предел усталости не является характеристикой только свойств материала, как, например, модуль упругости или коэффициент Пуассона. Он зависит также от метода ведения испытаний. Расчетное напряжение для образца не определяет полностью процесс усталостного разрушения. В результате образования трещины величина напряжений и законы их распределения в образце непрерывно меняются в зависимости от условий дальнейшего развития трещины. Последние же в свою очередь зависят от абсолютных размеров образца и характера приложения внешних сил. Все это неминуемо сказывается на предельном числе циклов и на величине предела усталости.

В результате указанных обстоятельств, например, предел усталости, полученный в условиях циклического растяжения и сжатия, оказывается на 10-20% ниже, чем предел усталости, полученный при изгибе. Предел усталости при кручении сплошных образцов отличается от предела усталости, полученного для полых образцов, и т. п.

Диаграмма усталостной прочности

Положим, имеется машина, на которой можно производить усталостные испытания в условиях любого несимметричного цикла. Задавая постоянное значение , находим путем последовательных испытаний образцов такое наибольшее значение амплитуды , при котором материал способен еще выдержать неограниченное число циклов. Если для взятого материала такого предельного напряжения не существует, величина определяется по условному базовому числу N.

В результате проведенной серии испытаний устанавливается предельное значение , соответствующее некоторому напряжению . Полученный результат может быть графически изображен точкой в системе координат , ( рис.15.10). Сумма координат этой точки дает предельное максимальное напряжение цикла, т. е. предел усталости , где:

Продолжая такие испытания и дальше, получаем множество точек, через которые проводится предельная кривая, характеризующая прочностные свойства материала в условиях несимметричных циклов. Эта кривая носит название диаграммы усталостной прочности (рис.15.11).

Точки А и С диаграммы соответствуют пределам прочности при простом растяжении и сжатии. Точка В отражает результаты испытания в условиях симметричного цикла.

Полученная диаграмма дает возможность судить о прочности конструкции, работающей при циклически изменяющихся напряжениях.

Положим, для некоторой детали цикл характеризуется значениями напряжений и . Эти величины могут рассматриваться как координаты рабочей точки в плоскости , . Если рабочая точка располагается ниже предельной кривой, рассматриваемая деталь может в условиях циклически изменяющихся напряжений работать неограниченно долго. Если рабочая точка оказывается выше предельной кривой, деталь разрушится после некоторого числа циклов.

Так как построение диаграммы усталостной прочности связано с весьма трудоемкими испытаниями, предпочитают обычно полученную кривую АВС заменять двумя прямыми АВ и ВС, как это отмечено пунктиром на рис.15.11. Рабочая область при этом несколько сокращается, что дает погрешность в запас прочности.

Рис.15.10. Реализация предельного напряжения.

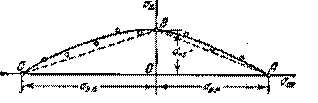
Рис.15.11. Диаграмма усталостной прочности.

Одновременно отсекается сомнительная зона разброса экспериментальных точек.

Для построения упрощенной диаграммы достаточно располагать пределом усталости при симметричном цикле , и иметь значения пределов прочности и .

Рабочая точка в плоскости , не может занимать произвольное положение. Она должна находиться в области осуществимых циклов, которая определяется следующими очевидными условиями:

Так как:

то область осуществимых циклов имеет верхнюю границу в виде двух прямых:

Эти прямые вместе образуют треугольник АСD (рис.15.12), который и представляет собой область осуществимых циклов.

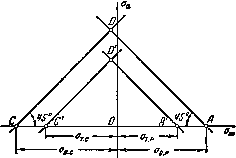
Рис.15.12. Область осуществимых циклов

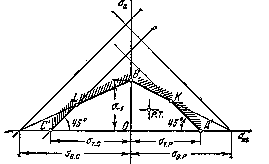
Рис.15.13. Область допустимых циклов с ограничениями

на пластические деформации.

Для пластичных материалов таким же способом может быть отмечена область упругих деформаций. Граница этой области очерчивается сверху прямыми:

В результате получаем треугольник (рис.15.12).

Если рабочая точка оказывается в пределах этого треугольника» пластические деформации в детали не возникают. Рабочая точка, находящаяся за пределами треугольника , но остающаяся внутри треугольника АСD, свидетельствует о том, что в детали возникают пластические деформации. Если, наконец, рабочая точка оказывается за пределами треугольника АСD, при первом же цикле происходит разрушение детали.

При расчетах конструкций, предназначенных на длительные сроки службы, напряжения цикла ограничиваются как по условиям усталостной прочности, так и по условиям недопущения пластических деформаций. Поэтому, объединяя диаграммы, показанные на рис.15.11 и 15.12, получаем рабочую область в виде многоугольника (рис.15.13). Рабочая точка (р.т.) исследуемого цикла для рассчитываемой детали должна находиться в пределах указанного многоугольника.

Теперь возникает вопрос, как определить координаты рабочей точки и как определить коэффициент запаса детали в условиях циклического нагружения. Оба эти вопроса содержат в своем решении ряд специфических особенностей, к рассмотрению которых сейчас и перейдем.

Расчет коэффициентов запаса усталостной прочности

Одним из основных факторов, которые необходимо учитывать при практических расчетах на усталостную прочность, является фактор местных напряжений.

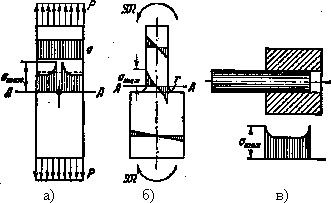
Рис.15.14. Очаги концентрации местных напряжений:

а) растяжение, б) изгиб, в) контактные напряжения

Многочисленные теоретические и экспериментальные исследования показывают, что в области резких изменений в форме упругого тела (входящие углы, отверстия, выточки), а также в зоне контакта деталей возникают повышенные напряжения с ограниченной зоной распространения, так называемые местные напряжения.

Например, при растяжении полосы с небольшим отверстием (рис.15.14, а) закон равномерного распределения напряжений вблизи отверстия нарушается. Напряженное состояние становится двухосным, а у края отверстия появляется пик напряжения. Аналогично при изгибе ступенчатого стержня (рис.15.14, б) в зоне входящего угла возникает повышенное напряжение, величина которого зависит в первую очередь от радиуса закругления r. При прессовой посадке втулки на вал (рис.15.14, в) у концов втулки и вала также возникают местные напряжения. Подобных примеров можно привести очень много.

Величина местных напряжений в зависимости от геометрической формы детали определяется обычно теоретически при помощи методов математической теории упругости.

Основным показателем местных напряжений является теоретический коэффициент концентрации напряжений:

где — наибольшее местное напряжение, а — так называемое номинальное напряжение. Это - то напряжение, которое определяется по формулам сопротивления материалов без учета эффекта концентрации. Обычно подсчет ведется по наиболее ослабленному сечению детали, как, например, по сечению АА (рис.15.15).

Рис.15.15. Зона расчета номинального напряжения

Например, для полосы с отверстием (рис.15.14, а)

для случая изгиба ступенчатого стержня (рис.15.14, б)

Однако, если при подобных подсчетах возникают трудности, за номинальное принимается напряжение в неослабленном сечении. Например, при кручении вала, имеющего поперечное отверстие (рис.15.15), имеем:

где — полярный момент сопротивления неослабленного сечения.

Так или иначе, номинальное напряжение выбирается в первую очередь из соображений, связанных с простотой расчета.

Величина теоретического коэффициента концентрации определена для большинства встречающихся на практике типовых конструктивных элементов.

Данные по величине приводятся в виде таблиц; в справочной литературе по машиностроению. Так, например, на рис.15.16 показана зависимость теоретического коэффициента концентрации от соотношения геометрических размеров полосы с отверстием.

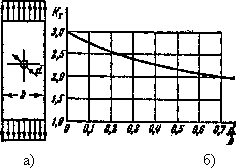
Рис.15.16. Определение коэффициента концентрации для полосы

с отверстием — а), с использованием графика — б)

Наличие местных напряжений оказывает на прочность детали различное влияние в зависимости от свойств материала и от характера нагружения. В связи с этим в отличие от теоретического вводится понятие эффективного коэффициента концентрации , причем делается различие между постоянными и циклически изменяющимися напряжениями.

При постоянных напряжениях (при r = 1) под эффективным коэффициентом концентрации понимается отношение

где — предел прочности для образца, не имеющего очагов концентрации, а —условный предел прочности для образца, обладающего очагами концентрации напряжений.

При испытании, например, призматического стержня с отверстием (рис.15.17, а) эффективный коэффициент концентрации напряжений вблизи отверстия определяется отношением разрушающей нагрузки Р к разрушающей нагрузке Р'. То же самое имеет место и для образца с выточкой (рис.15.17, б).

Для пластичных материалов местные напряжения в условиях постоянной нагрузки не оказывают на прочность детали существенного влияния. Обычно в зоне повышенных напряжений образуются местные пластические деформации без образования трещины, Весь остальной объем тела за пределами этой зоны работает упруго, и несущая способность сохраняется практически до тех же значений сил, что и при отсутствии очагов концентрации. Это дает право при статическом нагружении не учитывать местных напряжений.

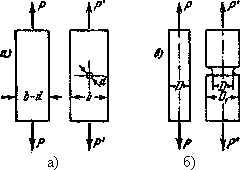
Рис.15.17. Эффект концентрации местных напряжений для детали

с отверстием — а) и с выточкой — б)

Таким образом, можно считать, что для пластичных материалов: .

Для хрупких материалов значение приближается к значению теоретического коэффициента концентрации . Здесь, правда, возможны исключения. Для чугуна, например, независимо от формы детали, . Объясняется это структурными особенностями чугуна, имеющего в своей массе включения графита. Каждое включение является очагом концентрации, приводящим к существенно большим местным напряжениям, чем те, которые обусловливаются конструктивными факторами (выточками, отверстиями и пр.).

В условиях циклически изменяющихся напряжений (при k = -1) эффективный коэффициент концентрации определяется отношением:

где — предел усталости гладкого образца, а — предел усталости образца, имеющего очаги концентрации напряжений.

Величина , также как и зависит не только от геометрической формы детали, но и от механических свойств материала. Концентрация напряжений существенно сказывается на усталостной прочности и хрупких и пластичных материалов, поскольку и в том и в другом случае при многократном изменении напряжений разрушение начинается с образования местной трещины.

   Числовое значение эффективного коэффициента концентрации может быть определено только на основе усталостного испытания большого числа образцов из различных материалов. В настоящее время в этом направлении накоплен достаточно большой экспериментальный материал. Сопоставление полученных результатов позволяет в некоторой ограниченной мере установить соотношение между эффективным и теоретическим коэффициентами концентрации в виде

где q — так называемый коэффициент чувствительности материала к местным напряжениям.

Величина q зависит в основном от свойств материала. Так, например, можно считать, что для высокопрочных легированных сталей величина q близка к единице. Для конструкционных сталей в среднем , причем более прочным сталям соответствуют большие значения q. Для чугуна q = 0 и .

Коэффициент чувствительности зависит также в некоторой степени и от геометрических особенностей очага концентрации. Наблюдается некоторое снижение q в случае больших коэффициентов .

При расчетах на усталостную прочность наличие местных напряжений учитывается путем введения поправок в числовые значения координат рабочей точки (р.т.) на диаграмме усталостной прочности. Так, если расчет детали по номинальным напряжениям дает характеристики цикла и , то с учетом местных напряжений следует соответственно принять значения координат рабочей точки в виде и , где принимается обычно равным единице.

Из всего изложенного следует, что наличие концентрации напряжений снижает усталостную прочность детали. Поэтому при проектировании машин следует стремиться к тому, чтобы влияние местных напряжений было сведено к минимуму. Достигается это, прежде всего, конструктивными мерами. Для ответственных деталей, работающих в условиях циклических напряжений, внешние обводы стремятся сделать возможно более плавными, радиусы закругления во внутренних углах увеличивают, необходимые отверстия располагают в зоне пониженных напряжений и т. д.

Рис.15.18

На рис.15.18, а показана конструкция галтели с глубоким поднутрением, уменьшающим местные напряжения. Для увеличения радиуса галтели могут применяться также проставочные кольца, как это показано на рис.15.18, б. Для снижения местных напряжений иногда практикуется введение разгрузочных канавок (рис.15.19,а), наличие которых благотворно сказывается на усталостной прочности вала. Такого же рода разгрузочные канавки могут применяться и в местах посадки (рис.15.19, б).

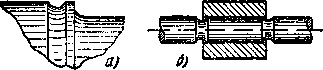
Рис.15.19

Влияние состояния поверхности и размеров детали на усталостную прочность

Так как при циклических напряжениях начало разрушения связано с образованием местной трещины, понятна та роль, которую играет в усталостной прочности детали состояние ее поверхности. Совершенно очевидно, что в случае чистой и тонко обработанной поверхности предел усталости возрастает. При грубой обработке наличие мелких поверхностных дефектов приводит к снижению показателей усталостной прочности. При этом для материалов, обладающих большой чувствительностью к местным напряжениям, влияние состояния поверхности будет более заметным.

При расчетах на усталостную прочность особенности, связанные с обработкой поверхности детали, учитываются коэффициентом качества поверхности:

где — предел усталости, полученный на образцах, имеющих стандартную обработку поверхности. В качестве таковой — принимается обычно шлифовка. предел выносливости для образцов, состояние поверхности которых соответствует состоянию поверхности рассчитываемой детали.

На графиках рис.15.20 приведены ориентировочные значения коэффициента качества поверхности различных сталей в зависимости от их предела прочности.

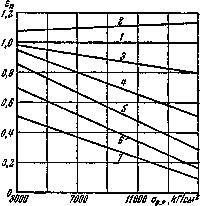
Рис.15.20. График определения коэффициента качества состояния поверхности

Предел прочности для шлифованных образцов принят за единицу (прямая 1). Прямая 2 относится к образцам с полированной поверхностью. Прямая 3 — к образцам, имеющим поверхность, обработанную резцом. Прямая 4 дает значения коэффициента качества поверхности, имеющей мелкую насечку, а 5 — относится к поверхности, необработанной после проката. Для поверхностей, корродированных в пресной и морской воде, значения , задаются прямыми 6 и 7.

Коэффициент качества поверхности вводится при расчетах в ординату рабочей точки (р.т.) на диаграмме усталостной прочности. Так, если рассчитанная по номиналу амплитуда цикла равна , то после введения поправки на качество поверхности она принимает значение . Абсцисса рабочей точки остается при этом неизменной, поскольку при постоянных напряжениях качество поверхности на прочность детали влияния не оказывает.

Из всего сказанного видно, что для повышения усталостной прочности необходимо добиваться высокой чистоты поверхности, особенно вблизи очагов концентрации напряжений. Ответственные детали, работающие в тяжелых условиях циклически изменяющихся напряжений, обычно шлифуются и даже полируются.

Большие возможности для повышения усталостной прочности открывают специальные способы обработки поверхности. Сюда относится поверхностное азотирование, которое дает особо ощутимые результаты при наличии концентрации напряжений Предел усталости может быть повышен также путем обкатки поверхности роликами.

Особенно большой эффект при наличии очагов концентрации дает дробеструйная обработка поверхности, заключающаяся в обдувке детали чугунной или стальной дробью. В результате такой обработки образуется поверхностный слой с остаточными напряжениями сжатия, что препятствует возникновению местных трещин в дальнейшем.

При расчете детали на усталостную прочность наряду с фактором состояния поверхности необходимо учитывать также еще так называемый масштабный фактор.

Величина предела усталости зависит от абсолютных размеров испытываемых образцов. Объясняется это, как уже указывалось выше, тем, что усталостное разрушение определяется не только напряжением в наиболее опасных точках, но также и общими законами распределения напряжений в объеме тела в процессе образования и развития трещин.

Опыты, проведенные по определению предела усталости для образцов различных размеров, показали, что с увеличением последних предел усталости уменьшается.

Отношение предела усталости детали к пределу усталости образцов стандартного размера мм называется коэффициентом масштабного фактора, или просто масштабным фактором,

При определении масштабного фактора предполагается, что состояние поверхности испытываемых деталей и образцов одинаково.

На рис.15.21 дается ориентировочная зависимость масштабного фактора от диаметра вала для случая изгиба и кручения.

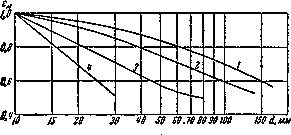
Рис.15.21. График определения масштабного коэффициента

Кривая 1 получена для углеродистой стали при отсутствии местных напряжений. Кривая 2—для легированной стали кг/см² при отсутствии концентрации напряжении и для углеродистой стали при умеренной концентрации. Кривая 3 относится к легированной стали при наличии концентрации напряжений, а 4 — к сталям, имеющим высокую степень концентрации напряжений. Как видно из этих кривых, масштабный фактор более резко сказывается при больших местных напряжениях.

При расчетах на прочность коэффициент , так же как и , вводится только в ординату рабочей точки; вместо номинального значения амплитуды цикла берется значение .

Коэффициент запаса усталостной прочности и его определение

Построим диаграмму усталостной прочности и нанесем на ней рабочую точку цикла. Диаграмма строится, как это было показано выше, на основе заданных механических характеристик материала и , а рабочая точка определяется по номинальным значениям напряжений цикла и . С учетом поправки на концентрацию напряжений, на поверхностный и масштабный факторы координаты рабочей точки примут значения и (рис.15.22).

Условимся под запасом усталостной прочности понимать отношение отрезка ОВ к отрезку ОА (см. рис.15.22)

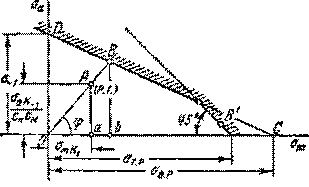
Рис.15.22. Диаграмма усталостной прочности.

Это отношение характеризует степень близости рабочих условий к предельным для данного материала. В частном случае, когда напряжения не меняются во времени (), данное определение запаса прочности совпадает с обычным.

При подсчете запаса прочности можно прибегать к графическому построению диаграммы усталостной прочности и глазомерной оценке соотношения между отрезками. Точность такого определения остается в пределах точности определения исходных величин и последующих поправок.

В большинстве случаев для определения n предпочитают пользоваться расчетными формулами. Они получаются из геометрических соотношений отрезков, показанных на рис.15.22.

Уравнения прямых СD и ОB будут:

Исключая из этих уравнений , находим абсциссу точки B, т.е. - отрезок Оb,

Искомый запас усталостной прочности:

Так как:

то

Если точка В находится на прямой, ограничивающей цикл по пределу текучести (точка В' на диаграмме рис.15.22), расчет на усталостную прочность заменяется обычным расчетом по пределу текучести.

Все рассмотренные до сих пор вопросы усталостной прочности относились к случаю одноосного напряженного состояния. Аналогичным образом могут быть получены соотношения усталостной прочности и при чистом сдвиге (кручении). Эксперименты показывают, что диаграмма усталостной прочности для сдвига заметно отличается от прямой линии, свойственной простому растяжению-сжатию, и имеет вид кривой. В первом приближении эту кривую в координатных осях , можно представить в виде двух наклонных, как это изображено на рис. 15.23. Причем, если одна из них (ближняя к оси ординат) соответствует разрушению образца вследствие усталостных явлений, то другая - по причине наступления пластического состояния.

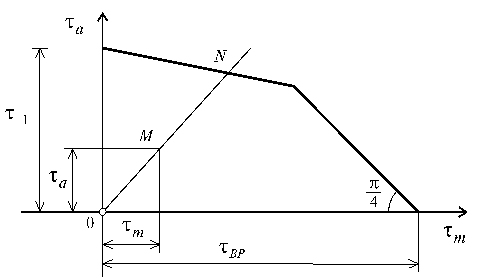
Рис. 15.23

В данном случае расчетная формула для записывается в виде

где - эмпирическая величина, определенная на основе обработки экспериментальных данных, .

В случаях более общего напряженного состояния задача существенно усложняется.

Известны многие попытки создания гипотез усталостной прочности в сложном напряженном состоянии. Все они сводились в основном к обобщению известных гипотез предельных состояний на случай циклических напряжений. Такой путь, однако, до сих пор не дал положительных результатов, и в настоящее время приходится пользоваться в основном экспериментально установленными зависимостями.

Для наиболее часто встречающегося на практике расчета при двухосном напряженном состоянии , общепринятой в настоящее время является эмпирическая формула Гафа и Полларда

где n — искомый запас усталостной прочности; — запас усталостной прочности в предположении, что касательные напряжения отсутствуют; — запас по касательным напряжениям, установленный в предположении, что .

Приведенная формула применима не только в случае синфазного изменения и но и при таких циклах, когда максимумы и достигаются не одновременно.

Резюмируя заметим, что в настоящее время в связи с тем, что физические основы теории твердого деформируемого тела недостаточно развиты, многие предпосылки современной теории усталостной прочности базируются на эмпирической основе. Отсутствие твердых предпосылок в теории выносливости, в современном виде лишает ее нужной строгости. Так как полученные эмпирические зависимости не являются универсальными, сами результаты расчетов являются достаточно приближенными. Однако указанные приближения оказываются допустимыми для решения инженерных задач.

Колебания системы с одной степенью свободы

Упругими колебаниями называют движения упругих тел, представляющие собой периодические отклонения их относительно положения равновесия.

При исследовании колебаний упругих систем различают собственные (свободные) и вынужденные колебания. Под собственными колебаниями понимается движение системы при отсутствии внешних воздействий. Если колебание системы сопровождается действием внешних сил, то движение называется вынужденным.

В динамических расчетах важным понятием является число степеней свободы системы – наименьшее количество независимых геометрических параметров, определяющих положение всех масс системы в произвольный момент времени. Системами с одной степенью свободы будут такие, у которых для полной фиксации их геометрического состояния в любой момент времени достаточно знать один параметр, например, положение определенной точки. Таковы, например, растянутая или сжатая незначительного веса пружина с грузом на конце, совершающая продольные колебания; небольшого (сравнительно с грузом Q) собственного веса балка, изображенная на рис.15.24, колеблющаяся в направлении, перпендикулярном к ее оси, и т. п.

Рис.15.24

Простейшим видом колебаний являются гармонические колебания, которые описываются тригонометрическими функциями синуса или косинуса, например,

где А₀ – амплитуда, т.е. максимальное значение обобщенной координаты x при колебаниях системы (рис. 15.25); – круговая частота свободных колебаний; – фаза колебаний; – начальная фаза колебаний, т.е. фаза в момент времени t = 0.

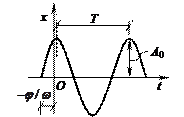
Рис.15.25

Промежуток времени за который совершается полный цикл колебаний, носит название периода собственных или вынужденных колебаний, смотря по тому, о каких колебаниях идет речь. Период колебаний обозначается через Т. Величина обратная Т, называется частотой колебаний:

V=1/T,

и представляет собой число колебаний в течение одной секунды. В технике в большинстве случаев используется понятие круговой частоты , представляющей собой число колебаний за секунд.

Период колебаний и круговая частота свободных колебаний связаны зависимостью

Круговая частота связана с сосредоточенной массой m и жесткостью с системы зависимостью

Жесткость системы – это сила, которая вызывает перемещение, равное единице. Часто масса колеблющейся системы считается постоянной, а упругая система линейной, для которой сила упругости Р = mg (g – ускорение свободного падения) пропорциональна соответствующему перемещению , т. е.

Учитывая приведенные выше соотношения, можно записать формулы для круговой частоты и периода свободных колебаний, каждая из которых в том или ином случае может оказаться удобной при решении практических задач:

Возможны системы с несколькими упругими связями, каждая из которых имеет свою жесткость. На рис. 15.26, а показана схема механической системы с так называемым параллельным соединением упругих связей с жесткостями и , а на рис. 15.26, б – с последовательным соединением упругих связей. Суммарные жесткости показанных систем рассчитываются по-разному.

Рис.15.26

При параллельном соединении упругих связей жесткость системы рассчитывается по формуле

а при последовательном соединении

В предыдущих формулах под массой m понимается масса груза, совершающего колебания, без учета собственной массы системы. В остальных задачах принято, что масса m состоит из массы груза, совершающего колебания, и приведенной к точке распределенной собственной массы системы

где – истинная собственная масса системы; – коэффициент привидения. Принимаем подобно коэффициенту приведения при ударной нагрузке – при продольных колебаниях систем, типа показанной на рис. 15.27, а; – для изгибных колебаний шарнирно опертой балки на двух опорах (рис. 15.27, б); – для изгибных колебаний консоли (рис. 15.27, в).

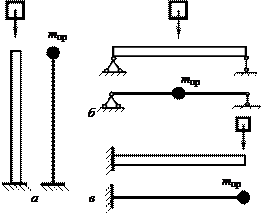
Рис.15.27

Определение напряжений при колебаниях. Резонанс

Колебания происходят около положения упругого равновесия, при котором в нагруженной системе имели место статические деформации и соответствующие им статические напряжения ( или — в зависимости от вида деформации). При колебаниях к статическим деформациям добавляются динамические, зависящие от вида колебательного движения и от величины размаха (амплитуды) колебаний. В связи с этим изменяются и напряжения . Таким образом, при расчете колеблющейся системы на прочность необходимо уметь вычислять динамические добавки к статическим деформациям и соответствующим им напряжениям.

При колебаниях систем с одною степенью свободы полные деформации системы в каком либо сечении могут быть найдены путем сложения статической деформации с добавочной деформацией при колебаниях. Для проверки прочности системы, очевидно, необходимо найти наиболее опасное сечение с наибольшей в процессе колебаний суммарной величиной деформации. В простейших случаях для этого потребуется сложить наибольшую статическую деформацию с наибольшей амплитудой колебаний А, т. е.

Пока система деформируется в пределах упругости, напряжения пропорциональны деформациям. Поэтому

где — коэффициент динамичности при колебаниях. Условие прочности в этом случае должно иметь такой вид:

Таким образом задача нахождения динамических напряжений и проверки прочности при колебаниях может быть сведена к определению статических напряжений и коэффициента динамичности . Так как последний зависит от величины А, то нужно уметь определять наибольшее значение амплитуды колебаний в разных случаях.

Как известно, дифференциальное уравнение движения колеблющегося груза Q в случае свободных колебаний можно представить в виде уравнения равновесия, в котором кроме внешней силы (веса груза Q) и силы упругого сопротивления системы учитывается также и сила инерции:

Здесь x — координата, полностью определяющая положение груза Q во время колебаний; Р — полное упругое сопротивление системы при колебаниях; P-Q=P₁ — так называемая восстанавливающая сила (добавочное упругое усилие, возникающее в системе в результате перемещения точки приложения груза Q на расстояние x при колебаниях), которую в пределах упругости можно считать пропорциональной координате x (P₁=cx); с — коэффициент пропорциональности, представляющий собой усилие, необходимое для того, чтобы вызвать равную единице статическую деформацию системы в направлении действия груза Q. Если статическая деформация от груза Q равна , то .

Решение уравнения приводит к таким формулам для вычисления частоты и периода свободных колебаний:

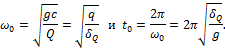
Свободные колебания невесомого тела суть простые гармонические колебания с частотой (периодом), равной частоте (периоду) колебаний математического маятника, длина которого равна статической деформации системы от груза Q. Так, например, если груз Q растягивает призматический стержень,

при изгибе балки на двух шарнирных опорах грузом Q посредине пролета

Если на упругую систему, кроме груза Q и силы упругого сопротивления системы Р, в том же направлении действует периодически меняющаяся возмущающая сила S и сила сопротивления среды R, то дифференциальное уравнение движения груза Q при колебаниях также может быть представлено в виде уравнения равновесия, подобного уравнению (15.13):

Силу сопротивления среды R на практике в довольно большом числе случаев можно считать пропорциональной первой степени скорости колебательного движения, т. е. . Если возмущающая сила S меняется по синусоидальному закону:

,

где , а — частота возмущающей силы, то уравнение (15.14) может быть переписано так:

или

Здесь — так называемый коэффициент затухания колебаний, a — найденная выше частота свободных колебаний системы, возникающих при отсутствии как возмущающей силы S так и силы сопротивления R.

Решение уравнения (15.15) приводит к такому выражению для амплитуды А вынужденных колебаний при наличии сил сопротивления:

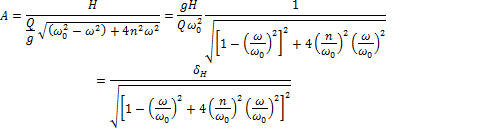
Здесь — статическая деформация системы от наибольшей величины возмущающей силы S (). Отношение амплитуды вынужденных колебаний А к величине деформации называется коэффициентом нарастания колебаний :

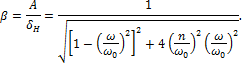
Таким образом, для динамического коэффициента получает теперь такой вид:

В этом выражении не учтена амплитуда собственных колебаний системы, которая может иметь сколько-нибудь существенное значение лишь в самом начале процесса колебаний; при наличии сил сопротивления она довольно быстро уменьшается с течением времени.

На рис.15.28 приведены графики изменения коэффициента нарастания колебаний в зависимости от величины отношения при разных значениях коэффициента затухания колебаний n (отношения ). Если частота изменения возмущающей силы близка к частоте свободных колебаний системы, т.е. , и если величина коэффициента затухания колебаний сравнительно невелика, то знаменатели формул и для A и будут очень малыми, амплитуда колебаний и коэффициент нарастания колебаний будут очень большими. В этом случае даже небольшая возмущающая сила может вызвать высокие напряжения (явление резонанса). При резонансе амплитуда (размах) колебаний будет резко расти с течением времени. Наличие сил трения, сопротивление воздуха и т. д. ограничивают на практике рост этой амплитуды; однако она может достичь очень большой величины, значительно превышающей те деформации, которые испытывала бы конструкция под действием ускорений той же величины, но не меняющих знака.

Известен случай, когда при резонансе угол закручивания вала увеличился в шесть раз по сравнению с тем углом, который был до наступления резонанса, — это был случай поломки коленчатых валов двигателей «Цеппелина» при первом его перелете через Атлантический океан.

Таким образом, явление резонанса, если оно длится некоторое время, а не сбивается немедленно по возникновении, ведет к постепенному росту деформаций и пропорциональных им напряжений в конструкции, что может вызвать поломку. Поэтому, как правило, при проектировании конструкций, испытывающих переменные ускорения с постоянным периодом, необходимо избежать возникновения явления резонанса.

Так как период раскачивающих (возмущающих) сил обычно является заданным, то в распоряжении проектировщика остается лишь период собственных свободных колебаний конструкции, который надо подобрать так, чтобы он в должной мере отличался от периода изменений возмущающей силы.

Рис.15.28

С увеличением сил сопротивления явление резонанса становится все менее заметным. Заметим, однако, что силы сопротивления значительно уменьшают величину амплитуды вынужденных колебаний только вблизи от резонанса ; при других величинах отношения — влияние сил сопротивления незначительно.

Из рис.15.28 видно, что если частота изменения возмущающей силы S очень мала, то амплитуда колебаний приближается к величине , коэффициент нарастания колебаний стремится к единице и наибольшие напряжения в системе могут быть вычислены как статические напряжения от груза Q и наибольшего значения возмущающей силы S. При очень большой частоте изменения возмущающей силы S амплитуда колебаний и коэффициент нарастания колебаний стремятся к нулю, груз Q можно рассматривать как неподвижный; поэтому наибольшее напряжение в системе равно статическому напряжению от груза Q.

Это обстоятельство имеет очень большое практическое значение; оно используется при конструировании разного рода поглотителей колебаний, сейсмографов, вибрографов и других приборов. В машиностроении амортизаторы, предохраняющие основания машин от усилий, возникающих при колебаниях, подбираются так, чтобы частота собственных колебаний машины на амортизаторах была значительно меньше частоты изменения возмущающей силы.

Колебания балки с установленным на ней массивным электромотором

Пример 1.

Рассмотрим шарнирно опертую балку с пролетом l с постоянным поперечным сечением с установленной на ней электромотором весом Q с неуравновешенной массой m_e и эксцентриситетом e. Число оборотов электромотора n об/мин. Будем исследовать напряженно-деформированное состояние в двух случаях: 1) правая опора абсолютно жесткая; 2) правая опора упругая.

Сначала рассмотрим первый случай.

Считаем, что масса электромотора значительно больше всей массы балки. Это позволяет упростить задачу, и пренебречь массой балки по сравнению с массой M электромотора, которую условно считаем приложенной в точке оси балки на расстоянии а от левой опоры (рис. 15.29, а). Для выяснения характера воздействия на балку вращающихся неуравновешенных частей рассмотрим рис. 15.30.

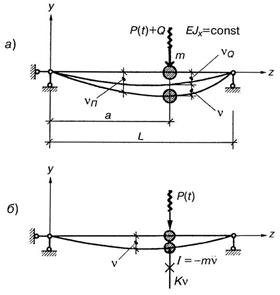
Рис. 15.29

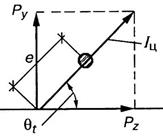
Рис. 15.30

На балку со стороны вращающейся массы m_e действует центробежная сила

где V – линейная скорость массы окружности радиуса е. Вычисляем угловую скорость вращения ротора по формуле

и линейную скорость

вместо (15.16), получим

Выразив массу через вес , вместо (15.19) получим

Разложим эту силу на составляющие по осям Y и Z.

Сила вызывает изгиб балки, а продольная сила вызывает деформации растяжения-сжатия, которые в дальнейшем учитывать не будем.

Положение массы на плоскости YOY будет определяться одним параметром – прогибом , который можно считать суммой прогибов балки при статическом действии веса неработающего мотора и прогиба балки от действия вращающейся неуравновешенной массы -

Запишем, используя принцип Даламбера, динамическое равновесие массы m, на которую в произвольный момент времени действует сила инерции, сумма сил и упругая сила отпора балки при перемещении , равная - , где K - коэффициент жесткости балки в точке прикрепления мотора. Эта величина численно равна силе, приложенной к балке в этой точке и вызывающей прогиб равный единице. Можно приложить силу и определить от нее прогиб (рис. 15.31). Тогда

Итак

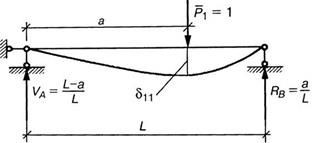
Рис. 15.31

Продифференцировав (15.23) дважды по времени, и учтя, что - прогиб не зависит от времени, получим

Теперь вместо (15.25), получим

Далее учтем, что по закону Гука

Поэтому вместо (15.26) будем рассматривать дифференциальное уравнение для динамической части прогиба (рис.15.29,б)

или

Обозначим

тогда получим дифференциальное уравнение динамического прогиба балки как системы с одной степенью свободы без учета сил сопротивления

Это дифференциальное уравнение линейное второго порядка с известной правой частью.

В математике доказывается, что решение такого уравнения ищется в виде суммы общего решения однородного дифференциального уравнения

и частного решения уравнения (15.32).

Однородное дифференциальное уравнение (15.33) описывает свободные или собственные колебания упругой системы с одной степенью свободы.

Свободные колебания вызываются начальными воздействиями. Например, можно медленно отодвинуть массу от положения равновесия и затем отпустить. При этом начальные условия будут иметь вид

Можно поступить иначе – толкнуть массу. При этом массе сообщается начальная скорость V₀ и начальные условия будут иметь вид

Известно, что решение уравнения (15.33) можно рассматривать в двух формах

или

В той и другой форме участвуют две постоянные интегрирования (А и В) или , которые можно определить из начальных условий (15.34) или (15.35) или их комбинаций.

Таким образом, собственные колебания (15.37) совершаются по закону синусоиды с амплитудой А₁ и круговой частотой

Известно, что функции в выражении (15.36) имеют общий период .

Отсюда,

Таким образом, круговая частота собственных колебаний есть число циклов колебаний за секунд.

Коэффициент А₁ характеризует размер колебаний и носит название амплитуды колебания, - начальная фаза колебаний.

Найдем частное решение (15.32), учтя, что функция имеет вид (15.21).

Обозначим амплитуду возмущающей силы

Ищем частные решения уравнения

в виде

Найдем производные по времени

и подставим (15.43), (15.44), (15.45) в (15.42)

откуда

Преобразуем

Учитывая (15.31), получим

где - величина прогиба балки от силы приложенной статическим образом.

Итак, частное решение (15.42) имеет вид

Таким образом, выражение динамического прогиба баки как системы с одной степенью свободы без учета сил сопротивления будет

В предыдущих рассуждениях мы не учли силы сопротивления, которые всегда возникают при колебаниях механических систем. Экспериментально доказано, что они вызывают затухание во времени собственных колебаний. Если все время действует вынуждающая сила, то изменение динамического прогиба при большом t описывается вторым слагаемым в (15.49), которое назовем вынужденным колебанием

Максимальный динамический прогиб будет при

Обозначив

как коэффициент нарастания колебаний, получим

Полный максимальный прогиб (15.23) (с учетом постоянно действующего веса электромотора) будет

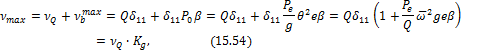
коэффициент динамичности. Он показывает во сколько раз полный максимальный прогиб больше прогиба балки от неработающего мотора.

В случае приближения частоты изменения вынуждающей силы к частоте собственных колебаний коэффициент нарастания колебаний стремится к бесконечности (если учесть силы сопротивления колебаниям, то он стремится к большой, но конечной величине). Такое явление называется резонансом. Нужно подбирать так, чтобы не допустить резонанса в проектируемой системе.

Итак, полный прогиб во времени (15.23) будет иметь вид

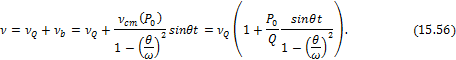
Определим максимальные напряжения при изгибе балки в точках наиболее удаленных от нейтральной оси в процессе колебаний

максимальное напряжение от неработающего мотора,

- изгибающий момент от единичной силы,

По (15.45) и (15.46)

Подставив (15.60) и (15.21) в (15.59), будем иметь

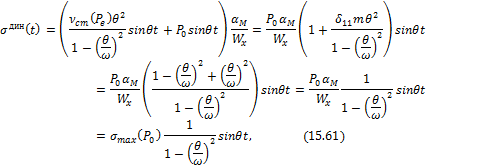
где - максимальное нормальное напряжение в наиболее удаленной точке сечения от амплитудного значения силы , приложенной статическим образом.

Итак (15.57) примет вид

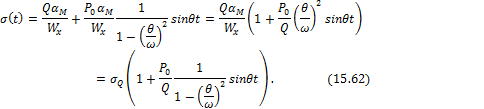
Максимальная величина достигается в момент соблюдения (15.51)

где - такой же коэффициент динамичности, который учитывается для прогиба (15.55).

Таким образом, для того чтобы определить максимальные по величине факторы, возникающие при колебаниях, нужно статические факторы умножить на коэффициент динамичности (см. формулы (15.54) и (15.63)).

Теперь рассмотрим второй случай опирания правого конца балки – упругое опирание, балка подвешена к растянутому стержню.

При этом изменится коэффициент жесткости K в месте прикрепления мотора. Теперь величина будет складываться из двух слагаемых: одно за счет прогиба балки на жестких опорах (как в первом случае) и перемещения балки как жесткого диска в том же сечении за счет опускания правого конца балки из-за деформации растянутого стержня (рис.15.32)

Таким образом,

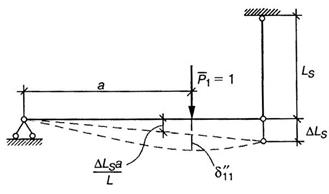
Рис.15.32

Введение упругой связи приводит к изменению собственной частоты системы с одной степенью свободы, изменению коэффициента нарастания колебаний и коэффициента динамичности. При сравнении двух случаев опирания все будет зависеть от того, в каком случае ближе будут частоты и , то есть ближе резонанс. Подрессоривание в случае колебаний не обязательно улучшает напряженно-деформированное состояние балки.

Пример 2.

Определить размеры поперечного сечения консольной балки с поперечным сечением, состоящим из двух швеллеров (рис. 15.33). На балке установлен электродвигатель, имеющий несбалансированную вращающуюся массу m. Произведение радиуса дисбаланса на массу mr=0,05 кгм. Длина балки l=1 м. Число оборотов массы n=3000 об/мин. Вес двигателя P=2000 Н. Коэффициент усиления колебаний при резонансе . Допускаемое напряжение материала балки = 60 МПа.

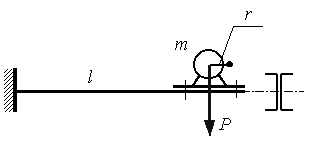
Рис. 15.33

Круговая частота возмущающей силы равна:

Частота собственных колебаний для консольной балки определяется по формуле:

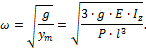
Условие прочности имеет следующий вид:

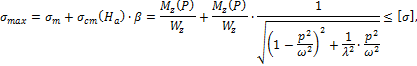
Максимальные изгибающие моменты действуют в заделке и равны соответственно:

где амплитудное значение возмущающей (инерционной) силы равно

Поскольку в условие прочности входят неизвестные моменты сопротивления и инерции, дальнейшие вычисления осуществляем методом последовательных приближений. Все расчеты для дорезонансной (первое приближение ) и зарезонансной (первое приближение ) областей сведены в таблицу 15.1.

Таблица 15.1.

	№ профиля	, см^4	Wz, см^3	, 1/сек	b	, МПа	, МПа	, МПа	, МПа
0.8	-	5241	-	392.7	-	-	-	-	-
0.76	24	5800	484	413.08	2.368	10.195	24.14	4.132	28.276
0.89	22	4220	384	352.35	4.832	12.851	62.096	5.208	67.304
0.848	22a	4660	424	370.26	3.554	11.639	41.368	4.717	46.085
1.2	-	2330	-	261.8	-	-	-
1.187	18a	2380	264	264.6	2.43	18.692	45.454	7.576	53.030
1.427	16a	1646	206	220	0.962	23.955	23.055	9.708	32.763
5.875	6.5	97.2	30	53.47	0.030	164.5	4.908	66.06	71.57
4.329	8	179	44.8	72.6	0.056	110.15	6.208	44.643	50.851

Как видно из таблицы 15.1, условию прочности отвечают для дорезонансной области швеллер номера 22а, а для зарезонансной области – швеллер номер 8. При этом вес погонного метра швеллера номера 22а в 3,2 раза больше, чем для швеллера номера 8. Кроме этого для швеллера номер 8 по сравнению с номером 22а, при примерно одинаковых максимальных напряжениях цикла, значительно меньше амплитуда напряжений цикла, что имеет существенное значение для усталостной прочности.

Степень свободы колеблющейся системы

Колебания упругих систем принято различать по числу степеней свободы n. Для упругой системы с геометрическими (голономными) связями под числом степеней свободы понимается число независимых координат, определяющих положение системы.

В случае кинематических (неголономных) связей число степеней свободы определяется числом независимых возможных перемещений.

На рис. 15.34 приведены примеры систем с сосредоточенными массами, степень свободы которых определяется по числу независимых перемещений , этих масс. В этих примерах мы пренебрегаем массой, распределённой в элементах самой системы.

Реальная система обладает бесконечным числом степеней свободы. Рассмотрим, например, балку на двух опорах (рис. 15.35). Ее можно разбить на любое число участков (в том числе и бесконечно малых dl). Массу каждого участка можно сосредоточить в его середине. В зависимости от числа полученных сосредоточенных масс и количества их независимых перемещении мы можем легко подсчитать степень свободы системы. В пределе, когда число участков стремится к бесконечности, приходим к системе с бесконечным числом степеней свободы. В изображенном на рис. 15.35 случае n = 4.

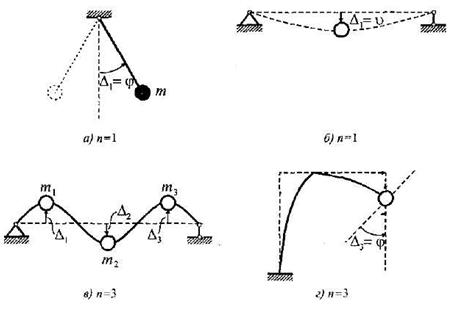
Рис. 15.34

а) б)

Рис. 15.35

Таким образом, число степеней свободы системы определяется фактически выбором ее расчетной схемы т.е. степенью приближения, к реальной системе. Если, например, балка несет один сосредоточенный груз (рис. 15.34,а), масса которого значительно превышает массу самой балки, то в расчетной схеме системы естественно пренебречь массой балки и считать n=1.

Канонические уравнения колебания упругих систем с конечным числом степеней свободы

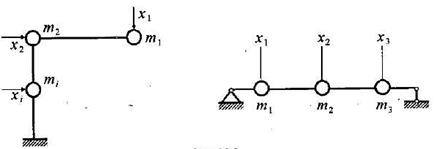
Рассмотрим упругую систему, несущую несколько сосредоточенных масс (i=1,2,…,i). Пусть - силы, приложенные к этим грузам в направлении их смещений (рис. 15.36).

Рис. 15.36

Тогда перемещения этих грузов в направлении приложенных сил по закону Гука и принципу независимости действия сил определяются по формулам:

или в сокращённой записи

Здесь - коэффициенты влияния, определяемые с помощью формулы Мора. Представим теперь, что наша система пришла в движение. Выясним природу сил в этом случае. На сосредоточенную массу может действовать внешняя сила , зависящая от времени и, согласно принципу Даламбера, - сила инерции . Следовательно,

Здесь точки над означают двукратное дифференцирование по времени. В свою очередь сила может состоять из постоянной (например, вес груза) и переменной частей:

Подставляя (15.67) в (15.66), получим форму записи уравнений движения упругих систем с конечным числом степеней свободы:

которые называются каноническими уравнениями колебаний упругих систем. При исследовании колебаний различают собственные (свободные) и вынужденные колебания. Под собственными колебаниями системы понимают такие, которые она совершает при отсутствии внешнего силового воздействия, т.е. предоставленная самой себе. В этом случае , и колебания поддерживаются только упругими силами. Под вынужденными колебаниями упругой системы понимают такие, которые происходят под действием возмущающих сил .

Собственные колебания упругих систем с конечным числом степеней свободы

В этом случае , и уравнения (15.69) принимают вид

Это система неоднородных дифференциальных уравнений второго порядка. В частном случае системы с одной степенью свободы (i=j=1) получим:

или, так как

где обозначено

Решение (15.72) будет:

где - частное решение уравнения (10.8), представляющее статическое перемещение массы, A - амплитуда колебания, - начальная фаза колебания, - круговая частота (рис. 15.37).

Время T одного колебательного движения точки называют периодом колебания. Величину , характеризующую число колебаний в единицу времени, - частотой колебаний.

Свяжем частоту колебаний с круговой частотой . Так как при изменении времени на T система приходит, вследствие периодичности движения, в одно и то же положение, то

или

откуда имеем:

а) б)

Рис. 15.37

Максимальное перемещение

где через

обозначен коэффициент динамичности.

Для определения A необходимо задать начальные условия:

при

Тогда

откуда

Динамические максимальные напряжения определяются на основании закона Гука и соотношения (15.76) по формуле:

Если число степеней свободы n>1, то решением (15.70) будет

где - частные решения, представляющие собой статические перемещения масс m, - амплитуды колебании этих масс (рис. 15.38).

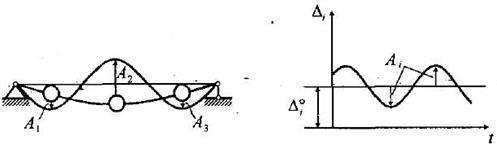
а) б)

Рис. 15.38

Подставляя выражения (15.81) в (15.70), найдем уравнения:

которые служат для определения собственных частот колебаний упругой системы с n степенями свободы.

Например, для системы с двумя степенями свободы (n=2) имеем:

Однородная система уравнений (15.82) имеет отличные от нуля решения только в том случае, если определитель, составленный из ее коэффициентов равен нулю:

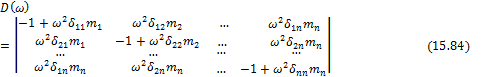
Определитель (15.84) после раскрытия приводит к уравнению степени n относительно , которое имеет n корней . Каждый корень дает частоту собственных колебаний упругой системы, причем их можно перенумеровать так, что

Коэффициенты динамичности

Выше мы рассматривали собственные колебания при отсутствии сил сопротивления. При таком предположении колебания продолжаются сколь угодно долго. В действительности всегда существуют силы (сопротивления воздуха, воды и др.), направленные против движения масс и приводящие к постоянному уменьшению амплитуды собственных колебаний вплоть до остановки движения. Предположим, что силы сопротивления пропорциональны первой степени скорости, т.е.:

В этом случае вместо уравнений (15.70) имеем:

В частном случае системы с одной степенью свободы имеем:

(

или, в силу

Решение уравнения можно (15.89) записать в виде:

где

Из (15.90) видно, что с ростом времени t амплитуда колебаний уменьшается, как показано на рис. 15.39, причем частота колебаний мало отличается от в силу малости величины n.

Рис. 15.39

Величина

является периодом колебаний, который больше, чем период колебаний T в отсутствие сил сопротивления. Через период колебаний отношение амплитуд будет равно:

или, логарифмируя, находим:

Как видим, амплитуда убывает по закону (15.93). Величину называют декрементом колебаний, а величину - логарифмическим декрементом. Аналогичные результаты получим для упругих систем при n>1.

Вынужденные колебания упругих систем с конечным числом степеней свободы.

Возмущающие силы представим в форме:

где - круговая частота возмущающей силы.

В этом случае канонические уравнения движения примут вид

В частном случае системы с одной степенью свободы (i=j=1) вместо (15.96) будем иметь:

или

Решением уравнения (15.98) будет:

где

Подставляя (15.99) в (15.98), найдем постоянную B:

откуда

Если учесть трение, то собственные колебания системы, определяемые в (15.99) первым слагаемым, со временем затухнут и для установившегося режима вынужденных колебаний будем иметь:

Величина B представляет собой амплитуду вынужденных колебаний. Максимальное перемещение:

где

- коэффициент динамичности. (15.104)

Максимальное динамическое напряжение

При имеем

Явление резкого увеличения амплитуды колебаний B и при совпадении частот собственных колебаний и возмущающей силы носит название резонанса, а само совпадение частот:

- условия резонанса. (15.106)

Возвратимся к системе с n степенями свободы. Решение системы уравнений (15.96) представим в виде

Подставляя (15.107) в (15.96), найдем:

Например, для системы с двумя степенями свободы (n=2) получим:

Решение системы (15.108) имеет вид

где определяется формулой (15.84), если заменить на

При будем иметь:

и поэтому амплитуды вынужденных колебаний т.е. имеет место резонанс.

В технике возмущающие силы бывают известны довольно редко. Обычно известна только их частота . Поэтому задача динамического расчета упругих систем сводится к определению собственных частот свободных колебаний с целью выявления возможности резонанса.

Приближенные методы определения низших частот собственных колебаний упругих систем

В большем числе случаев собственная распределенная масса упругих систем оказывается соизмеримой с присоединенными сосредоточенными массами. Поэтому сведение систем с бесконечным числом степеней свободы к системам с малым конечным числом степеней свободы оказывается не всегда приемлемым. В этих условиях предпочтительнее являются приближенные методы. Рассмотрим один из них – энергетический метод Релея.

Пусть имеется некоторая колебательная упругая система (рис.15.40, а) несущая собственный вес и несколько сосредоточенных масс . Наиболее опасной является первая форма колебаний, когда все массы колеблются в одной фазе (изогнутая ось 1 на рис. 15.40, б). В этом случае перемещения и напряжения в системе - наибольшие (мы отвлекаемся здесь от вопроса усталости материала, для которого существенными могут оказаться колебания с высокой собственной частотой).

Рассмотрим первую форму колебаний упругой системы. Если рассматривать колебания относительно статического положения равновесия системы, то закон движения любой точки упругой системы можно записать в виде

а) б)

Рис. 15.40

Перемещение массы будет:

На основании закона сохранения энергии для любых двух положений системы имеем:

где U - потенциальная энергия упругой системы,

- кинетическая энергия системы. (15.115)

Рассмотрим в качестве первого положения такое, при котором все массы проходят статическое положение равновесия. В этом положении и потенциальная энергия . Скорость

достигает максимального значения

Поэтому максимального значения достигает кинетическая энергия системы:

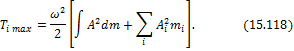
В качестве второго положения рассмотрим момент наибольшего отклонения системы от статического положения равновесия, когда кинетическая энергия , а потенциальная достигает своего максимального значения равенство (15.114) можно теперь написать на основании вышеприведенных рассуждений в виде :

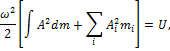
откуда получаем формулу Релея:

Для вычисления необходимо знать форму деформированного состояния упругой системы. Если задать ее приближенно, то этим самым мы как бы накладываем на систему дополнительные связи, т.е. делаем ее более жесткой. Вычисленная при этом частота со будет несколько завышенной по сравнению с точным значением. Если форму деформированного состояния угадать точно, то формула Релея даст точное значение низшей частоты колебаний упругой системы.

В случае изгиба балки для вычисления и имеем формулу:

В случае растяжения – сжатия стержня:

так как

Для случая кручения:

так как

Понятие о приведенной массе

Рассмотрим упругую систему, например балку с распределенной массой (рис. 15.41, а). Поставим следующую задачу. Какую массу нужно приложить в некоторой точке B такой же, но невесомой балки (рис. 15.41, б), чтобы низшие частоты колебаний исходной и упрощенной систем были одинаковы. Точку B назовем точкой приведения массы системы, а массу - приведенной массой.

а) б)

Рис. 15.41

Если - коэффициент жесткости системы, то ее потенциальная энергия:

Подставляя (15.125) в формулу Релея (15.119), получим:

С другой стороны, для системы с одной степенью свободы имеем

Сравнивая (15.126) и (15.127), получим:

Устойчивость вращающихся валов

Рассмотрим вал, вращающийся с угловой скоростью (рис. 15.42) и несущий сосредоточенные массы (диски).

Рис. 15.42

Будем считать, что он идеально сбалансирован и при вращении сохраняет прямолинейную форму. Если скорость вращения невелика, то малые случайные воздействия приводят вал к изгибным колебаниям, которые быстро затухают. В этих условиях прямолинейная форма вала устойчива. При некоторых больших скоростях вращения прямолинейная форма вала перестает быть устойчивой. Получив при этих скоростях вращения прогиб от случайного воздействия, вал уже не возвращается к своему исходному, прямолинейному состоянию. Он теряет устойчивость своей прямолинейной формы. Скорость , при которой впервые вал не возвращается к своему исходному состоянию при действии случайного воздействия, называется критической угловой скоростью вращающегося вала.

Предположим, что при действии возмущающих сил в смысле Эйлера, вал отклонился от своей прямолинейной формы и остался в искривленном состоянии. Тогда при его вращательном движении возникают центробежные силы инерции , приложенные к сосредоточенным массам, в каждый момент движения уравновешиваются упругими силами. Поэтому перемещение массы m, можно записать в виде:

Например, для системы с двумя сосредоточенными массами будем иметь:

Система (15.129) имеет отличные от нуля решения только в том случае, если определитель, составленный из ее коэффициентов, равен нулю:

В случае системы с n степенями свободы получим выражение (15.84), т.е. критическая угловая скорость вращения в точности совпадает с частотой собственных колебаний вала как балки.

В частности, для системы с одной степенью свободы имеем:

Явлению неустойчивости вращающихся валов можно дать и несколько иное истолкование. Идеально сбалансированных валов не бывает и в них, с самого начала вращения, возникают центробежные силы инерции, которые растут с увеличением . Следовательно, растут и перемещения (рис. 15.43,а).

а) б)

Рис. 15.43

Здесь имеем явление, аналогичное таковому при эксцентричном сжатии гибкого стержня (рис. 15.43,б).

Колебания упругих систем при действии ударной нагрузки

Ударными, или импульсивными, нагрузками будем называть такие, которые действуют в течение весьма короткого промежутка времени. Если он значительно меньше периода собственных колебаний упругой системы, то за время действия ударной нагрузки не произойдет заметных перемещений ее точек или масс, но они приобретут некоторые конечные скорости

Расчет упругих систем на ударную нагрузку можно разбить на два этапа:

1. Определение скоростей, которые получат точки системы сразу после удара.

2. Изучение свободных колебаний системы после удара при заданном распределении начальных скоростей.

Ударное нагружение происходит тогда, когда по упругой системе ударяет масса, движущаяся с некоторой скоростью .

Будем рассматривать в дальнейшем только неупругий или неосвобождающий удар, когда ударяющее тело не отскакивает от упругой системы, по которой совершается удар, а «прилипает» к нему и совершает вместе с ним как единое целое колебательное движение. Будем считать также, что конфигурация системы при ее движении после удара считается заранее известной и неизменной.

Удар по конструкции вертикально движущимся телом

Для наглядности рассмотрим не произвольную упругую систему, а тяжелую балку (рис. 15.44, а), на которую с высоты h падает груз массой M. Выберем у балки точку C, в которой происходит удар, за точку приведения массы и заменим балку с распределенной массой dm=qdz/g (q - вес единицы длины балки, g- ускорение свободного падения) балкой с одной приведенной массой (рис.15.44, б), т.е. заменим упругую систему с бесконечным числом степеней свободы на систему с одной степенью свободы. Обозначим через:

статический прогиб балки, соответствующий точке C в системе с приведённой массой, - жёсткость балки.

Пусть - скорость падающего тела в момент удара, а v - скорость приведённой массы и «прилипшего» к нему падающего тела сразу после удара. Если груз падает с высоты h, то . Из условия сохранения количества движения системы имеем:

откуда

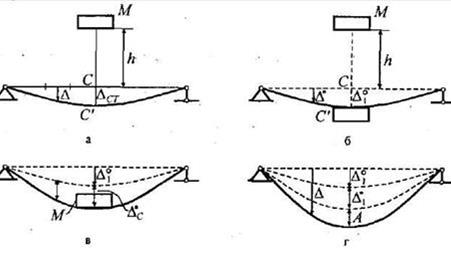
Рис. 15.44

Скорость v будет, с другой стороны, начальной скоростью объединенной массы () в ее колебательном движении после удара (2-й этап).

Пусть - статический прогиб балки в точке C от веса падающего груза Mg, т.е.

Тогда полный статический прогиб:

После удара начнётся колебательное движение упругой системы. По закону сохранения энергии сумма кинетической и потенциальной энергии системы при максимальном отклонении от статического положения равновесия перейдёт в потенциальную энергию деформации упругой системы:

где динамическое перемещение после удара,

т.к. по закону Гука; c – жёсткость упругой системы.

В результате получаем уравнение:

или, с учётом (15.133) – (15.135):

Решая полученное квадратное уравнение, находим:

где

- динамический коэффициент. (15.136)

В частности при внезапном ударе (n=0) имеем .

Можно иначе определить динамический коэффициент. Дифференциальное уравнение свободных колебаний системы после удара будет:

или

где

Решением уравнения (15.137) будет:

где

Закон движения (15.139) представлен на рис. 15.45.

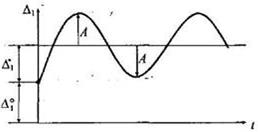
Рис. 15.45

Начальные условия колебательного движения системы после удара

Удовлетворяя решение (15.140) этим условиям, найдем:

или

откуда находим:

Найдем теперь максимальное отклонение системы от исходного состояния в ее колебательном движении:

Соотношение (15.142) можно записать

где

коэффициент динамичности. Он показывает во сколько раз прогиб от удара больше прогиба при статическом приложении того же груза.

Если то

В этом случае динамический коэффициент (105.144) принимает вид:

Выражение (15.144) совпадает с (15.136) при

По закону Гука

Следовательно, максимальное напряжение

где - напряжение в балке до удара груза - статическое напряжение от груза При имеем

Удар по конструкции горизонтально движущимся телом

Рассмотрим теперь удар по конструкции горизонтально движущимся со скоростью телом с массой M (рис. 15.46).

В этом случае

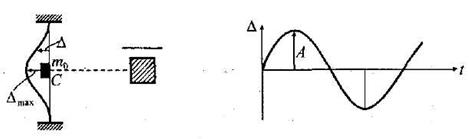
а) б)

Рис. 15.46

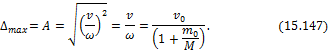
Закон движения:

представлен на рис. 15.46, б.

Зная можно всегда найти в упругой системе возникающие динамические напряжения.

Продольные колебания стержня

Перейдем теперь к изучению колебаний упругих систем с непрерывно распределенной массой, т.е. к системам с бесконечным числом степеней свободы. Простейшим примером такой системы является однородный стержень (рис. 15.47), в котором возбуждены продольные колебания, например, ударом по его концу.

Рис. 15.47

Пусть - плотность материала. Тогда масса элемента стержня длиной dz равна:

Осевое перемещение сечения:

w=w(z, t)

является функцией двух аргументов – координаты произвольного сечения x и времени t.

Используя принцип Даламбера, напишем уравнение движения элемента стержня:

или, с учётом (15.149),

Поскольку

то, исключив с помощью (15.151) из (15.150) усилие N, находим уравнение:

где

Уравнение (15.152) называется волновым уравнением. Оно описывает динамические процессы в стержне, такие как распространение волн и колебания. Величина называется скоростью распространения упругой волны. Для стали c= 4900 м/с, для алюминия c = 5100 м/с.

Решение уравнения (15.152) ищем в виде:

Подставляя (15.154) в (15.152), получим:

или, после разделения переменных:

откуда для функций T(t), Z(z) получаем обыкновенные дифференциальные уравнения:

Общий интеграл уравнения (15.156):

откуда видно, что - это круговая частота свободных колебаний.

Общий интеграл уравнения (15.157) имеет вид:

Постоянные находятся из граничных условий на концах стержня.

Пусть, например, стержень закреплен неподвижно на нижнем конце и свободен на верхнем (рис.15.48,а).

а) б)

Рис. 15.48

При Z=0 имеем W=0, а при Z=l имеем

Тогда получаем:

Если , то колебания отсутствуют. Если , то и тогда:

Стержень имеет бесконечное множество частот собственных колебаний. Низшая частота или частота основного тона имеет место при n=1:

Рассмотрим теперь колебания стержня, у которого один конец защемлён, а другой несет груз массы M (рис.15.48, б). На закрепленном конце при Z=0 по-прежнему имеем Z=0, из (15.159) следует .

На свободном конце с прикрепленной массой M на основании принципа Даламбера имеем:

или с учетом (15.104), (15.156):

Подставляя (15.159) при в граничное условие (15.164), находим:

Если , никаких колебаний нет. Если то колебания есть. Для удовлетворения условия (15.165) следует приравнять нулю квадратную скобку. В результате находим:

где через обозначена масса стержня. Решение уравнения (15.166) можно найти графически (рис. 15.49). Для этого необходимо найти точки пересечения двух функций:

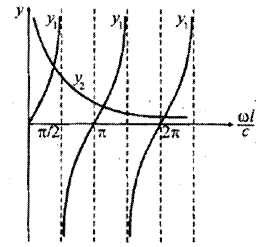
Рис. 15.49

При малых частотах, когда - малая величина, уравнение (15.166) упрощается:

откуда следует:

Этот результат соответствует задаче, когда массой стержня m можно пренебречь по сравнению с массой M груза.

Чтобы приближенно учесть массу стержня, удержим в разложении в уравнении (15.166) два слагаемых:

Тогда получим:

откуда

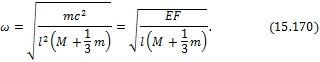
При больших значениях гипербола проходит близко к оси абсцисс, а точка пересечения с тангенсоидой мало отличается от Следовательно,

Поперечные колебания стержня

Рассмотрим поперечные колебания балки постоянного сечения с площадью F (рис. 15.50).

Рис. 15.50

Участок балки длиной dz имеет массу , где - плотность материала. Воспользуемся дифференциальным уравнением изогнутой оси балки четвертого порядка статической задачи:

При рассмотрении динамической задачи мы должны считать, что прогиб является функцией двух переменных z и t. Нагрузка q также должна зависеть от координаты z и времени t. Учитывая только инерционную силу и используя принцип Даламбера, вместо (15.171) получаем дифференциальное уравнение поперечных колебаний балки:

Как и в случае продольных колебаний, решение задачи ищем в виде:

Можно считать . Тогда после подстановки (15.173) в (15.172), получим уравнение

где

Решение уравнения (15.174) имеет вид

Постоянные А, В, С, D находим из граничных условий на опорах:

при z=0,

при z=l. (15.177)

Из первых двух условий имеем B=D=0. Из двух других находим:

Приравнивая нулю определитель системы уравнений (15.178), получим:

Так как только при , то остаётся принять:

или, согласно (15.175),

Из (15.178) при и следует c=0. Таким образом, при изгибных колебаниях балки образуется бесконечное число частот собственных колебаний, пропорциональных , где n – число полуволн изогнутой оси балки. Прогибы балки:

При колебаниях в основном тоне балка изгибается по одной полуволне (n=1). При n=2 имеем две полуволны, при n=3 – три (рис. 15.50).

Колебания балки в основном тоне (n=1) можно использовать для определения динамического модуля упругости материала, из которого изготовлена балка. Из (15.180) получаем:

где - частота колебаний.

Расчет на прочность при нерегулярной переменной нагруженности

Определение долговечности при нерегулярном нагружении производится обычно по следующей схеме. На первом этапе устанавливаются характеристики уровня нагруженности детали или элемента конструкции в виде функции распределения амплитуд эксплуатационных напряжений. В наиболее общем случае широкополосного процесса схематизацию случайного процесса с целью построения функции распределения амплитуд напряжений, эквивалентных случайному процессу по степени усталостного повреждения, производят одним из известных методов: максимумов, экстремумов, размахов, полных циклов, «дождя» и др. Метод полных циклов, например, дает, как принято считать, наряду с методом «дождя» наиболее приемлемые результаты для оценки долговечности при нерегулярном нагружении. Полученные величины амплитуд напряжений располагают в возрастающем порядке, образуя вариационный ряд амплитуд. По величинам амплитуд напряжений и соответствующим ординатам наносят точки на график и проводят через эти точки линию. На основании анализа опытных данных, обработка осциллограмм случайного процесса весьма часто приводит к эмпирическим функциям распределения амплитуд напряжений существенно отличающихся от нормального или какого-либо другого из известных законов распределения. Теоретический закон распределения амплитуд напряжений зависит от метода схематизации эксплуатационных нагрузок и во многих случаях оказывается трудно определимым.

Расчет на прочность при нерегулярной переменной нагруженности предполагает использование той или иной гипотезы накопления повреждений.

Например, корректированная линейная гипотеза накопления усталостных повреждений имеет следующий вид:

где - количество циклов действия данной амплитуды переменных напряжений за срок службы N_0.5;

- долговечность до разрушения или до образования трещины заданного размера при действии амплитуды (определяется по кривой усталости детали);

- корректированная сумма повреждений при действии всех повреждающих амплитуд переменных напряжений.

Значение определяется в зависимости от вида функции распределения действующих напряжений по следующей формуле:

где - элементарная вероятность попадания амплитуд в бесконечно малый диапазон

- функции распределения и плотности распределения действующих переменных амплитуд соответственно.

Профессором Когаевым В.П. получена формула для определения величины , которая зависит от особенностей спектра эксплуатационной переменной нагрузки:

где - максимальная амплитуда действующих напряжений; u – предел выносливости образца бесконечно большого диаметра или предельное повреждающее напряжение, принимаемое равным приблизительно половине предела неограниченной выносливости гладких лабораторных образцов стандартного размера:

Интегрирование в формуле (15.183) ведется по всем амплитудам вплоть до максимальной амплитуды действующего спектра или блока нагружения, превышающим предел неограниченной выносливости материала детали или элемента конструкции . Интегрирование в формуле (15.188) ведется по амплитудам, превышающим предельное повреждающее напряжение u. Схема расчета долговечности до разрушения иллюстрируется рисунком 15.51.

Окончательная формула для определения оценки среднего срока службы детали или долговечности до разрушения (образования трещины заданного размера) имеет на основании уравнений (15.183)-(15.188) следующий вид:

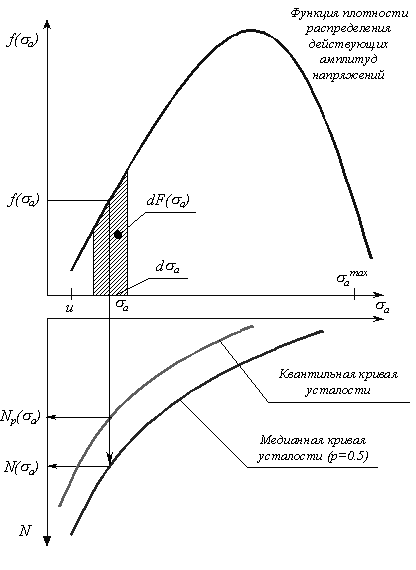
Рис. 15.51. Схема к расчету долговечности при нерегулярном переменном нагружении

Таким образом, для определения средней долговечности при нерегулярном переменном нагружении необходимо, во-первых, знать функцию распределения действующих напряжений, которая оценивается по результатам анализа спектра эксплуатационной переменной нагрузки одним из известных методов схематизации (метод размаха, максимумов, полных циклов и т.п.), во-вторых, иметь кривую усталости детали при регулярном переменном нагружении для определения долговечности, стоящей в знаменателе формулы (15.189).

Этого недостаточно для определения функции распределения долговечности при нерегулярном нагружении, которая представляет особый интерес в связи с необходимостью расчета гарантированного ресурса для ответственных деталей и элементов конструкций авиационной техники. С этой целью для оценки долговечности при нерегулярном нагружении, соответствующей вероятности разрушения p, в формуле (15.189) вместо медианной (p=0,5) долговечности должна использоваться долговечность (квантиль долговечности), соответствующая вероятности p, которая определяется по кривой усталости заданной вероятности разрушения (квантильной кривой усталости).

При варьировании величиной p получим функцию распределения долговечности до разрушения при нерегулярном переменном нагружении, общий вид которой представлен на рисунке 15.52.

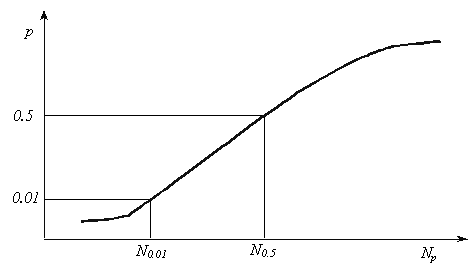
Рис. 15.52. График функции распределения долговечности до разрушения при нерегулярном переменном нагружении

Пример 3.

Построить функцию распределения долговечности до разрушения детали из алюминиевого сплава при нерегулярном нагружении, заданном распределением амплитуд спектра эксплуатационной нагрузки в соответствии с законом Рэлея:

где параметр s=30 МПа, максимальная амплитуда Эта функция представлена на рисунке 15.53.

Пусть медианная кривая усталости детали при симметричном цикле имеет следующий вид:

где параметры и A равны соответственно 50 и 1000 МПа.

Для расчета медианы долговечности достаточно этих данных. Для построения всей функции распределения необходимо располагать также параметрами квантильных кривых усталости, то есть кривых усталости, построенных по параметру вероятности разрушения. Так как построение семейства таких кривых требует большого числа экспериментальных данных, что не всегда возможно при длительных усталостных испытаниях, в первом приближении для вычисления квантили долговечности при регулярном нагружении воспользуемся известным приближением функции распределения логарифма долговечности на основании нормального закона:

где lgN_0.5 определяется по уравнению медианной кривой усталости, а среднее квадратическое отклонение примем постоянным и равным , что в первом приближении подтверждается большим числом экспериментальных данных усталостных испытаний деталей, элементов авиаконструкций и конструктивно подобных образцов из алюминиевых сплавов; - квантиль нормированного нормального закона распределения, соответствующая вероятности p. Тогда уравнение (15.190) для определения функции распределения ресурса при нерегулярном нагружении примет следующий вид:

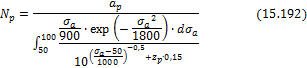
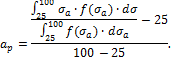
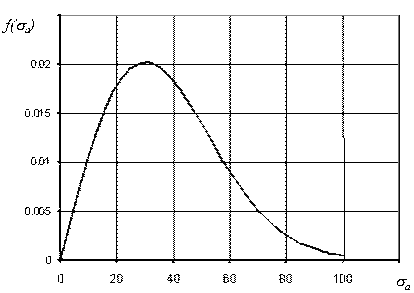
Рис. 15.53. Функция плотности распределения амплитуд спектра эксплуатационной нагрузки

Проведенный расчет функции распределения долговечности при нерегулярном переменном нагружении представлен в таблице 15.2.

В таблице 15.2 для примера представлен также расчет логарифма долговечности при той же нагруженности, но по степенному уравнению кривой усталости с нулевым значением предела неограниченной выносливости:

где параметр m=4, С=10^3,5. На рисунке 15.54 построены графики этих функций на нормальной вероятностной бумаге.

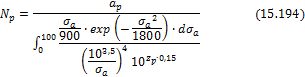
Отметим, что при расчете по уравнению (15.192) значение составило 0,283, а при расчете по уравнению (15.194) – 0,373. Кривые усталости для двух рассматриваемых в примере вариантов представлены на рисунке 15.55.

Таблица 15.2. Расчет функции распределения логарифма долговечности при нерегулярном нагружении

P	0.01	0.05	0.1	0.2	0.3	0.5	0.7	0.8	0.9	0.95	0.99
(15.192)	5.74	5.842	5.896	5.962	6.01	6.089	6.167	6.215	6.281	6.335	6.437
(15.194)	6.45	6.552	6.607	6.673	6.72	6.799	6.878	6.925	6.991	7.046	7.148

Основой расчета долговечности при нерегулярной нагрузке, как видно из рассмотренных выше примеров, является обоснование уравнения кривой усталости детали при регулярном нагружении. Наиболее надежным способом обоснования такой кривой усталости являются прямые усталостные испытания натурных деталей с последующей статистической обработкой их результатов. Как показывают расчеты для достижения достаточной точности оценивания характеристик усталостных свойств при усталостных испытаниях требуется порядка 30-50 объектов, что в условиях натурных испытаний является практически нереальным.

Рис. 15.54. Расчетные функции распределения логарифма долговечности при нерегулярном нагружении

по уравнениям (15.192) (линия 1), (15.194) (линия 2)

Рис. 15.55. Кривые усталости детали при симметричном нагружении, построенные

по уравнениям (15.192) (кривая 1), (15.194) (кривая 2)

В практике авиационных расчетных подразделений сложился комбинированный способ обоснования кривой усталости натурных деталей, суть которого заключается в выявлении опасных зон элемента конструкции (ресурсоограничивающих зон), изучении конструктивных и технологических особенностей этих зон, их нагруженности и последующего создания моделей или так называемых конструктивно-подобных образцов, которые по основным конструктивным, масштабным и другим характеристикам были бы подобны деталям в опасных зонах элемента конструкции. Испытаниям подвергаются в дальнейшем эти модельные образцы, стоимость которых ненамного выше обычных лабораторных образцов. В основном в качестве таких моделей в авиации используются для целей обоснования кривой усталости плоские образцы с отверстием, моделирующие масштабный эффект и концентрацию напряжений натурной детали. Полученная таким образом кривая усталости лишь приближенно отражает действительную кривую усталости элемента конструкции. Для уточнения такой кривой усталости по возможности следует проводить хотя бы единичные испытания натурной детали на одном уровне регулярной нагрузки. При этом в первом приближении можно считать, что показатель степени кривой усталости натурной детали равен показателю степени кривой усталости модельных образцов (то есть кривые усталости являются эквидистантными), но значение второго параметра уравнения кривой усталости, определяющего сдвиг одной кривой относительно другой, может быть уточнено.

Опыт показывает, что гипотеза линейного суммирования позволяет достаточно точно определить долговечность, если все амплитуды превышают предел выносливости материала детали и отсутствуют резкие всплески напряжений. Кроме того, опытами показано, что линейное суммирование повреждений подтверждается при монотонном увеличении амплитуд с ростом числа циклов, и действует иной закон накопления повреждений, если сначала приложить циклическую нагрузку с амплитудами, близкими к пределу текучести материала.

Таким образом, на долговечность существенно влияет история нагружения. Экспериментально установлено, что образец, нагруженный сначала циклическими напряжениями, меньшими предела выносливости, при дальнейшем повышении амплитуд малыми порциями показывает большую долговечность, чем исходная. В то же время предварительно перенапряжение образца циклическими напряжениями выше предела выносливости приводит к противоположным результатам. Однако вредное влияние перенапряжения начинает сказываться только после некоторого предельного числа циклов перенапряжения, зависящего от величины этих напряжений.

При случайном изменении амплитуд напряжений явления усталостного упрочнения и разупрочнения будут чередоваться и отчасти нивелироваться, что оправдывает в известной степени применение гипотезы накопления повреждений к таким нерегулярным режимам изменения напряжений.

Любой теоретический подход к проблеме долговечности конструкции при нерегулярном изменении напряжений требует экспериментальной проверки теоретических методов.

В настоящее время исследования проводятся по двум основным направлениям. Одно из них состоит в испытании непосредственно конструкций по программе нагружения, возможно ближе подходящей к экспериментально определенному спектру нагрузок.

Другое направление исследования состоит в испытании лабораторных образцов по различным ступенчатым программам циклического нагружения, в которых изменяется последовательность чередования нагрузок разной интенсивности с различным количеством циклов их действия. Исследуется влияние параметров нагрузки на долговечность образцов и полученные закономерности используются для оценки долговечности конструкций.

Вопросы для самопроверки

- Что называют усталостью материалов? В чем заключается физические причины усталости металлов?

- Почему многие детали машин имеют ограниченный срок службы (ресурс)?

- Как по виду излома детали узнать, что ее разрушение произошло от усталости?

- Объясните термин «долом»?

- Какие колебания называют собственными?

- Какой вид имеет формула динамического коэффициента при вынужденных колебаниях?

- Что такое условие резонанса?

- В чём заключается явление резонанса?

- Какие возможны решения для снижения динамических напряжений при вынужденных колебаниях?

- Опасно ли кратковременное попадание в зону резонанса деталей механизма при его разгоне?

- В чём опасность длительной работы конструкции при вынужденных колебаниях с частотой, близкой к частоте собственных колебаний?

- Объясните суть демпфирования системы.

- Перечислить все характеристики цикла и указать зависимость между ними.

- Какой из различных по форме циклов напряжений самый неблагоприятный для работы детали?

- Какие напряжения называются циклическими?

- Что называется циклом напряжений? Какими величинами характеризуется цикл?

- Какой цикл называется симметричным, статическим, пульсирующим?

- Какие циклы называют симметричным и отнулевым?

- Какие циклы нагружения деталей встречаются на практике?

- Что называется коэффициентом асимметрии цикла?

- Какие циклы вам известны?

- Какие параметры характеризуют цикл напряжений?

- Какие циклы называют подобными?

- Что представляет собой кривая усталостной прочности?

- Что называют пределом выносливости?

- Какую величину называют базовым числом циклов?

- Изобразите графики симметричного и отнулевого циклов изменения напряжений при повторно-переменных напряжениях?

- Перечислите характеристики циклов, покажите на графиках среднее напряжение и амплитуду цикла.

- Что характеризует коэффициент асимметрии цикла?

- В чем заключается принципиальное отличие между многоцикловой и малоцикловой усталостью?

- Что представляет собой кривая усталости? Как ее строить?

- Что такое предел выносливость материала? Как он определяется?

- Какие факторы влияют на предел выносливости материала?

- Как строится диаграмма усталостной прочности?

- Как определяется коэффициент запаса прочности при действии на деталь циклической нагрузки?

- Что понимается под полной кривой усталости? Какие зоны она имеет?

- Объясните принципиальную разницу между многоцикловой и малоцикловой усталости?

- Как ведутся испытания на малоцикловую усталость?

- Как определить предел выносливости, если допускаемая долговечность детали меньше базовой NG?

- Опишите характер усталостных разрушений?

- Что называется усталостью, выносливостью?

- Что называется пределом выносливости?

- Каковы особенности усталостного разрушения?

- Что называется усталостным разрушением и каковы его причины?

- Каково соотношение пределов выносливости при различных циклах нагружения?

- Влияние размеров, формы, шероховатости на величину предела выносливости.

- В чем заключается влияние абсолютных размеров поперечного сечения детали на предел выносливости?

- Почему на предел выносливости детали влияет шероховатость ее поверхности?

- Как учитывают совместное влияние различных факторов на предел выносливости детали?

- Как составить условие прочности для детали, работающей при асимметричном цикле нормальных или касательных напряжений?

- Как определить запас прочности детали при переменных напряжениях и сложном напряженном состоянии?

- От каких факторов зависит величина предела выносливости?

- Опишите порядок расчета детали на прочность при циклических напряжениях?

- Почему прочность при повторно-переменных напряжениях ниже, чем при постоянных (статических)?

- Что называют пределом выносливости? Как строится кривая усталости?

- Перечислите факторы, влияющие на сопротивление усталости?

- Как ведутся испытания на циклическую прочность?

- Для чего строится диаграмма предельных напряжений?

- Что представляет собой диаграмма предельных амплитуд?

- Как на диаграмме предельных амплитуд располагаются точки, соответствующие подобным циклам?

- Как схематизируют диаграмму предельных амплитуд?

- Сколько характеристик прочности материалов позволяют построить схематизированную диаграмму?

- Какие факторы влияют на усталостную прочность?

- Почему расчеты на усталостную прочность выполняются как поверочные?

- Как определяют коэффициент запаса усталостной прочности?

- Как определяют коэффициент запаса для детали, испытывающей одновременно циклические нормальные и касательные напряжения?

- В чем заключается эффект Баушингера?

- Что понимается под мягким и жестким нагружением образца?

- Какие конструкции на практике работают по принципу малоциклового нагружения?

- Как рассчитываются конструкции, работающие в малоцикловом режиме?

- Концентраторы напряжений. Как они влияют на предел выносливости?

- Что такое концентрация напряжений и в чём причина их возникновения?

- В чем заключается явление концентрации напряжений? В каких местах детали возникают концентрация напряжений?

- Почему концентрацию напряжений не учитывают при расчете на прочность деталей из пластичных материалов, работающих при статических нагрузках?

- Как определить эффективные коэффициенты концентрации напряжений?

- Что такое теоретический коэффициент концентрации напряжений и что такое эффективный коэффициент концентрации напряжений? От чего зависит величина того и другого?

- Каково влияние абсолютных размеров детали на её прочность? На предел выносливости?

- Как производится проверочный расчёт на прочность (определение фактического запаса) при переменных напряжениях?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00