Главная

Тестовые вопросы по теме «Геометрические характеристики простых плоских сечений»

- Какое из выражений используется для определения статического момента площади плоской фигуры?

1.

2.

3.

4.

- Каким может быть статический момент площади плоской фигуры?

1. Всегда больше нуля.

2. Всегда меньше нуля.

3. Всегда равен нулю.

4. Всегда равен нулю относительно центральных осей.

- Каким должен быть осевой момент инерции плоской фигуры?

1. Всегда меньше нуля.

2. Всегда больше нуля.

3. Всегда равен нулю относительно центральных осей.

4. Всегда равен нулю относительно главных осей инерции сечения.

- Каким может быть центробежный момент инерции плоской фигуры?

1. Всегда больше нуля.

2. Всегда меньше нуля.

3. Всегда равен нулю относительно главных осей инерции сечения.

4. Всегда равен нулю относительно центральных осей.

- Какая из фигур, изображенных на рисунке, имеет больший момент инерции относительно оси z, если обе фигуры имеют одинаковую площадь A=100 см²?

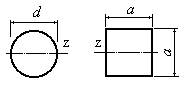
1. Фигура с круглым сечением.

2. Фигура с квадратным сечением.

- Как изменятся главные моменты инерции сечения квадратной формы при повороте осей на 45°?

1. Изменятся в 2 раза.

2. Не изменятся.

3. Изменятся в 3 раза.

4. Изменятся в 4 раза.

- Какой из формул следует воспользоваться при определении главных моментов инерции?

1.

2.

3.

4.

- Какими формулами следует воспользоваться при определении положения главных осей инерции?

1.

2.

3.

4.

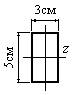
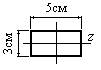
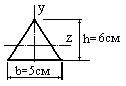
- Какое из представленных на рисунке поперечных сечений обладает большим осевым моментом инерции относительно горизонтальной оси z?

1.

2.

3.

4.

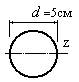
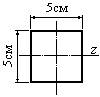
- У какой из этих фигур будет наименьший радиус инерции относительно оси z?

1.

2.

3.

4.

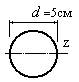
- Какое из представленных на рисунке поперечных сечений обладает большим полярным моментом инерции?

1.

2.

3.

4.

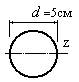
- Какая из перечисленных ниже геометрических характеристик определяет способность поперечного сечения балки сопротивляться внешним, нагрузкам не разрушаясь?

1. Осевой момент инерции?

2. Статический момент площади?

3. Полярный момент инерции?

4. Осевой момент сопротивления?

5. Центробежный момент инерции?

- Какой из формул следует пользоваться при определении осевого момента сопротивления?

1.

2.

3.

4.

- Чему равен полярный момент сопротивления сечения?

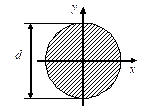
1.

2.

3.

- Чему равен осевой момент инерции сечения относительно центральной оси x?

1.

2.

3.

- Чему равен осевой момент инерции сечения относительно центральной оси x?

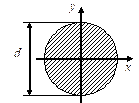
1.

2.

3.

- Чему равен момент сопротивления сечения относительно центральной оси x?

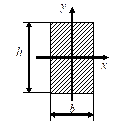
1.

2.

3.

- Полярный момент сопротивления W_р определяется как:

1.

2.

3.

4.

- Какое из выражений соответствует величине полярного момента инерции, если С равно отношению внутреннего диаметра кольца к внешнему:

1.

2.

3.

4.

- Статический момент площади сечения относительно центральной оси “Υ”

1) S_y >0;

2) S_y < 0;

3) S_y =0;

4) S_y ≠0.

- Для какой из осей статический момент сечения S будет наибольшим:

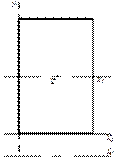
1) -у;

2) -х₁;

3) -х₂;

4) -х₃.

- Если I_y=I_z , а D_yz=0, то оси “y”,”z” являются:

1. центральными;

2. главными центральными;

3. осями симметрии;

4. главными.

- При повороте взаимно перпендикулярных осей “y”и”z” относительно общего начала координат сумма осевых моментов инерции (I_y+I_z):

1. зависит от угла поворота;

2. не изменяется;

3. равна нулю;

4. изменяется, но не зависит от угла поворота.

- Ось “y” изменила своё направление на противоположное. Значение какого момента инерции изменится:

1) I_y;

2) I_z;

3) D_yz;

4) I_p;

- Осевой момент инерции для треугольника будет максимальным для:

1) z₀;

2) z₁;

3) z₂;

4) z₃.

- Если I_y=I_z и D_zy=0, то главные оси инерции наклонены к исходным осям под углом:

1) α = 90°;

2) α = 30°;

3) α = 45°;

4) α = 60°;

- Выражение центробежного момента инерции плоского сечения относительно осей “y”и “z” имеет вид:

1)

2)

3)

4)

- Центробежный момент инерции сечения относительно главных осей:

1) D_zy > 0;

2) D_zy=0;

3) D_zy < 0;

4) D_zy ≠0.

- Осевой момент инерции круглого сплошного сечения определяется по формуле:

1)

2)

3)

4)

- Положение главных осей инерции определяется углом α₀, а tg 2α₀ равен:

1)

2)

3)

4)

- Осевой момент инерции треугольника высотой h и основанием b относительно оси “z”, проходящей через основание определяется по формуле:

1)

2)

3)

4)

- Если J_y < J_z , то при повороте осей на угол α₀ главная ось инерции, ближайшая к оси “z” будет осью:

1. симметрии;

2. максимума;

3. минимума;

4. нейтральной.

- При повороте осей на угол α, осевой момент инерции I_y, относительно повёрнутой оси “y”, можно вычислить по формуле:

1) I_z cos²α + I_y sin²α - D_yz sin2α;

2) I_y cos²α + I_z sin²α + D_yz sin2α;

3) D_yz cos2α – 0,5(I_y-I_z) sin2α;

4) I_z cos²α + I_y sin²α - D_yz sin²α.

- Где располагается центр тяжести тела, имеющего ось симметрии?

1. на оси симметрии;

2. положение центра тяжести нельзя определить.

- Чему равен статический момент сечения относительно оси y_c, проходящей через центр тяжести сечения?

1. ;

2. ;

3. .

- Какова размерность статического момента?

1. [длина]²

2. [длина]³

3. [длина]⁴.

- Может ли статический момент сечения быть отрицательным?

1. может

2. не может.

- Зависит ли статической момент площади от расположения площади относительно оси?

1. зависит;

2. не зависит.

- Может ли осевой момент инерции быть отрицательным числом?

1. может;

2. не может.

- Какова размерность осевых моментов инерции сечения?

1. [длина]²

2. [длина]³

3. [длина]⁴.

- Какие значения может приобретать осевой момент инерции I_z?

1. ;

2. ;

3. .

- Какой из моментов инерции сечения может быть отрицательным?

1. I_z

2. I_y

3. I_zy

4. I_p .

- Как изменится осевой момент инерции круга, если его диаметр увеличить в два раза?.

1. увеличится в 2 раза;

2. увеличится в 4 раза;

3. увеличится в 16 раз.

- Какую размерность имеет радиус инерции сечения?

1. [длина];

2. [длина]²;

3. [длина]³;

4. [длина]⁴.

- Относительно какой оси момент инерции треугольника будет минимальным?

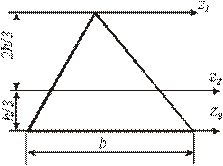
1. z₁;

2. z₂;

3. z₃.

- Если ось z₂ проходит через центр тяжести, то момент инерции относительно этой оси равен:

1. ;

2. ;

3. ;

4. .

- Момент инерции относительно оси z равен bh³/12. Чтобы вычислить момент инерции относительно оси z₁ необходимо воспользоваться формулой:

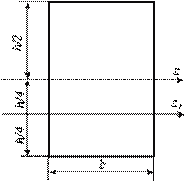
1. ;

2. ;

3. ;

4. .

- Если в поперечном сечении оси y,z являются главными, то относительно этих осей центробежный момент будет

1. максимальным;

2. минимальным;

3. равным нулю;

4. равен ∞.

- Влияние геометрических характеристик плоских сечений на прочность и жесткость элементов конструкции:

1. не влияют на прочность и жесткость;

2. зависит от направления внешней нагрузки;

3. от конфигурации сечения зависит величина напряжений и деформаций.

- Осевые моменты инерции:

1. сумма осевых моментов инерции величина постоянная;

2. сумма осевых моментов инерции величина не постоянная;

3. сумма осевых моментов инерции зависит от нагрузки.

- Осевой момент сопротивления круга:

1. ;

2.

3. .

- Осевой момент сопротивления прямоугольника:

1. ;

2. ;

3. .

- Полярный момент инерции кольца:

1. ;

2. ;

3. .

- Чему равен полярный момент круга?

1. ;

2. ;

3. ;

4. .

- Что такое статический момент площади поперечного сечения?

1. Статическим моментом сечения называется взятая по всей его площади А сумма произведений элементарных площадок на их квадрат расстояние то этой оси, т.е. .

2. Статическим моментом сечения относительно некоторой оси называется взятая по всей его площади сумма произведений элементарных площадок dA на из расстояние от этой оси: .

3. Статическим моментом сечения относительно некоторой оси называется взятая по всей его площади А сумма произведений элементарных площадок на их расстояние от этой оси:

4. Cтатическим моментом сечения относительно некоторой оси называется взятая по всей его площади А сумма произведений элементарных площадок dA на расстояние до двух взаимно-ортогональных осей: .

- Если (J_y и J_z=0) и (J_yz=0), то какие оси являются главными осями инерции?

1. Только оси max и min.

2. Оси системы координат y-z.

3. Любые оси, полученные поворотом системы координат (y-z).

4. Только главные центральные оси инерции.

- Чему равен статический момент относительно оси, проходящей через центр тяжести сечения?

1. S_z=0;

2. S_y=0, ;

3. S_y=0, S_z=0;

4.

- Если в плоскости сечения проведен ряд параллельных осей, относительно какой из них осевой момент инерции имеет наименьшее значение?

1. Относительно оси, проходящей через центр тяжести сечения.

2. Относительно оси, наиболее удаленной от центра тяжести сечения.

3. Относительно оси, где центробежный момент инерции равен 0.

4. Относительно оси, совпадающей с осью симметрии сечения.

- Статический момент сечения относительно оси “Х” определяется:

1.

2.

3.

4..

- Чему равен осевой момент инерции прямоугольника с размерами bxh относительно центральной оси “у”?

1. ;

2. ;

3. ;

4. .

- Чему равен осевой момент инерции круга относительно оси, проходящей через его центр тяжести?

1. ;

2. ;

3. ;

4. .

- Осевой момент инерции сечения относительно оси “Y” равен:

1. ;

2. ;

3. ;

4. .

- Какой интеграл определяет полярный момент инерции сечения?

1.

2. ;

3. ;

4. .

- Осевой момент инерции квадрата с размерами (аха) относительно центральной оси “Х” равен:

1. ;

2. ;

3. ;

4. .

- Какой знак имеют осевые моменты инерции?

1. положительный;

2. отрицательный;

3. равен нулю.

- Чему равен полярный момент инерции круга относительно его центра?

1. ;

2. ;

3. ;

4. .

- Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей?

1. ;

2. ;

3. ;

4. .

- Какой момент инерции может принимать отрицательные значения?

1. ;

2.

3. ;

4. .

- Чему равен статический момент сечения относительно оси, проходящей через центр тяжести сечения?

1. ;

2. ;

3. .

- Единицы измерения полярного момента инерции сечения.

1. см⁴;

2. см²;

3. см³;

4. см.

- Осевой момент инерции полукруга относительно основания равен:

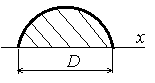
1. ;

2. ;

3. ;

4. .

- По какой формуле определяются положения главных центральных осей инерции сечения?

1. ;

2. ;

3. .

- Связь между осевыми и полярным моментами инерции

1. ;

2. ;

3. .

- Какова размерность центробежного момента инерции сечения?

1. см⁴;

2. см²;

3. см³;

4. см.

- Определить статический момент треугольника относительно оси, проходящей через основание.

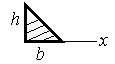
1. ;

2. ;

3. ;

4. .

- Осевой момент инерции прямоугольника с размерами bхh относительно центральной оси “Y” равен:

1. ;

2. ;

3. ;

4. .

- Осевой момент инерции треугольника относительно центральной оси Х_с, если его высота h и основание b, равен:

1. ;

2. ;

3. ;

4. .

- Определить относительно какой оси: х_с или у_с момент инерции прямоугольника больше, если размеры прямоугольника b и h (h>b).

1. х;

2. у_с;

3. х_с;

4. y .

- Центробежный момент инерции сечения в интегральной форме:

1.

2.

3.

4. .

- Теорема о параллельном переносе осей для центробежного момента инерции сечения записывается:

1. ;

2. ;

3. .

- Определить центробежный момент инерции прямоугольника, с размерами bхh, относительно осей, проходящих через центр тяжести сечения.

1. ;

2. ;

3. .

4. 0.

- Осевой момент инерции кольца с размерами dхD относительно центральной оси “Х” равен:

1. ;

2. ;

3. ;

4. .

- Осевой момент инерции сечения относительно оси “Х” равен:

1. .;

2. .;

3. .;

4. .

- Чему равен осевой момент инерции прямоугольника, с размерами bхh, относительно оси абсцисс, проходящей через центр тяжести прямоугольника?

1. ;

2. ;

3.;

4. ;.

- Если в плоскости сечения проведен ряд параллельных осей, относительно какой из них осевой момент инерции имеет наименьшее значение?

1. относительно оси, наиболее удаленной от центра тяжести сечения;

2. относительно оси, проходящей через центр тяжести сечения;

3. момент инерции не изменится.

- Как меняется момент инерции при параллельном переносе осей, если центральная ось “Х_с”

1. ;

2. ;

3. .

- Чему равен полярный момент инерции кольца относительно его центра?

1. ;

2. ;

3. ;

4. .

- Как изменится центробежный момент инерции при повороте осей координат на 90°?

1. ;

2. ;

3. .

- Какими формулами необходимо воспользоваться для определения координат центра тяжести сечения ?

1. и ;

2. и ;

3. нет правильного ответа.

- Изменится ли сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей при их повороте?

1. нет; ;

2. да; ;

3. да;

4. нет правильного ответа.

- Осевой момент инерции треугольника относительно оси проходящей через основание равен:

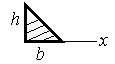
1. ;

2. ;

3. ;

4.

- Величины главных моментов инерции определяются по формуле:

Какая величина отсутствует в формуле?

1. ;

2. ;

3. ;

4..

- Будет ли равен нулю центробежный момент инерции сечения, имеющего одну ось симметрии?

1. нет;

2. да;

3. не зависит.

- Чему равен центробежный момент инерции относительно главных осей инерции?

1. J_ХУ >0;

2. J_ХУ <0;

3. J_ХУ =0.

- Что характеризует :

1. площадь сечения

2. напряжение при кручении

3. максимальный угол поворота

- Что характеризует и

1. моменты инерции при изгибе;

2. моменты инерции при кручении;

3. моменты инерции в опасных сечениях, соответственно вала и стержня.

- Влияние геометрических характеристик плоских сечений на прочность и жесткость элементов конструкции:

1. не влияют на прочность и жесткость;

2. зависит от направления внешней нагрузки;

3. от конфигурации сечения зависит величина напряжений и деформаций.

- Осевые моменты инерции:

1. сумма осевых моментов инерции величина постоянная;

2. сумма осевых моментов инерции величина не постоянная;

3. сумма осевых моментов инерции зависит от нагрузки.

- Относительно главной оси момент инерции принимает...

1. только наибольшее значение

2. только наименьшее значение

3. наибольшее или наименьшее значений

4. равен нулю

- Осевой момент сопротивления круга:

1. ;

2. ;

3. .

- Осевой момент сопротивления прямоугольника:

1. ;

2. ;

3. .

- Полярный момент инерции кольца:

1. ;

2. ;

3. .

- Интегралы называются...

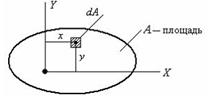
1. осевыми моментами инерции плоской фигуры

2. статическими моментами площади плоской фигуры

3. центробежными моментами инерции плоской фигуры

4. полярными моментами инерции плоской фигуры

- D=2 см. Момент инерции круга относительно оси x равен...

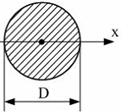
1. ;

2. ;

3. ;

4.

- Главные центральные оси инерции проходят через точку...

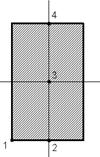
1. 2

2. 1

3. 3

4. 4

- Момент инерции прямоугольника относительно оси z равен...

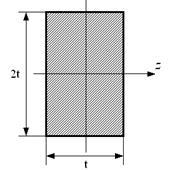
1. ;

2. ;

3. ;

4.

- Дано h=3b. Найти

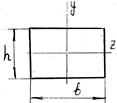
1. 2;

2. 3;

3. 6;

4. 8;

5. 9.

- Диаметр сплошного вала увеличен в 3 раза. Во сколько раз увеличились главные центральные моменты инерции?

1. в 6 раз;

2. в 81 раз;

3. в 3 раза;

4. в 9 раз.

- Диаметр сплошного вала уменьшен в 4 раза. Во сколько раз изменится полярный момент инерции вала?

1. уменьшится в 4 раза;

2. увеличится в 4 раза;

3. уменьшится в 64 раза;

4. уменьшится в 256 раз.

- Определить величину полярного момента инерции сечения, если главные центральные моменты инерции соответственно равны I_x = 7 см⁴, I_y = 3,5 см⁴

1. 7 см⁴;

2. 3,5 см⁴;

3. 10,5 см⁴;

4. 24,5 см⁴.

- Для данного сечения – швеллер № 10 определить :

а) осевой момент инерции сечения относительно оси X₀;

б) осевой момент инерции сечения относительно оси Y₀.

а)

1. 43 см⁴;

2. 186 см⁴;

3. 446,5 см⁴;

4. 20,4 см⁴;

б)

1. 43 см⁴;

2. 186 см⁴;

3. 446,5 см⁴;

4. 20,4 см⁴.

- Определить центробежный момент инерции прямоугольника с размерами в = 5 см, h = 10 см относительно осей проходящих через его стороны.

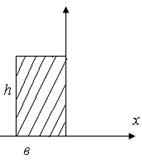
1. – 416,7 см⁴;

2. – 625 см⁴;

3. 432 см⁴;

4. 625 см⁴.

- Определить моменты инерции сечения относительно центральных осей х_С и у_С, с = 5 см

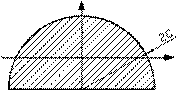
1.

2.

3.

4.

- В каком случае значение I_x минимально?

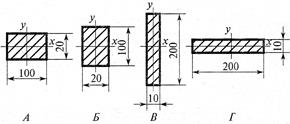
1. А;

2. Б;

3. В;

4. Г.

- Рассчитать осевой момент инерции двутавра относительно оси, проходящей через основание

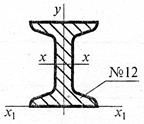
1. 350 см⁴;

2. 879,2 см⁴;

3. 438,2 см⁴;

4. 1317,2 см⁴.

- В каком случае значение I_y максимально?

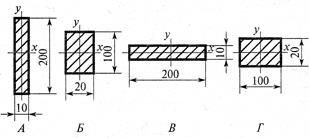
1. А;

2. Б;

3. В;

4. Г.

- Определить полярный момент инерции сечения, если осевой момент инерции I_x = 14 см⁴

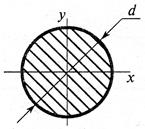
1. 7 см⁴;

2. 36 см⁴;

3. 14 см⁴;

4. 28 см⁴.

- Рассчитать осевой момент инерции швеллера относительно оси, проходящей через основание

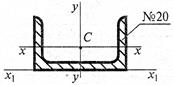
1. 113 см⁴;

2. 1419 см⁴;

3. 1620,3 см⁴;

4. 213,3 см⁴.

- Рассчитать осевой момент инерции двутавра относительно оси х₁

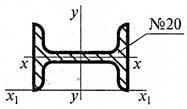
1. 785 см⁴;

2. 1170 см⁴;

3. 249 см⁴;

4. 1840 см⁴.

- В плоскости поперечного сечения – это равнобедренный треугольник АВС – проведены четыре оси (x₁, x₂, x₃ и y₁), две из которых (x₂ и y₁) проходят через центр тяжести площади. Если принять h=3b, то наибольшим будет момент инерции площади относительно оси:

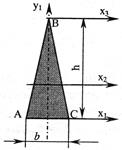
1. x₁;

2. x₂;

3. x₃;

4. y₁.

- Если поперечное сечение стержня задано в форме ромба, то отношение величин главных центральных моментов инерции сечения (I_x/I_y) равно:

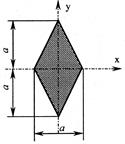
1. 2,0;

2. 2,4;

3. 3,0;

4. 4,0.

- На чертеже изображено поперечное сечение в виде уголкового профиля. Момент инерции сечения I_x относительно оси симметрии (Ox) равен:

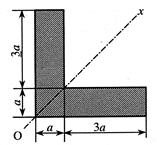
1. 16,6 a⁴;

2. 14,6 a⁴;

3. 12,6 a⁴;

4. 10,6 a⁴.

Онлайн-калькулятор "Расчет геометрических характеристик равнобедренного треугольника"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00