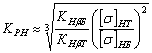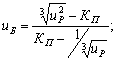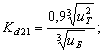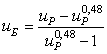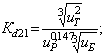Главная
Раздел 19.
Параметрическая оптимизация одно- и многоступенчатых редукторов
Зубчатые передачи, как составная часть механического привода, имеют широкое применение в технике. При этом, детали вращения в машинах составляют примерно одну треть от общего количества всех деталей; в этой связи любая научно – исследовательская работа, направленная на повышение надежности, квалиметрических характеристик и снижение их масс является актуальной.
Обычно при проектировании многоступенчатых зубчатых передач проводят параметрическую оптимизацию для заданной схемы привода. В процессе многокритериальной оптимизации возникают не только сложности, но и неопределенности, не поддающиеся анализу, поэтому, на наш взгляд, целесообразно проводить ее поэтапно. На первом этапе при выборе варианта привода с равнопрочными ступенями при различных частотах вращения вала электродвигателя, критерием оптимальности для разбивки общего передаточного числа редуктора по ступеням необходимо выдержать следующие условия: компактность, обеспечение нормальной смазки с наименьшими потерями на разбрызгивание и минимальной суммарной массы зубчатых колес, ограничение максимального передаточного отношения быстроходной ступени из условия изгибной прочности.
На втором этапе проектирования проверяются такие конструктивные ограничения, как технологичность быстроходного вала - шестерни, достаточность зазора между колесами и валами с обеспечением их необходимой жесткости, возможность размещения между подшипниками стяжных винтов крышки и основания корпуса редуктора. При этом составляется эскизная компоновка и проверяются подшипники качения на достаточность требуемого ресурса.
Задача данного раздела сводится к проведению оптимизации параметров редукторов без проверки на обеспечение конструктивных ограничений, что дает возможность для широкого внедрения автоматизированного проектирования для таких типов механизмов.
Проектный расчет привода с одноступенчатыми редукторами и открытыми передачами
Для одноступенчатых редукторов ряд конструктивных ограничений выпадает в силу их особенностей устройства и основные требования сводятся к следующему: наименьшие масса, габариты и стоимость, наибольший КПД, обеспечение жесткости, надежности, квалиметрических требований и конструктивных ограничений.
Необходимо отметить, что одноступенчатые редукторы часто применяются, как объект курсового проектирования, совместно с открытыми передачами (ременные или цепные, редко зубчатые), поэтому диаметр шкива (или звездочки d0), размещенного на валу редуктора, не должны превышать более, чем на 20% диаметр вершин зубьев колеса (d0 = 1,2 da2). Это ограничение вызвано необходимостью установки кожуха для открытых передач, размеры которых не должны выходить за пределы рамы или плиты.
Обычно проектный расчет привода проводят с помощью пакета прикладных программ на ЭВМ в два этапа. Это затрудняет применение САПР, в этой связи надо рассмотреть проектный расчет с конструктивных ограничений.
Под конструктивными ограничениями понимают прежде всего возможность изготовления зубьев шестерни и обеспечение необходимой прочности и жесткости быстроходного вала, возможность размещения в корпусе редуктора стяжных винтов между подшипниками валов. Чем больше передаточное число редуктора – uред и выше поверхностная твердость зубьев, тем труднее удовлетворить конструктивным ограничениям.
Исходя из условия обеспечения необходимой прочности и жесткости
предлагается вычислять диаметр – d
(мм) концевого участка быстроходного вала:
![]() (1)
(1)
где К=7 для
цилиндрических и К=8 для конических
передач; ТБ – вращающий
момент на валу в Нм.
Однако, необходимо помнить, что диаметр выходного конца не должен
отличаться от диаметра электродвигателя
более ![]() при соединении с
помощью муфты.
при соединении с
помощью муфты.
Для обеспечения жесткости вала желательно выполнение условия:
- для шестерни цилиндрической передачи редуктора диаметр впадин
df1=1,25d; (2)
- для шестерни конической передачи средний диаметр
dm1=1,35d (3)
- для передвижной цилиндрической блок – шестерни коробки передач
df1=1,8d; (4)
здесь d – диаметр выходного конца вала.
В качестве критерия оптимальности наиболее часто применяют массу и стоимость редуктора.
Обычно расчет зубчатых передач проводят для нескольких сочетаний твердостей, варьируемых при этом :
I – улучшение шестерни и колеса (У1+У2).
II – закалка шестерни и улучшение колеса (З1+У2).
III - закалка шестерни и колеса (З1+З2)
или цементация шестерни и закалка колеса
(Ц1+З2).
- коэффициент
ширины зубчатого венца ![]() для КПП и
для КПП и ![]() для одноступенчатого
редуктора.
для одноступенчатого
редуктора.
- u1, u2, u3… распределение общего передаточного числа между передачами.
Цилиндрический одноступенчатый редуктор
Для анализа
определяется диаметр выходного быстроходного вала по формуле (8.1) и
сравнивается с диаметром вала электродвигателя. При этом диаметр вала редуктора
не должен отличаться более чем на ![]() . Для единичного производства
можно рекомендовать I – группу термообработки (У1+У2)
при этом
. Для единичного производства
можно рекомендовать I – группу термообработки (У1+У2)
при этом ![]() можно принять 0,5. При
применении термообработки II – группы можно принять
можно принять 0,5. При
применении термообработки II – группы можно принять ![]() , для III – группы
, для III – группы ![]() . Указанные коэффициенты относительной ширины обычно
обеспечивают конструктивные ограничения, это условие размещения стяжных винтов
между подшипниками. После определения межцентрового расстояния -
. Указанные коэффициенты относительной ширины обычно
обеспечивают конструктивные ограничения, это условие размещения стяжных винтов
между подшипниками. После определения межцентрового расстояния - ![]() можно определить массу
и стоимость редуктора по формуле:
можно определить массу
и стоимость редуктора по формуле:
![]() (5)
(5)
где ![]() – межцентровое
расстояние в м;
– межцентровое
расстояние в м;
КТ – коэффициент, учитывающий группу термообработки (из табл.1);
е=2,71 – основание натурального логарифма.
Стоимость
редуктора определяется по выражению в У.Е.:
 (6)
(6)
здесь КС – коэффициент стоимости с учетом затрат на термообработку (из табл. 1);
N – годовая программа, шт/год.
Таблица 1
|
Группа термообработки |
I |
II |
III |
|
КТ |
0,1 |
0,2 |
0,3 |
|
КС |
3,15 |
3,3 |
3,8 |
Рациональной конструкцией редуктора при постоянных передаточном числе и термообработке следует считать вариант с минимальной массой, а при различной термообработке вариант с минимальной стоимостью и удовлетворяющий следующим конструктивным ограничениям:
- диаметр впадин зубьев шестерни должен удовлетворять условию (2);
- обеспечение соразмерности редуктора и деталей, устанавливаемых на концах входного или выходного валов шкива или звездочки;
- должно быть обеспечено размещение стяжных винтов между подшипниками.
При наличии открытой гибкой или зубчатой передачи в приводе для установления эффективного варианта с электродвигателем различной частотой вращения достаточно определения суммарной массы или стоимости редуктора и электродвигателя, так как масса и стоимость рамы, муфты и открытой передачи незначительно изменяются от общего передаточного числа привода.
Масса
электродвигателя в кг определяется по формуле,
предлагаемой нами.
 (7)
(7)
где ![]() - показатель;
- показатель;
![]() - комплексный показатель;
- комплексный показатель;
h-высота электродвигателя от оси вращения до плоскости крепления электродвигателя в метрах; указывается в марке асинхронного трехфазного электродвигателя общего назначения, например 4А132М6, здесь h=132 мм =0,132 м и р=6 – число полюсов;
е = 2,71 – основание натурального логарифма;
nc – синхронная частота вращения двигателя, об/ мин.
Nэ- мощность электродвигателя в кВт;
Стоимость
электродвигателя в У.Е.:
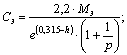 (8)
(8)
Конический одноступенчатый редуктор
При выборе рациональной конструкции с постоянным передаточным числом необходимо отдать предпочтение варианту с меньшей массой, удовлетворяющему следующим конструктивным ограничениям:
-
удовлетворение условий (3);
- обеспечение
максимального диаметра шкива или звездочки, размещенной на валу редуктора ![]() ;
;
Следует проанализировать влияние способа термообработки зубчатых колес на их массу – mК, массу редуктора – МР, внешнее конусное расстояние – Re, внешний диаметр вершин зубьев колеса – dае2, средний делительный диаметр шестерни – dm1, на окружную силу в зацеплении – Ft.
При наличии в приводе других передач оптимальный вариант устанавливается через суммарную массу или стоимость редуктора и электродвигателя.
Масса для
нового поколения редукторов определяется по следующему выражению в кг:
![]() (9)
(9)
где dе2 – внешний делительный диаметр колеса, м;
КМ – коэффициент массы, КМ =4000 для широких редукторов типа К1Ш при uP =1,25...2,8;
![]() - показатель для К1Ш. Для редукторов К1
при uP
=3,15...5 КМ =2250 и
- показатель для К1Ш. Для редукторов К1
при uP
=3,15...5 КМ =2250 и ![]() .
.
Стоимость
редуктора в У.Е. по формуле (6):

здесь КС – коэффициент стоимости с учетом затрат на термообработку (из табл. 2);
Таблица 2
|
Группа термообработки |
I |
II |
III |
|
КС |
5,9 |
6,2 |
7,2 |
Червячный редуктор
В этом случае
следует проанализировать влияние
материала колеса на суммарную массу колеса и червяка – mКЧ, массу редуктора – МР, межосевое расстояние - ![]() , КПД, температуру масла в редукторе – tМ.
, КПД, температуру масла в редукторе – tМ.
Наиболее целесообразной является конструкция с возможно меньшей массой и большим КПД при допустимой температуре масла в редукторе.
Масса
редуктора определяется по следующей формуле в кг:
![]() (10)
(10)
здесь ![]() – межосевое расстояние
редуктора в м.
– межосевое расстояние
редуктора в м.
Стоимость
редуктора в У.Е.:

здесь КС – коэффициент стоимости с учетом термообработки червяка (шлифования и полирования) (из табл.3);
Таблица 3
|
Термообработка червяка |
НЧ<350НВ - улучшение |
НЧ>45НRCЭ - закалка |
НЧ>50НRCЭ - цементация |
|
КС |
5,9 |
6,2 |
7,2 |
Планетарный редуктор
Следует
проанализировать влияние способа термообработки и относительной ширины колес
на массу зубчатых колес– mК, массу редуктора
– МР, межосевое расстояние
- ![]() , диаметры окружностей
впадин зубьев колеса солнечной шестерни– dfa, сателлита – dfд,
и эпицикла – dfb.
, диаметры окружностей
впадин зубьев колеса солнечной шестерни– dfa, сателлита – dfд,
и эпицикла – dfb.
В качестве рационального нужно выбрать вариант с меньшей массой, но с возможностью размещения подшипника в сателлите, соразмерностью солнечной шестерни, выходного вала и эпицикла, а также деталей, устанавливаемых на конце выходного вала.
Проектный расчет параметров цилиндрических двухступенчатых
редукторов типа Ц2У, Ц2 общего назначения
Теоретические
основы проектного расчета по определению передаточного отношения каждой ступени
многоступенчатых цилиндрических передач по развернутой схеме из условий
равнопрочности и компактности известны с 60-х годов.
Равенство диаметров колес ступеней ![]() редукторов типа
Ц2У при обеспечении компактности даст следующее уравнение:
редукторов типа
Ц2У при обеспечении компактности даст следующее уравнение:
![]() (11)
(11)
здесь![]() - коэффициент загруженности редуктора по контактному
напряжению.
- коэффициент загруженности редуктора по контактному
напряжению.
Совместное
решение (11) и общеизвестной зависимости общего передаточного числа редуктора -
up:
![]() ;
(12)
;
(12)
при Кр=1 даст следующее решение:
Передаточное число быстроходной ступени
![]() (13)
(13)
Передаточное
число тихоходной ступени
![]() (14)
(14)
Действительно,
согласно старому стандарту ГОСТ 21354-75 при неограниченном сроке службы
редуктора, коэффициенты долговечности зубчатых колес были равны единице, так
как правая ветвь кривой выносливости Велера была параллельна к оси абсцисс.
Значение коэффициентов нагрузки - Кн были меньше, чем по стандарту ISO 6336. При равенстве
коэффициентов ширины колес ![]() , коэффициент нагруженности редуктора по
контактному напряжению был близок к единице.
, коэффициент нагруженности редуктора по
контактному напряжению был близок к единице.
Необходимо
отметить, что при ![]() и
и ![]() рассуждение о
равенстве коэффициентов отношения ширины колеса к диаметру шестерни
рассуждение о
равенстве коэффициентов отношения ширины колеса к диаметру шестерни ![]() не имеет места.
не имеет места.
Как указывает В. Вольф, одна из задач, возникающих при конструировании многоступенчатых редукторов, заключается в выборе такого распределения передаточных чисел между ступенями, которое обусловило бы минимальные размеры редуктора. Существенным показателем, определяющим габариты редуктора с цилиндрическими колесами, является сумма межосевых расстояний между валами.
Межцентровое
расстояние для одноступенчатого редуктора определяется из выражения
![]()
Сумма межосевых расстояний для многоступенчатой передачи
![]() (15)
(15)
В предположении, что число зубьев шестерен в каждой ступени одинаково, то есть принимая, что Zш1= Zш2= Zш3= Zш4, выражение (15) примет вид
![]() (16)
(16)
Модули зубьев
могут быть определены из условия изгибной прочности:
![]() (17)
(17)
где ТШF - расчетный крутящий момент на шестерне в Нмм;
![]() - коэффициент нагрузки
при расчете на изгибную выносливость;
- коэффициент нагрузки
при расчете на изгибную выносливость;
![]() - коэффициент формы
зуба;
- коэффициент формы
зуба;
![]() диаметр начальной окружности шестерни в мм;
диаметр начальной окружности шестерни в мм;
![]() ширина зубчатого колеса, выраженная через число модулей.
ширина зубчатого колеса, выраженная через число модулей.
Из уравнения
(17) модуль передачи будет
![]() (18)
(18)
Соотношение модулей двух
последовательных ступеней при Zш1= Zш2 и ![]() (рис. 1)
(рис. 1)
![]() (19)
(19)
здесь ![]() - отношение
коэффициентов нагрузки при изгибе зубьев тихоходной ступени к
быстроходной;
- отношение
коэффициентов нагрузки при изгибе зубьев тихоходной ступени к
быстроходной;
![]() - отношение
допускаемого напряжения шестерни быстроходной ступени к
тихоходной.
- отношение
допускаемого напряжения шестерни быстроходной ступени к
тихоходной.
Следует
отметить, что ![]() и
и ![]() , так как
, так как ![]() и правая ветвь кривой усталости имеет некоторый наклон,
поэтому произведение этих величин меньше единицы, но извлечение из
него кубического корня дает величину близкую к единице.
и правая ветвь кривой усталости имеет некоторый наклон,
поэтому произведение этих величин меньше единицы, но извлечение из
него кубического корня дает величину близкую к единице.
Подставляя выражение (19) в уравнение (16) получают величину суммарного межцентрового расстояния
 (20)
(20)
Как известно,
общее передаточное число механизма будет
![]() ; (21)
; (21)
Для того,
чтобы найти экстремальные значения суммарного межцентрового
расстояния, как функции от передаточного числа ступеней (аwc=f (u1; u2,
u3,... uк), в которой
переменные u1,
u2, u3... uк связаны между
собой зависимостью ![]() применим метод Лагранжа. Функция
применим метод Лагранжа. Функция ![]() ищется в виде
уравнения:
ищется в виде
уравнения:
![]() (22)
(22)
где ![]() - неизвестный множитель.
- неизвестный множитель.
Условия
экстремальных значений функции F имеют вид:
![]() (23)
(23)
где К=1,2…n
Решение для
двухступенчатого редуктора дает следующую зависимость между передаточными
отношениями при ![]()
![]() (24)
(24)
Совместное
решение с уравнением ![]() дает выражение
дает выражение
![]() (25)
(25)
Решение данного уравнения на ЭВМ представлено на рис. 2 в виде графика.
Выражение (20) может иметь другой вид
 (20,а)
(20,а)
Зависимость суммарного межцентрового расстояния ![]() в относительных
единицах для двухступенчатого редуктора типа Ц2У от передаточного числа
быстроходной ступени показана на рис. 3. График при передаточных числах
редуктора от 8 до 40 имеет ярко выраженный минимум. Зависимость передаточного
числа тихоходной ступени от общего передаточного отношения редуктора показана
на рис. 2.
в относительных
единицах для двухступенчатого редуктора типа Ц2У от передаточного числа
быстроходной ступени показана на рис. 3. График при передаточных числах
редуктора от 8 до 40 имеет ярко выраженный минимум. Зависимость передаточного
числа тихоходной ступени от общего передаточного отношения редуктора показана
на рис. 2.
С точки зрения минимума суммарного межцентрового расстояния представляет интерес определение границы целесообразного перехода с одноступенчатого редуктора на двухступенчатый, с двух- на трехступенчатый и т.д.
Для
одноступенчатого редуктора межцентровое расстояние составляет
![]() (26)
(26)
для
двухступенчатого
![]() (27)
(27)
Приравнивание ![]() дает
условие, определяющее границу перехода в виде:
дает
условие, определяющее границу перехода в виде:
![]() (28)
(28)
Это уравнение, с учетом выражения (25), дает предельное отношение u=8,64 для одноступенчатого редуктора из условия изгибной прочности зубьев, выше которого целесообразен переход на двухступенчатый редуктор, независимо от числа зубьев шестерни.
Аналогично установлены границы перехода с двух на трехступенчатую схему, начиная с u=41,1 а при u=160 на четырехступенчатую схему.
Исследованием многоступенчатых редукторов по развернутой схеме занимался также профессор Ниманн Г.. Из условий изгибной прочности и минимального суммарного межцентрового расстояния для двух- и трехступенчатых редукторов передаточное число быстроходной ступени, а для трехступенчатой схемы также передаточное число промежуточной ступени показаны штрихпунктирной линией на графике рис.4. Ранее рекомендованные области по проектированию многоступенчатых передач для практики заштрихованы, и как видим, имеют завышенные значения передаточных чисел ступеней.
Следует отметить, что для трехступенчатых передач при общем передаточном числе до 100 передаточное число быстроходной ступени меньше промежуточной.
Согласно ГОСТ
21354-87, контактная выносливость зубчатых передач определяется по формуле:


Рис. 1
Рис.2

Рис.3

Рис. 4. Зависимость от общего передаточного
числа
редуктора передаточных чисел ступеней
Из этого выражения допускаемый момент на колесе:

где  - комплексный коэффициент, учитывающий контактные напряжения,
характер нагружения и механических свойств материалов зубчатой пары.
- комплексный коэффициент, учитывающий контактные напряжения,
характер нагружения и механических свойств материалов зубчатой пары.
Отсюда
![]() (29)
(29)
Масса зубчатой
пары через объем и удельную массу – ![]() будет
будет
![]() (30)
(30)
После
подстановки из выражения (29) ![]() уравнение примет вид
уравнение примет вид
![]()
или
![]()
или
![]()
где ![]() – параметр массы
зубчатых колес в относительных выражениях.
– параметр массы
зубчатых колес в относительных выражениях.
Для многоступенчатых передач данное выражение при
умножении правой и левой части на ![]() примет вид:
примет вид:
![]()
Для того чтобы
найти экстремальные значения суммарной массы зубчатых передач, как функции ![]() в которой переменные
связаны между собой зависимостью
в которой переменные
связаны между собой зависимостью ![]() применен метод
Лагранжа и функция ищется
применен метод
Лагранжа и функция ищется ![]() , имеющий вид
, имеющий вид
![]()
где ![]() - неизвестный множитель.
- неизвестный множитель.
Условия экстремальных
значений функций F запишется в виде
![]()
где К=1,2,3,…n.
Выражение для
определения параметра суммарной массы передач упростится, если подставить
значение комплексных коэффициентов для всех ступеней и считать материалы
шестерен, а также всех колес одинаковыми
 (31)
(31)
здесь ![]() - коэффициент
нагрузки каждой ступени;
- коэффициент
нагрузки каждой ступени;
![]() - допускаемый контактный предел выносливости
зубчатой пары каждой ступени.
- допускаемый контактный предел выносливости
зубчатой пары каждой ступени.
При ![]() и
и ![]() для одно-, двух- и
трехступенчатых передач параметры массы зубчатых колес в относительных
единицах, в зависимости от передаточного числа быстроходной ступени, приведены
на рис.5, 6 и 7.
для одно-, двух- и
трехступенчатых передач параметры массы зубчатых колес в относительных
единицах, в зависимости от передаточного числа быстроходной ступени, приведены
на рис.5, 6 и 7.
Действительно,
для выражения (31) по старому стандарту ГОСТ 21354-75 отношение комплексных
коэффициентов ступеней можно было принять равным единице для зубчатых передач с
неограниченным сроком службы, так как правая ветвь кривой контактной усталости
была горизонтальной к оси абсцисс.
Однако в новом
стандарте ГОСТ 21354-87 кривой усталости по контактной прочности для левой
ветви имеет показатель 6, а для правой – 20. Составляющие коэффициента нагрузки
имеют большие значения и приближены к международному стандарту ISO 6336. Тогда
отношение комплексных коэффициентов ![]() будет меньше единицы,
так как
будет меньше единицы,
так как ![]() и
и ![]() . В этой связи установление
отношения комплексных коэффициентов с использованием стандарта ISO 6336 ждет
своего исследователя.
. В этой связи установление
отношения комплексных коэффициентов с использованием стандарта ISO 6336 ждет
своего исследователя.
В заключении
укажем, что на основании исследования В.Н.Кудрявцева установлено, что
одноступенчатый редуктор с передаточным числом u = 10 имеет массу по сравнение
с двухступенчатым на 84% больше, а двухступенчатый редуктор при общем
передаточном числе 63 имеет массу на 34% больше, чем трехступенчатый.
Таким образом,
уменьшение и ограничение передаточных чисел быстроходной ступени
и увеличение числа ступеней передач позволяет не только уменьшить массу, а
также обеспечить конструктивные требования.
Формулу, предложенную
проф. Г.А. Снесаревым для определения передаточных отношений двухступенчатых
редукторов типа Ц2У, можно получить и другим путем - из условия обеспечения
нормальной смазки зубчатых колес, а также уменьшения потерь на разбрызгивание
масел (т.е. барботажные потери). Для этого достаточно принять отношение
диаметров колес тихоходной ступени к быстроходной
равным 1,33 ![]() . Тогда, дополнительно используя общеизвестную зависимость
. Тогда, дополнительно используя общеизвестную зависимость ![]() , получим:
, получим:

Рис.5. Зависимость ![]() от
от
![]() для одноступенчатой цилиндрической передачи
для одноступенчатой цилиндрической передачи

Рис.6. Зависимость ![]() от
от ![]() и
и ![]() для двухступенчатой цилиндрической передачи
для двухступенчатой цилиндрической передачи
при ![]() и
и ![]()

Рис.7. Зависимость ![]() от
от ![]() и
и ![]() для трехступенчатой цилиндрической передачи
для трехступенчатой цилиндрической передачи
при ![]() и
и ![]()
![]() (32)
(32)
![]() (33)
(33)
Данные этих параметров, в зависимости от передаточного числа редуктора, занесены в таблицу 3.
Теоретические основы формул (32) и (33) по Г.А.Снесареву не приводятся, так как не соответствуют стандартам ГОСТ 21354-87 и ISO 6336. Как было указано, является частным случаем РТМ 24.090-76 ВНИИПТМаш для грузоподъемных машин, работающих в повторно – кратковременном режиме.
Исследованием
редукторов типа Ц2У занимались Дунаев П.Ф. и Леликов О.П. Они минимизировали не
только площадь основания корпуса – А,
массы зубчатых колес – МК,
длину редуктора – L и объем редуктора – V в зависимости от отношения передаточных чисел редуктора (uБ/uТ) и
установили влияние его на такие конструктивные ограничения, как диаметр
быстроходного вала под шестерней – df1, расстояние между наружными
кольцами подшипников быстроходной ступени - ![]() и тихоходной -
и тихоходной - ![]() и зазор между колесом
быстроходной ступени и валом колеса тихоходной ступени -
и зазор между колесом
быстроходной ступени и валом колеса тихоходной ступени - ![]() . Для исследования был взят редуктор Т2 = 420 Нм, uред = 20,
. Для исследования был взят редуктор Т2 = 420 Нм, uред = 20, ![]() Н/мм2.
Н/мм2.
Необходимо
подчеркнуть, что такими допускаемыми напряжениями обладают зубчатая пара
средней твердости, т.е. шестерни подвергнутые к
закалке ТВЧ и улучшенные колеса из стали 40Х. При этом считают, что
обеспечивает вышеуказанные требования отношение быстроходной ступени к
тихоходной ![]() Тогда с
использованием общеизвестной зависимости
Тогда с
использованием общеизвестной зависимости ![]() нетрудно получить
формулу для определения передаточных чисел в следующем виде:
нетрудно получить
формулу для определения передаточных чисел в следующем виде:
![]() (34)
(34)
![]() (35)
(35)
Зависимости
межосевого расстояния - ![]() , суммарной массы зубчатых колес – МСК, массы редуктора – МР, диаметра впадин шестерни быстроходной ступени – df
(штрихпунктирная линия), разницы диаметров колес тихоходной ступени по
сравнению с быстроходной
, суммарной массы зубчатых колес – МСК, массы редуктора – МР, диаметра впадин шестерни быстроходной ступени – df
(штрихпунктирная линия), разницы диаметров колес тихоходной ступени по
сравнению с быстроходной ![]() от отношении
передаточного числа быстроходной ступени к тихоходной
– КИ приведены на рис.8.8.
Здесь для сравнения взяты три группы термообработки:
от отношении
передаточного числа быстроходной ступени к тихоходной
– КИ приведены на рис.8.8.
Здесь для сравнения взяты три группы термообработки:
I -
группа- термообработка зубчатых колес - улучшение.
II - группа-термообработка, закалка ТВЧ шестерни, улучшение колеса.
III - группа -
термообработка, цементация шестерни, закалка ТВЧ колес.
Для сравнения и последующего приведения к новым стандартам
составим сводную таблицу 4.
Таблица 4
|
Методика |
Параметры |
up |
|||||||
|
40 |
31,5 |
25 |
20 |
16 |
12,5 |
8 |
|||
|
По Нибергу Н.Я. |
|
11,696 |
9,97 |
8,55 |
7,37 |
6,35 |
5,38 |
4 |
|
|
|
3,42 |
3,16 |
2,9 |
2,7 |
2,5 |
2,3 |
2 |
||
|
|
3,42 |
3,16 |
2,9 |
2,7 |
2,5 |
2,3 |
2 |
||
|
|
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
||
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
По Вольфу В. |
Из графика при с обеспечением |
uБ |
6,6 |
6,3 |
5,15 |
4,25 |
3,84 |
3,25 |
2 |
|
uT |
6 |
5,0 |
4,85 |
4,7 |
4,15 |
3,86 |
4 |
||
|
|
1,1 |
1,09 |
1,06 |
0,90 |
0,88 |
0,84 |
0,5 |
||
|
|
1,77 |
1,78 |
1,69 |
1,70 |
1,63 |
1,61 |
1,66 |
||
|
|
1,75 |
1,80 |
1,67 |
1,74 |
1,66 |
1,67 |
2 |
||
|
По Ниманну Г. |
Из графика при |
uT |
7,1 |
6,3 |
5,6 |
5 |
4 |
3,55 |
2,5 |
|
uБ |
5,6 |
5 |
4,46 |
4 |
4 |
3,52 |
3,2 |
||
|
|
1,26 |
1,26 |
1,25 |
1,25 |
1 |
1 |
0,78 |
||
|
|
1,7 |
1,64 |
1,59 |
1,54 |
1,6 |
1,5 |
1,2 |
||
|
|
1,64 |
1,58 |
1,54 |
1,48 |
1,6 |
1,53 |
1,6 |
||
|
По Ниманну Г. |
Из графика для практики рис.4 |
uT |
8 |
7,1 |
6,5 |
6 |
5,6 |
5,15 |
3,2 |
|
uБ |
5 |
4,4 |
3,8 |
3,3 |
2,25 |
2,43 |
2,5 |
||
|
|
1,6 |
1,6 |
1,7 |
1,8 |
1,96 |
2,1 |
1,28 |
||
|
|
1,57 |
1,49 |
1,43 |
1,36 |
1,30 |
1,25 |
1,33 |
||
|
|
1,47 |
1,39 |
1,3 |
1,22 |
1,24 |
1,06 |
1,25 |
||
|
По Кудряв-цеву В.Н. |
Из графика рис.6 |
uБ |
8,5 |
7,5 |
6,25 |
5,26 |
4,5 |
3,9 |
2,75 |
|
uT |
4,7 |
4,2 |
4,0 |
3,8 |
3,5 |
3,2 |
2,9 |
||
|
Ки |
1,81 |
1,78 |
1,56 |
1,38 |
1,29 |
1,22 |
0,95 |
||
|
Ка |
1,49 |
1,45 |
1,47 |
1,49 |
1,47 |
1,45 |
1,43 |
||
|
Кd |
1,37 |
1,33 |
1,37 |
1,40 |
1,40 |
1,39 |
1,45 |
||
|
По Снесареву Г.А. |
|
8,77 |
7,48 |
6,4 |
5,5 |
4,8 |
4,0 |
3 |
|
|
|
4,56 |
4,2 |
3,9 |
3,6 |
3,3 |
3,1 |
2,7 |
||
|
|
1,92 |
1,77 |
1,64 |
1,52 |
1,42 |
1,3 |
1,13 |
||
|
|
1,46 |
1,45 |
1,44 |
1,43 |
1,42 |
1,42 |
1,37 |
||
|
|
1,33 |
1,33 |
1,33 |
1,33 |
1,33 |
1,33 |
1,33 |
||
|
По Дунаеву П.Ф. |
|
7,18 |
6,4 |
5,7 |
5,1 |
4,5 |
4,0 |
3,2 |
|
|
|
5,57 |
4,9 |
4,4 |
3,9 |
3,5 |
3,1 |
2,5 |
||
|
|
1,30 |
1,30 |
1,30 |
1,30 |
1,30 |
1,30 |
1,30 |
||
|
|
1,70 |
1,60 |
1,50 |
1,49 |
1,39 |
1,34 |
1,24 |
||
|
|
1,64 |
1,56 |
1,50 |
1,45 |
1,39 |
1,34 |
1,24 |
||
|
Для всех по формуле (8.44) |
Ниберг Н.Я. |
11,6 |
10 |
8,6 |
7,4 |
6,4 |
5,4 |
4 |
|
|
Вольф В. |
6,6 |
6,3 |
5,2 |
4,2 |
3,8 |
3,2 |
2 |
||
|
Ниманн Г. |
7,1 |
6,3 |
5,6 |
5,0 |
4,0 |
3,5 |
2,5 |
||
|
Кудрявцев В.Н. |
8,5 |
7,5 |
6,2 |
5,2 |
4,5 |
3,9 |
2,7 |
||
|
Снесарев Г.А. |
8,8 |
7,6 |
6,4 |
5,5 |
4,8 |
4,1 |
3,0 |
||
|
Дунаев П.Ф. |
7,2 |
6,4 |
5,7 |
5,1 |
4,5 |
4,0 |
3,2 |
||
Безусловно,
обеспечение равнопрочности зубчатых передач, подшипников качения, жесткости
валов и общей надежности всей системы - задача очень сложная, при этом
необходимо выдержать такие условия, как ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Если учесть, что на 1 млн. изделий допустимы 6 отказов за планируемый срок службы, то понятны актуальность и важность любого исследования направленного на повышение надежности и вероятности безотказной работы.
Для анализа теоретических и практических данных двухступенчатых передач введем ряд безразмерных параметров, как отношение передаточных чисел – Ки быстроходной ступени – uБ к тихоходной – uТ:
![]() (36)
(36)
Отношение
межцентровых расстояний – Ка
тихоходной ступени - ![]() к
быстроходной -
к
быстроходной - ![]() при КР = 1 будет
при КР = 1 будет
![]() (37)
(37)
Отношение диаметров колес – Кd тихоходной ступени – dKT к быстроходной – dКБ, которое при КР = 1 определяется по выражению
![]() (38)
(38)
Значения новых параметров для сопоставления занесены в таблицу 3.

Рис.8. Зависимости ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() от
от ![]()
Как
видим, по теории Ниберга Н.Я., из условия компактности редуктора (минимального
объема) не обеспечиваются такие конструктивные требования, как жесткость
быстроходного вала (df1 ³
1,25d) и зазор между колесом быстроходной ступени и выходным
валом - ![]() (
(![]() > 30 мм). Поэтому им был установлен предел
применимости для редукторов Ц2У, Ц2 с передаточным
числом от 8 до 20.
> 30 мм). Поэтому им был установлен предел
применимости для редукторов Ц2У, Ц2 с передаточным
числом от 8 до 20.
Немецкий исследователь профессор Вольф В. определил из условия изгибной равнопрочности минимальное суммарное межцентровое расстояние, что важно для стальных твердых зубчатых передач. Из этой теории вытекает параметр Ки, который должен иметь предел 0,84…1,1, при Ка = 1,6…1,8 и Кd = 1,25…1,6. Необходимо отметить, что редукторы 1Ц2у имеют Ка = 1,25…1,6 и по контактной прочности Ки больше указанных пределов до 1,8.
Определением минимального суммарного межцентрового расстояния из условия изгибной прочности занимался профессор Ниманн Г. По его данным Ки = 1…1,25, Ка = 1,5…1,7, Кd = 1,48…1,64. Однако учитывая, что при расчете на контактную прочность зубчатых передач модуль принимается конструктивно и изгибные напряжения получаются намного меньше допускаемого, поэтому для практики нетрудно получить по формулам (8.36; 8.37; 8.38) Ка = 1,25…1,6, Кd = 1,06…1,45 для uР = 8…40, при этом Ки = 2,1…1,6, намного больше Ки = 1,25 (рис. 8.4).
Определением минимальной суммарной массы зубчатых колес из условия
контактной прочности, как было указано раньше, с использованием старого
стандарта ГОСТ 21354-75, занимался профессор Кудрявцев В.Н. При этом Ки = 1,22…1,8, Ка и Кd
почти постоянные величины) ![]() и
и ![]() .
.
Таким образом,
величина зазора между колесом быстроходной ступени и выходным валом – ![]() зависит не только от Ки, но и от Ка.
зависит не только от Ки, но и от Ка.
Как было
указано, исследованием редукторов типа 1Ц2У и 2Ц2 (обозначение
рекомендуемое Снесаревым Г.А.) занимался профессор Снесарев Г.А. При этом для
определения передаточных чисел ступеней выдвинуты два условия Кd = 1,33 для ограниченного срока службы и Кd = 1,11 для не
ограниченного срока службы, поэтому из условия контактной равнопрочности ступеней
при и Крн = 1 для первого случая формулы имеют вид: ![]() и
и ![]() , а для второго случая
, а для второго случая ![]() и
и ![]() . Данные для первого случая сведены в таблицу 8.3, при этом Ка = 1,37…1,46, Кd = 1,33, Ки = 1,13…1,92 для
uР =
8…40. Как видим, по теории Кудрявцева В.Н. и Снесарева Г.А. ограничение Ки = 1, 3 Дунаева П.Ф. и
Леликова О.П. не выдерживается, следовательно, параметрическая оптимизация
многоступенчатых редукторов очень сложна и зависит при прочих равных условиях
от величины крутящего момента.
. Данные для первого случая сведены в таблицу 8.3, при этом Ка = 1,37…1,46, Кd = 1,33, Ки = 1,13…1,92 для
uР =
8…40. Как видим, по теории Кудрявцева В.Н. и Снесарева Г.А. ограничение Ки = 1, 3 Дунаева П.Ф. и
Леликова О.П. не выдерживается, следовательно, параметрическая оптимизация
многоступенчатых редукторов очень сложна и зависит при прочих равных условиях
от величины крутящего момента.
В исследованиях Дунаева П.Ф. и Леликова О.П. для определения передаточных чисел ступеней редукторов типа Ц2У и Ц2 по развернутой схеме были получены Ки = 1,3 для частного случая при uР = 20 для обеспечения минимальной суммарной массы зубчатых колес и конструктивных ограничений.
Действительно,
по теории Кудрявцева В.Н. при Ки
= 1,38 и uР = 20 обеспечивается минимальная масса
зубчатых колес. Однако с изменением передаточного числа редуктора для uР
= 8…40, отношение передаточных чисел ступеней изменяется от 1,22 до 1,81, что
вытекает из графика Ниманна Г. при обеспечении изгибной прочности зубьев
ступеней.
В новом
учебнике по конструированию узлов и деталей Ки
= 1,3 рекомендуется для обеспечения разницы радиусов колес ступеней – ![]() >30
мм, где указывается, что это необходимо для уменьшения потерь на разбрызгивание
масла.
>30
мм, где указывается, что это необходимо для уменьшения потерь на разбрызгивание
масла.
В заключении отметим, что профессор Ниманн Г., понимая сложность рассматриваемой проблемы для определения передаточных чисел ступеней редукторов типа Ц2У и Ц3У, предложил графическую зависимость (рис.4).
Как известно, межосевое расстояние, определенное из контактной прочности, намного больше, чем по изгибным напряжениям зубчатой передачи, поэтому Ниманн Г. установил верхнюю и нижнюю границу передаточного числа быстроходной ступени для редукторов Ц2У, где пунктирная линия для твердых зубчатых передач, которая параллельна штрихпунктирной линии, полученной из теории по изгибной прочности. Для зубчатых передач мягкой твердости передаточное число быстроходной ступени больше и к теоретическому положению имеет некоторый наклон. Графическая зависимость приводится также в учебнике профессора Иванова М.Н. по деталям машин.
Следует подчеркнуть, что вышеизложенная параметрическая оптимизация проведена на основе старого стандарта, где правая ветвь кривой выносливости Вёлера параллельна оси абсцисс.
На основе нового стандарта ГОСТ 21354-87, для теоретического положения Ниберга Н.Я. можно получить следующие формулы:
Передаточное число быстроходной ступени
![]() ;
(39)
;
(39)
Передаточное число тихоходной
ступени
![]() ;
(40)
;
(40)
Отношение передаточных чисел
ступеней
![]() ; (41)
; (41)
Отношение межцентровых расстояний
![]() ; (42)
; (42)
Отношение диаметров колес
![]() ; (43)
; (43)
Как видно, по приведенным формулам (39 – 43) определить параметры проектируемого редуктора невозможно, так как неизвестен коэффициент нагруженности редуктора (и желаемой долговечности) – КР. С другой стороны задача может быть решена методом последовательных приближений (итераций).
На основе анализа существующих конструкций редукторов 1Ц2У, можно обнаружить следующее: во – первых, с крутящим моментом на выходе до 10 тысяч Нм редукторы имеют передаточное число до 41, а при крутящем моменте свыше 10 тысяч Нм общее передаточное число доходит до 50. Следовательно, конструктивные ограничения косвенно зависят также от величины крутящего момента. Таким образом, применение врезной вал – шестерни для быстроходной ступени возможно при значительном крутящем моменте.
Произведение
коэффициента нагруженности редуктора – КРН
на отношение межцентровых расстоянии приближенно
составляет ![]() тогда передаточное
отношение быстроходной ступени будет
тогда передаточное
отношение быстроходной ступени будет
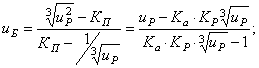 (44)
(44)
Для
определения передаточного числа тихоходной ступени и отношения передаточных
чисел редуктора можно использовать общеизвестную зависимость ![]() и
и ![]()
Отношение межцентровых расстояний определяется по формуле (42), а диаметров колес – по формуле (43).
Как было указано раньше коэффициент нагруженности редуктора по изгибной прочности
![]()
Учитывая данное обстоятельство Ниманном получено ![]() тогда передаточное
число быстроходной ступени будет
тогда передаточное
число быстроходной ступени будет
![]() (45)
(45)
Передаточное
число тихоходной ступени будет
![]() (46)
(46)
Отношение
межосевых расстояний:
![]() (47)
(47)
Отношение
диаметров колес
![]() (48)
(48)
Отношение
передаточных чисел ступеней
![]()
Для сравнения различных методик расчета на основе нового стандарта составили новую таблицу 5.
По новому стандарту ГОСТ 21354-87 и ISO 6336 коэффициент нагруженности редуктора по контактной прочности – КрН изменяется от 1,2 до 1,3 при uP = 8…48, а коэффициент нагруженности редуктора по изгибной прочности KpF = 0,98…0,96.
Выводы и рекомендации
По теории Ниманна Г. изгибная прочность зубьев обеспечивается при u = 8…16 Ки = 1; при uP = 20…40 Ки = 1,25; при uP = 40…50 Ки = 1,3.
При заданном отношении передаточных чисел ступеней Ки = 1,25 из условия равнопрочности зубьев по изгибу первоочередной задачей является обеспечение контактной прочности ступеней.
Одновременная минимизация всех параметров невозможна, но создание равнопрочной конструкции редуктора возможно.
Таблица 5
|
Параметры |
uP |
||||
|
40 |
20 |
12,5 |
10 |
||
|
По Нибергу Н.Я. |
|
1,27 |
1,26 |
1,22 |
1,22 |
|
|
9,2 |
5,8 |
4,4 |
3,8 |
|
|
|
4,3 |
3,4 |
2,8 |
2,6 |
|
|
|
2,1 |
1,7 |
1,5 |
1,44 |
|
|
|
По формуле (42) |
1,1 |
1,1 |
1,1 |
1,1 |
|
|
1 |
1 |
1 |
1 |
|
|
По Снесареву Г.А. |
|
8,3 |
5,2 |
4,0 |
3,0 |
|
|
4,8 |
3,8 |
3,1 |
2,7 |
|
|
|
1,71 |
1,36 |
1,29 |
1,12 |
|
|
|
1,2 |
1,2 |
1,17 |
1,13 |
|
|
|
1,11 |
1,11 |
1,11 |
1,11 |
|
|
Предлагаемый метод |
|
1,6 |
1,4 |
1,3 |
1,25 |
|
|
7,1 |
5 |
4 |
3,55 |
|
|
|
5,6 |
4 |
3,15 |
2,8 |
|
|
|
1,26 |
1,25 |
1,27 |
1,27 |
|
|
|
1,34 |
1,22 |
1,18 |
1,15 |
|
|
|
1,29 |
1,17 |
1,12 |
1,06 |
|
|
По Ниманну Г. |
|
7,1 |
5,0 |
4,0 |
3,55 |
|
|
5,6 |
4 |
3,1 |
2,8 |
|
|
|
1,25 |
1,25 |
1,25 |
1,25 |
|
|
|
1,34 |
1,22 |
1,18 |
1,15 |
|
|
|
1,29 |
1,17 |
1,12 |
1,06 |
|
4. Для многоступенчатых цилиндрических передач требуется проведение обширного исследования по развернутой схеме на основе нового стандарта из условия изгибной и контактной равнопрочности с использованием метода Лагранжа.
5.Для редукторов типа Ц2У и Ц2 как по старому, так и по новому стандартам, определение передаточного числа быстроходной ступени производится по формуле:

Проектный расчет двухступенчатого соосного редуктора типа
Ц2С
Редукторы Ц2С выпускаются в виде отдельного агрегата и мотор – редуктора. При этом затраты на изготовление редуктора и стоимость электродвигателя составляют свыше 80 % от всей стоимости привода, а на изготовление рамы, муфты и других деталей расходуется менее 20% средств. В этой связи повышение срока службы редуктора с обеспечением равнопрочности всех деталей является актуальной задачей.
При
конструировании редуктора наилучшим образом должны быть выбраны оптимальные
параметры, удовлетворяющие различным требованиям: наименьшей массе зубчатых
колес и самого редуктора, стоимости, компактности, равнопрочности элементов,
ограничений максимального передаточного отношения быстроходной ступени для
обеспечения условии ![]() , нормальной смазки подшипников, минимальных потерь на
разбрызгивание масла и т.д.
, нормальной смазки подшипников, минимальных потерь на
разбрызгивание масла и т.д.
Цель работы – проведение оптимизации параметров редуктора 1Ц2С без выполнения эскизной компоновки, необходимой при обеспечении конструктивных ограничений. Это даст возможность для широкого внедрения систему автоматизированного проектирования (САПР).
В связи с появлением новых международного и российского стандартов, может быть введено отношение нагруженности и контактных напряжений ступеней. Его следует рассматривать, как отношение комплексных коэффициентов контактных напряжений ступеней, введенное профессором В.Н. Кудрявцевым при выполнении зубчатых колес из стали.
Для краткости отношения комплексных коэффициентов вводится отношение нагруженности ступеней и оно имеет вид:
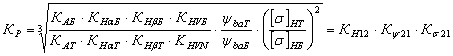 (49)
(49)
где  - отношение коэффициентов нагрузок быстроходной ступени к
тихоходной;
- отношение коэффициентов нагрузок быстроходной ступени к
тихоходной; 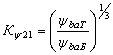 - отношение коэффициентов ширины относительно межцентровых
расстояний тихоходной ступени к быстроходной;
- отношение коэффициентов ширины относительно межцентровых
расстояний тихоходной ступени к быстроходной; ![]() - отношение допускаемых напряжений тихоходной ступени к быстроходной; КАБ
= КАТ -
коэффициенты внешней динамики ступеней.
- отношение допускаемых напряжений тихоходной ступени к быстроходной; КАБ
= КАТ -
коэффициенты внешней динамики ступеней.
Тогда при равенстве межцентровых расстояний для двухступенчатого соосного редуктора даст следующую зависимость:
![]() (50)
(50)
Совместное решение
с общеизвестным уравнением ![]() даст формулу для определения передаточного числа быстроходной
ступени с внешним зацеплением
даст формулу для определения передаточного числа быстроходной
ступени с внешним зацеплением
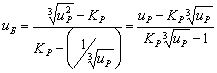 ;
(51)
;
(51)
Эта формула имеет вид, как для редуктора Ц2У при Ка=1. Следовательно, между двухступенчатыми цилиндрическими редукторами по развернутой схеме и соосной с внешним зацеплением существует взаимосвязь, и можно использовать существующие теории для развернутой схемы.
Для сравнения различных теорий введем следующие относительные параметры:
Отношение
передаточных чисел быстроходной ступени – uБ к
тихоходной – uТ.
![]()
С этим параметром связана изгибная прочность
зубьев колес всех ступеней. Оптимальные отношения, по исследованиям немецких ученых Г. Ниманна и
В. Вольфа, находятся в пределах 1,1…1,3.
По исследованиям Дунаева П.Ф. и Леликова О.П. с
отношением передаточных чисел ступеней также связана минимальная суммарная
масса зубчатых колес и конструктивные ограничения.
Второй параметр - отношение диаметров колес
тихоходной ступени к быстроходной, от которого зависит
объем редуктора и необходимая высота погружения зубчатых колес в масляную
ванну. Отношение диаметров колес через
межцентровое расстояние дает уравнение:
 (52)
(52)
Эта формула при КР = 1 дает равенство диаметров при ![]() и
и ![]() Таким образом, при КР>1 отношение диаметров будет меньше единицы.
Таким образом, при КР>1 отношение диаметров будет меньше единицы.
Отношение
действительной ширины контакта зубчатых колес тихоходной ступени – bТ к быстроходной – bБ можно получить из равенства межцентровых
расстояний ![]() которое дает
выражение:
которое дает
выражение:
 (53)
(53)
Данное
выражение дает возможность обеспечить контактную равнопрочность ступеней, т.е.![]() и
и ![]() .
.
Коэффициент
ширины для тихоходной ступени редукторов типа 1Ц2С рекомендуется ![]() = 0,315…0,4 при использовании улучшенных зубчатых колес, а
= 0,315…0,4 при использовании улучшенных зубчатых колес, а ![]() = 0,25…0,315 из закаленных
сталей.
= 0,25…0,315 из закаленных
сталей.
Коэффициент ширины
быстроходной ступени лучших мировых образцов редукторов типа 1Ц2С
связаны следующим соотношением ![]() .
.
Определение
передаточных чисел ступеней из условия равенства межцентровых расстоянии с использованием ![]() дает сложное уравнение со многими переменными. Графическая
зависимость передаточного числа быстроходной ступени от общего передаточного
числа редуктора типа Ц2С при различном значении комплексного коэффициента –
дает сложное уравнение со многими переменными. Графическая
зависимость передаточного числа быстроходной ступени от общего передаточного
числа редуктора типа Ц2С при различном значении комплексного коэффициента – ![]() приведена в учебнике
по курсовому проектированию.
приведена в учебнике
по курсовому проектированию.
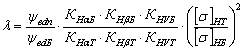
При ![]() = 3 передаточное число ступеней в пределах uP
= 12,5…20 равны, а при uP
= 8 передаточное число
быстроходной ступени меньше тихоходного, что не соответствует реальности. При
= 3 передаточное число ступеней в пределах uP
= 12,5…20 равны, а при uP
= 8 передаточное число
быстроходной ступени меньше тихоходного, что не соответствует реальности. При ![]() = 1 передаточное число
быстроходной ступени превышает uБ =
8 уже при uP
= 25 и выше. Следовательно, комплексный коэффициент –
= 1 передаточное число
быстроходной ступени превышает uБ =
8 уже при uP
= 25 и выше. Следовательно, комплексный коэффициент – ![]() имеет сложную
зависимость от передаточного числа редуктора.
имеет сложную
зависимость от передаточного числа редуктора.
В работах
Ниберга Н.Я. приняты ![]() что является частным
случаем, во – вторых, сокращение
что является частным
случаем, во – вторых, сокращение ![]() принимается с большим
допущением и с учетом этих обстоятельств получена зависимость:
принимается с большим
допущением и с учетом этих обстоятельств получена зависимость:
![]()
Для решения этого
уравнения на ЭВМ предлагается определить ![]() где
где![]() и
и 
Предлагаемая
зависимость требует использования ЭВМ и рекомендуемые значения С приведены в
таблице. Анализ табл. 4. показывает, что отношение передаточных чисел - КИ быстроходной ступени – uБ к тихоходной – uТ получается постоянным, равным двум. Это дает
простое решение для определения передаточных чисел ступеней ![]() и
и ![]() , что гораздо проще
для вычисления, чем использование вышеприведенной
сложной зависимости.
, что гораздо проще
для вычисления, чем использование вышеприведенной
сложной зависимости.
Формулы для
определения передаточных чисел ступеней, предлагаемые Дунаевым П.Ф. и Леликовым
О.П., получены из выражений ![]() и
и ![]() . Совместное решение этих простых зависимостей дает формулу
для нахождения передаточного числа быстроходной ступени
. Совместное решение этих простых зависимостей дает формулу
для нахождения передаточного числа быстроходной ступени
![]() (54)
(54)
Передаточное
число тихоходной ступени в зависимости от общего передаточного числа редуктора
- uP имеет вид.
![]() (55)
(55)
Приведенные
формулы дают удовлетворительные практические результаты, несмотря на отсутствие
глубокого теоретического обоснования.
Формула для
определения передаточного числа быстроходной ступени, предлагаемая профессором
Г.А. Снесаревым, имеет аналитический вывод
![]() (56)
(56)
Как видим из данной формулы отношение нагруженности для всего диапазона
передаточных чисел редуктора является
постоянной величиной.
В заключении отметим, что отношения нагруженности можно получить из
диаметров колес ступеней
 (57)
(57)
С другой
стороны для определения передаточного числа быстроходной ступени имеет выражение (51) и после подстановки в выражение (57)
получим предельное значение
отношения нагруженности.
![]() (58)
(58)
Следовательно, все три составляющие отношения нагруженности зависят от общего передаточного числа редуктора.
Отношение коэффициента нагрузок КН12 зависит от многих факторов и из практических расчетов можно получить следующую приближенную зависимость
![]() (59)
(59)
здесь КАБ = КАТ - коэффициент
внешней динамики ступеней.
Следующие
отношения ![]() и
и ![]() это инструмент для выравнивания при расчете и
конструировании. Если считать оптимальным
это инструмент для выравнивания при расчете и
конструировании. Если считать оптимальным ![]() , то произведение
, то произведение ![]() и
и ![]() составляет
составляет ![]() .
.
Отношение
допускаемых напряжений ступеней при одинаковых материалах и термообработке
шестерен, а также при аналогичных условиях для колес ступеней можно получить
следующее выражение:
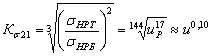 (60)
(60)
Тогда
отношение коэффициентов ширины
![]() (61)
(61)
Результаты
определения параметров редуктора типа 1Ц2С по формулам различных авторов
приведены в таблице 6.
Таким образом,
для определения передаточного числа быстроходной ступени на этапе проектирования
предлагается выражение
![]() (62)
(62)
Отношение
коэффициентов ширины будет
 (63)
(63)
Отношение
диаметров колес находим по уточненной формуле
 (64)
(64)
Таблица 6
|
uP |
40 |
31,5 |
25 |
20 |
16 |
12,5 |
10 |
8 |
|
|
Параметры |
|||||||||
|
По Нибергу Н.Я |
С |
- |
- |
15,8 |
12,9 |
10,7 |
9,0 |
7,61 |
6,37 |
|
|
- |
- |
7,1 |
6,3 |
5,6 |
5,0 |
4,5 |
4,0 |
|
|
|
- |
- |
3,55 |
3,15 |
2,8 |
2,5 |
2,24 |
2 |
|
|
|
- |
- |
2 |
2 |
2 |
2 |
2 |
2 |
|
|
|
- |
- |
1,20 |
1,19 |
1,19 |
1,19 |
1,19 |
1,18 |
|
|
|
- |
- |
0,98 |
0,96 |
0,94 |
0,90 |
0,85 |
0,8 |
|
|
По Дунаеву П.Ф. |
|
7,1 |
6,3 |
5,6 |
5,0 |
4,5 |
4,0 |
3,55 |
3,15 |
|
|
5,6 |
5,0 |
4,5 |
4,0 |
3,55 |
3,15 |
2,8 |
2,5 |
|
|
|
1,23 |
1,23 |
1,23 |
1,23 |
1,23 |
1,23 |
1,23 |
1,23 |
|
|
По Снесареву Г.А.. |
|
9,4 |
8 |
7 |
5,8 |
5 |
4,2 |
3,5 |
2,9 |
|
|
4,25 |
3,9 |
3,6 |
3,4 |
3,2 |
3,3 |
2,8 |
2,70 |
|
|
|
2,2 |
2 |
1,96 |
1,7 |
1,6 |
1,3 |
1,25 |
1,1 |
|
|
|
1,25 |
1,2 |
1,23 |
1,25 |
1,24 |
1,3 |
1,24 |
1,246 |
|
|
|
1,12 |
1,11 |
1,1 |
1 |
1,14 |
0,81 |
1,2 |
1,22 |
|
|
Предлагаемая методика |
|
7,1 |
6,3 |
5,6 |
5,0 |
4,5 |
4,0 |
3,55 |
3,15 |
|
|
5,6 |
5,0 |
4,5 |
4,0 |
3,55 |
3,15 |
2,8 |
2,5 |
|
|
|
1,08 |
1,09 |
1,08 |
1,07 |
1,06 |
1,05 |
1,04 |
1 |
|
|
|
0,95 |
0,94 |
0,94 |
0,94 |
0,93 |
0,93 |
0,92 |
0,91 |
|
|
|
1,25 |
1,26 |
1,24 |
1,25 |
1,26 |
1,27 |
1,27 |
1,12 |
|
Выводы и рекомендации
1. Обеспечение максимального наименьшего объема редуктора не может быть самоцелью, если не обеспечены контактные и изгибные равнопрочности зубьев колес.
2. Предложенные формулы должны обеспечить конструктивные ограничения без выполнения эскизной компоновки.
3. Отношение нагруженности и его составляющие зависят от общего передаточного числа редуктора.
Проектный расчет двухступенчатого коническо –
цилиндрического редуктора типа кц 1
Редукторы КЦ1 и КЦ2, КДВ выпускались в качестве отдельного агрегата, для привода консольно-поворотных кранов, пластинчатых и подвесных конвейеров, а также ряда других машин.
Следует указать, что в Германии выпускаются цилиндро – конические редукторы типа Ц1К и Ц2К для привода конвейеров.
При конструировании к ним предъявляются те же требования,что и для редукторов типа Ц 2У, Ц3У и Ц2С.
Как было указано раннее, в последние годы в России появились коническо – цилиндрические мотор – редукторы с вертикальным расположением вала конической шестерни, что намного уменьшает длину привода.
Необходимо отметить, что конические передачи с круговыми зубьями не уступают по несущей способности гипоидной зубчатой передаче, поэтому нашли широкое применение в главных передачах плавающих тягачей и многоприводных подвесных грузотолкающих конвейерах с развернутой длиной 3 км и более. Разработаны новые конструкции подшипниковых узлов конической вал - шестерни. Диаметр конического колеса по торцу определяется по формуле:
 (65)
(65)
где ![]() - расчетный момент на колесе в нм.
- расчетный момент на колесе в нм.
Диаметр делительной окружности цилиндрического колеса тихоходной ступени из условия контактной прочности имеет вид:
 (66)
(66)
здесь ![]() - расчетный момент на шестерне в нм.
- расчетный момент на шестерне в нм.
Приравнивание диаметров конического и цилиндрического колес даст выражение:
![]() (67)
(67)
где
 - отношение
нагруженности коническо – цилиндрической передачи.
- отношение
нагруженности коническо – цилиндрической передачи.
Совместное
решение уравнения (67) и зависимости ![]() дает
дает
![]() , здесь
, здесь ![]()
тогда
![]() (68)
(68)
Неполное
кубическое уравнение приводится в виде:
![]() (68а)
(68а)
здесь
коэффициенты ![]() ;
; ![]() .
.
Корни ![]() ,
, ![]() ,
, ![]() неполного кубического
уравнения равны
неполного кубического
уравнения равны![]()
![]() ;
; ![]() ;
;
где ![]() ;
; ![]()
![]() ; причем в качестве
; причем в качестве ![]() и
и ![]() берутся
любые значения кубических корней из соответствующих комплексных чисел,
удовлетворяющих соотношению
берутся
любые значения кубических корней из соответствующих комплексных чисел,
удовлетворяющих соотношению ![]() .
.
Значение коэффициентов “а” и “в”, в зависимости
от термообработки приведены в таблице 7.
Таблица 7
|
Группа термообработки |
I |
II |
III-IV |
|
Параметры |
|||
|
а |
1,22 |
1,13 |
0,81 |
|
в |
0,21 |
0,13 |
0,15 |
|
Характеристики зубчатой пары по твердости |
мягкие |
средней твердости |
твердые |
Решение неполного кубического
уравнения для случая ![]() ,
, ![]() ,
, ![]() , тогда коэффициенты
, тогда коэффициенты ![]() ;
; ![]() ;
;
Уравнение имеет вид
![]()
Коэффициенты, выраженные через ![]() будут
будут
![]()
![]()
![]()
Действительный корень
уравнения ![]() ;
; ![]() положительно при
положительно при ![]()
Приближенное решение корня имеет
вид:
![]() (69)
(69)
Передаточное число конической зубчатой пары в
зависимости от общего передаточного числа редуктора приведен
в таблице 8.
Таблица 8
|
|
28 |
20 |
14 |
10 |
6,3 |
|
|
6,3 4,5 |
5,0 4,0 |
4 3,55 |
3,55 2,8 |
2,8 2,24 |
|
где |
6,3 4,5 |
5,0 4,0 |
3,55 4 |
3,15 3,15 |
2,24 2,8 |
|
|
5 5,6 |
4,0 5,0 |
3,55 4 |
2,8 3,55 |
2,24 2,8 |
|
|
5 5,6 |
4,2 4,6 |
4 3,55 |
3,15 3,15 |
3,15 2,4 |
|
|
5 5,6 |
4,0 5,0 |
3,55 4 |
2,8 3,55 |
2,24 2,8 |
|
Рекомендуемые Заводом-изготовителем
|
6,3 5,6 |
5,0 4,0 |
4 3,55 |
3,15 3,15 |
3,15 2,4 |
Графическая
зависимость передаточного числа быстроходной конической пары от общего
передаточного редуктора, предложенная Ивановым М.Н. и Ивановым В.Н., при различных
значениях ![]() приведена в таблице
8.7. Как видим, минимальный объем
редуктора сохраняется при
приведена в таблице
8.7. Как видим, минимальный объем
редуктора сохраняется при ![]() .
.
Дунаевым П.Д.
и Леликовым О.П. предложенные формулы получены
при ![]() Обоснование приведенного
соотношения не приводится, однако не трудно догадаться, что здесь учтен ограничения
Обоснование приведенного
соотношения не приводится, однако не трудно догадаться, что здесь учтен ограничения ![]() и
и ![]()
![]()
В методических
указаниях по расчету зубчатых передач кафедры детали машин МГТУ им. Н.Э. Баумана
для определения передаточных чисел рекомендуются зависимости ![]() и
и ![]() .
.
Формулы,
предложенные проф. Снесаревым Г.А., для определения передаточного числа
тихоходной ступени, не имеют универсальности, так
например:
![]() при
при ![]()
![]() при
при ![]()
где  - коэффициент
долговечности.
- коэффициент
долговечности.
Необходимо
отметить, что в редукторах старой конструкции КЦ1,если
передаточное число конической пары было постоянное ![]() , то в новых конструкциях рекомендуемое число приведено в
таблице. Считаем достаточно необоснованным ограничение
конической пары
, то в новых конструкциях рекомендуемое число приведено в
таблице. Считаем достаточно необоснованным ограничение
конической пары ![]() , так как в транспортных машинах, например, в главной передаче гусеничных
плавающих вездеходов
, так как в транспортных машинах, например, в главной передаче гусеничных
плавающих вездеходов ![]() . Поэтому для теоретического исследования предельным
значением следует считать
. Поэтому для теоретического исследования предельным
значением следует считать ![]() .
.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов