Главная

Содержание

2. Расчет зубчатых передач

2.1. Порядок расчета зубчатых передач

2.2. Выбор материала зубчатых колес и вида термообработки

2.3. Расчет допускаемых напряжений

2.4. Проектный расчёт закрытой цилиндрической зубчатой передачи

2.5. Геометрический расчёт закрытой цилиндрической передачи

2.6. Проверочный расчёт закрытой цилиндрической передачи

2.7. Расчёт открытой цилиндрической зубчатой передачи

2.8. Расчёт закрытой конической зубчатой передачи

2.9. Проектный расчёт открытой конической прямозубой передачи

2.10. Конструирование зубчатых колес

2. Расчет зубчатых передач

2.1. Порядок расчета зубчатых передач

1. Порядок расчета цилиндрической прямозубой передачи

Проектировочный расчет закрытой передачи

1.1. Выбор материала зубчатых колес и определение допускаемого контактного напряжения

1.2. Определение межосевого расстояния из условия контактной выносливости активных поверхностей зубьев

1.3. Назначение модуля передачи

1.4. Определение чисел зубьев шестерни и колеса

1.5. Уточнение передаточного числа

1.6. Определение основных геометрических размеров шестерни и колеса, уточнение

Проверка зубьев на выносливость по контактным напряжениям

1.7. Определение коэффициентов концентрации и динамичности нагрузки

1.8. Определение расчетных контактных напряжений

1.9. Сопоставление расчетного и допускаемого напряжений

Проверка зубьев на выносливость по напряжениям изгиба

1.10. Определение усилий в зацеплении

1.11. Определение допускаемого изгибного напряжения

1.12. Определение коэффициентов концентрации и динамичности нагрузки

1.13. Определение расчетных напряжений изгиба

1.14. Сопоставление расчетных и допускаемых напряжений

Расчет шестерни открытой передачи

1.15. Выбор материала шестерни и определение допускаемого изгибного напряжения

1.16. Определение модуля передачи

1.17. Определение основных размеров шестерни

1.18. Проверка зубьев на изгибную прочность

2. Порядок расчета цилиндрической косозубой передачи

Проектировочный расчет закрытой передачи

2.1. Выбор материала колес и определение допускаемого контактного напряжения

2.2. Определение межосевого расстояния

2.3. Назначение нормального модуля передачи.

2.4. Назначение угла наклона зубьев (в пределах 8…20°)

2.5. Определение чисел зубьев колеса и шестерни

2.6. Уточнение передаточного числа

2.7. Уточнение угла наклона зубьев

2.8. Определение основных геометрических размеров колес

Проверка зубьев на выносливость по контактным напряжениям

2.9. Определение коэффициентов концентрации и динамичности нагрузки

2.10. Определение расчетных контактных напряжений

2.11. Сопоставление расчетного и допускаемого напряжений

Проверка зубьев на изгибную прочность

2.12. Определение усилий в зацеплении

2.13. Определение допускаемого напряжения изгиба

2.14. Определение коэффициентов концентрации и динамичности нагрузки

2.15. Определение расчетных напряжений изгиба и сопоставление их с допускаемыми значениями

3. Порядок расчета шевронных передач

Проектировочный расчет передачи

3.1. Выбор материала колес и определение допускаемых напряжений

3.2. Определение межосевого расстояния с округлением до стандартного значения по ряду Ra 40

3.3. Определение модуля зацепления с округлением до стандартного

3.4. Определение числа зубьев колес

3.5. Уточнение угла наклона зубьев и передаточного числа

3.6. Определение геометрических размеров колес

Проверочный расчет передачи

3.7. Определение коэффициента распределения нагрузки между зубьями и коэффициентов нагрузки

3.8. Проверка зубьев на выносливость по контактным напряжениям

3.9. Проверка зубьев на выносливость при изгибе

4. Порядок расчета зубчатых передач с коническими прямозубыми колесами

Проектировочный расчет закрытой конической передачи

4.1. Выбор материала зубчатых колес и определение допускаемых контактных и изгибных напряжений

4.2. Определение диаметра внешней делительной окружности колеса d_e2.

4.3. Определение числа зубьев шестерни и колеса (для цементированных конических передач при мм числа зубьев шестерни ориентировочно можно принять равными 18…25 при u = 2,5; 16…18 при и 15…16 при u = 6). Для передач с термоулучшенными колесами значения можно увеличить на 10...20% (против указанных величин)

4.4. Уточнение передаточного числа

4.5. Определение основных геометрических параметров зубчатого колеса и шестерни (рекомендуется оформлять в виде таблицы)

Проверка зубьев на выносливость по контактным напряжениям

4.6. Определение окружной скорости колес

4.7. Определение коэффициентов концентрации и динамичности нагрузки и

4.8. Определение расчетных контактных напряжений

4.9. Сопоставление расчетного и допускаемого напряжений

Проверка зубьев на выносливость по напряжениям изгиба

4.10. Определение эквивалентного числа зубьев, коэффициентов, учитывающих форму зуба для шестерни и колеса –

4.11. Определение коэффициентов концентрации и динамичности нагрузки и

4.12. Определение расчетных напряжений изгиба

4.13. Сопоставление расчетных и допускаемых напряжений

Проектировочный расчет шестерни открытой конической передачи

4.14. Выбор материала и определение допускаемого напряжения изгиба шестерни

4.15. Определение среднего модуля из условия выносливости зубьев по напряжениям изгиба

4.16. Определение внешнего окружного модуля

4.17. Расчет основных геометрических параметров шестерни (рекомендуется результаты расчета свести в таблицу)

Проверка зубьев шестерни на выносливость по напряжениям изгиба

4.18. Определение и шестерни

4.19. Определение коэффициентов и

4.20. Определение расчетных напряжений изгиба

4.21. Сопоставление расчетных и допускаемых напряжений

2.2. Выбор материала зубчатых колес и вида термообработки

При выборе материала зубчатых колес следует учитывать назначение проектируемой передачи, условия эксплуатации, требования к габаритным размерам и возможную технологию изготовления колёс. Основным материалом для изготовления зубчатых колёс является сталь. Необходимую твердость в сочетании с другими механическими характеристиками (а следовательно, желаемые габариты и массу передачи) можно получить за счет назначения соответствующей термической или химико-термической обработки стали.

В условиях индивидуального и мелкосерийного производства, в мало- и средненагруженных передачах, а также в передачах с большими габаритами колес (когда термическая обработка их затруднена) обычно применяют стали с твердостью не более 350 НВ, которая обеспечивается нормализацией или термоулучшением материала. При этом возможно чистовое нарезание зубьев непосредственно после термообработки с высокой точностью изготовления, а при работе передачи обеспечивается хорошая прирабатываемость зубьев без хрупкого разрушения их при динамических нагрузках.

Для равномерного изнашивания зубьев и лучшей их прирабатываемости твёрдость шестерни НВ₁ рекомендуют назначать больше твёрдости НВ₂ колеса не менее чем на (10…15) НВ.

В условиях крупносерийного и массового производства целесообразно применять зубчатые колеса с высокотвердыми зубьями. При твердости более 350 НВ её обычно выражают в единицах Роквелла − НRC (1 HRC = 10 НВ).

Такая твердость обеспечивается после проведения упрочняющих видов термической и химикотермической обработки: закалки (обьемной или поверхностной), цементации с последующей закалкой, азотирования и др.

Применение высокотвердых материалов является резервом повышения нагрузочной способности зубчатых передач, уменьшения их габаритов и массы. Однако с высокой твердостью материала связаны дополнительные трудности: плохая прирабатываемость зубьев, прогрессирующее усталостное выкрашивание рабочих поверхностей зубьев, необходимость проведения термообработки после зубонарезания. Большинство видов упрочняющей термообработки сопровождается значительным короблением зубьев. Для исправления формы зубьев, восстановления требуемой степени точности требуются дополнительные дорогостоящие зубоотделочные операции (шлифование, полирование, притирка и т.п.), что удлиняет технологический процесс изготовления зубчатых колес и значительно повышает стоимость передачи.

Рекомендуемые для изготовления зубчатых колес марки конструкционных сталей, виды их термообработки и соответствующие основные механические характеристики приведены в табл. 2.1. При этом важно, чтобы размеры заготовок колес (диаметр D_заг и толщина обода или диска S_заг) не превышали предельных значений D_пред и S_пред .

Таблица 2.1. Механические характеристики сталей

Марка стали	Dпред, мм	Sпред, мм	Термооб работка	Твёрдость заготовки
				поверхности	сердцевины	Н/мм^2
1	2	3	4	5	6	7	8		9
35	−	−	Н	163...192 НВ		550	270		235
40	120	60	У	192...228 НВ		700	400		300
45	−	−	Н	179...207 НВ		600	320		260
45	125	80	У	235...262 НВ		780	540		335
45	80	50	У	269...302 НВ		890	650		380
40Х	200	135	У	235...262 НВ		790	640		375
40Х	125	80	У	269...302 НВ		900	750		410
40Х	125	80	У+ТВЧ	45...50 НRCэ	269...302 НВ	900	750		410
40ХН	315	200	У	235...262 НВ		800	630		380
40ХН	200	125	У	269...302 НВ		920	750		420
40ХН	200	125	У+ТВЧ	48...53 НRCэ	269...302 НВ	920	750		420
35ХМ	315	200	У	235...262 НВ		800	670		380
35ХМ	200	125	У	269...302 НВ		920	790		420
35ХМ	200	125	У+ТВЧ	48...53 НRCэ	269...302 НВ	920	790		420
35Л	−	−	Н	163...207 НВ		550	270		235
40Л	−	−	Н	147 НВ		520	295		225
45Л	315	200	У	207...235 НВ		680	440		285
40ГЛ	315	200	У	235...262 НВ		850	600		365
20Х 18ХГТ 12ХН3А	200	125	У+ЦК	56...63 НRCэ	300...400 НВ	900	800		400
38ХМЮА	−	−	А	57...67 НRCэ	30...35 НRC	1050	900		500
35ХМ 40ХН	−	40	З	45...53 НRC		1060	1400		500

Примечания:

1. В графе "Термообработка" приняты следующие обозначения:

Н −нормализация, У −улучшение, ТВЧ −закалка токами высокой частоты, З –объемная закалка, ЦК –цементация, А − азотирование.

2. Для цилиндрических и конических колёс с выточками принять меньшее из значений D_заг, S_заг.

2.3. Расчет допускаемых напряжений

Допускаемые контактные напряжения

Расчет на усталость рабочих поверхностей зубьев колес при циклических контактных напряжениях базируется на экспериментальных кривых усталости, которые обычно строят в полулогарифмических координатах (рис. 2.1).

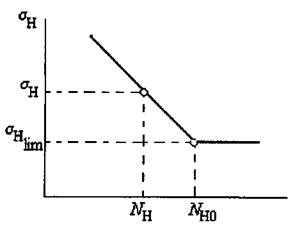
Рис. 2.1

Здесь: − наибольшее напряжение цикла, N_H − число циклов нагружений, − предел выносливости материала, N_HG(N_H0) − базовое число циклов (абсцисса точки перелома кривой усталости).

Допускаемое контактное напряжение рассчитывают для каждого зубчатого колеса передачи по формуле

где определяют по эмпирическим зависимостям, указанным в табл.2.2;

− коэффициент безопасности, рекомендуют назначать S_H = 1,1 при нормализации, термоулучшении или объемной закалке зубьев (при однородной структуре материала по всему объему); S_H = 1,2 при поверхностной закалке, цементации, азотировании (при неоднородной структуре материала по объему зуба);

Z_N ( K_HL ) − коэффициент долговечности,

, но 2,6 при S_H = 1,1;

и при S_H = 1,2.

Если , то следует принимать

Коэффициент Z_N учитывает возможность повышения допускаемых напряжений для кратковременно работающих передач ( при N_H < N_HG ).

Расчет числа циклов перемены напряжений выполняют с учетом режима нагружения передачи. Различают режимы постоянной и переменной нагрузки. При постоянном режиме нагрузки расчетное число циклов напряжений

где c − число зацеплений зуба за один оборот (для проектируемого одноступенчатого редуктора с = 1);

− частота вращения того зубчатого колеса, по материалу которого определяют допускаемые напряжения, об/мин;

t – время работы передачи (ресурс) в часах; t = L_h.

Таблица 2.2

Термообработка	Твердость зубьев^**		Группа сталей	^**, Па	SH	^**, МПа	SF	^**, МПа	^**, МПа
	на поверхности	в сердцевине
Нормализация, улучшение	180…350 НВ		40, 45, 40Х, 40ХН, 45ХЦ, 35ХМ и др.	2HB+70	1,1	1,8HB	1,75		2,74HB
Объемная закалка	45…55 HRC		40Х, 40ХН, 45ХЦ, 36 ХМ и др.	18HRC +150		550			1400
Закалка ТВЧ по всему контуру (модуль мм)	56…63 HRC 45…55 HRC	25…55 HRC	55ПП, У6, 35ХМ, 40Х, 40ХН и др.	17HRCпов +200	1,2	900 650		40HRCпов	1260
Закалка ТВЧ по всему контуру (модуль мм)	45…55 HRC		35ХМ, 40Х, 40ХН и др.	17HRCпов +200		550		40HRCпов	1430
Азотирование	55…67 HRC 50…59 HRC	24…40 HRC	35ХЮМ, 38ХМЮА 40Х, 40ХФА 40ХНМА и др	1050 1050	1,2	12HRCсердц +300	1,75	40HRCпов 30HRCпов	1000
Цементация и закалка	55…63 HRC	30…45 HRC	Цементируемые стали	23HRCпов		750		40HRCпов	1200
Нитроцементация и закалка	55…63 HRC	30…45 HRC	Молибденовые стали 25ХГМ, 25ХГНМ Безмолибденовые стали 25ХГТ, 35Х	23HRCпов		1000 750	1,5	40HRCпов	1520
* Распространяется на все сечения зуба и часть тела зубчатого колеса под основанием впадины. ** Приведён диапазон значений твёрдости, в котором справедливы рекомендуемые зависимости для пределов выносливости и предельных допускаемых напряжений (рассчитывают по средним значениям твёрдости в пределах допускаемого отклонения, указанного в таблице); HRCпов − твёрдость поверхности, HRCсердц − твёрдость сердцевины.

Постоянный режим нагрузки является наиболее тяжелым для передачи, поэтому его принимают за расчетный также в случае неопределенного (незадаваемого) режима нагружения.

Большинство режимов нагружения современных машин сводятся приближенно к шести типовым режимам (рис. 2.2):

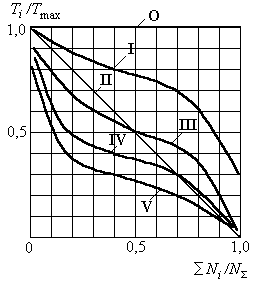
Рис. 2.2. 0 − постоянный, I − тяжелый, II − средний равновероятный, III − средний нормальный, IV − легкий, V − особо легкий

Режим работы передачи с переменной нагрузкой при расчете допускаемых контактных напряжений заменяют некоторым постоянным режимом, эквивалентным по усталостному воздействию. При этом в формулах расчетное число циклов N_H перемены напряжений заменяют эквивалентным числом циклов N_HE до разрушения при расчетном контактном напряжении.

где − коэффициент эквивалентности, значения которого для типовых режимов нагружения приведены в табл. 2.3.

Таблица 2.3

Режим работы	Расчёт на контакт. усталость			Расчёт на изгибную усталость
	Термооб- работка	m/2		Термическая обработка	m		Термическ. обработка	m
0	любая	3	1,0	улучшение, нормализация, азотирование	6	1,0	закалка объёмная, поверхност- ная, цементация	9	1,0
I			0,5			0,3			0,20
II			0,25			0,143			0,10
III			0,18			0,065			0,036
IV			0,125			0,038			0,016
V			0,063			0,013			0,004

Базовое число циклов N_HG перемены напряжений, соответствующее пределу контактной выносливости , рассчитывают по эмпирическим следующим зависимостям

Из двух значений (для зубьев шестерни и колеса) рассчитанного допускаемого контактного напряжения в дальнейшем за расчетное принимают:

– для прямозубых (цилиндрических и конических) передач – меньшее из двух значений допускаемых напряжений и ;

– для косозубых цилиндрических передач с твердостью рабочих поверхностей зубьев Н₁ и – меньшее из двух напряжений и

– для косозубых цилиндрических передач, у которых зубья шестерни значительно (не менее 70...80 НВ) тверже зубьев колеса,

где – меньшее из значений и .

Допускаемые напряжения изгиба

Расчет зубьев на изгибную выносливость выполняют отдельно для зубьев шестерни и колеса, для которых вычисляют допускаемые напряжения изгиба по формуле

где − предел выносливости зубьев по напряжениям изгиба, значения которого приведены в табл. 2.2;

S_F − коэффициент безопасности, рекомендуют S_F = 1,5...1,75 (смотри табл. 2.2);

Y_A(К_FC) − коэффициент, учитывающий влияние двустороннего приложения нагрузки (например, реверсивные передачи), при односторонней нагрузке Y_A = 1 и при реверсивной Y_A = 0,7...0,8 (здесь большие значения назначают при Н₁ и Н₂ > 350 НВ);

Y_N(K_FL) − коэффициент долговечности, методика расчета которого аналогична расчету Z_N (смотри выше).

При но

При Н > 350 НВ но

При следует принимать . Рекомендуют принимать для всех сталей . При постоянном режиме нагружения передачи

При переменных режимах нагрузки, подчиняющихся типовым режимам нагружения (рис. 2.2),

где принимают по табл. 2.3.

2.4. Проектный расчёт закрытой цилиндрической зубчатой передачи

При проектном расчёте прежде всего определяют главный параметр цилиндрической передачи межосевое расстояние , в мм. Расчёт производят по следующим формулам:

− для прямозубой передачи

− для косозубой передачи

В указанных формулах знак "+" принимают в расчётах передачи внешнего зацепления, а знак "–" – внутреннего зацепления.

Рекомендуется следующий порядок расчётов.

При необходимости определяют (или уточняют) величину вращающего момента на колесе передачи T₂ в Нмм. В случае задания в исходных данных на курсовой проект вращающего момента номинальный момент на колесе рассчитываемой передачи . При задании полезной мощности привода (кВт) номинальный вращающий момент на колесе рассчитывают по формуле , где – частота вращения вала колеса, мин ^-1.

Из табл. 2.4 назначают относительную ширину колёс в соответствии со схемой расположения колес относительно опор и выбранной ранее твёрдостью поверхностей зубьев. Бóльшие значения целесообразно принимать для передач с постоянными или близкими к ним нагрузками. В дальнейшем в расчетах может встретиться относительная ширина колес , которую рассчитывают с учетом зависимости

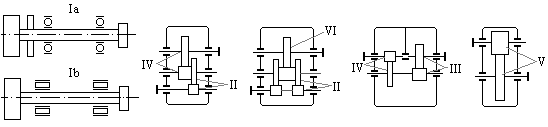
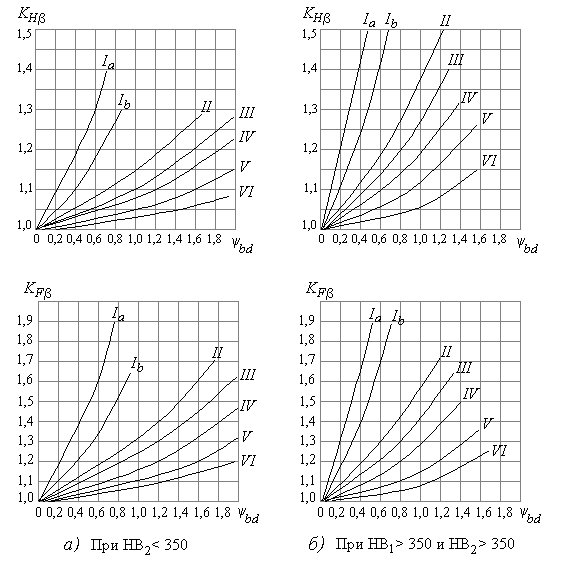
Рис. 2.3

Коэффициент неравномерности нагрузки по длине контакта выбирают по кривым на графиках рис. 2.3 а, б в соответствии с расположением зубчатых колёс передачи относительно опор, твёрдостью рабочих поверхностей зубьев и относительной шириной колес.

Приведённый модуль упругости E_пр в случае различных материалов колёс рассчитывают по соотношению

Если в передаче используется для изготовления колёс один материал (например, сталь с МПа или чугун с МПа), тогда E_пр =E , МПа.

Таблица 2.4. Относительная ширина колёс

Схема расположения колёс относительно опор	Твёрдость рабочих поверхностей зубьев
	или H1 и	H1 и H2 > 350 HB
Симметричная	0,3...0,5	0,25...0,3
Несимметричная	0,25...0,4	0,20...0,25
Консольная	0,20...0,25	0,15...0,20

Полученное значение межосевого расстояния (мм) для нестандартных передач рекомендуется округлить до ближайшего большего значения по одному из рядов нормальных линейных размеров (табл. 2.5).

Таблица 2.5. Нормальные линейные размеры, мм (ГОСТ 6636-69)

Ряды			Дополн. размеры	Ряды			Дополн. размеры
Ra10	Ra20	Ra40		Ra10	Ra20	Ra40
40	40	40		200	200	200
			41				205
		42				210
			44
	45	45			220	220
			46				230
		48				240
			49
50	50	50		250	250	250
			52
		53				260
			55				270
	56	56			280	280
			58				290
		60				300
			62				310
63	63	63		320	320	320
			65				330
		67				340
			70				350
	71	71			360	360
			73				370
		75				380
			78
80	80	80		400	400	400
			82				410
		85				420
							440
	90	90			450	450
			92				460
		95				480
			98				490
100	100	100		500	500	500
			102				515
		105				530
			108				545
	110	110	112		560	560
			115				580
		120				600
			118				615
125	125	125		630	630	630
		130				670	650
			135				690
	140	140			710	710
			145				730
		150				750
			155				775
160	160	160		800	800	800
			165				825
		170				850
			175				875
	180	180			900	900
			185				925
		190				950
			195				975

2.5. Геометрический расчёт закрытой цилиндрической передачи

Определяют модуль зацепления m (или m_n для косозубой передачи) из соотношения m(m_n) = (0,01...0,02)а_w , если H₁ и и m(m_n) = (0,016...0,0315)а_w , если H₁ и H₂ > 350 HB .

Полученное значение модуля необходимо округлить до стандартного значения по 1-му ряду модулей: 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10 мм. При этом для силовых передач рекомендуют принимать мм.

Для косозубой передачи угол наклона линии зуба назначают в пределах

Далее определяют суммарное число зубьев шестерни и колеса:

для прямозубых колёс

для косозубых колёс

Полученное значение округляют до целого числа.

Число зубьев шестерни определяют из соотношения: , где u – передаточное число передачи, Здесь знак "+" − для внешнего зацепления, знак "−" − для внутреннего зацепления.

Значение z₁ следует округлить до целого числа. Из условия отсутствия подрезания зубьев необходимо назначать: для прямозубых и − для косозубых колёс. Зачастую для уменьшения шума в быстроходных передачах принимают .

Рассчитывают число зубьев колеса передачи

Определяют фактическое значение передаточного числа передачи с точностью до двух знаков после запятой. Определяют или назначают фактическое межосевое расстояние a_wф цилиндрической зубчатой передачи. Для прямозубой передачи должно выполняться условие . Для косозубой передачи уточняют значение фактического угла наклона линии зуба

Рабочую ширину зубчатого венца колеса рассчитывают как и округляют до целого числа по ряду R_a20 нормальных линейных размеров (табл. 2.5). Тогда ширина зубчатого венца колеса , ширина зуба шестерни b₁ = b₂ + (2...5) мм.

Делительные диаметры рассчитывают по формулам:

– для прямозубых колёс

и − для косозубых колёс.

Начальный диаметр шестерни −

Начальный диаметр колеса передачи −

Диаметры вершин зубьев колёс для прямозубых и − для косозубых колёс. Диаметры впадин зубьев колёс − для прямозубых и − для косозубых колёс. Точность вычислений диаметральных размеров колёс должна быть не выше 0,001 мм. Угол зацепления передачи принимают равным углу профиля исходного контура:

2.6. Проверочный расчёт закрытой цилиндрической передачи

Проверка контактной выносливости рабочих поверхностей зубьев колёс

Расчётом должна быть проверена справедливость соблюдения следующих неравенств:

− для прямозубых колёс

− для косозубых колёс

где − коэффициент повышения прочности косозубых передач по контактным напряжениям,

Все геометрические параметры рассчитываемых колёс определены в п. 2.5. Для косозубой передачи дополнительно рассчитывают − коэффициент торцового перекрытия зубчатой передачи по формуле:

Здесь также знак "+" относится к передачам внешнего зацепления, а "–" – внутреннего зацепления.

Рассчитывают (или уточняют) величину вращающего момента Т₁ в Нмм на шестерне проверяемой передачи:

где − КПД передачи, он учитывает потери мощности в зубчатой передаче; обычно .

Для определения коэффициента внутренней динамической нагрузки K_HV необходимо по табл. 2.6 назначить степень точности передачи в зависимости от окружной скорости в зацеплении

м/с.

Таблица 2.6. Степени точности зубчатых передач

Степень точности	Окружные скорости вращения колёс V, м/с
	прямозубых		косозубых
	цилиндрических	конических	цилиндрических
6	до 15	до 12	до 30
7	до 10	до 8	до 15
8	до 6	до 4	до 10
9	до 2	до 1,5	до 4

Затем по табл. 2.7 находят значение коэффициента K_HV для рассчитываемой передачи.

В косозубой передаче теоретически зацепляется одновременно не менее двух пар зубьев. На практике ошибки нарезания зубьев могут устранить двухпарное зацепление, и при контакте одной пары между зубьями второй пары может быть небольшой зазор, который устраняется под нагрузкой вследствие упругих деформаций зубьев. Однако, первая пара зубьев нагружена больше, чем вторая на размер усилия, необходимого для устранения зазора. Это учитывают коэффициентом ,_, назначаемым из табл. 2.8.

Таблица 2.7. Значения коэффициентов K_HV и K_FV

Степень точности	Твёрдость поверхнос- тей зубьев	Коэф- фици- енты	Окружная скорость V, м/с
			1	3	5	8	10
6	а	KHV	1,03	1,09	1,16	1,25	1,32
			1,01	1,03	1,06	1,09	1,13
		KFV	1,06	1,18	1,32	1,50	1,64
			1,03	1,09	1,13	1,20	1,26
	б	KHV	1,02	1,06	1,10	1,16	1,20
			1,01	1,03	1,04	1,06	1,08
		KFV	1,02	1,06	1,10	1,16	1,20
			1,01	1,03	1,04	1,06	1,08
7	а	KHV	1,04	1,12	1,20	1,32	1,40
			1,02	1,06	1,08	1,13	1,16
		KFV	1,08	1,24	1,40	1,64	1,80
			1,03	1,09	1,16	1,25	1,32
	б	KHV	1,02	1,06	1,12	1,19	1,25
			1,01	1,03	1,05	1,08	1,10
		KFV	1,02	1,06	1,12	1,19	1,25
			1,01	1,03	1,05	1,08	1,10
8	а	KHV	1,05	1,15	1,24	1,38	1,48
			1,02	1,06	1,10	1,15	1,19
		KFV	1,10	1,30	1,48	1,77	1,96
			1,04	1,12	1,19	1,30	1,38
	б	KHV	1,03	1,09	1,15	1,24	1,30
			1,01	1,03	1,06	1,09	1,12
		KFV	1,03	1,09	1,15	1,24	1,30
			1,01	1,03	1,06	1,09	1,12
9	а	KHV	1,06	1,12	1,28	1,45	1,56
			1,02	1,06	1,11	1,18	1,22
		KFV	1,11	1,33	1,56	1,90	2,25
			1,04	1,12	1,22	1,36	1,45
	б	KHV	1,03	1,09	1,17	1,28	1,35
			1,01	1,03	1,07	1,11	1,14
		KFV	1,03	1,09	1,17	1,28	1,35
			1,01	1,03	1,07	1,11	1,14

Примечания к табл.2.7:

1. Твёрдость поверхностей зубьев

2. Верхние цифры относятся к прямым зубьям, нижние – к косым зубьям.

Таблица 2.8

Окружная скорость V , м/с	Степень точности
До 5	7	1,03	1,07
	8	1,07	1,22
	9	1,13	1,35
5…10	7	1,05	1,20
	8	1,10	1,30
10…15	7	1,08	1,25
	8	1,15	1,40

Если в результате проверки выявится существенная недогрузка (свыше 10%) передачи, то с целью более полного использования возможностей материалов зубчатых колёс возможна корректировка рабочей ширины зубчатого венца по соотношению

Уточнённое значение рабочей ширины венца рекомендуется округлить до нормального линейного размера (по табл. 2.5).

Проверка прочности зубьев по напряжениям изгиба

Расчёт выполняют отдельно для шестерни и для зубчатого колеса передачи после уточнения нагрузок на зубчатые колёса и их геометрических параметров.

Проверяют справедливость соотношения расчётных напряжений изгиба и допускаемых напряжений []:

− для прямозубых колёс

− для косозубых колёс

где − коэффициент повышения прочности косозубых передач по напряжениям изгиба, Здесь − коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии на зубе к основанию зуба, , где подставляют в градусах. Коэффициент неравномерности распределения нагрузки между одновременно зацепляющимися зубьями назначают по табл. 2.8.

Окружное усилие в зацеплении колёс рассчитывают по формуле

Н.

Коэффициент неравномерности распределения нагрузки по длине линии контакта определяют по графикам рис. 2.3 а, б, аналогично рассмотренному выше определению значения коэффициента .

Коэффициент формы зуба Y_F для прямозубых колёс назначают по табл. 2.9 в зависимости от фактического числа зубьев для прямозубых колёс и от числа зубьев эквивалентных колёс − для косозубых колес. Табл. 2.9 составлена для случая отсутствия смещения зуборезного инструмента (x = 0) при зубонарезании.

Если при проверочном расчёте рабочие напряжения изгиба в зубьях колёс оказываются значительно меньшей величины, чем допускаемые напряжения , то для закрытых передач это вполне допустимо, так как нагрузочная способность таких передач ограничивается, как правило, контактной выносливостью зубьев.

Таблица 2.9. Коэффициент формы зуба Y_F

Z или ZV	YF	Z или ZV	YF	Z или ZV	YF	Z или ZV	YF	Z или ZV	YF
16	4,29	25	4,00	35	3,85	60	3,69	100	3,60
17	4,25	26	3,98	40	3,80	65	3,67	120	3,58
20	4,13	28	3,94	45	3,76	70	3,66	150	3,56
22	4,07	30	3,91	50	3,73	80	3,64	180	3,54
24	4,02	32	3,88	55	3,71	90	3,62		3,47

2.7. Расчёт открытой цилиндрической зубчатой передачи

Учитывая условия и характер работы открытых передач (недостаточная защищённость от загрязнения абразивными частицами и увеличенный абразивный износ при плохой смазке, большие деформации валов, что приводит к увеличению зазоров в зацеплении, возрастанию динамических нагрузок, к понижению прочности изношенных зубьев вследствие уменьшения площади их поперечного сечения и, как следствие, к поломке зубьев), данные передачи рекомендуют рассчитывать по напряжениям изгиба. В этих передачах выкрашивание не наблюдается, так как поверхностные слои зубьев изнашиваются и удаляются раньше, чем появляются усталостные трещины.

Для проектного расчёта открытых передач по напряжениям изгиба определяют модуль зацепления из выражений:

− для прямозубых колес

− для косозубых колес

Здесь: z₃ − число зубьев шестерни открытой передачи (см. исходные данные);

− коэффициент ширины зубчатого венца колеса относительно начального диаметра шестерни, рекомендуют назначать для открытых передач

− допускаемое напряжение изгиба зубьев шестерни, Н/мм², определяют в соответствии с п. 2.3. («Расчет допускаемых напряжений»);

Т₃ − момент на шестерне, Нм;

− смотри выше, для проектного расчета принять 8;

− смотри рис. 2.3;

Y_F3 − смотри табл. 2.9.

Полученное значение модуля округляют в большую сторону до значения из стандартного ряда модулей (см. п. 2.5).

Зная значение модуля, определяют геометрические размеры шестерни :

диаметр делительный − или

диаметр вершин зубьев −

диаметр впадин зубьев −

ширина венца −

Точность вычисления диаметров шестерни до 0,001 мм, значение ширины зубчатого венца округляют до целого числа по нормальным линейным размерам (см. табл. 2.5). Проверочный расчет такой передачи по контактным напряжениям выполняют в соответствии с п. 2.6. («Проверочный расчет закрытой цилиндрической передачи»).

2.8. Расчёт закрытой конической зубчатой передачи

Наибольшее применение в редукторостроении получили прямозубые конические колёса, у которых оси валов пересекаются под углом (рис. 2.4), так называемые ортогональные передачи.

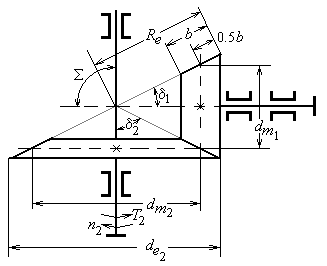
Рис. 2.4

Проектный расчёт

Основной габаритный размер передачи − делительный диаметр колеса по внешнему торцу − рассчитывают по формуле:

где Е_пр − приведённый модуль упругости, для стальных колёс МПа;

T₂ − вращающий момент на валу колеса, Нмм (см.п.2.4);

− коэффициент неравномерности распределения нагрузки по длине зуба, определяют по графикам на рис. 2.5.

Здесь К_be − коэффициент ширины зубчатого венца относительно внешнего конусного расстояния, К_be = b_w / R_e. Рекомендуют принять . Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H₁ и H₂ > 350 HB или V > 15 м/с .

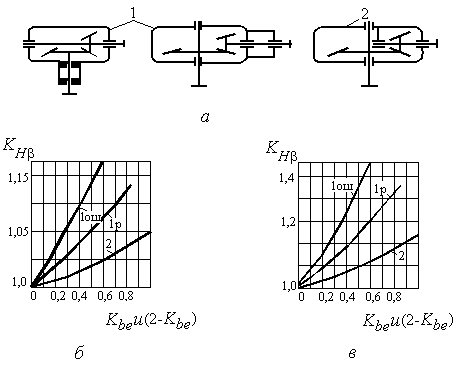
Рис. 2.5

Наиболее распространено в редукторостроении значение К_be = 0,285, тогда предыдущее выражение для определения делительного диаметра по внешнему торцу колеса принимает вид

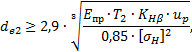
где – расчетное передаточное число конической передачи, или u_p = z₂ / z₁.

Геометрический расчёт

Определяют делительный диаметр шестерни по внешнему торцу

Число зубьев шестерни назначают по рекомендациям, представленным на рис. 2.6.

По значению определяют число зубьев шестерни:

при Н₁ и

при и

при Н₁ и

Вычисленное значение z₁ округляют до целого числа.

Рис. 2.6

Определяют число зубьев колеса

Вычисленное значение округляют до целого числа. После этого необходимо уточнить:

- передаточное число передачи

- угол делительного конуса колеса

- угол делительного конуса шестерни

- внешний окружной модуль

Рекомендуется округлить m_e до стандартного значения m_eф по ряду модулей: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10. После этого уточняют величины диаметров и

Рассчитывают величину внешнего конусного расстояния передачи (рис. 2.4)

Рабочая ширина зубчатого венца колеса определяют как

Полученное значение округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5).

Определяют расчётный модуль зацепления в среднем сечении зуба

При этом найденное значение не округляют!

Рассчитывают внешнюю высоту головки зуба

Внешнюю высоту ножки зуба определяют как

Внешний диаметр вершин зубьев колёс рассчитывают по формуле

Угол ножки зуба рассчитывают по формуле

Проверочный расчёт

При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия

где E_пр − приведённый модуль упругости, для стальных колёс МПа;

− вращающий момент на шестерне, Нмм,

здесь − КПД передачи.

− коэффициент расчётной нагрузки, ; коэффициент концентрации нагрузки найден ранее по графикам рис. 2.5.

− коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости в соответствии с рекомендациями (табл. 2.6);

− делительный диаметр шестерни в среднем сечении зуба,

− угол зацепления,

Далее проверяют зубья колёс на выносливость по напряжениям изгиба по формулам:

и

где − окружное усилие в зацеплении, Н,

− коэффициент расчётной нагрузки, Здесь , а определяют по табл. 2.7 с понижением точности на одну степень против фактической.

− коэффициент формы зуба соответственно шестерни и колеса, находят по табл. 2.9 в зависимости от эквивалентного числа зубьев колёс

2.9. Проектный расчёт открытой конической прямозубой передачи

Модуль зацепления в среднем сечении зуба конического колеса рассчитывают по формуле

где, кроме рассмотренных выше величин (см. п. 2.7), рекомендуют назначить и

Далее рассчитывают основные геометрические параметры зубчатых колёс открытой передачи:

− ширину зубчатого венца (с округлением до целого числа по ряду нормальных линейных размеров);

− делительный диаметр в среднем сечении зуба шестерни

− по заданному (или принятому) передаточному числу u_отк находим угол при вершине делительного конуса

− среднее конусное расстояние

− внешнее конусное расстояние

− модуль зацепления на внешнем торце

− внешний делительный диаметр шестерни

Проверочный расчет такой передачи на выносливость по контактным напряжениям выполняют в соответствии с п. 2.8 («Расчет закрытой конической зубчатой передачи»).

2.10. Конструирование зубчатых колес

2.10.1. Цилиндрические зубчатые колеса внешнего зацепления

Форма зубчатого колеса зависит от его габаритных размеров, от серийности производства. При отсутствии в техническом задании на курсовое проектирование указаний о серийности производства редукторов его можно задать, отдавая предпочтение индивидуальному и мелкосерийному производству. На рис. 2.7 приведены простейшие формы колес, изготовляемых в единичном и мелкосерийном производстве.

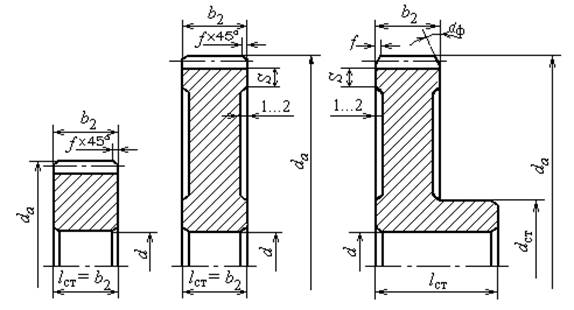
Рис. 2.7

При небольших диаметрах колес их изготавливают из прутка, а при больших заготовки колес получают свободной ковкой с последующей токарной обработкой. Чтобы уменьшить объем точной обработки резанием, на дисках колес выполняют выточки. При диаметрах d_a < 80 мм эти выточки, как правило, не делают.

Длину l_ст посадочного отверстия колеса желательно принимать равной или больше ширины b₂ зубчатого венца колеса. Длину ступицы l_ст согласуют также с расчетами соединения (шпоночного, шлицевого или с натягом), выбранного для передачи вращающего момента с колеса на вал (или с вала на колесо), и с диаметром посадочного отверстия d:

l_ст = (0,8...1,5)d, обычно l_ст = (1...1,2)d.

Выступающую часть ступицы располагают по направлению действия осевой силы в зацеплении. В одноступенчатых редукторах колеса делают со ступицей, симметрично выступающей в обе стороны от диска колеса.

Диаметр d_ст ступицы назначают в зависимости от материала колеса: для стали − d_ст = (1,5...1,55)d; для чугуна − d_ст = (1.55...1,6)d; для легких сплавов − d_ст = (1,6...1,7)d; меньшие значения принимают для шлицевого соединения вала с колесом, большие - для шпоночного и соединения с натягом.

Ширину S торцов зубчатого венца принимают S = 2,2m + 0,05b₂ , где m − модуль зацепления, мм.

На торцах зубчатого венца выполняют фаски: при твердости рабочих поверхностей зубьев менее 350 НВ − , при более высокой твердости - под углом на всю высоту зуба. Обычно f = (0,5...0,6)m.

При серийном производстве колес заготовки получают из прутка свободной ковкой (рис. 2.8), а при годовом объеме выпуска колес более 100 штук применяют двусторонние штампы (рис. 2.9).

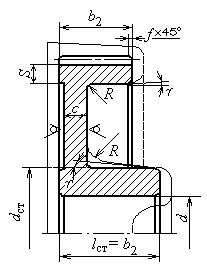
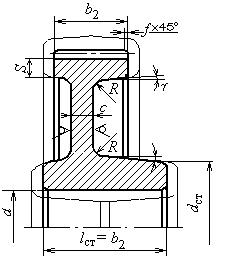
Рис.2.8 Рис.2.9

Для свободной выемки заготовок из штампа принимают значения штамповочных уклонов и радиусов закруглений мм.

Толщина диска С рекомендована для уменьшения влияния термической обработки на точность геометрической формы колеса

С = (0,35...0,4)b₂ .

2.10.2. Цилиндрические зубчатые колеса внутреннего зацепления

Размеры d_ст, l_ст, S, f основных конструктивных элементов колес внутреннего зацепления (рис. 2.10) принимают по соотношениям для колес внешнего зацепления.

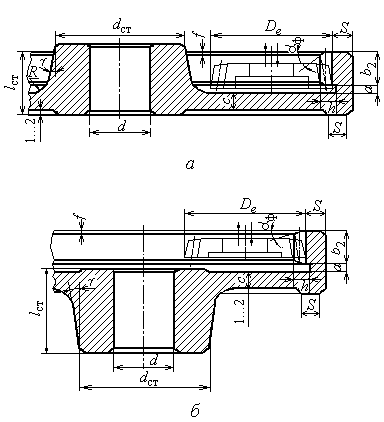
Рис. 2.10

Конструктивное исполнение колес внутреннего зацепления может быть выполнено по одному из вариантов, показанных на рис. 2.10, а, б и отличающихся расположением ступицы относительно зубчатого венца: а − ступица расположена внутри колеса, что обеспечивает лучшие условия работы зацепления по сравнению с вариантом б, в котором ступица вынесена за контур зубчатого венца. Однако вариант а можно применять в том случае, если между ступицей колеса и внутренней поверхностью зубчатого венца размещается зуборезный долбяк, которым изготовляют зубья колеса.

В табл. 2.10 приведены рекомендуемые диаметры D_e долбяка и размер ширины канавки а для выхода долбяка и размещения стружки, образующейся при долблении зубьев прямозубых колес.

Таблица 2.10

m, мм	1,5	2,0	2,5	3,0	3,5	4,0	5,0	6,0	8,0
De, мм	54	56	55	60	56	112	110	120	128
a, мм	5		6			7		8	9

Размер а канавки в косозубых колесах внутреннего зацепления увеличивают на 30...40. Глубину канавки во всех случаях принимают h = 2,5m, толщину диска колеса С = (0,3...0,35)b₂.

2.10.3. Конические зубчатые колеса

Конструктивные формы конических зубчатых колес с внешним диаметром вершин зубьев мм представлены на рис. 2.11.

При угле делительного конуса колеса допускаются обе конструкции конических колес. Размер ступицы колеса определяют по рекомендациям для цилиндрических зубчатых колес.

При внешнем диаметре вершин зубьев колеса свыше 120 мм рекомендуют конструкции колес, показанные на рис. 3.6.

По форме на рис. 3.6, а конструируют колеса при единичном или мелкосерийном производстве. Колеса меньших диаметров изготавливают точением из прутка (из цилиндрической заготовки), больших − свободной ковкой с последующей токарной обработкой.

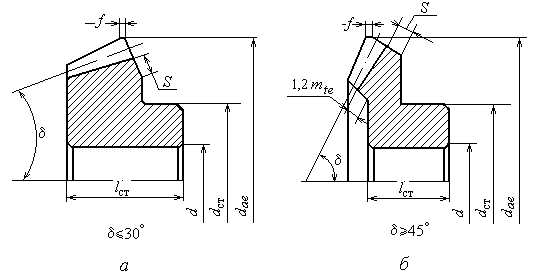
Рис. 2.11

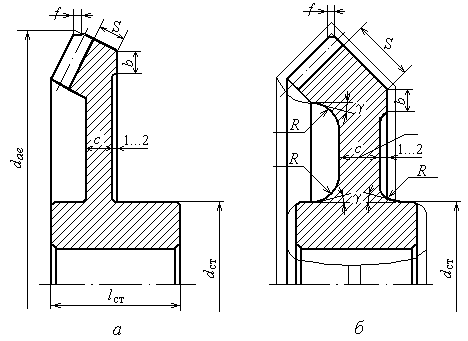
Рис.2.12

По рис. 2.12, б конструируют конические колеса при крупносерийном производстве. Тонкими линиями показаны контуры заготовки колеса, получаемой ковкой в двусторонних штампах (штамповкой).

При любой форме колес внешние углы зубьев притупляют фаской . Ширину зубчатого венца принимают равной S=2,5m_е+2 мм. Торец зубчатого венца шириной b = 0,7S используют для установки заготовки колеса в приспособлении при нарезании зубьев на станке. Для уменьшения объема точной механической обработки выполняют выточки глубиной 1...2 мм.

2.10.4. Валы - шестерни

Принципиально возможны два конструктивных исполнения шестерен зубчатых передач: за одно целое с валом (вал - шестерня) и отдельно от вала (насадная шестерня). Качество вала - шестерни (жесткость, точность зацепления и т.п.) оказывается выше, а стоимость изготовления ниже, чем вала с насадной шестерней, поэтому все шестерни редукторов, как правило, выполняют за одно целое с валом. На рис. 2.13 показаны характерные конструктивные формы вала - шестерни.

На рис. 2.13, а конструкция шестерни обеспечивает нарезание зубьев со свободным выходом зуборезного инструмента (червячной фрезы или долбяка). При больших передаточных числах передачи наружный диаметр шестерни, как правило, мало отличается от диаметра вала, и валы - шестерни конструируют в этом случае по форме на рис. 2.13, б.

Выход червячной фрезы определяют графически по ее наружному диаметру D_ф, назначаемому в зависимости от модуля зацепления и степени точности передачи по следующим рекомендациям:

m, мм		2…2,25	2,5…2,75	3…3,75	4…4,5	5…5,5	6…7
Dф, мм	7 степень точности	90	100	112	125	140	160
	8...10 степень точн.	70	80	90	100	112	125

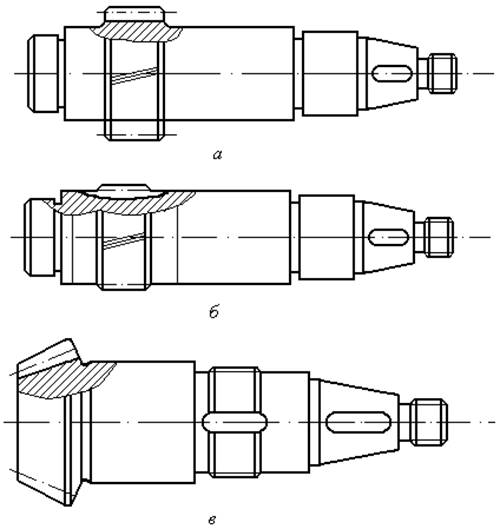
Рис. 2.13

По возможности желательно избегать конструкции врезных шестерен, так как в этом случае затрудняется работа червячной фрезы или шлифовального круга (при чистовой обработке зубьев).

На рис.2.13, в показан вариант конструкции конического вала - шестерни.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00