Главная
Лекция 15 (продолжение). Примеры решения на динамические нагрузки
Расчеты при ударных нагрузках
Пример 1.
Груз
весом Р = 2 кН, скользя без трения вдоль стального бруса, падает на
приваренную к нему жесткую пластину и вызывает ударное растяжение бруса.
Площадь поперечного сечения бруса А =
0,0005 м2 (рис. а), его длина
l = 1,8 м, модуль продольной
упругости материала бруса Е =2·105 МПа;
высота падения груза Н равна 0,02 м.
Требуется
определить максимальное нормальное напряжение в брусе в момент его наибольшей
деформации. Собственной массой стального бруса, испытывающего удар, пренебречь.
Решение.
Определим
величину 
(рис. б)
Рассчитываем
динамический коэффициент, используя формулу 
Определяем статическое нормальное напряжение
Находим максимальное динамическое напряжение
.
Пример 2.
Груз весом Р = 200 Н падает с высоты Н = 0,3 м посередине на шарнирно опертую двухопорную деревянную балку квадратного поперечного сечения со стороной а = 15 см и длиной l = 3 м. Рассчитать запас прочности балки, если модуль продольной упругости материала балки Е = 104 МПа, а предел прочности при расчете на изгиб RИ = 20 МПа. Собственной массой балки, испытывающей удар, пренебречь.
Решение.
Проводим статический расчет, т.е. определяем максимальное напряжение и перемещение в серединном сечении балки при нагружении ее статической сосредоточенной силой Р = 200 Н.
Максимальный изгибающий момент равен
Статический момент площади сечения равен
Определяем максимальное нормальное статическое напряжение
Статическое перемещение посередине балки определяем по известной из теории изгиба формуле
Рассчитываем динамический коэффициент
Находим динамическое напряжение
МПа.
Запас прочности равен
Пример 3.
Для заданной упругой системы определить:
- максимальные
напряжения, возникающие при ударе об нее груза 
, падающего с высоты 
;
- величину перемещения в направлении удара в том сечении, в котором прикладывается ударная нагрузка в направлении удара.
Материал
упругой системы: Сталь (
). Массой упругой системы пренебречь. Рычаг в заданиях
на скручивающий удар считать абсолютно жестким.
Решение.
Рассмотрим различные примеры ударного нагружения.
Осевое
действие ударной нагрузки.
Пусть на
ступенчатый стержень квадратного поперечного сечения с высоты падает груз .
Стороны
квадратного сечения: 
; 
.
Длины участков
Динамические напряжения в стальном стержне определяются по формуле
,
где 
- напряжение,
возникающее в материале стержня при воздействии на стержень статически
приложенной нагрузки 
в месте удара.
- коэффициент
динамичности.
При
статическом приложении нагрузки в месте удара в любом
сечении стержня будет возникать продольная сила
.
При этом
максимальное напряжение будет в сечениях с меньшей площадью поперечного
сечения, т. е. в любом сечении участка с длиной 
, для которого сторона квадратного сечения равна 
.
Знак минус указывает на сжимающее нормальное напряжение.
Коэффициент
динамичности зависит от высоты
падения груза и статической
деформации 
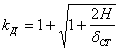
Статическая
деформация будет складываться из
деформаций участков
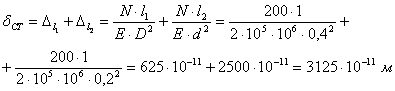
Максимальное динамическое напряжение
Динамическая деформация сечения, в котором прикладывается ударная нагрузка
Скручивающий
удар.
Пусть
стержень, длиной 
и диаметром , испытывает скручивающий удар от нагрузки , падающей с высоты на абсолютно жесткий
рычаг длиной 
. Определим максимальное напряжение и величину перемещения
сечения в месте приложения ударной нагрузки.
Предварительно определим статические значения напряжения и перемещения.
Пренебрегая
деформацией рычага и полагая, что вследствие малости перемещения проекция на
вертикаль перемещения точки соударения равна длине дуги с радиусом 
, можно вычислить по
формуле
,
где 
- модуль сдвига 
. Принимаем 
;
- полярный момент
инерции. Для круглого поперечного сечения
Коэффициент
динамичности
Максимальное
статическое напряжение при действии закручивающего момента 
.
- полярный момент
сопротивления. Для круглого поперечного сечения
Динамическое напряжение
Динамическое перемещение
Изгибающий
удар.
Пусть на
свободный конец консольной балки длиной прямоугольного
поперечного сечения с шириной сечения 
и высотой сечения 
падает груз с высоты .
Определим максимальное напряжение и величину перемещения сечения в месте приложения ударной нагрузки.
Статическое перемещение определим способом Верещагина
Коэффициент динамичности
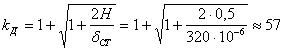
Максимальное статическое напряжение будет возникать в опорном сечении
Динамическое напряжение
Динамическое перемещение
Пример 4.
Стальной
стержень диаметром d = 
МПа?
Решение.
Динамическое
напряжение 
, где статическое напряжение
.
Вес
груза 
,
Статическое
напряжение 
.
Коэффициент
динамичности 
(без учета собственной
массы стержня), где статическая деформация
.
Коэффициент динамичности 
Для жесткого
стержня единицами в формуле 
можно было бы пренебречь.
Динамическое
напряжение 
.
Для дюралюминиевого стержня
,
.
Таким образом, замена материала позволяет снизить напряжения в 1,69 раза.
Пример 5.
Для данной схемы определить максимальные ударные напряжения и максимальный прогиб, если масса падающего груза m = 50 кг, высота падения h = 40 мм, сечение балки – двутавр № 14: WX = 81,7 см3, IX = = 572 см4, материал балки – сталь.
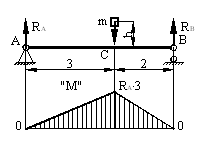
Решение.
Определяем опорные реакции
; 
; 
Проверка:
; 
-
верно
Определяем статический прогиб балки
Прогиб балки определим по методу начальных параметров.
Составляем
уравнение прогибов для точки С
Определяем начальные параметры
. Для нахождения 
составим уравнение
прогибов для точки В,
приравняв его к нулю, найдем искомую величину.
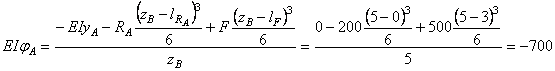
Находим прогиб в точке С
Определяем ударный коэффициент
Определяем напряжения в балке от статического действия нагрузки
Изгибающий момент будет иметь максимальное значение в точке С (см. рис.), а его величина определится по формуле:
Тогда напряжения в точке С:
Определяем динамический прогиб и напряжения
Пример 6.
Найти наибольшее нормальное напряжение в шарнирно опертой двутавровой
балке, возникающее при падении на нее груза весом 
кН с высоты 
см (см. рис.). Оценить
прочность балки при 
кН/см2. Номер двутавра – 20,
м, 
.
Решение.
Наибольшее нормальное напряжение 
, возникающее в балке при ударе, определяется по формуле
,
где 
– коэффициент
динамичности при ударе; 
– наибольшее
нормальное напряжение, которое возникло бы в балке при статическом приложении нагрузки,
равной G.
Коэффициент
динамичности при ударе вычисляется по формуле
,
где 
– статический прогиб балки в месте
падения груза весом G,
вызванный его статическим приложением.
1. Строим
эпюру изгибающих моментов 
от силы кН, приложенной к
балке статически.
Сначала
определяем опорную реакцию 
. Направим ее вверх и составим уравнение статики 
. Получим:
.
Отсюда
находим, что
.
Тогда изгибающий
момент под сосредоточенной силой равен:
кНм.
2. В месте
падения груза весом G
прикладываем к балке единичную силу 
и строим от нее
единичную эпюру изгибающих моментов 
.
В этом случае 
и тогда ордината
единичной эпюры моментов под силой равна
м.
3. Определяем статический прогиб балки 
в месте падения груза
весом G, перемножая полученные эпюры по
правилу трапеций:
.
Для двутавра № 20 осевой
момент инерции 
см4.
Модуль Юнга 
кН/см2. Тогда статический прогиб:
см.
4. Коэффициент
динамичности равен:
.
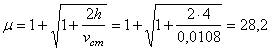5. Вычисляем
наибольшее статическое напряжение, возникающее в поперечном сечении балки (
кНм = 63 кНсм;
см3):
кН/см2.
6. Вычисляем
наибольшее динамическое напряжение в балке:
кН/см2.
Прочность балки
при ударе обеспечена, поскольку
кН/см2 < кН/см2.
Пример 7.
Груз G = 1,2 кН падает с
высоты h = 0,12 м в
точку С двутавровой балки КD, опирающейся на упругое сооружение,
состоящее из двух балок АК и DМ (рис. 1, а). Сечение балки КD -
двутавр №18 (
м4 ; 
м3).
Сечение балок АК и DМ - двутавр №30 (
м4; 
м3). Длина
балок l = 1,2 м.
Модуль упругости 
кН/м2.
Требуется:
Определить динамические напряжения в опасных сечениях балок. Сравнить полученные напряжения с теми, которые появятся в балках, если балка КD будет опираться на абсолютно жесткое основание.
Рис. 1
Решение.
Из уравнений
равновесия балки 
и 
находим опорные
реакции RK , RD :
кН;
кН.
Для проверки
правильности найденных опорных реакций составляем уравнение равновесия 
: 0,8 + 0,4 - 1,2 =
0; 0=0.
Затем строим эпюры изгибающих моментов и поперечных сил для рассматриваемой балки КD и двух консольных балок АК и DМ (рис. 1, б, в, г, д, е).
1. Определение полного статического прогиба сечения С балки КD.
Сначала определим статический прогиб сечения С балки КD при опирании ее на абсолютно жесткое основание. Составим уравнение прогиба методом начальных параметров, приняв начало координат в сечении К:
.
(1)
При этом, 
; 
; 
; 
. Для нахождения 
используем условие
отсутствия прогиба в сечении D: 
. При z = l м имеем:
; 
.
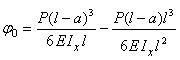Теперь,
подставив найденное значение в уравнение (1),
получим формулу для определения прогиба сечения С:
м.
Для определения полного прогиба сечения С с учетом упругого характера опирания балки КD (рис. 1, ж) необходимо предварительно найти прогибы концов консольных балок АК и DМ. Для этого воспользуемся формулой, полученной в примере 34:
м;
м.
Эпюра перемещений для составной конструкции из балок изображена на рис. 1, ж. Величину полного перемещения сечения С балки с учетом перемещения его в результате смещения опор балки КD, опирающейся на консольные балки, определяем по формуле:
.
2. Определение динамических коэффициентов и напряжений.
Динамический коэффициент при падении груза G на балку КD, опирающуюся на консольные балки АК и DМ, определяем по формуле:
а при опирании балки КD на абсолютно жесткое основание -
.
Для вычисления динамических напряжений необходимо вначале определить статические напряжения, возникающие в сечении С:
кН/м2,
а затем динамические напряжения:
.
Динамические напряжения, возникающие в сечении С балки КD, опирающейся на консольные балки,
кН/м2,
и динамические напряжения, возникающие в сечении С балки КD, опирающейся на абсолютно жесткое основание:
кН/м2.
Таким образом,
если опоры лежат на абсолютно жестком основание, то в сечении С возникают
динамические напряжения в 
раза большие по величине. Статические напряжения, возникающие
в сечении А:
кН/м2.
При динамическом коэффициенте КД = 78,1, полученном в предположении упругого опирания балки КD в точках К и D, находим динамические напряжения в сечении А:
кН/м2.
Статическое и динамическое напряжения в сечении М балки DМ:
кН/м2.
кН/м2.
Следовательно, вне зависимости от того, на какое основание опирается балка KD, опасное сечение находится в точке удара.
Пример 8.
На раму,
показанную на рис. 1, падает груз Q с высоты 
. Вес
груза 
,
поперечное сечение рамы – двутавр № 20. Требуется найти максимальные нормальные
напряжения в опасном сечении рамы и прогиб в точке удара от ударного действия
нагрузки.
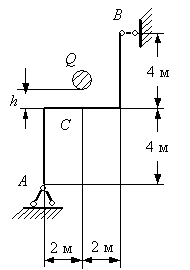
Рис.1
Решение.
Чтобы
определить динамический коэффициент по формуле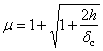 
, необходимо найти
прогиб 
точки С (точки
приложения нагрузки Q) от статического действия
нагрузки. Найдем этот прогиб, используя метод Максвелла–Мора и интегрируя
формулу Максвелла–Мора с помощью правила Верещагина. Для этого построим эпюры
изгибающих моментов от нагрузки Q (рис. 2, а) и от единичной силы, соответствующей
искомому перемещению (рис. 2, б).
Перемножим эти эпюры по правилу Верещагина:
.
Подставляя величину жесткости для двутавра № 20, сосчитаем прогиб в "см"
Рис.2
.
Найдем
динамический коэффициент по формуле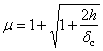
.
Определим
максимальные нормальные напряжения в опасном сечении от статического действия
нагрузки. В рассматриваемом примере несколько равно опасных сечений с
изгибающим моментом 
. Максимальные статические напряжения равны
.
Динамические
напряжения от действия ударной нагрузки увеличатся согласно формуле 
в раз.
.
Видно, что
динамические напряжения не превосходят предела пропорциональности 
= 200 МПа, и материал работает упруго.
Во столько же раз увеличится и динамический прогиб:
.
Пример 9.
Дано: на раму падает груз весом P с некоторой высоты h (рис.1)
материал –
сталь, 
= 160 МПа, 
МПа;
a = 0,6 м, b = 0,2 м, c = 0,8 м; d = 11 см, P = 1 кН, h = 14 см;
Требуется:
1) раскрыть статическую неопределимость рамы;
2) определить динамический коэффициент;
3) определить динамические напряжения и прогибы;
Рис.1
Решение:
Рис.2
Решение.
1. Раскрытие статической неопредимости рамы
Выбираем эквивалентную систему, отбрасывая реакцию катка и заменяя ее неизвестной силой X1 (рис. 2, а).
а) построение грузовой эпюры
Определяем реакцию заделки A, проецируя все внешние силы на ось y (рис. 2, б):
Изгибающий момент от статической силы P на 2 участке будет:
в сечении D момент равен 0, в сечении A:
Строим эпюру моментов от силы P (рис. 2, в).
б) построение эпюры моментов от единичной силы
Вместо
неизвестной X1 прикладываем единичную
силу 
и рассматриваем ее
действие на раму (рис. 2, г).
Реакция заделки в этом случае равна:
Изгибающий момент от единичной силы равен:
в сечении C момент равен 0, в сечении A:
Строим эпюру моментов от единичной силы (рис.2, д).
в) решение канонического уравнения
В сечении B приложения неизвестной реакции прогиб равен 0 (т.к. катковая опора препятствует вертикальному перемещению), поэтому и в сечении C прогиб равен 0, т.е. суммарный прогиб от действия неизвестной реакции X1 и силы P равен 0:
где 
, 
– прогибы от действия
единичной силы и силы P.
Находим прогибы способом Верещагина:
где 
– площадь фигуры на грузовой эпюре, 
– ордината под центром
тяжести этой фигуры на эпюре единичной силы.
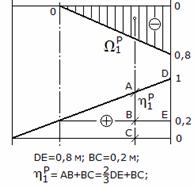
Рис.3
Находим прогиб от единичной силы: площадью фигуры в формуле Верещагина будет площадь эпюры единичной силы, ординатой – ордината под центром тяжести эпюры единичной силы (2/3 высоты эпюры); поэтому:
Находим прогиб от силы P: площадью фигуры будет площадь грузовой эпюры, ординатой – ордината на эпюре единичной силы под центром тяжести грузовой эпюры (рис. 3); поэтому:
Тогда, решая каноническое уравнение получаем:
Неизвестная
реакция X1 равна по величине 
и направлена по направлению единичной силы.
2. Определение статического прогиба и динамического коэффициента
а) построение эпюры изгибающих моментов
Определяем реакцию заделки A с учетом реакции отброшенной опоры (рис. 2, е):
Изгибающий момент на 1 участке равен:
в сечении C момент равен 0, в сечении D:
Изгибающий момент на 2 участке:
в сечении А момент равен:
Строим эпюру изгибающих моментов (рис. 2, ж).
б) построение эпюры единичной силы
В сечении D прикладываем единичную силу и рассматриваем ее действие на раму (рис. 2, з). Момент от единичной силы возникает только на 2 участке рамы:
в сечении D момент равен 0, в сечении A:
Строим эпюру изгибающего момента от единичной силы (рис. 2, и).
в) определение статического прогиба
Определяем статический прогиб с помощью интеграла Мора:
где Mи(P), Mи(1) – изгибающие моменты, возникающие под действием силы P и единичной силы.
В данном случае:
но т.к. на 1 участке единичная сила момента не создает, то первое слагаемое обращается в ноль:
с учетом моментов, создаваемых силой P и единичной силой на 2 участке получаем:
Учитывая, что сечение рамы круглое, находим его момент инерции:
тогда статический прогиб равен:
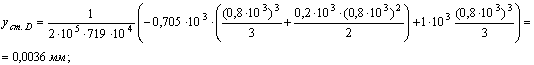
Вычисляем динамический коэффициент по приближенной формуле:
3. Определение динамических напряжений и прогибов
Динамические напряжения определяются как:
Учитывая, что сечение рамы круглое, находим его момент сопротивления:
Считая статический изгибающий момент максимальным, действующим в сечениях рамы, находим максимальные динамические напряжения:
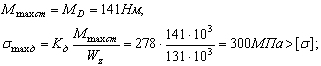
Таким образом,
максимальные динамические напряжения превышают допустимые напряжения
подбираем новое сечение рамы, исходя из условия прочности:
Округляем диаметр нового сечения рамы до стандартного 
выбранного из ряда Ra 40 нормальных линейных размеров (ГОСТ 6636–69),
тогда для нового сечения:
Максимальные динамические напряжения, возникающие в раме с новым сечением:
Определяем статический прогиб для рамы с новым сечением:
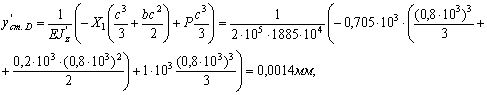
Пересчитываем динамический коэффициент:
Динамический прогиб в сечении падения груза будет:
Онлайн-калькулятор "Расчет коэффициента динамичности при падении груза на конструкцию"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов
