Главная
Лекция 15 (продолжение). Примеры решения на динамические нагрузки
Расчеты на усталостную прочность
Пример 1.
Круглый вал
диаметром 
= 80 МПа, 
=55 МПа, 
=35 МПа; 
=28 МПа и 
=20 МПа.
Вал изгибается
моментом, меняющимся от 
до 
=600 Нм, и
скручивается моментом, меняющимся от нуля до 
= 1800 Нм; при этом наибольших и наименьших
своих значений изгибающий и крутящий моменты достигают одновременно.
Коэффициент динамичности нагрузки для переменной составляющей цикла нормальных
и касательных напряжений равен 2; коэффициент запаса прочности 1,8. Проверить
прочность вала.
Решение.
Условие прочности вала, подвергающегося одновременно изгибу и кручению, может быть написано так:
Здесь 
и 
- допускаемые напряжения при изгибе и кручении, определяемые
для детали в зависимости от степени асимметрии цикла нормальных и касательных
напряжений.
Определим и .
Характеристика
цикла при изгибе 
.
Величину допускаемого напряжения при изгибе (симметричный цикл) определим по формуле
Величину
теоретического коэффициента концентрации напряжений при изгибе вала с галтелью
находим по таблице. Для отношения 
, применяя линейную интерполяцию между значениями 
при 
и 
при 
,
имеем 
.
Величину коэффициента чувствительности определяем по графику; при и 
МПа имеем q = 0,67. Таким образом,
Величину
масштабного коэффициента определяем по кривой 2; при d
=
Характеристика
цикла при кручении 
. Величину допускаемого напряжения для симметричного цикла
при кручении определяем по формуле
Величину
теоретического коэффициента концентрации напряжений при кручении вала с
галтелью находим по таблице. Интерполируя между значениями 
при 
, 
при 
, для отношения 
находим 
. Величина коэффициента чувствительности при
и МПа, равна q = 0,55. Поэтому
Величина масштабного коэффициента та же, что и при изгибе: аМ = 1,46.
Таким образом, допускаемое напряжение для симметричного цикла при кручении равно
Допускаемое
напряжение для постоянного цикла при кручении равно
Величину допускаемого напряжения при кручении детали для цикла с характеристикой r = 0 определяем по формуле
Наибольшие
действительные значения напряжений 
и 
при изгибе и кручении вала равны:
,
и 
Подставив в
условие прочности значения и , а также найденные
Прочность вала обеспечена.
Пример 2.
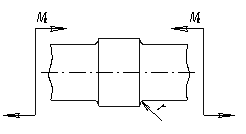
Стальной вал
диаметром 
кНм (см. рис.). В средней
части вал имеет утолщение, причем D/d = 1,25, радиус галтели r = 0,1d. Обработка токарная,
чистовая, материал – сталь 60 с характеристиками: временное сопротивление = 800 МПа, предел
выносливости 
=
300 МПа. Проверить циклическую прочность вала, если коэффициент запаса 
.
Решение.
Условие прочности
при изгибе симметричной нагрузкой 
. Для условий задачи МХmax= 0,2 кНм, 
, 
. Допускаемое напряжение 
где 
предел выносливости
детали.
Из приложений
находим: коэффициент качества поверхности 
= 0,9 (чистовая
обточка, 
, приложение 9), масштабный фактор 
= 0,85 (сталь углеродистая,
= 500...800 МПа, диаметр 
=1,54 (сталь =800 МПа, D/d =1,25, r/d = 0,1, приложение 11). Вычисляем, таким образом, 
, т.е. циклическая прочность обеспечена.
Пример 3.
В опасном
сечении вала с диаметром d
= 35 мм действуют крутящий момент МK = 250 Нм и изгибающий момент Ми = 260 Нм. Вал сделан из
углеродистой стали (предел прочности которой равен 
= 550 МПа, а предел
текучести 
= 260 МПа) и не имеет
резких переходов, выточек, канавок; поверхность его чисто обработана резцом.
Определить коэффициент запаса прочности в опасном сечении вала, приняв нормальные
напряжения изгиба изменяющимися по симметричному циклу, а касательные
напряжения кручения – по пульсирующему циклу.
Коэффициенты
концентрации напряжений и масштабные коэффициенты можно считать одинаковыми для
нормальных и для касательных напряжений.
Решение.
1. Определим максимальные нормальные и максимальные касательные
напряжения
2. По
эмпирическим формулам определим механические характеристики материала:
-
предел текучести при кручении:
МПа;
-
предел выносливости на кручение при симметричном цикле:
МПа;
-
предел выносливости на изгиб при симметричном цикле:
МПа.
3.
Коэффициент концентрации напряжений определим по формуле:
4. Масштабный
коэффициент определим по формуле:
, где d – в сантиметрах.
5.
Коэффициент состояния поверхности берем:
6. Определим
коэффициент запаса прочности по нормальным напряжениям по формуле:
( 
= 0, 
=
= 61,8 МПа, так как имеем симметричный цикл).
По
касательным напряжениям 
= 0.
Так как
касательные напряжения меняются по пульсирующему циклу, то
Тогда по
формуле:
Получим:
7.
Коэффициенты запаса 
и 
по отношению к пределу
текучести равны:
;
Общий коэффициент
запаса прочности по текучести согласно:
Таким
образом, принимаем коэффициент запаса по выносливости n=2,97, т.к. он ниже коэффициента запаса по текучести.
Пример 4.
Определить диаметр вала, если дано: Ми = 4,2 кНм; Мк =3,5 кНм; n0 =3; Rи =0,4; Rкр= -0,7; материал – сталь 40Г; фактор концентрации III, b = 0,05 (полукруглая выточка).
Решение.
1. Определяем диаметр вала из условия
статической прочности:
где Мр – расчётный момент по 3-й теории прочности;
для стали 40Г 
= 360 МПа,
тогда
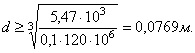
По ГОСТ 6636 – 69 принимаем стандартный диаметр d = 80 мм.
2. Определение коэффициента запаса
прочности.
Механические характеристики для данного материала (сталь 40Г):
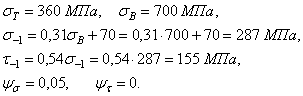
Концентратор – полукруглая выточка. Механическая обработка – грубая шлифовка (назначаем конструктивно).
Из таблиц и графиков приложения любого справочника по сопротивлению материалов найдём коэффициенты учитывающие факторы, которые влияют на предел выносливости:
а) при изгибе
б) при кручении
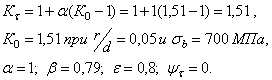
3. Коэффициент запаса прочности по усталости
А. При изгибе
Б. При кручении
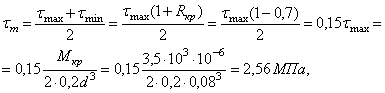
Общий коэффициент запаса:
т.к. условие прочности не выполняется, то определяем новый диаметр
по ГОСТ
6636-69 принимаем dн =
А. При изгибе
где 
= 0,62 (при d =
Б. При кручении
условие прочности выполняется.
Пример 5.
Для
цилиндрической клапанной пружины (рис.1) двигателя внутреннего сгорания
определить коэффициент запаса прочности аналитически (по формуле С.В. Серенсена
и Р.С. Кинасошвили) и проверить его графически по диаграмме предельных
амплитуд, построенной строго в масштабе. Средний диаметр пружины D = 40 мм, диаметр
проволоки пружины d = 4 мм.
Сила, сжимающая пружину в момент открытия клапана 
=240 Н, в момент закрытия клапана 
= 96 Н. Материал проволоки пружины – хромованадиевая сталь с
механическими характеристиками: предел текучести 
= 900 МПа, предел выносливости при симметричном цикле 
=480 МПа, предел выносливости при отнулевом (пульсирующем)
цикле 
= 720 МПа. Для проволоки пружины эффективный коэффициент
концентрации напряжений 
=1,05, коэффициент влияния качества обработки поверхности 
= 0,84, коэффициент влияния абсолютных размеров поперечного
сечения 
= 0,96.
Рис.1
Решение.
1) Определение
максимального 
и минимального 
напряжений в проволоке
пружины и вычисление коэффициента асимметрии цикла R.
Для вычисления напряжений используем формулу
где k – коэффициент, учитывающий влияние поперечной силы и неравномерность распределения напряжений от ее воздействия, а также влияние деформации изгиба вследствие кривизны витков пружины.
Этот коэффициент можно определить по приближенной формуле
где 
- характеристика геометрических параметров пружины.
В данном примере
тогда
Определим величины напряжений:
Коэффициент асимметрии цикла
2) Нахождение среднего (
) и амплитудного (
) напряжений цикла
Найдем
величину среднего и амплитудного
напряжений цикла зависимости от 
:
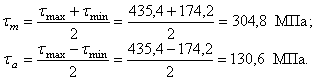
3) Определение коэффициента запаса прочности.
Деталь (пружина) может перейти в предельное состояние по усталости и по пределу текучести.
Коэффициенты запаса прочности по усталости и по пределу текучести определяются по формулам:
где - предел
выносливости при симметричном цикле;
- предел
текучести;
-
коэффициент, учитывающий концентрацию напряжений, влияние качества обработки
поверхности и абсолютных размеров поперечного сечения;
- угловой коэффициент:
Коэффициент запаса прочности по усталости
Коэффициент запаса по пределу текучести
Так как 1,77<2,07, то коэффициент запаса прочности для пружины (по усталости) n = 1,77.
Для анализа
примем силу, сжимающую пружину в момент закрытия клапана, = 180 Н.
Тогда
среднее напряжение
амплитудное напряжение
коэффициент запаса прочности по усталости
коэффициент запаса по пределу текучести
Так как 2,07<2,43, то в этом случае коэффициент запаса прочности (по пределу текучести) n = 2,07.
4) Построение схематизированной диаграммы
предельных амплитуд
Для проверки полученных в п.3 коэффициентов запаса прочности для пружины построим диаграмму предельных амплитуд по методике, предложенной С.В. Серенсеном и Р.С. Кинасошвили (рис. 2).
Порядок построения необходимо описать при выполнении контрольной работы.
Рис. 2
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов
