Главная
Лекция
15 (продолжение). Задачи для самостоятельного
решения
Содержание
Расчеты при инерционных нагрузках
Расчеты при циклических нагрузках
Расчеты на усталостную прочность
Расчеты при инерционных нагрузках
Задача 1.
Между канатом и поднимаемым грузом часто помещают пружину. Для чего это делают?
Задача 2.
Почему резкое торможение барабана грузоподъемника, вызывающее внезапную остановку опускающегося на канате груза, опасно для прочности каната?
Задача 3.
Достаточна ли
прочность троса сечением А=1 см2 для подъема груза массой m=2000 кг, если за первые две
секунды с момента включения лебедки он должен достигнуть высоты h=5 м? Дано: 
Задача 4.
Клеть
шахтного подъемника массой m=2500
кг опускается вниз с постоянной скоростью V=4 м/с. При аварийном заедании троса груз, двигаясь равнозамедленно, достигает крайнего нижнего положения через
0,1 с. Выдержит ли трос в указанной аварийной ситуации, если несущая
способность равна 100 кН?
Задача 5.
Груз
массой 500 кг поднимается равноускоренно вверх на
тросе сечением А=1 см2. При какой величине
ускорения разорвется трос, если предел прочности материала равен 
Задача 6.
Насколько
(в процентах) нужно понизить допускаемое напряжение для того, чтобы расчет
троса, выполненный без учета влияния сил инерции, дал тот же результат, что и
расчет с учетом сил инерции, если ускорение поднимаемого груза равно а=2,5 м/с2?
Задача 7.
Наибольшая
безопасная окружная скорость для чугунных маховиков равна 25 м/с. С каким запасом работает
материал маховиков, если его плотность равна ρ=7,2 т/м3, а
предел прочности на растяжение 
Задача 8.
Имеется
два тонкостенных кольца одинакового веса, одно из которых изготовлено из
дюралюминия (ρ=2,8 т/м3, 
),
а другое из высокопрочной стали 30ХГСА (ρ=7,85 т/м3, 
).
Какое кольцо разорвется при большей окружности равномерного вращения?
Задача 9.
Тонкий
стержень длиной l=1 м и сечением А=1
см2 одним концом прикреплен к горизонтальному валу, а на другом
несет груз массы m.
При вращении вала с угловой скоростью ω=100 рад/с
стержень разорвался. Какова масса груза, если предел прочности материала
стержня равен 
Задача 10.
Скорость вращения маховик за 0,5 с равномерно изменяется с 50 до 30 рад/с. Обод маховика имеет массу m=1000 кг, а радиус инерции его равен 50 см. какие наибольшие касательные напряжения возникают в вале диаметром d=10 см, несущем маховик, вследствие указанного изменения скорости вращения?
Задача 11.
В известном аттракционе «Американские горки» тележка движется по волнообразной трассе. В каких положениях тележка оказывает наибольшее воздействие на опорную конструкцию?
Задача 12.
При
колке дров в полене застрял топор. Как лучше ударить о твердую опору: вниз поленом
или вниз обухом топора, чтобы расколоть полено, масса которого больше массы
топора?
Задача 13.
Груз
массой 500 кг поднимается ускоренно вверх. При каком ускорении подъема разорвется
трос, несущая способность которого равна 15 кН?
Ответ:
а=20 м/с2.
Задача 14.
На
сколько удлиняется буксирный трос жесткостью 100 кН/м при транспортировки автомобиля
массой 2 т с ускорением 0,5 м/с2. Трением
пренебречь.
Ответ:
Δl=1 см.
Задача 15.
Скорость вращения чугунного маховика за 0,1 с равномерно
изменилась с 300 до 290 об/мин. Масса обода маховика равна 1,2 т, а радиус инерции
50 см. Определить величину крутящего момента и наибольшего касательного
напряжения, возникшего вследствие этого изменения скорости в вале, на который
насажен маховик, если диаметр вала равен 80 мм.
Ответ:
Мд=3,14 кНм; 
Задача 16.
Тонкое
стальное кольцо вращается вокруг центральной оси, перпендикулярной его плоскости.
Проверить прочность кольца и определить наибольшую допустимую окружную скорость,
если R=35
см, ρ=7,85 т/м3, n=3000
об/мин, [σ]=100 МПа.
Ответ:
м/с.
Задача 17.
Два
шара массой 5 кг каждый, связанные нитью длиной 1 м и сечением А=0,1 см2, движутся со скоростью V=10 м/с по
горизонтальному столу в направлении, перпендикулярном к связывающей их нити
(нить не провисает). Середина нити налетает на гвоздь. Чему
равны сразу после этого напряжение в нити?
Ответ:
Задача 18.
Кожаный
ремень толщиной 5 мм и сечением А=8 см2
перекинут через шкив диаметром 1 м и передает мощность 40 кВт. Шкив вращается с
постоянной угловой скоростью 100 рад/с. Определить напряжение в ремне без учета
и с учетом сил инерции, если T/t=2, ρ=1 т/м3,
Е=400 МПа.
Ответ:
а) без учета 4 МПа; б) с учетом 6,5 МПа.
Задача 19.
Дюралюминиевый
горизонтальный стержень постоянного поперечного сечения длиной l = 1 м вращается с постоянной
угловой скоростью вокруг вертикальной оси, проходящей через его середину.
Определить для этого стержня предельное число оборотов в минуту, если плотность
материала ρ= 2,8
г/см3, а допускаемое нормальное напряжение Radm = 100 МПа.
Ответ:
nadm = 5100 об/мин.
Задача 20.
Найти наибольшее напряжение в тросе, если при спуске закрепленного
на нем груза весом G=10
кН со скоростью V=10
м/с был включен тормоз, остановивший груз в тот момент, когда длина троса l=5 м. Силу торможения считать постоянной. Площадь
поперечного сечения троса F=2
см2.
Ответ:
.
Задача 21.
Скорость вращения чугунного маховика за 0,1 с равномерно изменилась
с 300 до 290 об/мин. Масса обода маховика равна 1,2т, а радиус инерции 50 см.
Определить величину крутящего момента и наибольшего касательного напряжения,
возникшего вследствие этого изменения скорости в вале, на который насажен
маховик, если диаметр вала равен 80 мм.
Ответ:
Мд=3,14 кНм; τд=31,3 МПа.
Задача 22.
Сплошной
стальной диск одинаковой толщины вращается с постоянной угловой скоростью
ω=200 с-1 вокруг центральной оси, перпендикулярной к его
плоскости. Определить наибольшее нормальное напряжение в диске, если его
диаметр D=90 см.
Ответ:
σд=26,6 Мпа.
Задача 23.
Равномерно
вращающийся вокруг центральной оси, перпендикулярной к его плоскости, стальной
диск постоянной толщины, диаметром D=80 см имеет центральное отверстие диаметром d=10 см. Определить наибольшее
допускаемое число оборотов диска n, при котором максимальное нормальное напряжение в ней не
превысит 
.
Ответ:
n=3410
об/мин.
Задача 24.
Маховик
электроинерционного стартера представляет собой диск
постоянной толщины диаметром D=16
см и весом G=80
Н. за время t=1 сек он приобретает скорость вращения n=8000 об/мин. Найти максимальное
касательное напряжение в вале диаметром d=2 см, на котором насажен маховик. Ускорение считать постоянным.
Ответ:
.
Задача 25.
Стержень
постоянного сечения под действием приложенных сил начинает двигаться с
ускорением а. Постройте эпюру
распределения внутренних усилий, возникающих в стержне.
Задача 26.
Круглый
стержень, несущий посредине груз массы m=1000 кг, поднимается с помощью двух тросов с ускорением а=6 м/с2.
Достаточна ли эта жесткость стержня, если при его равномерном подъеме прогиб
под грузом равен 1 см, а [f]=l/400?
Задача 27.
Закон
движения барабана в период разгона описывается уравнением φ=сt3.
При какой величине с обеспечивается не менее чем трехкратный запас по пределу
прочности в конце первой секунды подъема, если сечение троса 1 см2, а предел прочности материала 
Задача 28.
Вал
диаметром d=50
мм, несущий маховик с моментом инерции Im=10,9
кгм2, в период разгона вращается по закону
φ=30t3.
Какие наибольшие касательные напряжения возникают в поперечном сечении вала в
конце первой секунды его вращения?
Задача 29.
Найти
удлинение однородного стержня длиной l, к которому вдоль оси
приложена сила F.
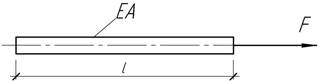
Ответ:
Δl=0,5Fl/EA.
Задача 30.
При
спуске детали с постоянной скоростью V0=6
м/с произошло торможение, при котором в течение 0,5 с
скорость равномерно уменьшилась до V1=1,1
м/с. Найти наибольшее напряжение в детали, если ρ=5 т/м3, l=6
м.
Ответ:
Задача 31.
Определить
напряжения в стержнях 1 и 2 опорной конструкции подъемного устройства,
возникающие при подъеме груза массы m=3
т с ускорением 9,8 м/с2, если А1=8
см2, А2=200 см2.
Ответ:
Задача 32.
Стальной
стержень АВ квадратного сечения 1х1 см, несущий на концах А
и В грузы массой 6 кг, опускается на стальной проволоки с постоянной скоростью
2,4 м/с. Определить прогибы концов стержня, наибольшее нормальное напряжение в
нем, а также напряжение в проволоке, если скорость опускания в течение 0,5 с
равномерно уменьшится в 3 раза. Массой стержня пренебречь.
Ответ:
f=2,4
мм; 
Задача 33.
Подъемный
механизм П весом 20 кН, поднимающий с помощью каната
груз 60 кН, установлен на двух двутавровых балках № 30. Определить натяжение
каната и величину наибольшего нормального напряжения в балках с учетом их
собственного веса и веса подъемного механизма, если груз поднимается
равноускорено и в первую секунду проходит 2,5 м.
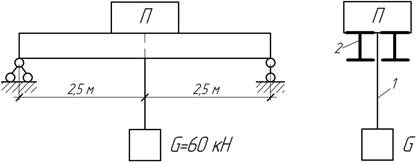
Ответ:
N1=90,6 кН, 
Задача 34.
Противовес
подъемника весит 42 кН. При торможении поднимающегося
подъемника опускающейся противовес испытывает ускорение, равное 1,5 м/с2. Определить диаметр болтов А
и В противовеса, если для материалов болтов [σ]=31 мм, [τ]=20 МПа.
Число болтов: А – два, В – один.
Ответ:
Задача 35.
Груз
массы m=600
кг равноускорено поднимается на тросе сечением А=1 см2.
Определить наибольшее расчетное напряжение в тросе и в опасном сечение вала
диаметром d=6
см по III
гипотезе прочности, если ускорение движения равно 0,8 м/с2.
Массу троса, вала и шкива при расчете не учитывать.
Ответ:
Задача 36.
Регулятор
вращается с постоянной угловой скоростью вокруг вертикальной оси. Считая
стержень АВ абсолютно жестким, найти предельное число оборотов регулятора, а
также соответствующие этому числу оборотов горизонтальное смещение груза, если [σ]=180
МПа. Стержень ВС считать невесомым.
Ответ:
n=104,6
об/мин; 
Задача 37.
Стальной
диск, в котором сделано круглое отверстие, вращается с постоянной угловой
скоростью ω=40 рад/с. Найти
наибольшее нормальное напряжение в вале, вызванное наличием отверстия.
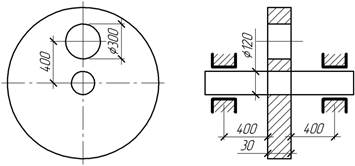
Ответ:
Задача 38.
Круглые
стержни АВ и СД одинакового сечения связаны между собой. Стержень АВ вращается
вокруг вертикальной оси, делая n=300
об/мин. Определить наибольшее напряжение в стержнях, пренебрегая их собственным
весом, если m=1
кг, l=10 см, d=1 см.
Ответ:
Задача 39.
Стержни
АВ и СД прямоугольного сечения жестко заделаны в круглую массивную пластину ВД,
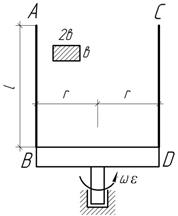
которая вращается в период пуска с постоянным угловым ускорением ε,
достигая в конце этого периода заданной угловой скорости ω. Определить
наибольшее напряжение в стержнях, если плотность материала равна ρ.
Ответ:
Задача 40.
Стальной
ломаный стержень круглого сечения диаметром d=1 см несет на свободном конце груз
массой m=1
кг и вращается равномерно вокруг горизонтальной оси. Пренебрегая массой
стержня, определить наибольшее допускаемое число оборотов из условия прочности
стержня, если [σ]=160 МПа, l=10 см.
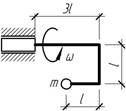
Ответ:
[n]=250
об/мин.
Задача 41.
Рамка
АВСД вращается вокруг вертикальной оси со скоростью n=240 об/мин. Все стержни рамки стальные,
круглого сечения определить диаметр стержней АД и ВС, если [σ]=100 МПа.
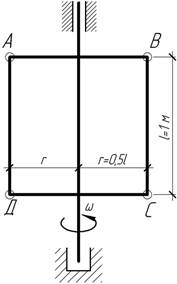
Ответ:
d=25
мм.
Задача 42.
Люлька
качелей, масса которой вместе с людьми равна m=300 кг, подвешена к стальному валу.
Масса люлькой сосредоточена в точке С на расстоянии 4
м от оси вращения. Наибольший угол подъема люльки над горизонтом равен 450.
Определить необходимый диаметр вала, если [σ]=80 МПа.
Ответ:
d=70
мм.
Задача 43.
Определить
наибольшее напряжение в круглых стержнях 1 и 2, пренебрегая их собственным
весом, возникающие при равномерном вращении стержня АВ с угловой скоростью
ω=20 рад/с, если m=3
кг, 
Ответ:
Задача 44.
Определить
угловую скорость вращения, при которой потеряют устойчивость сжатые стальные
стержни.
Ответ:
Задача 45.
Стержни
1, 2 и 3 изготовлены из материала с модулем упругости Е,
имеют одинаковую площадь поперечного сечения А. определить напряжение в стержнях
при вращении системы с угловой скоростью ω. Массой стержня пренебречь.
Ответ:
Задача 46.
Круглые
стержни 1 диаметром 
расположенные вертикально, нижним концом
заделаны в массивную квадратную плиту, а
на верхнем, свободном конце несут грузы массой m=2 кг. Стержни 1 соединены между собой
круглым стержнем 2 диаметром 
Материалы стержней
одинаковы. Определить наибольшие напряжения в стержнях, пренебрегая их массой,
если l=10 см, ω=100 рад/с.
Ответ:
Задача 47.
Круглое
стальное кольцо со средним диаметром D=50
см и диаметром поперечного сечения d=
20 мм вращается вокруг вертикальной оси ОО, совпадающей с диаметром кольца, делая
600 об/мин. Определить наибольшее нормальное напряжение в кольце.
Ответ:
Задача 48.
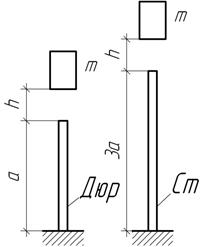
1) Тело, состоящее из двух стальных стержней I и II (рис. 1), движется вверх с ускорением а = 2g. Поперечное сечение стержня I – квадрат со стороной h = 10 см, поперечное сечение стержня II – круг диаметром d = 2,5 см. Длины l1 = 40 см, lII = 80 см. Плотность материала стержней ρ = 7,75 г/см3.
Определить
максимальные нормальные динамические напряжения в каждом стержне.
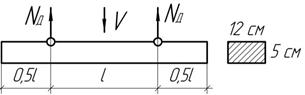
2) Стальной канат длиной l = 20 м с прикрепленным к нему грузом весом Р = 5 кН движется вверх с постоянным ускорением а = g (рис. 2). Рассчитать минимально допустимую (необходимую) площадь поперечного сечения каната, если плотность материала каната ρ= 7,75 г/см3, а допускаемое нормальное напряжение Radm = 30 МПа.
3) Конструкция, состоящая из стержня длиной l = 2 м и площадью поперечного сечения А = 0,0005 м2, вместе с прикрепленными к нему двумя грузами Р1 = 2 кН и Р2 = 4 кН, расстояние между которыми 1 м, движется вверх с постоянным ускорением а = 2g (рис. 3). Определить динамическое удлинение стержня, если модуль упругости материала стержня Е = 0,7∙105 МПа, а плотность ρ= 2,8 г/см3.
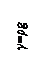
Ответ к рис.1: σmax,I = 0,093 МПа; σmax,II= 2,046 МПа.
Ответ к рис.2: Anec = 3,72 см2.
Ответ к рис.3: ∆ld = 6,9 мм.
Задача 49.
Определить наибольшие нормальные напряжения от изгиба двутавра № 30 длиной l = 10 м, поднимаемого с помощью канатов, прикрепленных в сечениях С и D, с ускорением а, равным 5 м/с2 (см. рис.). Стенка двутавра при подъеме расположена вертикально.
Ответ: σ= 8,58 МПа.
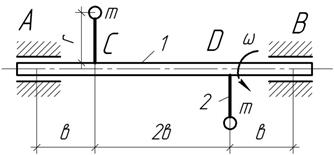
Задача 50.
Определить
наибольшее напряжение в круглых стержнях 1 и 2, пренебрегая их собственным
весом, возникающие при равномерном вращении стержня АВ с угловой скоростью
ω=20 рад/с, если m=3
кг, 
Ответ:
Задача 51.
Определить угловую скорость вращения, при которой потеряют устойчивость сжатые стальные стержни.
Ответ: Пкр=679 об/мин
Задача 52.
Круглые стержни АВ и СD одинакового сечения жестко связаны между собой. Стержень АВ вращается вокруг вертикальной оси, делая П=300 об/мин. Определить наибольшее напряжение в стержнях, пренебрегая их собственным весом, если m=1 кг, l=10 см, d=1 см.
Ответ:
Задача 53.
Рамка
АВСD
вращается вокруг вертикальной оси со скоростью П=240
об/мин. Все стержни рамки стальные, круглого сечения. Определить диаметр
стержней АD
и ВС, если [σ]=100
Мпа, d=25
мм
Задача 54.
Определить
напряжения в стержнях 1 и 2 опорной конструкции подъемного устройства,
возникающие при подъёме груза массы m=3
т с ускорением 9,8 м/с2, если А1=8
см2, А2=200 см2.
Ответ:
Задача 55.
Определить
площадь поперечного сечения троса для подъема контейнера массой m=3,2 т на высоту l=130
м с постоянным ускорением а=2 м/с2. Во время подъема напряжения в тросе не должны
превышать 
плотность материала троса ρ=7,4 т/м3
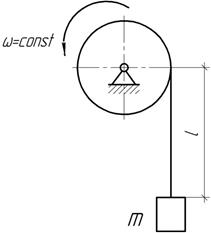
Ответ:
А=2 см2.
Задача 56.
Груз
массы m=2000
кг подвешен на стальном тросе, состоящем из 500 проволок диаметра d=0,5 мм каждая. Барабан
вращается против часовой стрелки с угловым ускорением ε=10 с-2.
Найти нормальное напряжение в тросе. Диаметр барабана D=0,5 м.
Ответ:
Задача 57.
Стальной
ломаный стержень круглого сечения диаметром d=1 см несет на свободном конце груз
массой m=1
кг и вращается равномерно вокруг горизонтальной оси. пренебрегая массой стержня, определить наибольшее
допускаемое число оборотов из условия прочности стержня, если 
.
Ответ:
Задача 58.
Стержни
АВ и СD
прямоугольного сечения жестко заделаны в круглую массивную пластину ВD, которая вращается в
период пуска с постоянным угловым ускорением ε, достигая в конце этого
периода заданной угловой скорости ω. Определить наибольшее напряжение в
стержнях, если плотность материала равна ρ.
Ответ:
Задача 59.
При
спуске детали с постоянной скоростью V0=6
м/с произошло торможение, при котором в течение 0,5 с
скорость равномерно уменьшилась до V1=1,1
м/с. Найти наибольшее напряжение в детали, если ρ=5 т/м3, l=6
м.
Ответ:
Задача 60.
Стержни
1, 2, 3 изготовлены из материала с модулем упругости Е,
имеют одинаковую площадь поперечного сечения А. Определить напряжения в
стержнях при вращении системы с угловой скоростью ω. Массой стержней
пренебречь.
Ответ:
Задача 61.
На
вал диаметром d=100
мм насажен маховик с моментом инерции Im=500
кгм2; скорость вращения вала равна 300
об/мин. Внезапно начинает действовать тормоз, останавливающий маховик через 20
оборотов; вал с маховиком отключаются от двигателя до пуска в ход тормоза.
Определить величину наибольшего касательного напряжения в вале. Трением в
подшипниках пренебречь.
Ответ:
Задача 62.
Тонкое
стальное кольцо вращается вокруг центральной оси, перпендикулярной его
плоскости. Проверить прочность кольца и определить наибольшую допускаемую
скорость. Средний диаметр кольца D=70
см, плотность ρ=7,85 т/м3, частота вращения n=3000 об/мин. 
Ответ:
Задача 63.
Определить
угловую скорость ω равномерного вращения вокруг центральной оси,
перпендикулярной его плоскости тонкого чугунного кольца со средним диаметром D=1,2 м, при которой кольцо может разорваться от действия
центробежных сил. Для чугуна 
плотность ρ=7,2 т/м3.
Ответ:
ω=215 с-1
Задача 64.
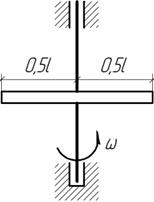
Определить
наибольшие нормальные напряжения и радиальные перемещения концов стального
стержня постоянного сечения длиной l=4 м, вращающегося
вокруг вертикальной оси с постоянной угловой скоростью ω=100 рад/с.
Ответ:
Задача 65,66,67.
Стержневые системы, вращающиеся с постоянной угловой скоростью Ω, показаны на рис. 1-3. Построить эпюры изгибающих моментов Ми от действия инерционных сил и определить допускаемое число оборотов в минуту.
Плотность материала стержней ρ= 7,75 г/см3, поперечные сечения стержней – круглые диаметром d = 3 см, длина отрезка а = 0,2 м, допускаемое нормальное напряжение Radm = 160 МПа.
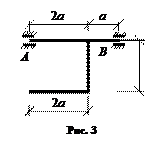
Ответ к рис.1: Mmax=0,75ρAΩ2a3;
Ответ к рис.2: Mmax=ρAΩ2a3;
Ответ к рис.1: Mmax=3ρAΩ2a3.
Расчеты при ударных нагрузках
Задача 1.
Вертикальный стержень, статически растянутый силой F, удлиняется на 1,5 мм. Каково будет удлинение стержня, если тот же груз растянет его, падая с высоты 6 мм?
Задача 2.
По проекту
балка длиной l, воспринимающая удар посредине,
имеет шарнирное закрепление по концам. Как изменится величина наибольших
нормальных напряжений при ударе, если заменить шарнирные опоры заделками7 считать, что высота падения груза много больше
статического прогиба.
Задача 3.
Находящийся в
горизонтальном положении круглый стальной стержень падает с высоты 1 м и
задерживается жесткими опорами по концам. Плотность стали ρ=7,85 т/м3.
Предполагая, что вся энергия падающей балки воспринимается только ею, найти
наибольшее напряжение. Не превосходит ли оно предел пропорциональности
материала, равного 
Задача 4.
При
равномерном опускании груза G=15
кН в результате заедания троса произошла его внезапная остановка. При этом трос
сечением А=5 см2 имел длину l=10
м. какую наибольшую скорость может иметь груз, чтобы исключался обрыв троса в
заданной аварийной ситуации, если [N]=165
кН, Е=75 ГПа? Массой троса пренебречь.
Задача 5.
Повысится
ли комфортность автомобиля, если вместо стальных рессор использовать титановые тех же размеров? Обоснуйте ваше заключение?
Задача 6.
Рессоры легковых автомобилей имеют меньшую жесткость, чем рессоры грузовых автомашин. Чем это объясняется?
Задача 7.
Балка защемлена одним концом, а дрогой конец, нагруженный силой F, подперт колонной, которая внезапно ломается. Чему будет равняться прогиб на конце балки, если жесткость консоли равна с=5 кН/см, F=10 кН?
Задача 8.
Шарнирно опертая по концам балка нагружена посредине сосредоточенной силой F. Как изменится стрела прогиба при внезапном изменении направления нагрузки?
Задача 9.
С какой высоты должен упасть груз на балку, чтобы вызванные ударом напряжения и деформации были в 6 раз больше напряжений и деформаций при статическом действии того же груза?
Задача 10.
Во сколько раз увеличатся динамические напряжения в балке, если высота падения груза возрастет в 4 раза? Считать, что высота падения груза много больше статического прогиба.
Задача 11.
Груз массой m=100 кг, двигаясь горизонтально со скоростью 2 м/с, ударяется о балку, которая при этом прогибается на 4 см. какая статическая нагрузка, приложена в том же сечении балки, вызовет тот же прогиб?
Задача 12.
Груз массы m=2000
кг с постоянной скоростью, равной V0=2,45
м/с, опускается на сматывающем с барабана лебедки тросе.
Когда длина троса между грузом и лебедкой оказывается равной l=140
м, происходит резкое торможение барабана и груз останавливается. Определить
наибольшее нормальное напряжение в тросе и его удлинение без учета его массы,
если приведенный модуль упругости троса Е=70 Гпа, а
его сечение А=4 см2.
Ответ:
Задача 13.
На
стальной вал диаметром d=100
мм насажены два маховика с одинаковыми моментами инерции Im=800
кгм2. Расстояние между маховиками l=3
м. один маховик постоянно заклинен на вале, а другой, свободно вращающийся со
скоростью 30 об/мин,
посредством особого приспособления можно мгновенно сцепить с валом и таким
образом привести в движение всю систему. Определить наибольшее касательное
напряжение в вале в момент сцепления с ним второго маховика.
Ответ:
Задача 14.
Найти
динамическое нормальное напряжение в стальной двутавровой консольной балке (Iz = 2∙10-5 м4,
Wz = 2∙10-4 м3,
Е = 2∙105
МПа) длиной 2 м при ударе по ее свободному концу грузом Р = 1,2 кН, сброшенным с высоты Н = 0,08 м. Собственной массой балки,
испытывающей удар, пренебречь.
Ответ: σd,max = 182 МПа.
Задача 15.
Вычислить, с
какой высоты Н1 падает на
конец консольной балки груз Р = 1,2 кН, если в
защемлении возникает динамическое нормальное напряжение σd,max=
240 МПа. Известно, что при высоте
падения Н = 0,08 м и σst,max= 12 МПа
динамическое напряжение имеет величину σd,max =
182 МПа. Собственной массой балки,
испытывающей удар, пренебречь.
Ответ: Н1 = 0,144 м.
Задача 16.
На конец
стальной консольной балки длиной 1 м с высоты Н = 0,05 м падает груз Р = 480 Н.
Поперечное
сечение балки имеет следующие геометрические характеристики: осевой момент
инерции Iz = 20 000
см4, осевой момент сопротивления Wz =
200 см3. Модуль упругости материала стержня Е = 2·105 МПа. Требуется определить наибольшее нормальное
динамическое напряжение в балке. Собственной массой балки, испытывающей удар,
пренебречь.
Ответ:
σd,max= 120 МПа.
Задача 17.
Груз весом Р = 400 Н падает с высоты Н = 0,3 м на свободный конец консольной
деревянной балки квадратного
поперечного сечения 0,3×0,3 м и длиной 2 м.
Модуль упругости материала балки Е = 104 МПа, его
плотность ρ= 0,6 г/см3. Требуется
определить максимальный динамический прогиб, учитывая собственную массу балки.
Ответ:
∆d,max =
0,0076 м.
Задача 18.
На середину
двутавровой балки № 20 на двух опорах длиной 2 м падает с высоты Н = 0,04 м груз весом Р = 4 кН. Вычислить наибольшие
динамические нормальные напряжения в балке: а) без учета массы балки и б) с
учетом массы балки. Принять Е = 2∙105
МПа.
Ответ: а) σd,max =
209,5 МПа, б) σd,max =
204,1 МПа.
Задача 19.
На конец
стальной консольной балки весом Рб = 250 Н и длиной 1 м с высоты 0,05 м
падает груз Р = 520 Н. Поперечное сечение балки имеет
следующие геометрические характеристики: осевой момент инерции Iz =
20000 см4, осевой момент сопротивления Wz = 200 см3.
Модуль продольной упругости материала балки Е = 2,0∙105
МПа. Требуется определить наибольшее нормальное динамическое напряжение в
балке с учетом ее собственной массы.
Ответ:
σd,max = 120 МПа.
Задача 20.
Груз 4,5 т,
приложенный посредине пролета балки, шарнирно опертой по концам, вызывает
прогиб балки на 2 см. С какой наибольшей скоростью может упасть на эту балку
груз 5 кН, не вызывая прогиба больше 2 см?
Задача 21.
Груз массой m=2000
кг с постоянной скоростью, равной V0=2,45 м/с, опускается на сматывающемся с барабана
лебедки тросе. Когда длина троса между грузом и лебедкой оказывается
равной l=140 м, происходит резкое торможение барабана и груз
останавливается. Определить наибольшее нормальное напряжение в тросе и его удлинение
без учета его массы, если приведенный модуль упругости троса
Е=70 Гпа, а его сечение А=4 см2.
Ответ:
.
Задача 22.
Шарнирно
опертая по концам деревянная балка круглого сечения, длиной 4 м подвергается
посредине пролета удару горизонтально движущимся телом, обладающим в момент
удара кинетической энергией Т=80 Нм.
Определить диаметр балки из условия прочности и жесткости, если [σ]=10 Гпа, [f]=1 см.
Ответ:
d=26
см (из условия жесткости).
Задача 23.
Стальной
стержень диаметром
Ответ: 102 МПа;
Задача 24.
Вертикальный
стержень, статически сжатый силой F, укорачивается на
Ответ:
Задача 25.
Груз
Ответ:
Задача 26.
Груз весом Р = 1 кН падает с высоты Н = 0,04 м на свободный конец консольной
балки прямоугольного сечения 0,12х0,2 м и длиной 2 м. Модуль упругости
материала балки Е = 104 МПа. Требуется
рассчитать наибольшее нормальное напряжение в момент наибольшей деформации
балки. Собственной массой балки, испытывающей удар, пренебречь.
Ответ:
σd,max =
15 МПа.
Задача 27.
Модель
стальной шарнирно опертой балки, изготовленная из той же стали в 1/3 натуральной
величины, была испытана на удар падающим посредине пролета грузом. Нагрузка и
высота ее подъема также были взяты в три раза меньшим, чем в действительной
балке. Динамический коэффициент определенный опытным
путем (из сравнении статической и динамической
деформации модели балки), оказался равным 4. Определить величину динамического
коэффициента в действительной балке в двух вариантах: а) пренебрегая при
расчете собственным весом балки, составляющим 70% веса падающего груза и б)
учитывая этот вес.
Ответ:
а) 6; б) 5,53.
Задача 28.
Шарнирно
опертая по концам деревянная балка круглого сечения, длиной 4 м подвергается
посредине пролета удару горизонтально движущимся телом, обладающим в момент
удара кинетической энергией Т=80 Нм.
Определить диаметр балки из условия прочности и жесткости, если [σ]=10
МПа, [f]=1
см.
Ответ:
d=26
см (из условия жесткости).
Задача 29.
По
проекту балка длиной l, воспринимающая удар
посредине имеет шарнирное закрепление по концам. Как изменится величина
наибольших нормальных напряжений при ударе, если заменить шарнирные опоры
заделками? Считать, что высота падения груза много больше статического прогиба.
Ответ:
Не изменится.
Задача 30.
В каком из двух стержней одинакового поперечного сечения
возникнут большие динамические напряжения?
Задача 31.
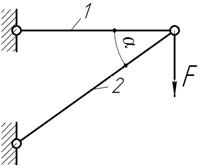
При
статическом приложении силы F
в стержнях кронштейна возникают усилия N1=40 кН и N2=50 кН.
Каким запасом прочности обладает данная конструкция при внезапном, но без удара
приложении силы F?
Дано: А1=4 см2, А2=100
см2, 
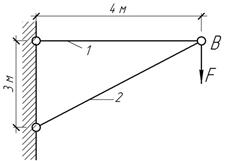
Задача 32.
Сила
F=30
кН мгновенно, но без удара приложена в узле В
кронштейна. Чему равен коэффициент запаса прочности конструкции, если А1=4 см2, А2=100 см2,
Ответ:
n=2.
Задача 33.
Определить
наибольшие касательные напряжения в медном стержне переменного сечения,
возникающие при падении на него груза G=6
кН с высоты 1 см, если а=20 см, А=30
см2.
Ответ:
Задача 34.
Определить
величину наибольшего нормального напряжения в стальном ступенчатом стержне при
ударе падающим грузом массы m=400
кг, если h=12
мм, А=2 см2, а=2 м. На сколько изменится это напряжение, если для смягчения
удара на нижний выступ поместить пружину податливостью α=0,675 мкм/Н.
Принять g=10
м/с2.
Ответ:
уменьшится в 2,5 раза.
Задача 35.
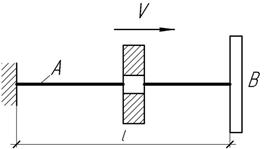
Вдоль
горизонтально расположенного стерня длиной l=1
м и сечением А=5 см2 движется груз, который
достигая выступа В, вызывает продольный удар. Кинетическая энергия груза к
моменту соударения равна Т=32 Нм.
Найти напряжения в стержне при ударе в предположении, что он изготовлен из: а)
стали (Е=200 ГПа); б) дерева (Е=10 ГПа); в) резины (Е=10 МПа).
Ответ:
Задача 36.
Груз
при движении вниз ударяется о груз 
связанный с горизонтально
расположенным стержнем длиной l=50 см и сечением А=4 см2. К моменту соударения груз 
обладает кинетической энергией Т=20 Нм. Определить наибольшее нормальное
напряжение в стержне и его деформацию в двух вариантах: а) при отсутствии груза
;
б) при наличии груза .
Ответ:
а) 
б)
Задача 37.
Сравнить
расчетные напряжения в трех стальных стержнях при ударе грузом G=10 Н, падающим с одной
и той же высоты h=10
см, если l=152 см, А=1 см2.
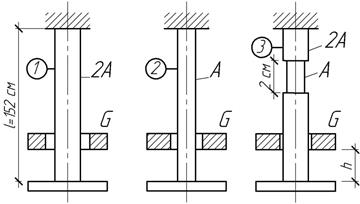
Ответ:
Задача 38.
Крышки
цилиндра крепятся к фланцам с помощью стальных болтов. Вследствие резкого
повышения давления внутри цилиндра болты воспринимают кинетическую энергию
удара Т=6 Нм. Определить
необходимое количество болтов для каждого из двух вариантов крепления, полагая [σ]=50
МПа.
Ответ:
а) 120 шт.; б) 12 шт. на одну крышку.
Задача 39.
Определить
наибольшую высоту падения груза массы m=10
кг из условия прочности стержня ВД, для которого Е=200
Гпа, [σ]=160 МПа, l=1 м, А= 2 см2.
Брус ОС считать абсолютно жестким.
Ответ:
h=12,8
см.
Задача 40.
Груз
G=300
Н, скользя вдоль стержня СД сечением А=20 см2
и длиной l=1,5 м, падает на приваренный к нему
жесткий диск В. Найти перемещение сечения В, а также напряжения на участках ВС
и ВД, названные ударом.
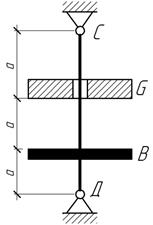
Ответ:
Задача 41.
Кронштейн
выполнен из 3 стальных стержней. При каком значении мгновенно приложенной силы F в одном из стержней
возникнут напряжения, равные пределу пропорциональности 
если
А1=А3=62,5 см2, А2=40
см2.
Ответ:
F=1,3 МН.
Задача 42.
Груз
массой m=50
кг опускается с помощью стального троса, намотанного на шкив
В, со скоростью V0=2
м/с. Когда длина троса оказалось равной 17 м происходит остановка вращения вала
в сечении С. Момент инерции шкива Im=10 кгм2,
приведенный модуль упругости троса равен Е=70 Гпа, а его сечение А=0,2 см2.
Пренебрегая массой шкива, троса и вала, определить наибольшие напряжения в
тросе и в сечении вала.
Ответ:
Задача 43.
Найти
наибольшие нормальные и касательные напряжения для стальной балки без учета ее
массы, если груз массой 40 кг падает с высоты h=4 см.
Ответ:
Задача 44.
Шарик
массой 96 г, двигаясь горизонтально с некоторой скоростью V, ударяется о верхний
конец стального стержня, который прогибается при этом на 1 см. Найти скорость
движения шарика и наибольшее напряжение в стержне.
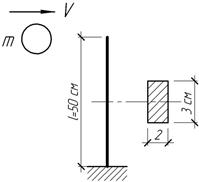
Ответ:
V=10
м/с, σ=240 МПа.
Задача 45.
Проверить
прочность и жесткость деревянной балки, если G=480 Н, а=1 м, h=42
мм, Е=10 Гпа, [σ]=10 МПа, [f]=5
мм.
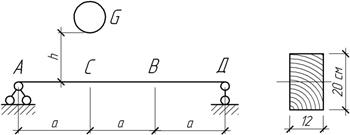
Ответ:
Задача 46.
Пренебрегая
массой балки и пружины, найти прогиб под грузом G=100 Н при его падении с высоты 5 м, если
жесткость пружины с=90 кН/м, жесткость балки ЕI=10 кНм2,
а=1 м.
Ответ:
Задача 47.
Стальная
труба длиной 10 м, наружным диаметром 
(
)
опускается одновременно на две опоры. Найти скорость трубы к моменту удара,
если наибольшее напряжение в трубе равно 160 МПа.
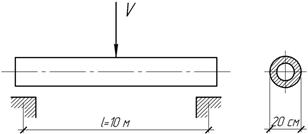
Ответ:
V=1,7 м/с.
Задача 48.
Определить
высоту h
падения груза массой 100 кг, при которой свободный конец консольной балки
двутаврового сечения №16 коснется неподвижной плоскости. Найти также наибольшее
напряжение в балке.
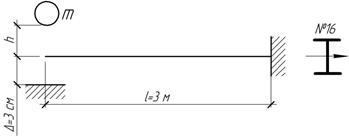
Ответ:
h=6
см, 
Задача 49.
Определить
наибольшие нормальные напряжения и наибольший прогиб балки в 3 вариантах, если
скорость груза к моменту удара равна 0,5 м/с, податливость пружин α=0,4
мкм/Н.
Ответ:
а) 
б) 
в) 
Задача 50.
Стальная
балка заданных размеров не обладает достаточной жесткостью при ударе. Для
уменьшения динамического прогиба предлагается поместить в точке удара пружину. определить наибольшее напряжение
и наибольший прогиб в балке без пружины и установить, какой жесткостью должна
обладать пружина, чтобы обеспечить требуемую жесткость конструкции, если [σ]=200
МПа, [f]=6
мм, h=24
мм.
Ответ:
σ=240 МПа, δ=8 мм, с=6 МН/м.
Задача 51.
Стальной
ломанный стержень квадратного сечения bxb подвергается удару в
точке В грузом массой 2 кг, движущимся со скоростью 4
м/с. Подобрать сечение стержня, если 
а=110
см. При найденных размерах сечения определить наибольшее нормальное напряжение.
Ответ:
b=6
см, σ=99 МПа.
Задача 52.
Определить
наибольшее расчетное напряжение в стальном ломаном стержне ВСД при внезапной
остановке вращения, если m=2
кг, а=20 см, d=2 см, ω=5 с-1.
Использовать третью гипотезу прочности. Собственным весом стержня пренебречь.
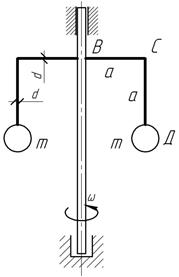
Ответ:
σ=163 МПа.
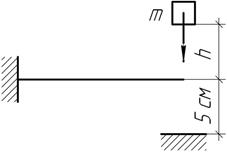
Задача 53.
При какой высоте падения груза массы m=100 кг конец консольной балки жесткостью с=1 кН/см в результате удара коснется неподвижной плоскости?
Задача 54.
Ломанный стержень круглого сечения подвергается действию падающего груза массы m. Чему равно вертикальное перемещение точки В, если G=0,4Е? Дано: Е, I, a, h.
Задача 55.
Вал, несущий маховик с моментом инерции массы Im, вращается с угловой скоростью ω. Насколько будет отличаться наибольшее касательные напряжения в вале при резком зажиме одного и обоих концов?
Задача 56.
Определить
допустимую массу груза, падающего с высоты Н
= 0,1 м на стержень
ступенчатой формы с размерами: l1=
Ответ: Масса груза т =
Задача 57.
Прямой призматический стержень, закрепленный одним концом (см. рис.) и имеющий длину 0,3 м, площадь поперечного сечения 0,0021 м2, на свободном конце принимает удар, кинетическая энергия которого равна 25 Нм. Модуль упругости материала стержня Е = 2,1∙105 МПа.
Определить наибольшее нормальное динамическое напряжение и деформацию. Собственной массой стержня, испытывающего удар, пренебречь.
У к а з а н и е. Задачу решать, считая, что вся кинетическая энергия удара переходит в потенциальную энергию деформации стержня.
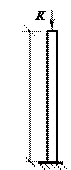
Ответ: σd,max = 100 МПа; ∆ld,max = 0,00024 м.
Задача 58.
Прямой призматический стержень закреплен одним концом (см. рис.), имеет длину 0,3 м, площадь поперечного сечения 0,0021 м2.
Вычислить кинетическую энергию удара и вызываемые им напряжения и деформации стержня, если удар происходит вследствие падения на стержень груза Р = 250 Н с высоты Н = 0,1 м. Модуль упругости материала стержня Е = 2,1∙105 МПа. Собственной массой стержня, испытывающего удар, пренебречь.
Задачу решить:
а) в предположении, что деформацией стержня можно пренебречь по сравнению с высотой Н, и б) не делая упомянутого допущения и вычислив динамический коэффициент.
Ответ: а) σd,max = 100 МПа, ∆ld,max = 0,00024 м;
б) σd,max = 100,1 МПа, ∆ld,max ≈0,00024 м.
Задача 59.
Груз весом Р = 80 Н, скользя без трения вдоль стального бруса (Е = 2∙105 МПа), падает на прикрепленную к брусу жесткую пластину и вызывает ударное растяжение бруса (см. рис. а).
Длина бруса l = 2м, площадь поперечного сечения А = 0,0004 м2; плотность материала бруса ρ= 8 г/см3, расчетное сопротивление стали бруса Rу= 100 МПа. Требуется определить высоту падения бруса: а) без учета массы стержня и б) с учетом массы стержня.
Ответ: а) Н = 0,25 м; б) Н = 0,315 м.
Задача 60.
На чугунную подставку квадратного поперечного сечения 0,3×0,3 м и длиной 1,5 м с высоты Н = 0,4 м падает груз Р = 6 кН. Требуется определить наибольшее нормальное динамическое напряжение в подставке с учетом ее собственной массы. Модуль продольной упругости материала подставки (чугун) Е = 1,27∙105 МПа, плотность чугуна ρ= 7,1 г/см3 (см. рис.).
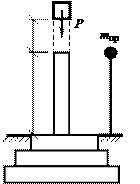
Ответ:
σd,max =
63,9 МПа
Задача 61.
Найти максимальное нормальное динамическое напряжение в канате подъемника (см. рис.), спускающего груз Р = 2∙104 Н со скоростью v =1 м/с при внезапном торможении наверху. Диаметр каната d = 0,02 м, его длина l = 10 м; собственным весом каната пренебречь. Модуль упругости материала каната Е = 1,6∙105 МПа. Жесткость пружины спр = 5∙105 Н/м.
У к а з а н и я
1) Использовать известное из физики соотношение v2 = 2gH.
2) Учесть, что полное статическое перемещение будет складываться из двух частей, связанных с деформацией каната и пружины.
Ответ: σd,max = 181 МПа.
Задача 62.
На
раму квадратного сечения с высоты h=100
мм падает груз G=0,25
кН. Определить наибольшее напряжение в сечении рамы,
если: а=1 м; в=200 мм; 
Задача 63.
Вдоль горизонтально расположенного стержня длиной l=1 м и сечением А=5 см2 движется груз, который достигая выступа В, вызывает продольный удар. Кинетическая энергия груза к моменту соударения равна Т=32 Нм. Найти напряжения в стержне при ударе в предположении, что он изготовлен из: а) стали (Е=200 ГПа); б) дерева (Е=10 ГПа); в) резины (Е=10 МПа).
Ответ:
Задача 64.
Шарик массой
96 г, двигаясь горизонтально с некоторой скоростью V, ударяется о верхний конец стального
стержня, который прогибается при этом на 1 см. Найти скорость движения шарика и
наибольшее напряжение в стержне.
Ответ: V=10 м/с, σ=240 Мпа.
Задача 65.
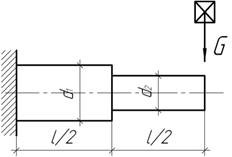
На свободный
конец балки длиной l=1,5 см с высоты h=60 см падает груз G=0,1 кН.
Размеры сечения балки 
Определить наибольшее напряжение и прогиб
балки при ударе.
Задача 66.
Определить
нормальное напряжение в опасном сечении стальной балки, на которую действует
распределенная нагрузка q=4
кН/м и падает груз G=0,4
кН с высоты h=100 мм, если а=0,5 м, 
Задача 67.
При действии
на стальную балку груза G=0,5
кН наибольший динамический прогиб получен равный 20 мм. Определить с какой
высоты h должен падать
груз на балку, если а=0,4 м, 
Задача 68.
Стальная
труба длиной 10 м. наружным диаметром dн=20см (
)
опускается одновременно на две опоры. Найти скорость трубы к моменту удара,
если наибольшее напряжение в трубе равно 160 Мпа.
Ответ: V=1,7 м/с.
Задача 69.
Определить наибольшую высоту падения груза массы m=10 кг из условия прочности ВД, для которого Е=200Гпа, [σ]=160 Мпа, l=1 м, А=2 см2. Брус ОС считать абсолютно жестким.
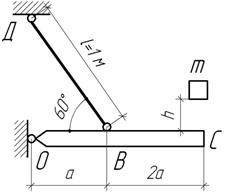
Ответ: h=12,8 см.
Задача 70.
Определить высоту h падения груза массой 100 кг, при которой свободный конец консольной балки двутаврового сечения №16 коснется неподвижной плоскости. Найти также наибольшее напряжение в балке.
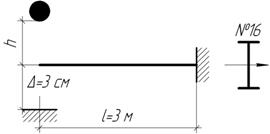
Ответ:
h=6 см,
Задача 71.
Груз G=300Н, скользя вдоль стержня СД сечением А=20 см2 и длиной l=1,5 м, падает на приваренный к нему жесткий диск В. Найти перемещения сечения В, а также напряжения на участках ВС и ВД, вызванные ударом.
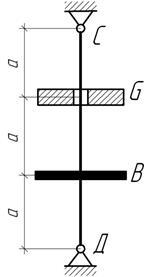
Ответ:
Задача 72.
Кронштейн выполненный из трех стальных стержней. При каком
значении мгновенно приложенной силы F в одном из стержней возникнут напряжения,
равные пределу пропорциональности 
если А1=А3=62,5
см2, А2=40 см2.
Ответ: F=1,3 МН.
Задача 73.
Пренебрегая массой балки и пружины, найти прогиб под грузом G=100 Н при его падении с высоты 5 см, если жесткость пружины С=90 кН/м, жесткость балки EI=10 кНм2, а=1 м.
Ответ:
Задача 74.
Сила F=30 кН мгновенно, но без
удара приложена в узле В кронштейна. Чему равен
коэффициент запаса прочности конструкции, если А1=4
см2, А2=100 см2, 
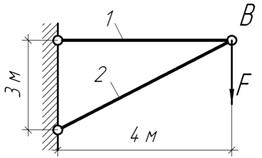
Ответ: П=2
Задача 75.
Определить максимальные напряжения в балке круглого сечения d=50 мм, на которую падает груз G=50 Н с высоты Н=50 мм и действует момент М=1000 Нм.
Задача 76.
Найти наибольшие нормальные и касательные напряжения для стальной балки без учета ее массы, если груз массой 40 кг падает с высоты h=4 см.
Ответ:
Задача 77.
Определить наибольшие касательные напряжения в медном стержне переменного сечения, возникающие при падении на него груза G=6 кН с высоты 1 см, если а=20 см, А=30 см2, Е=100 Гпа.
Ответ:
Задача 78.
Балка АВ прямоугольного
сечения bхh, падая в
горизонтальном положении с высоты H ударяется о балку CD своей серединой. Определить 
в обоих балках, если
сечение их одинаковы. Инерцией балки CD пренебречь.
Расчеты при циклических нагрузках
Задача 1.
Найти массу
груза, подвешенного на резиновом жгуте жесткостью С-250 Н/м, если он совершает
20 колебаний за 16 с.
Ответ: M=4 кг.
Задача 2.
Определить частоту
собственных продольных колебаний: 1) деревянной стойки круглого поперечного
сечения диаметром 15 см и длиной 120 см, нагруженной продольной сжимающей силой
10 т; 2) стальной стойки двутаврового сечения № 20, длиной 1,5 м, сжатой силой
15 т; 3) кирпичного столба квадратного поперечного сечения 80х80 см, высотой
1,8 м, сжатого силой 30 т. Задачу решить без учета массы стоек и столба, нижние
концы их считать защемленными. Для кирпичной кладки принять 
Ответ: 1) 
Задача 3.
Груз, подвешенный на
длинном резиновом жгуте, совершает продольные колебания с
периодом Т. Во сколько раз изменится период колебаний, если отрезать
¾ длины жгута и подвесить на оставшуюся часть тот же груз?
Ответ: уменьшится в 2 раза.
Задача 4.
Спиральная пружина под
действием подвешенного к ней груза растягивается на 6,5 см. Если груз оттянуть
вниз, а затем отпустить, то он начнет совершать продольные вертикальные
колебания. Определить период колебания груза.
Ответ: Т=0,51 с.
Задача 5.
Во сколько раз
изменится частота колебаний автомобиля на рессорах после снятия груза, масса
которого равна массе порожнего автомобиля?
Ответ: увеличится в 1,4 раза.
Задача 6.
Стальной
стержень квадратного сечения 10х10 см растянут силой F=800 кН и предоставлен самому себе.
Какова должна быть длина стержня, чтобы его продольные колебания происходили с
частотой ω=50 рад/с?
Задача 7.
К
стальному и титановому стерням одинаковых размеров подвешен груз массы m=1000 кг. В каком
стержне период собственных вертикальных колебаний будет меньше? Обоснуйте ваше
заключение и дайте количественную оценку.
Задача 8.
Требуется
повысить частоту собственных колебаний упругой системы в 4 раза. Укажите
возможные варианты достижения поставленной цели, рассмотрев, например,
продольные и поперечные колебания круглого стержня постоянного сечения.
Задача 9.
Электромотор,
установленный на балке, может работать в двух режимах вращения ротора: П1=750 об/мин и П2=1500 об/мин. Какой
режим является более опасным с точки зрения прочности балки, если частота
собственных колебаний упругой системы равна 100 рад/с?
Задача 10.
Во
сколько раз изменится амплитуда вынужденных колебаний, если частота вращения
ротора двигателя, установленного на балке, возрастет с 50 рад/с до 200 рад/с? Собственная
частота колебаний упругой системы равна 100 рад/с.
Задача 11.
Ротор
электродвигателя, установленного на балке жесткостью с=1 кН/см, имеет частоту
вращения 50 рад/с. Вследствие неуравновешенности ротора в балке возникают вынужденные
колебания с амплитудой А=4 мм. Чему равна центробежная
сила инерции неуравновешенных масс ротора, если собственная частота колебаний
упругой системы равна 100 рад/с?
Задача 12.
Найти
частоту колебаний груза массой 40 кг, помещенного на балке жесткостью с=16
кН/м.
Ответ:
ω=20 с-1.
Задача 13.
Найти
массу груза, подвешенного на резиновом жгуте жесткостью с=250 Н/м, если он
совершает 20 колебаний за 16 с.
Ответ:
m=4
кг.
Задача 14.
Во
сколько раз изменится частота колебаний автомобиля на рессорах после снятия
груза, масса которого равна массе порожнего автомобиля?
Ответ:
Увеличится в 1,4 раза.
Задача 15.
Груз, подвешенный на длинном резиновом жгуте совершает
продольные колебания с периодом Т. Во сколько раз изменится период колебаний,
если отрезать 3/4 длины жгута и подвесить на оставшуюся часть тот же груз?
Ответ:
Уменьшится в 2 раза.
Задача 16.
Спиральная
пружина под действием подвешенного к ней груза растягивается на 6,5 см. если
груз оттянуть вниз, а затеи отпустить, то он начнет совершать продольные
вертикальные колебания. Определить период колебания груза.
Ответ:
Т=0,51 с.
Задача 17.
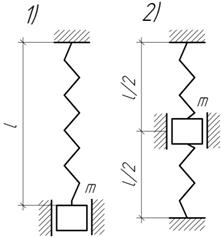
Как
изменится частота собственных колебаний груза, если от первой схемы крепления
перейти ко второй, разрезав пружину на две равные части и закрепив груз
посредине?
Задача 18.
Рассматриваются
две схемы закрепления балки. Во сколько раз изменится частота собственных колебаний
груза при переходе от первой схемы ко второй?
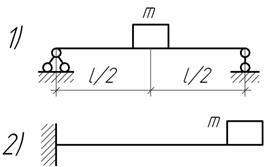
Задача 19.
На
свободный конец консольной балки жесткостью 
предоставленный самому себе, совершает
колебания. Во сколько раз изменится период колебаний
системы, если груз подвесить при помощи пружины, как показано на рисунке?
Пружина вытягивается на 5 мм при нагрузке 1 кН.
Задача 20.
Согласны
ли Вы со следующим утверждением: для увеличения частоты собственных колебаний
груза, укрепленного на собственном конце балки, следует конец консоли опереть
на пружину, как показано на рисунке?
Задача 21.
Ротор
электромотора, установленного на балке, вращается с частотой Ω=80 рад/с. Какова должна быть жесткость
балки, чтобы частота собственных поперечных колебаний системы была на 25% выше
частоты возмущающей силы, возникающей вследствие динамической
неуравновешенности ротора? Масса мотора равна 1000 кг.
Задача 22.
Достаточна
ли жесткость балки, если частота вращения ротора Ω=80 рад/с, а собственная частота колебаний
упруго системы ω=100 рад/с? При работе двигателя массы 500 кг возникает
центробежная сила инерции Fо=900
Н. Жесткость балки с=5 кН/см, а допустимый прогиб [f]=l/600.
Задача 23.
Достаточна
ли прочность данной балки, если частота вращения ротора двигателя Ω=20
рад/с, а собственная частота
колебаний упругой системы ω=30 рад/с? Допускаемое напряжение материала [σ]=160 МПа.
Задача 24.
Определить
круговую частоту ω собственных вертикальных колебаний груза массой 200 кг,
пренебрегая массой стержня АВ (ЕА=40 МН) и абсолютно жесткого бруса СС.
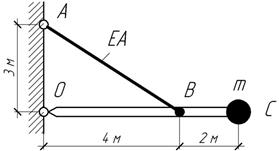
Ответ:
ω=80 с-1.
Задача 25.
Определить
длину стального вала, если для закрепления на нем плоского стального диска
массой 25 кг частота собственных крутильных колебаний в горизонтальной
плоскости равна ω=200 с-1. Массой вала пренебречь.
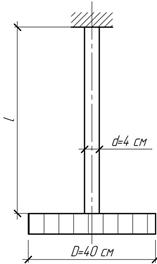
Ответ:
l=1
м.
Задача 26.
Сосредоточенный
груз, помещенный в узле рамы, совершает вертикальные колебания с частотой
ω=50 с-1. Чему равна масса груза, если EI=9 МНм2,
а=3 м?
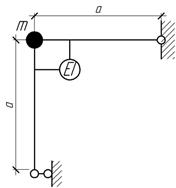
Ответ:
m=200
кг.
Задача 27.
Пренебрегая
массой балки, определить период собственных колебаний груза массы m=200 кг, если жесткость
пружины с=900 кН/м, жесткость балки EI=100
кНм2, а=1
м.
Ответ:
Т=0,314 с.
Задача 28.
Определить
период собственных колебаний системы с одной сосредоточенной массой m=100 кг, если ЕА=200
кН, EI=10
кНм2, а=1
м. Массой балки и стержня пренебречь.
Ответ:
Т=0,14 с.
Задача 29.
Определить
размер а, если период вертикальных
колебаний груза оказался равным Т=0,314 с, а жесткость
EI=1
кНм2. Элемент ОС ломаного стержня ВОС является абсолютно жестким.
Собственной массой системы пренебречь.
Ответ:
а=50 см.
Задача
30.
Определить
период вертикальных колебаний груза m=5
кг, помещенного на свободном конце круглого стального ломаного стержня
диаметром d=2
см, если а=20
см. Массу стержня в расчетах не учитывать.
Ответ:
Т=0,074 с.
Задача 31.
Пренебрегая
массой балки жесткостью EI=90
МНм2, найти частоту собственных колебаний
консоли, несущей на свободном конце груз m=500 кг. На сколько
изменится частота колебаний балки, если концы ее шарнирно закрепить, а груз
поместить посредине пролета.
Ответ:
ω=50 с-1, увеличится в 4 раза.
Задача 32.
Пренебрегая
массой системы, определить частоту колебаний груза массой m=140 кг, если E1I1=250
кНм2, 
м,
Е2А2=21 МН, 
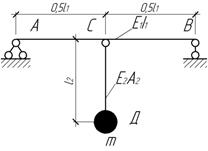
Ответ:
ω=100 с-1.
Задача 33.
Опытным
путем было установлено, что период собственных колебаний груза m=200 кг, расположенного
посредине пролета l=6 м двутавровой балки
№ 24, равен Т=0,35 м. Учитывая массу балки, определить
модуль Юнга материала.
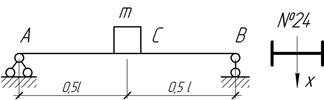
Ответ:
Е=205 ГПа.
Задача 34.
Каменный
столб квадратного поперечного сечения 1,8х1,8 м
опирается на скалу, залегающую на неизвестной глубине от поверхности земли.
Плотность материала кладки равна ρ=2 т/м3. Опытным путем были
определены: а) прогиб верхнего конца столба под действием горизонтальной силы F=60 кН, оказавшийся
равным 4,5 мм; б) период собственных поперечных колебаний столба при снятии
силы F,
равный 0,218 с. Считая столб заделанным в скалу и полагая, что насыпной грунт н
какого влияния на работу столба не оказывает, определить глубину залегания
скалы и модуль упругости материала кладки.
Ответ:
Н=4,5 м, Е=5,9 ГПа.
Задача 35.
Определить
частоту и период угловых колебаний диска диаметра D=60 см и массы m=80 кг, если 
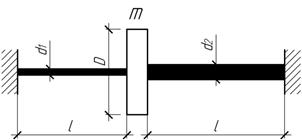
Ответ:
ω=343 с-1; Т=18,3 мс.
Задача 36.
На
каком расстояние а
нужно укрепить массу m,
чтобы частоты собственных вертикальных и горизонтальных колебаний массы
совпадали? Сечения вертикального и горизонтального стержней
одинаковы. Массой стержней пренебречь.
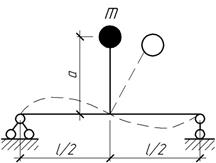
Ответ:
а=0,33l.
Задача 37.
Определить
наибольшее значение возмущающей силы F(t)=F0sin105t, если в режиме
установившихся вынужденных колебаний груза m=500 кг наибольшее нормальное
напряжение в стальной балке равно 116
МПа. Массу балки не учитывать.
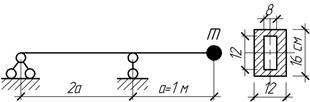
Ответ:
F0=2,4 кН.
Задача 38.
Найти
наибольший угол закручивания жесткостью с=400 Нм,
несущего на свободном конце шкив (Im=4 кгм2), на который действует переменный момент М(t)=40sin9,49t. Массой вала
пренебречь.
Ответ:
Задача 39.
Вычислить
наибольшие нормальные напряжения и прогиб для двутавровой балки (Ix=1800
см4, Wx=180
см3) при работе установленного на ней электродвигателя весом G=5 кН.
Неполная уравновешенность вращающихся частей двигателя с частотой n=300 об/мин приводится
к дисбалансу массой 
с эксцентриситетом е=15 см. Массой балки и влиянием затухания пренебречь.
Ответ:
Задача 40.
Электродвигатель весом G=6
кН, закрепленный на двух швеллерах № 18, делает n=1500 об/мин. Центробежная сила инерции,
возникшая вследствие неуравновешенности ротора, равна F0=1,5
кН. Учитывая собственный вес балок и пренебрегая
силами сопротивления, найти динамический коэффициент и наибольшие нормальные
напряжения в балках.
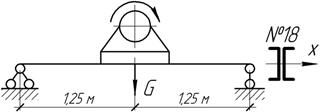
Ответ:
Кд=2,24; 
Задача 41.
Двигатель, делающий 1400 об/мин, укреплен на двух одинаковых
деревянных балках. Подобрать сечение балок с отношением h/b=1,5 так, чтобы частота
собственных колебаний была на 30% больше частоты возмущающей силы, если F0=400
Н, m=160
кг, l=1,4 м, а=0,40 м. определить также наибольшее нормальное напряжение. Массой
балок и силами сопротивления пренебречь.
Ответ:
b=10
см, 
Задача 42.
Двигатель
массой m=900
кг, укрепленный на конце консольной балки из двух уголков 140х140х12, делает n=800 об/мин. При работе
двигателя возникает центробежная сила инерции F0=630 Н.
пренебрегая массой балки, определить наибольшее нормальное напряжение, а
также найти число оборотов двигателя, при котором возникает явление резонанса.
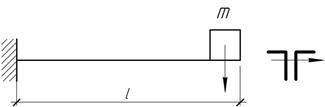
Ответ:
об/мин.
Задача 43.
Найти
амплитуду вынужденных колебаний и наибольшие нормальные напряжения в
двутавровой балке (Iх=1970
см4, h=20 см) если левая опора перемещается в
вертикальном направлении по закону у(t)=12sin38t
мм. Массой балки и влиянием затухания пренебречь.
Ответ:
А=2 мм, 
Задача 44.
На
оси мотора, закрепленного в сечение С стального
стержня ОВ, расположен эксцентрик массой 
на расстояние е=5 см. Зная амплитуду А=0,15 мм
вынужденных колебаний мотора массой m=86 кг (включая массу
эксцентрика), определить число оборотов мотора, пренебрегая массой стержня.
Ответ:
n=2000
об/мин.
Задача 45.
Определить круговую частоту и период свободных изгибных колебаний консольной дюралюминиевой балки круглого сечения и длиной 0,1 м, несущей на конце сосредоточенный груз Р=70 Н. Модуль упругости дюралюминия Е=7∙104 МПа, площадь поперечного сечения балки А=5∙10–6 м2 (см. рис.).
Ответ: ω= 7,65 с–1; Т = 0,82 с.
Задача 46.
Вычислить круговую частоту и период свободных продольных колебаний консольного дюралюминиевого стержня круглого сечения и длиной 0,1 м (см. рис.), размещенного вертикально и несущего на конце сосредоточенный груз Р = 70 Н. Модуль продольной упругости дюралюминия Е = 7∙104 МПа, площадь поперечного сечения стержня А = 5∙10–6 м2.
Ответ: ω= 700 с–1 ; Т = 0,009 с.
Задача 47.
Вычислить круговую частоту и период свободных изгибных колебаний консольной стальной балки квадратного поперечного сечения со стороной а = 0,02 м и длиной 0,5 м (см. рис.), несущей на конце сосредоточенный груз весом Р = 160 Н. Модуль продольной упругости стали Е = 2∙105 МПа.
Ответ: ω = 62,8 с–1; Т = 0,1 с.
Задача 48.
На невесомой балке (см. рис.) пролетом l = 5 м находится двигатель массой m = 2000 кг на расстоянии а = 2 м от левой опоры. Определить круговую частоту и период свободных колебаний системы, если сечение балки – двутавр № 24, модуль упругости материала балки Е = 2∙105 МПа.
Ответ: ω = 40 с–1; Т = 0,157 с.
Задача 49.
Определить
круговую частоту и период свободных продольных колебаний стержня круглого
переменного сечения, к нижнему концу которого прикреплен груз весом Р = 40 кН (рис. 1). Диаметры по участкам равны: d1 =
0,02 м; d2 =
0,03 м; d3 = 0,04 м. Длины
участков l1 = 0,5 м; l2 = 0,75 м;
l3 = 1,0 м. Весом стержня пренебречь. Модуль
упругости материала балки Е = 2∙105
МПа.
Ответ: ω= 120 с–1; Т = 0,0523 с.
Задача 50.
Определить круговую частоту и период свободных продольных колебаний стального стержня с площадью поперечного сечения А = 0,008 м2 и длиной участков l1 = 0,4 м, l2 = 0,6 м, несущего на конце массу mг = 200 кг (см. рис.). Модуль продольной упругости стали Е = 2∙105 МПа, ее плотность ρ= 7,75 г/см3 . В расчете учесть собственную массу стержня.
У к а з а н и е. Учесть, что в данной системе имеет место параллельное соединение упругих связей.
Ответ: ω= 1744 с–1; Т = 0,0036 с.
Задача 51.
Определить круговую частоту и период свободных изгибных колебаний консольной дюралюминиевой балки круглого поперечного сечения диаметром d=5 см и длиной l=2 м, несущей на конце сосредоточенную массу mг = 20 кг. Модуль упругости дюралюминия Е = 7∙104 МПа, его плотность ρ= 2,8 г/см3 (см. рис.).
В расчете учесть собственную массу балки.
Ответ: ω = 18,8 с–1; Т = 0,33 с.
Задача 52.
Определить круговую частоту и период свободных изгибных колебаний однопролетной дюралюминиевой балки круглого поперечного сечения диаметром d =5 см и длиной l =2 м, несущей посередине сосредоточенную массу mг =20 кг (см. рис.). Модуль упругости дюралюминия Е = 7∙104 МПа, плотность ρ= 2,8 г/см3.
В расчете учесть собственную массу балки.
Ответ: ω = 71 с–1; Т = 0,088 с.
Расчеты на усталостную прочность
Задача 1.
Чему равен
предел выносливости, если амплитуда предельного цикла равна 
а коэффициент асимметрии составляет 
Задача 2.
Ступенчатый
вал с размерами D=60
мм, d=50
мм, r/d=0,05, должен работать
в пресной воде на знакопеременное кручение по симметричному циклу с
коэффициентом запаса [n]=1,5.
Установить, какой вал обладает большей несущей способностью: из стали 5, для
которой 
из стали 40Х, для которой 
Ответ:
Несущая способность валов одинаковая.
Задача 3.
Деталь
изготовлена из стали 45 и работает на переменной растяжение и кручение. проверить
прочность детали, если 
Ответ:
Задача 4.
Стальной
ступенчатый вал круглого сечения диаметрами D=60 мм, d=50 мм и радиусами переходной галтели r=5 мм подвергается
действию переменного изгиба и кручения. С каким запасом прочности работает вал,
если в опасном переходном сечении имеет: от изгиба – Mmax=4
кНм, Mmin=2 кНм;
от кручения - MКmax=3 кНм,
MКmin=1 кНм.
Вал изготовлен из стали 12ХНЗА, его поверхность отшлифована и подвергнута
упрочнению с Кv=1,3.
Ответ:
n=1,5.
Задача 5.
Определить
запас прочности ступенчатого вала с диаметрами D=48 мм, d=40 мм, радиусом r=2 мм, испытывающий переменный изгиб с
кручением. Нормальные напряжения изменяются от 
до 
касательные – от 
до 
.
Материал – легированная сталь, для которой 
Поверхность вала тонко обточена. Как изменится
запас прочности, если поверхность вала подвергнуть полированию?
Ответ:
,
т.е. увеличится на 10%.
Задача 6.
Постройте
схематизированную диаграмму Серенсена-Кинасошвили для
стали 45Г2 (
)
и определите по ней графоаналитически коэффициент запаса прочности
детали, работающей на изгиб, в опасной точке которой нормальные напряжения
изменяются от 
Принять К=2.
Задача 7.
Две
одинаковые детали работают на растяжение-сжатие при различных циклах изменения напряжений:
в опасном сечении первой детали 
для второй - 
Материал деталей сталь 20, для которой 
Какая деталь работает с большим коэффициентом
запаса прочности? выполните количественную оценку, приняв К=1,4.
Задача 8.
Вал
испытывает совместное действие изгиба и кручения. Достаточно ли прочность
данного вала, если запасы прочности по нормальным и касательным напряжениям
соответственно равны Пб=1,9 и Пτ=10,
а нормативный коэффициент запаса прочности детали должна быть не менее [П]=2?
Задача 9.
Какой
вал обладает большей надежностью, если парциальные запасы по нормальным и
касательным напряжениям соответственно равны: 1-й вал - Пб=4, Пτ=3; 2-й вал - Пб=2,5
и Пτ=8,6? Обоснуйте ваше заключение и
выполните количественную оценку.
Задача 10.
Определить
для стали, кривая предельных амплитуд которой
(при рассматриваемых циклах 
)
приближенно описывается уравнением 
.
Ответ:
Задача 11.
С
каким запасом прочности работает ступенчатый вал, нагруженный изгибающим моментом,
изменяющийся по симметричному циклу, если Мmax=300 Нм, D=48
мм, d=40
мм, r=2
мм, 
поверхность
вала тонко обточена.
Ответ:
Задача 12.
По
заданной диаграмме предельных амплитуд определите ориентировочно пределы
выносливости и коэффициент асимметрии цикла, для которого среднее напряжение 
Задача 13.
Определите
предел выносливости шлифованной детали, изготовленной из стали 40ХН.
Поверхность детали подвергнута обдувке дробью (КV=1,25).
Продольная сила изменяется по симметричному циклу. Для самопроверки сравните
результаты ваших вычислений с приведенными ниже данными: 
Задача 14.
Балка
нагружена силой F,
изменяющейся по симметричному циклу. По какому сечению произойдет разрушение
балки, если К1=1,4; К2=2,1; К3=1,9?
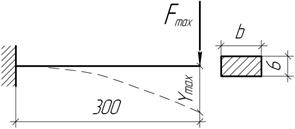
Задача 15.
С
каким запасом прочности работает балка, нагруженная силой F, изменяющейся по
пульсационному циклу, если наибольший прогиб равен Vmax=1
см? балка изготовлена из стали 40ХН. Для опорного сечения принять К=2,9.
Задача 16.
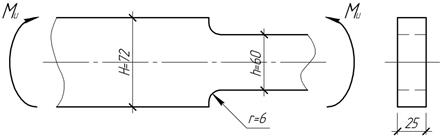
Балка
прямоугольного сечения, изготовленная из стали 12ХНЗА (
),
в плоскости наибольшей жесткости подвергается действию переменного изгибающего
момента Ми. Принимая запас прочности равным [П]=1,9, определите
наибольшую допускаемую величину Мmax,
если отношение моментов Мmin/Мmax=-0,5, а К=4.
Задача 17.
Насколько
повысится несущая способность полированного вала, нагруженного переменным
крутящим моментом, изменяющимся по симметричному циклу, если радиус закругления
галтели увеличить с 
Принять 
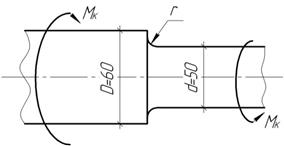
Задача 18.
Ступенчатый
стержень круглого сечения изготовлен из стали 20Х, для которой 
В галтелях 
Поверхность тщательно полирована.
Определить коэффициент запаса прочности, с которым работает стержень при переменной
осевой силе, изменяющейся по симметричному циклу с Fmax=
- Fmin=60
кН.
Ответ:
n=1,58.
Задача 19.
Деталь,
изготовленная из стали 45, должна работать при знакопеременной изгибе с амплитудой 
при коэффициенте запаса прочности [n]=2. Каким должен быть
коэффициент асимметрии цикла Rσ,
если поверхность детали отшлифована и подвергнута упрочнению с Кv=1,19.
Ответ:
Rσ=0,25.
Задача 20.
Деталь
изготовлена из стали 35 и работает на переменное растяжение-сжатие при характеристике
цикла Rσ=-0,4
с коэффициентом запаса прочности, равным [n]=1,6. Поверхность детали тонко обточена
и подвергнута упрочнению с Кv=1,32. Определить
наибольшее допускаемое напряжение максимального напряжения цикла.
Ответ:
Задача 21.
Стальной
вал с тщательно полированной поверхностью, имеющий сквозное поперечное круглое
отверстие, должен работать при пульсационном цикле с коэффициентом запаса [n]=1,8. Определить
допускаемое значение максимального крутящего момента, если 
Кv=1,2.
Принять Wк=Wр(1-a/d).
Ответ:
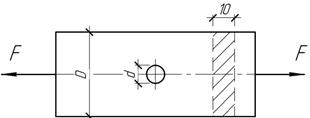
Задача 22.
Найти запас прочности тонко обточенной пластины 10х100 мм с
поперечным отверстием диаметром d=20
мм, если под действием циклических осевых сил продольные деформации,
определенные на достаточном удаление от концентратора напряжений, изменяются по
пульсационному циклу с 
. Материал – сталь 35.
Ответ:
n=3,12.
Задача 23.
Определить
допускаемое значение амплитуды крутящего момента, изменяющегося по
симметричному циклу, если шлифованный вал изготовлен из стали 60, [n]=2, для опорных сечений
КF=0,92;
Кv=1,29.
Ответ:
[Ма]=1 кНм.
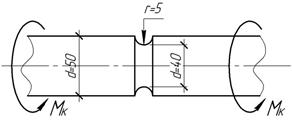
Задача 24.
Найти
запас прочности шлифованного вала, изготовленного из стали 45 и нагруженного
крутящим моментом, изменяющимся по пульсационному циклу, если максимальный
относительный угол закручивания для его неослабленной части равен 
мрад/м.
Ответ:
n=2,2.
Задача 25.
Определить
диаметр круглого стержня, ослабленного круглым отверстием и нагруженного осевой
силой, изменяющейся по симметричному циклу, если a/d=0,1, Fmax=100
кН, [n]=1,5;
поверхность
стержня грубо обточена.
Ответ:
d=50
мм.
Задача 26.
Определить
поперечные размеры ступенчатого вала, нагруженного переменным крутящим моментом,
изменяющимся по пульсационному циклу, если Мmax=850 Нм, D/d=4/3, r/d
=0,1; [n]=1,8.
Материал – сталь 40ХН. Поверхность вала шлифована.
Ответ:
d=30
мм.
Задача 27.
Стержень
прямоугольного сечения с галтелью, изготовленный из стали 35, подвергается
действию сжимающей нагрузки, величина которой меняется от 0,15Fmax до Fmax.
Определит наибольшую допускаемую величину Fmax,
если Н=45 мм, h=30
мм, r=6
мм, b=20
мм, [n]=1,7.
Поверхность детали грубо обточена.
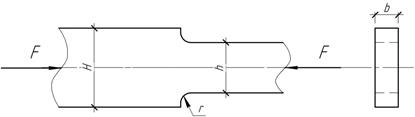
Ответ:
[Fmax]=68 кН.
Задача 28.
Определить
коэффициент запаса прочности двутавровой балки № 20, нагруженной постоянной
равномерно распределенной нагрузкой интенсивности q=18 кН/м и переменной сосредоточенной
силой F,
изменяющейся от 0 до 17 кН. Принять 
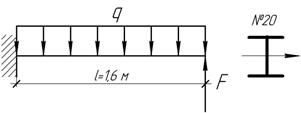
Ответ:
[n]=1,5.
Задача 29.
Балка
нагружена постоянной силой F1=0,8F и переменной F2,
величина которой меняется от 0 до F.
Определить допускаемое значение [F],
если [n]=1,8;
К=1,6 и для материала балки 
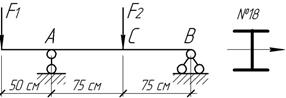
Ответ:
[F]=50
кН.
Задача 30.
Стальная
балка ослабленная сквозным отверстием, нагружена
статически приложенной силой F.
Материал – сталь 45. Найти допустимое значение силы F, обеспечив трехкратный запас по пределу
текучести. Принимая найденное значение за Fmax,
установить, с каким запасом прочности будет работать балка при изменение F по пульсационному
циклу, если КF=0,89;
Кv=1.
Ответ:
[F]=10
кН, n=2.
Задача 31.
Круглый
ступенчатый стержень изготовлен из сталь 35.
Поверхность его отшлифована и подвергнута наклепу Кv=1,17.
Требуется: 1) найти допустимое значение силы F при расчете на переменную нагрузку,
изменяющуюся по симметричному циклу с запасом прочности [n]=1,5; 2) считая
найденную нагрузку статической, определить запас прочности по пределу
текучести.
Ответ:
[F]=1
кН, 
Задача 32.
Балка
прямоугольного сечения, ослабленная выточками, подвергается действию изгибающего
момента, изменяющегося от -0,5Мmax до + Мmax. Балка изготовлена из
стали 20 и повергнута шлифованию. Определить допустимое значение максимального
момента [Мmax], если Н=90 мм, h=60 мм, r=3 мм, b=25 мм, [n]=1,5. На сколько
изменится несущая способность балки, если увеличить радиус закругления до 6 мм,
подвергнуть балку полированию и поверхностному наклепу путем обдувки дробью с Кv=1,25?
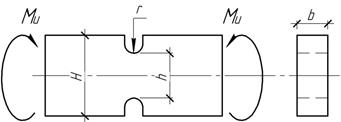
Ответ:
[Мmax]=823
Нм; увеличиться на 57%.
Задача 33.
Определить
допускаемое значение максимального крутящего момента, приложенного к
ступенчатому валу, если Мmin /Мmax=0,25; D=80 мм, d=60 мм, r=3 мм, [n]=2; материал – сталь
60, поверхность шлифована.
Ответ:
[Мmax]=5
кНм.
Задача 34.
Балка
круглого поперечного сечения, ослабленная круглым поперечным отверстием,
подвергается действию изгибающего момента, меняющегося от 1 кНм
до 2,5 кНм. Поверхность балки тонко обточена,
материал – сталь 60. Определить запас прочности, приняв 
Ответ:
Задача 35.
Стальной
стержень подвергается действию переменной осевой силы, изменяющейся по
симметричному циклу с Fmax=15 кН.
Определить минимальный радиус переходного закругления r, если 
Ответ:
r=3
мм.
Задача 36.
Определить
допускаемое значение амплитуды силы F,
изменяющейся по симметричному циклу, если К1=1,4;
К2=2,1; К3=1,9; 
Ответ:
[Fa]=10
кН.
Задача 37.
Определить
запас прочности вала диаметром d=50
мм, на который напрессована втулка, если изгибающий момент изменяется по
симметричному циклу с Мmax=750
Нм, поверхность вала полирована, 
давление
напрессовки р=35 МПа.
Ответ:
n=1,49.
Задача 38.
Проверить
прочность детали, нагруженной постоянной силой F0=2
кН и переменной силой F,
изменяющейся по симметричному циклу с Fmax=1
кН, если D=80
мм, d=40
мм, r=2
мм, l=40
см, a=10 см, [n]=2; материал детали – сталь
60.Поверхность детали грубо обточена.
Ответ:
n=2,17>[n], т.е. прочность
обеспечена.
Задача 39.
Найди
допускаемое значение амплитуды силы F,
изменяющейся по симметричному циклу, для полирования детали, изготовленной из
стали 35, полагая [n]=2.
Ответ:
[Fa]=10
кН.
Задача 40.
Определить
запас прочности шлифованного вала с кольцевой выточкой, изготовленного из стали
20. При установки на вал шкивов и внутренних колец подшипников в опорных
сечения давление посадки р=16 МПа. Дано: D=50 мм, d=40 мм, r=5 мм, R=50 см, F=1 кН.
Ответ:
Задача 41.
Определить
минимальный радиус галтели для ступенчатого вала с диаметром d =35 мм, D =
Ответ: Минимальный радиус закругления r = 1,75 мм.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов
