Изгиб

Изгибом называется вид нагружения бруса, при котором к нему прикладывается поперечная нагрузка, лежащая в плоскости проходящей через продольную ось (рис.6.1, а). В этой же плоскости располагается изогнутая ось стержня (упругая линия) (рис.6.1, б). Брус, работающий при изгибе, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90°, называется рамой.

Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).

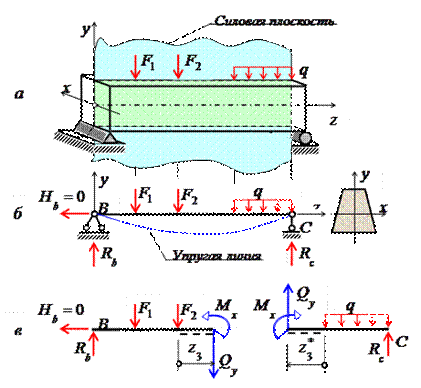
Рис.6.1

При плоском поперечном изгибе в балке возникают два вида внутренних усилий (рис.6.1,в): поперечная сила Q_y , где y – ось симметрии (главная центральная ось) и изгибающий момент M_x. , где x – другая главная центральная ось сечения, нормальная к оси симметрии. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.

Если изгибающий момент M_x является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы Q_y изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.

Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.

Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.

Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.

Рис.6.2

Осваивать расчет балок и рам удобно, рассматривая по очереди следующие вопросы:

- Определение внутренних усилий в балках и построение эпюр внутренних усилий.

- Проверка прочности балок.

- Определение перемещений и проверка жесткости балок.

Решение этих вопросов получим в соответствующих разделах на примере конкретных задач.

Механические испытания на изгиб

Испытания на изгиб часто используются для оценки механических свойств материалов в хрупком или малопластичном состоянии, при воздействии коррозионной среды (коррозии под напряжением), а также для оценки пластичности и качества сварных соединений. Испытание на изгиб воспроизводит характерные для многих конструктивных элементов условия механического нагружения и позволяет выявить свойства поверхностных слоев, наиболее напряженных при разрушении.

Чаще всего образцы нагружают по схемам так называемого трехточечного (рис.6.3,а) и четырехточечного (рис.6.3,б) изгиба.

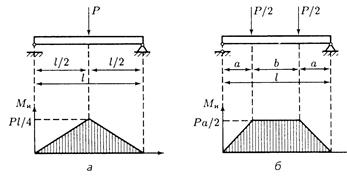
Ocr0196

Рис.6.3

Результаты испытания на изгиб представляются в виде диаграммы P-f, где P- изгибающая нагрузка, f - стрела прогиба образца. Характерные диаграммы изгиба для хрупких (малопластичных) и пластичных материалов приведены на рис.6.4. Для хрупких материалов последняя точка диаграммы соответствует разрушению без практически остаточных деформаций. По разрушающей нагрузке определяют предел прочности материала при изгибе . Пластичные материалы, как правило, невозможно довести до разрушения: образец изгибается до состояния, когда его части располагаются параллельно друг другу.

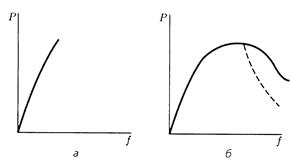
Ocr0197

Рис.6.4

При испытании пластичных материалов можно определить сопротивление материала начальным пластическим деформациям, воспользовавшись методикой, аналогичной применяемой при растяжении для определения соответствующих характеристик, без учета пластического перераспределения напряжений в процессе изгиба.

Построение эпюр поперечной силы и изгибающего момента

Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.

Эпюра внутренней силы – график, показывающий изменение этой силы по длине балки.

Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.

Последовательно на каждом участке вводится скользящая система координатных осей (начало координат совмещается с началом участка) и для произвольного сечения составляются выражения для определения поперечной силы и изгибающего момента. Затем по этим выражениям в пределах каждого участка строятся графики (эпюры) внутренних сил.

Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 6.5 показаны эти закрепления. Для неподвижной (рис 6.5,б) и подвижной (рис. 6.5,в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.5,а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 6.3,б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.6.5,в).

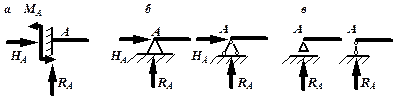
Рис. 6.5. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;

в – в шарнирно-подвижной опоре

Комбинируя различные типы закреплений, можно получить ряд схем балок:

1. Балка шарнирно опертая по концам (рис.6.6,а). Одна опора шарнирно подвижная, другая – шарнирно неподвижная. Расстояние между центрами опор на схеме называется пролетом. Число реакций равно трем. Учитывая, что для плоской системы сил можно составить три независимых уравнения равновесия системы в целом, приходим к заключению, что балка статически определимая.

2. Балка шарнирно опертая с консолями (С₁ и С₂) (рис.6.6,б). Реакции те же. Балка статически определимая.

3. Балка жестко закрепленная одним концом (консольная балка) (рис.6.6,в). В заделке три реакции. Балка статически определимая. При действии нагрузки перпендикулярной оси реакция Н_В всегда равна 0.

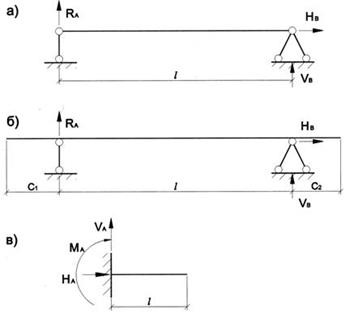
Рис.6.6

После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.

Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).

Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.

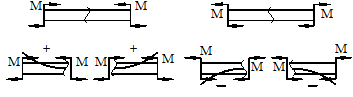
а) б)

Рис.6.7. а - правило знаков для поперечной силы Q; б - правило знаков для изгибающего момента M.

Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.

Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.

Достаточно очевидно и подтверждается опытом, что балка при изгибе деформируется таким образом, что волокна, расположенные в выпуклой части, растягиваются, а в вогнутой – сжимаются. Между ними лежит слой волокон, который лишь искривляется, не изменяя своей первоначальной длины (рис.6.8). Этот слой называется нейтральным или нулевым, а его след на плоскости поперечного сечения – нейтральной (нулевой) линией или осью.

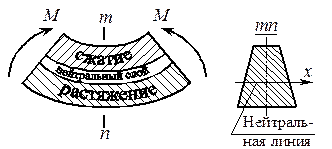
Рис.6.8

При построении эпюр Q и М договоримся на эпюре Q положительные значения откладывать сверху нулевой линии. На эпюре М у строителей принято откладывать положительные ординаты снизу. Такое правило построения эпюры М называется построением эпюры со стороны растянутых волокон, т. е. положительные значения М откладываются в сторону выпуклости изогнутой балки.

Рассмотрим для простоты балку с прямоугольным поперечным сечением (рис.6.9). Следуя методу сечений, мысленно проведем разрез и отбросим какую-либо часть балки, а другую оставим. На оставшейся части покажем действующие на нее силы и в поперечном сечении – внутренние силовые факторы, которые являются результатом приведения к центру сечения сил, действующих на отброшенную часть. Учитывая, что внешние силы и распределенные нагрузки лежат в одной плоскости и действуют перпендикулярно оси балки, в сечении получим поперечную силу Q_y и изгибающий момент M_x. Эти внутренние силовые факторы заранее неизвестны, поэтому их показывают в положительном направлении в соответствии с принятыми правилами знаков.

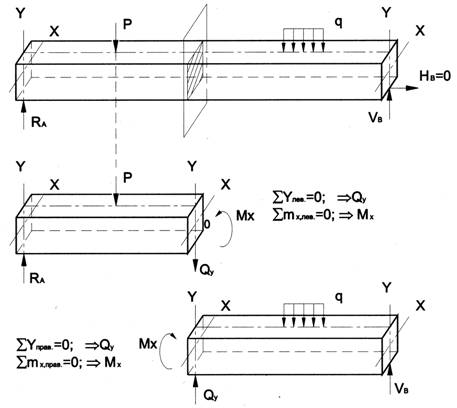
Рис.6.9

На рис.6.9 показаны два случая оставшейся части: левая и правая.

Для определения величины Q_y и M_x составляются два уравнения равновесия для оставшейся части

Изгибающий момент M_x, действующий в поперечном сечении балки, по величине равен сумме моментов всех внешних сил, приложенных к рассматриваемой отсеченной части бруса, относительно центральной оси x этого сечения:

Если внешняя сила в данном сечении растягивает нижние волокна балки, то момент этой силы в этом сечении считается положительным, если растягиваются верхние волокна балки, то момент этой силы будет отрицательным.

Поперечная сила Q_y в сечении бруса, по величине равна сумме проекций всех внешних сил, действующих на отсеченную часть бруса, на ось перпендикулярную оси бруса (ось y):

Уравнение момента составляется относительно оси Х, проходящей в поперечном сечении через точку на оси балки – тогда поперечная сила в уравнение не входит и величина M_x определяется независимо от Q_y. Можно доказать, что результат вычислений Q_y и M_x не зависит от того, равновесие какой оставшейся части рассматривается.

Рассмотрим характерный пример (рис. 6.10,а) и установим необходимые правила. Решение задачи, как правило, начинается с определения полной системы внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями (рис. 6.10,б), выполняющими ту же роль, что и опорные закрепления.

Заданная система статически определима, следовательно, из условий равновесия системы, т.е. равенства нулю суммы моментов всех сил относительно шарнирных опор (в шарнирах нет ограничений поворота сечений балки, поэтому изгибающих моментов не возникает) и , определяем вертикальные реакции в опорах:

Для определения имеем: откуда . Для проверки правильности вычислений воспользуемся условием равенства нулю суммы всех вертикальных сил откуда получим

0 = 0.

Рис. 6.10

Для определения внутренних силовых факторов - изгибающего момента М(z) и поперечной силы Q(z) как функций от продольной координаты z, воспользуемся методом сечений. Для получения этих зависимостей балку разбивают на участки, границами которых являются следующие точки: начало и конец балки; точки приложения сосредоточенных усилий; начало и конец действия распределенных усилий; сечения, в которых скачкообразно изменяется жесткость балки; в точках, где происходит изменение ориентации элементов, если имеем дело с стержневой системой со сложной структурой.

Заданная система состоит из двух участков - первого (0≤z≤a) и второго (a≤z≤a+b). Следовательно, задавая последовательно сечения, принадлежащие к первому и второму участкам, и рассматривая равновесие отсеченных частей системы при действии на них всех внешних сил и внутренних усилий, определим выражения для внутренних силовых факторов.

Из условия равновесия отсеченной части системы, расположенной левее от сечения z₁ (первый участок), (см. рис. 6.10, в), получим:

Для определения Q_y и M_x на втором участке рассмотрим равновесие отсеченной части балки, расположенной правее от сечения z₂ (см. рис. 6.10, б), т.е. откуда и определим:

Эпюры Q_y и M_x изображены на рис. 6.11. Заметим, что эпюры изгибающих моментов M_x, как и поперечных сил Q_y строятся на оси бруса, однако в отличие от эпюры поперечных сил знак момента не указывается, а ординаты изгибающего момента откладываются co стороны растянутых волокон.

Рис. 6.11

Основные дифференциальные соотношения теории изгиба

Пусть брус нагружен произвольным образом распределенной нагрузкой q=f(z) (рис. 6.12,а).

Рис. 6.12

Выделим из бруса элемент длиной dz и приложим по его краям положительные внутренние усилия (рис. 6.12,б). В пределах малого отрезка dz нагрузку q можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, проходящей через точку С (рис. 6.12,б), получим:

Производя упрощения и отбрасывая величины высшего порядка малости, получим теорему Журавского (теорему Шведлера):

откуда

Указанные дифференциальные зависимости при изгибе позволяют установить некоторые особенности эпюр поперечных сил и изгибающих моментов.

1. Эпюра Q является прямолинейной на всех участках. На тех участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси эпюры, а эпюра М, в общем случае, – наклонными прямыми (рис. 6.13).

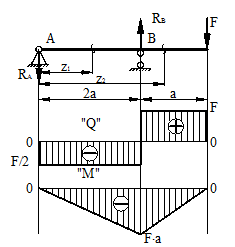
Рис.6.13

2. На тех участках, где к балке приложена равномерно распределенная нагрузка, эпюра Q ограничена наклонными прямыми, а эпюра М – квадратичными параболами (рис. 6.14). При построении эпюры М на сжатых волокнах, выпуклость параболы обращена в сторону, противоположную действию распределенной нагрузки (рис. 6.15,а, б).

Рис.6.14

3. В тех сечениях, где Q = 0, касательная к эпюре М параллельна оси эпюры (рис. 6.14, 6.15). Изгибающий момент в таких сечениях балки экстремален по величине (М_max, M_min).

4. На участках, где Q>0, M возрастает, то есть слева на право положительные ординаты эпюры M монотонно увеличиваются, отрицательные – монотонно уменьшаются (рис. 6.13, 6.14); на тех участках, где Q < 0, M убывает (рис. 6.13, 6.14).

5. В тех сечениях, где к балке приложены сосредоточенные силы:

а) на эпюре Q будут скачки на величину и в направлении приложенных сил (рис. 6.13, 6.14).

б) на эпюре M будут переломы (рис. 6.13, 6.14), острие перелома направлено против действия силы.

6. В тех, сечениях, где к балке приложены сосредоточенные моменты, на эпюре M будут скачки на величину этих моментов, на эпюре Q никаких изменений не будет (рис. 6.16).

Рис.6.15

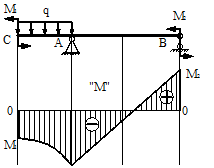
Рис.6.16

7. Если на конце консоли или в концевой опоре приложен сосредоточенный момент, то в этом сечении изгибающий момент равен внешнему моменту (сечения C и B на рис. 6.16).

8. Эпюра Q представляет собой диаграмму производной от эпюры M. Значит, ординаты Q пропорциональны тангенсу угла наклона касательной к эпюре M (рис. 6.14).

9. Порядок линии на эпюре Q всегда на единицу меньше, чем на эпюре M. Например, если эпюра M - квадратная парабола, то эпюра Q на этом участке - наклонная прямая; если эпюра M - наклонная прямая, то эпюра Q на этом участке - прямая, параллельная оси; если M =const (прямая, параллельная оси), то на этом участке Q=0.

10. Приращение функции изгибающего момента на рассматриваемом участке численно равно площади эпюры поперечных сил на этом участке с соответствующим знаком. При построении эпюры для изгибающего момента слева направо знаки приращения функции изгибающего момента и площади эпюры поперечных сил совпадают. При построении эпюры изгибающих моментов справа налево знаки приращения функции изгибающих моментов и площади эпюры поперечных сил противоположны. Покажем это.

На рис. 6.16.1 изображены эпюры поперечной силы (рис. 6.16.1,а) и изгибающих моментов (рис. 6.16.1,б). Воспользуемся дифференциальной зависимостью для определения изгибающего момента в сечении В, если значение изгибающего момента в сечении А известно. Проинтегрируем выражение в пределах длины участка l:

Рис

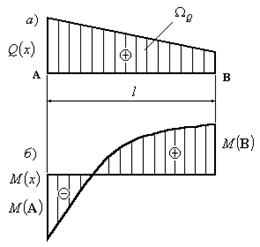
Рис. 6.16.1

Здесь Ω_Q - по определению для определенного интеграла есть площадь эпюры поперечных сил Q(x) на участке длиной l.

Таким образом, изгибающий момент в сечении В может быть найден из выражения

M(B)=M(A)+∆M.

Знак приращения функции изгибающего момента в данном случае положительный, так как эпюра изгибающих моментов строилась слева направо и знак площади эпюры поперечных сил на всем рассматриваемом участке положительный.

Воспользуемся изложенными следствиями из дифференциальных зависимостей для контроля качества правильности построения эпюр поперечных сил и изгибающих моментов. Рассмотрим несколько примеров.

Пример 1.

Какая из эпюр поперечных сил, изображенных на рис. 6.16.2, построена правильно?

Анализируя эпюры для поперечной силы, приведенные на рис.6.16.2, приходим к выводу, что верной оказывается эпюра, приведенная под номером 2. При анализе правильности построения эпюры для поперечной силы следует использовать следствия из дифференциальных зависимостей, изложенные выше.

Начинать анализ следует либо с определения опорных реакций и проставления их на схеме балки, либо с выбора возможных направлений опорных реакций без предварительного определения их величин. Затем следует задать себе вопрос: возможен ли в сечении А скачок на величину реакции R_A?

Рис

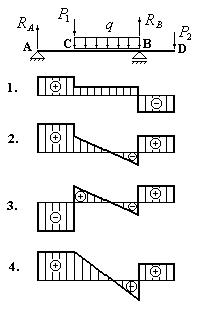
Рис. 6.16.2

Да, скачок возможен в направлении реакции R_A на ее величину. Этому случаю соответствуют эпюры, изображенные под №1, №2, и №4. Таким образом, для дальнейшего рассмотрения следует исключить вариант №3. Далее следует обратить внимание на наличие распределнной нагрузки на первом участке. Распределенная нагрузка на первом участке отсутствует, следовательно, на основании следствия №1 из дифференциальных зависимостей поперечная сила на первом участке балки должна быть постоянной. Этому условию соответствуют все три из оставшихся вариантов. В сечении С к балке приложена сосредоточенная сила P₁. На основании первого следствия о скачках в этом сечении должен быть скачок на величину силы P₁ в направлении ее действия. Этому случаю из оставшихся вариантов соответствуют варианты №1 и №2. Таким образом, вариант №4 отпадает. Далее исследуем поведение эпюры для поперечной силы на втором участке. На этом участке действует распределенная нагрузка интенсивности q. На основании второго следствия из дифференциальных зависимостей на участке, где действует распределенная нагрузка, поперечная сила должна меняться по линейному закону. Этому случаю соответствует из оставшихся двух вариантов только вариант №2. Таким образом, из четырех возможных вариантов нами выбран вариант эпюры для поперечной силы под № 2. Проследим дальнейшее поведение эпюры поперечной силы для варианта №2. В сечении В действует опорная реакция R_B. Поэтому на эпюре поперечных сил должен наблюдаться скачок на величину этой реакции в направлении ее действия. Такой скачок действительно наблюдается. На третьем участке балки отсутствует распределенная нагрузка. Следовательно, поперечная сила на этом участке должна быть постоянной, что и наблюдается на эпюре для поперечных сил под номером 2. И, наконец, в сечении D на эпюре для поперечной силы должен быть скачок на величину силы P₂, которая действует в этом сечении, в направлении действия этой силы. Действительно, такой скачок на эпюре поперечной силы в сечении D наблюдается.

Рассмотрим пример анализа правильности построения эпюры для изгибающих моментов с использованием следствий из дифференциальных зависимостей.

Пример 2.

Какая из эпюр изгибающих моментов, изображенных на рис.6.16.3, построена правильно?

Рис

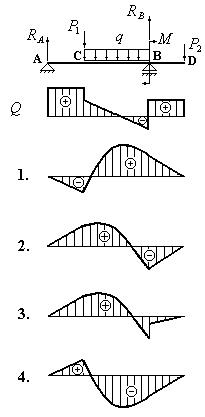
Рис. 6.16.3

На рис. 6.16.3 варианты эпюр изгибающих моментов обозначены цифрами 1, 2, 3, 4. Какой из этих вариантов правильный? Анализ начнем с определения величины изгибающего момента в сечении А. В этом сечении изгибающий момент должен быть равен нулю. Такой результат соответствует всем вариантам. На первом участке отсутствует распределенная нагрузка и в соответствии с первым следствием из дифференциальных зависимостей изгибающий момент должен на этом участке изменяться по линейной зависимости. Действительно, для всех четырех вариантов это следствие выполняется. Однако, в соответствии с пятым следствием из дифференциальных зависимостей на первом участке должен наблюдаться подъем на эпюре изгибающих моментов, так как поперечная сила на этом участке положительна. Напомним, что в соответствии с пятым следствием приращение функции изгибающего момента на участке численно равно площади эпюры поперечной силы. Знак приращения функции изгибающего момента совпадает со знаком площади эпюры поперечных сил при построении эпюры слева направо. Таким образом, с учетом этого следствия вариант эпюры для изгибающего момента под номером 1 выпадает, так как на первом участке на эпюре изгибающего момента наблюдается не подъем, а спуск. В сечении С на эрюре поперечной силы наблюдается скачок, поэтому на эпюре изгибающих моментов в этом сечении должен наблюдаться излом. Для эпюр изгибающих моментов с номерами 2 и 3 этот излом незначительный, для варианта №4 этот излом оказывается довольно большим. На втором участке действует распределенная нагрузка постоянной интенсивности. В соответствии со вторым следствием из дифференциальных зависимостей на этом участке эпюра изгибающих моментов должна меняться по закону квадратной параболы. Действительно, для всех оставшихся вариантов изгибающий момент на втором участке меняется по закону квадратной параболы, но в соответствии с четвертым следствием из дифференциальных зависимостей на этом участке выпуклость на эпюре изгибающих моментов должна быть обращена навстречу интенсивности распределенной нагрузки. Это явление мы наблюдаем на эпюрах под номерами 2 и 3. На эпюре изгибающих моментов под номером 4 выпуклость обращена в ту же сторону, что и интенсивность распределенной нагрузки. Поэтому вариант эпюры изгибающих моментов под номером 4 неверен. Таким образом, остаются варианты под номерами 2 и 3. Какой из этих вариантов верен? Обратимся к сечению С. В этом сечении действует сосредоточенная пара сил с моментом M. В соответствии со вторым следствием о скачках в этом сечении должен наблюдаться скачок на эпюре изгибающих моментов на величину внешнего момента. На эпюре с номером 3 такой скачок есть. На эпюре изгибающих моментов с номером 2 скачок отсутствует. На основании изложенного делаем вывод, что вариант эпюры изгибающих моментов с номером 2 неверен. Правильным оказался вариант с номером 3. Проследим, как ведет себя эпюра для изгибающего момента на третьем участке балки. Поперечная сила на этом участке положительна, а это означает, что на эпюре изгибающих моментов на этом участке должен наблюдаться подъем, что мы и видим на эпюре под номером 3.

В приведенных примерах проиллюстрирована возможность анализа правильности построения эпюр поперечных сил и изгибающих моментов. Использование следствий о скачках и следствий из дифференциальных зависимостей между интенсивность распределенной нагрузки, поперечной силой и изгибающим моментом позволяет строить “качественные” (без расчета) эпюры M и Q. В некоторых случаях быстрое “качественное” построение эпюр поперечных сил и изгибающих моментов позволяет инженеру экономить время и дает возможность прочуствовать конструкцию, выделить опасные сечения и принять соответствующее решение.

Примеры построения эпюр внутренних силовых факторов для консольных балок

При построении эпюр Q_y и M_x в консольных, или жестко защемленных, балках нет необходимости вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

Пример 3.

Рассмотрим балку длиной l защемленную одним концом и находящуюся под действием сосредоточенной силы Р (рис.6.17). Пусть для определенности Р=4 кН, l = 2 м.

Рис.6.17

Решение.

Определим внутренние силовые факторы, возникающие в балке. Воспользуемся методом сечением.

Рассечем балку поперечным сечением в произвольном месте.

Отбросим правую часть.

Заменим ее действие внутренними усилиями N - вдоль оси z, Q_y - вдоль оси y и моментом M_x – в плоскости осей yz вокруг оси х. На рис.6.17 в соответствии с принятым правилом знаков показаны положительные направления внутренних силовых факторов.

Уравновесим отсеченную часть. Запишем уравнения статического равновесия, получим

Из первого уравнения видно, что нормальная сила N при изгибе равна нулю, далее не будем ее определять.

Построим эпюры поперечной силы Q_y и изгибающего момента M_x вдоль длины балки.

Поперечная сила постоянна по всей длине балки и равна Q_y = P = 4 кН. Отложим на графике линию параллельную оси z.

Изгибающий момент М_х изменяется в зависимости от расстояния z. Вычислим его значение в двух точках: в начале z = 0 и в конце балки z = l = 2 м.

z = 0 (М_х = 0);

z = 2 м (М_х = 8 кНм).

Построим по точкам график М_х.

Построение эпюр поперечной силы Q_y и изгибающего момента M_x является одним из основных этапов при расчете конструкций на изгиб. По эпюрам Q_y и M_x определяется опасное сечение, т.е. сечение в котором может произойти разрушение.

Опасным сечением называется сечение, в котором изгибающий момент достигает наибольшего по модулю значения M_xmax=max|M_x|.

В некоторых случаях опасным сечением может быть также сечение, где наибольшего значения достигает поперечная сила Q_ymax=max|Q_y|. В данном случае опасным является место закрепления балки где М_х = 8 кНм.

Пример 4.

Построить эпюры поперечных сил и изгибающих моментов для изображенной на рис. 6.17.1,а балки.

Рис

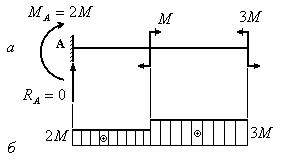
Рис. 6.17.1

Решение.

1. Из условия равновесия определяем опорные реакции: R_A=0; M_A=2M.

2. Поперечная сила на всем протяжении длины балки равна нулю: Q_y=0.

3. Изгибающий момент на первом участке M_x=M_A=2M. На втором участке изгибающий момент найдем справа: M_x=3M. Изгибающий момент на каждом из участков от продольной координаты не зависит. Следовательно, изгибающий момент на каждом из участков балки будет величиной постоянной.

Эпюра изгибающих моментов изображена на рис. 6.17.1,б.

Пример 5.

Построить эпюры Q_y и M_x (рис.6.18). Дано: M=50 кНм; q=10 кН/м.

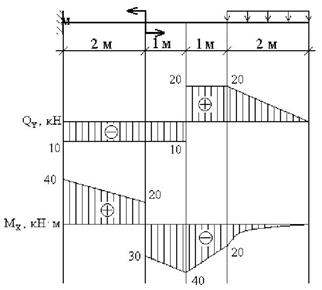
Рис. 6.18

Решение.

1. Намечаем характерные сечения.

2. Определяем поперечную силу Q_y в каждом характерном сечении.

По вычисленным значениям строим эпюру Q_y.

3. Определяем изгибающий момент M_x в каждом характерном сечении.

По вычисленным значениям строим эпюру M_x, причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.

Пример 6.

Построить эпюры Q_y и M_x для консольной балки (рис.6.19).

В данном случае для правильного построения эпюры M_x необходимо использовать приведенные выше дифференциальные зависимости.

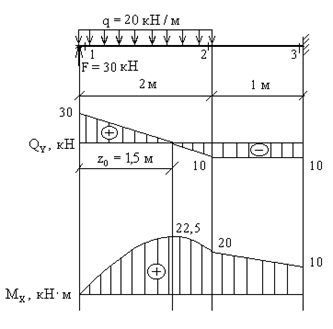
Рис. 6.19

Решение.

1. Намечаем характерные сечения.

2. Определяем поперечные силы в характерных сечениях.

3. Строим эпюру Q_y.

Характер эпюры, то есть тот факт, что эпюра Q_y пересекает ось, говорит о том, что в этом сечении момент M_x будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении Q_y=dM_x/dz=0, а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.

Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры Q_y разделить на интенсивность распределенной нагрузки q:

Определяем изгибающие моменты в характерных сечениях.

4. Вычисляем экстремальное значение изгибающего момента в сечении, где :

Строим эпюру M_x.

Примеры построения эпюр внутренних силовых факторов для балок на двух опорах

В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.

Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия ΣF_ix=0 обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:

Условие ΣF_iy=0 используется для проверки вычисленных значений опорных реакций.

Рассмотрим примеры построения эпюр Q_y и M_x.

Пример 7.

z₁

Построить эпюры поперечных сил и изгибающих моментов для изображенной на рис.6.20,а балки.

Рис

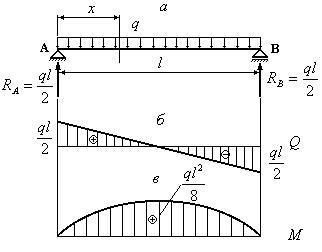
Рис. 6.20

Решение.

1. Из условия равновесия определяем опорные реакции:

2. Рассекаем балку в произвольном сечении и составляем уравнение для поперечной силы:

Выражение (a) представляет собой закон изменения поперечной силы по длине балки, из которого следует, что поперечная сила является линейной функцией продольной координаты x.

Эпюра для поперечной силы представлена на рис. 6.20,б.

3. Составляем уравнение для изгибающего момента:

Из выражения (б) следует, что изгибающий момент является квадратичной функцией продольной координаты x.

При x=0 изгибающий момент M_x =0;

при x=l изгибающий момент M_x =0.

Эпюра изгибающих моментов представлена на рис. 6.20,в.

Анализируя построенные эпюры, приходим к выводу, что опасным является сечение посредине балки, в котором действует наибольший по абсолютной величине изгибающий момент

Пример 8.

z₁

Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 6.20.1,а.

Рис

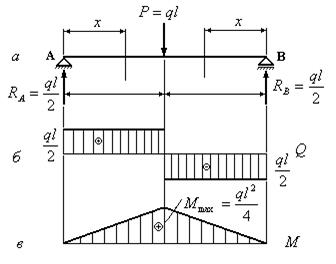
Рис. 6.20.1

Решение.

1. Из условия равновесия определяем опорные реакции:

2. Разобьем балку на участки.

3. Рассечем балку на первом участке сечением x и запишем уравнение для поперечной силы:

Из уравнения (a) следует, что поперечная сила от продольной координаты x не зависит и является постоянной на первом участке балки.

4. Уравнение для изгибающих моментов на первом участке запишем в виде:

Из уравнения (б) следует, что изгибающий момент на первом участке балки является линейной функцией продольной координаты x.

При x=0 изгибающий момент M_x =0;

5. Для построения эпюр Q_y и M_x на втором участке поместим начало координат в точку В. Поперечная сила на втором участке будет равна:

Из уравнения (в) следует, что поперечная сила от продольной координаты x не зависит и является постоянной на первом участке балки.

Уравнение для изгибающих моментов на втором участке принимает вид:

Из уравнения (г) следует, что изгибающий момент на втором участке балки является линейной функцией продольной координаты x.

При x=0 изгибающий момент M_x =0;

Эпюры для поперечной силы и для изгибающего момента изображены на рис.6.20.1,б и 6.20.1,в.

Пример 9.

z₁

Для балки, изображенной на рис.6.20.2 построить эпюры поперечной силы Q_y и изгибающего момента M_x и определить опасное сечение. Пусть величины P = 10 кН, a = 2 м, b = 3 м.

Рис. 6.20.2

Решение.

Определим реакции опор. Запишем уравнения равновесия статики. Из этих уравнений получим:

Для проверки правильности определения реакции опор используем уравнение:

6 – 10 + 4 = 0,

0=0.

Значит, реакции определены правильно.

Определим внутренние усилия, возникающие в материале балки. Следует рассмотреть два участка, границами участков являются точки приложения сосредоточенной силы Р и опорных реакций R_A и R_B. Обозначим границы участков буквами А, С и В.

Рассечем первый участок АС.

Отбросим правую часть, т.к. она сложнее.

Заменим отброшенную часть внутренними усилиями Q_y и M_x.

Уравновесим отсеченную часть, запишем уравнения равновесия:

Вычислим Q_y и M_xв граничных точках участка:

при z₁ = 0, Q_y₁ = R_A = 6 кН, M_x₁ = 0;

при z₁ = а = 2 м, Q_y₁ = R_A = 6 кН, M_x₁ = 12 кНм.

Рассмотрим второй участок СВ. Рассечем его и отбросим левую часть, заменим её внутренними силами. Из уравнений равновесия получим

Вычислим Q_y и M_xв граничных точках участка:

при z₂ = 0, Q_y₂ = - R_В = - 4 кН, M_x₂ = 0;

при z₂ = а = 3 м, Q_y₂ = - R_В = - 4 кН, M_x₂ = 12 кНм.

Построим эпюры Q_y и M_x (рис.6.20.2).

По полученным эпюрам определим опасное сечение, оно проходит через точку приложения силы P, так как M_x достигает там наибольшего значения.

Пример 10.

Для представленной на рис.6.21 балки построить эпюры внутренних сил, найти опасные сечения.

Рис.6.21

Решение.

Определим реакции опор. Заменим распределенную нагрузку q её равнодействующей G=2qa, приложим G в середине участка АС (рис.6.22).

Запишем уравнение равновесия.

Рис.6.22

Отсюда находим:

Выполним проверку правильности определения реакций опор.

0=0.

Используя метод сечений, рассмотрим сечения участков балки (рис.6.23).

Рис.6.23

1 участок:

Вычислим Q_y₁ и M_x₂ на границах участка.

2 участок:

На границах участка получим

Построим эпюры Q_y и M_x на участках. Из выражений для внутренних усилий следует, что Q_y, эпюра является прямолинейной как на первом, так и на втором участках, в то время как эпюра М_х на первом участке квадратичная парабола, а на втором прямая линия. Для построения эпюры М_х на первом участке следует либо вычислить её значения в нескольких точках, либо исследовать функцию на экстремум и определить его.

Как известно из курса математического анализа, для определения экстремума функции следует определить ее первую производную, приравняв ее нулю найти аргумент, затем его значение подставить в функцию и вычислить экстремум функции.

Отложим значение М_х_max и построим эпюру изгибающего момента на первом участке по трем точкам (рис.6.23). По эпюре находим опасное сечение. Им является сечение, где .

Пример 11.

Построить эпюры Q_y и M_x для балки с шарнирным опиранием (рис.6.24).

Рис. 6.24

Решение.

1. Вычисляем реакции опор.

Проверка:

2. Намечаем характерные сечения.

В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.

3. Определяем поперечные силы в характерных сечениях.

Строим эпюру Q_y.

4. Определяем изгибающие моменты в характерных сечениях.

Строим эпюру M_x

Пример 12.

Построить эпюры Q_y и M_x для балки на двух опорах с консолью (рис.6.25,а).

Решение.

1. Вычисляем опорные реакции.

Во втором уравнении равновесия (впрочем, как и в первом) момент от распределенной нагрузки q вычислен без разбиения ее на две части - слева и справа от опоры В, то есть определена равнодействующая нагрузки q - q∙3, ее положение (в середине участка с распределенной нагрузкой), что позволяет определить плечо равнодействующей относительно опоры В и направление создаваемого ею момента. В то же время можно было в уравнении равновесия учитывать отдельно части нагрузки q, приложенные слева и справа от опоры В; при этом второе уравнение равновесия имеет вид:

Рис.6.25

Вычисленное из этого уравнения значение реакции R_A, разумеется, совпадает с полученным ранее.

Проверка:

2. Намечаем характерные сечения.

3. Вычисляем поперечную силу и изгибающий момент в характерных сечениях.

Из рассмотрения левой отсеченной части:

Для сечений 5-7 удобнее рассматривать правую отсеченную часть:

По вычисленным значениям строим эпюры Q_y и M_x (рис.6.25, б,в).

Пример 13.

Написать выражения для поперечной силы Q_y и изгибающего момента M_x в сечении x для балки, изображенной на рис.6.25.1.

Рис

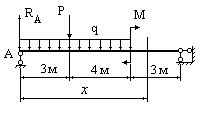
Рис. 6.25.1

Решение.

1. Уравнение для поперечной силы имеет вид:

2. Уравнение для изгибающего момента принимает вид:

Другие подходы к построению эпюр внутренних силовых факторов

Помимо описанного выше, можно выделить еще один подход к построению эпюр. В этом случае намечают характерные сечения, в качестве которых выделяют точки приложения сосредоточенных сил и моментов, а также точки начала и конца участков с распределенными нагрузками. Затем определяют величину внутреннего силового фактора слева и справа (бесконечно близко) от характерной точки.

Этот метод существенно отличается от аналитического метода, так как в результате его применения нельзя получить уравнения распределения внутренних силовых факторов в пределах рассматриваемого участка изгибаемого элемента конструкции. С помощью этого метода можно получить лишь численные значения поперечной силы и изгибающего момента в том или ином сечении.

Однако такой подход в сочетании с использованием следствий из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом позволяет быстро и качественно строить эпюры различной сложности.

Рассмотрим применения этого метода на примере.

Пример 14.

Построить эпюры поперечных сил Q и изгибающих моментов M для изображенной на рис.6.25.2,а балки по методу “характерных” сечений.

Рис

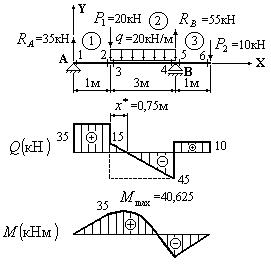
Рис. 6.25.2

Решение.

1. Определяем опорные реакции. Для этого составим два уравнения равновесия:

Из уравнения (а) находим величину реакции R_B:

Из уравнения (б) находим величину реакции R_A:

Выполняем проверку. Для этого составим уравнение проекций всех сил, действующих на балку, на вертикальную ось Oy:

2. Разбиваем балку на участки и проставляем “характерные” сечения 1- 6 на границах участков.

3. Определяем величины для поперечной силы в каждом из “характерных” сечений:

Откладываем от базисной линии найденные значения для поперечной силы в каждом из “характерных” сечений и соединяем полученные точки, руководствуясь следствиями из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом.

На участке №1 распределенная нагрузка отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей поперечная сила будет постоянной. Соединяем точки, соответствующие значениям поперечной силы, найденным в сечениях №1 и №2, горизонтальной прямой. На втором участке действует распределенная нагрузка постоянной интенсивности. Следовательно, на основании следствия №2 из дифференциальных зависимостей поперечная сила должна меняться по линейному закону. Поэтому соединяем точки соответствующие значениям поперечной силы, найденным в сечениях №3 и №4 наклонной прямой. На участке №3 распределенная нагрузка так же, как и на участке №1, отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей поперечная сила будет постоянной. Соединяем точки, соответствующие значениям поперечной силы, найденным в сечениях №5 и №6 горизонтальной прямой.

При построении эпюры поперечных сил следует обращать внимание на возможные скачки в тех сечениях, в которых приложены сосредоточенные силы. Так, в сечениях №2 и №3 значения для поперечной силы отличаются на величину силы P₁=20 кН. В сечениях №4 и №5 значения для поперечной силы отличаются на величину реакции R_B=55 кН. В сечении №6 также наблюдается скачок на величину силы P₂=10 кН в направлении ее действия при построении эпюры слева направо.

4. Находим значения для изгибающих моментов в “характерных” сечениях:

Откладываем от базисной линии найденные значения для изгибающих моментов в “характерных” сечениях и соединяем полученные точки, руководствуясь следствиями из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом.

На участке №1 распределенная нагрузка отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей изгибающий момент будет меняться по линейному закону. Соединяем точки, соответствующие значениям изгибающих моментов, найденным в сечениях №1 и №2, наклонной прямой. На втором участке действует распределенная нагрузка постоянной интенсивности. Следовательно, на основании следствия №2 из дифференциальных зависимостей изгибающий момент должен меняться по закону квадратной параболы. При этом на основании следствия №4 выпуклость на эпюре изгибающих моментов должна быть обращена навстречу распределенной нагрузке, т.е. вверх. Соединяем точки, соответствующие значениям изгибающих моментов, найденным в сечениях №3 и №4 параболой, обращенной выпуклостью вверх. На участке №3 распределенная нагрузка так же, как и на участке №1, отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей изгибающий момент будет меняться по линейному закону. Поэтому соединяем точки, соответствующие значениям изгибающих моментов, найденных в сечениях №5 и №6 наклонной прямой. Скачков на эпюре изгибающих моментов не наблюдается, так как отсутствуют сосредоточенные моменты, приложенные к балке. Следует обратить внимание, что в сечениях, в которых имеются скачки на эпюре поперечных сил, на эпюре изгибающих моментов должны быть изломы.

Найдем величину максимального изгибающего момента M_max. На втором участке балки поперечная сила меняет знак, пересекая базисную линию. Сечение, в котором поперечная сила равна нулю, также считается “характерным”. В этом сечении изгибающий момент достигает экстремальной величины на рассматриваемом участке. Для рассматриваемой балки изгибающий момент будет максимальным на основании дифференциальной зависимости так как интенсивность распределенной нагрузки q<0.

Для определения максимального изгибающего момента сначала определим координату сечения, в котором момент максимален. Для этого на эпюре поперечных сил сформируем два треугольника (контур одного из треугольников показан пунктиром). Один из рассматриваемых треугольников имеет неизвестный катет длиной x*, который и следует определить. Выделенные треугольники подобны по трем углам. Составим пропорцию: решая которую относительно x*, получим

Максимальный изгибающий момент можно определить двумя способами:

1. Помещая начало координат в точке А балки на левом ее конце, вычислим координату сечения, в котором изгибающий момент достигает максимальной величины: x_max=x*+1=1,75 м, составляем выражение для изгибающего момента в указанном сечении и подставляем в это выражение координату x_max=1,75 м. Получим:

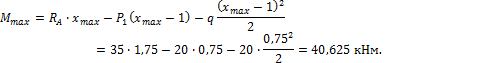
2. Используя следствие №10 из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом, максимальный изгибающий момент найдем, прибавив к значению изгибающего момента в сечении №3 площадь эпюры поперечной силы Q на участке длиной x*=0,75 м:

Последний способ определения изгибающих моментов в некоторых случаях может оказаться предпочтительнее, так как существенно экономит время.

Приведенные примеры построения эпюр поперечных сил и изгибающих моментов для балок и эпюр поперечных сил, изгибающих моментов и продольных усилий для рам позволяют получить наглядное представление о преимуществах и недостатках метода “характерных” сечений. К числу преимуществ этого метода можно отнести простоту определения внутренних силовых факторов. К числу недостатков – отсутствие аналитических законов распределения внутренних силовых факторов по длине элементов конструкции. Однако, использования дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом для анализа поведения распределения внутренних усилий и следствий из них в значительной мере компенсирует последний недостаток. Сделанный вывод позволяет рекомендовать метод построения эпюр распределения внутренних силовых факторов по “характерным’ сечениям в учебную практику.

Напряжение при чистом изгибе

Рассмотрим наиболее простой случай изгиба, называемый чистым изгибом и выведем формулу для определения нормальных напряжений для данного случая. Отметим, что методами теории упругости можно получить точную зависимость для нормальных напряжений при чистом изгибе, если же решать эту задачу методами сопротивления материалов, необходимо ввести некоторые гипотезы.

Таких гипотез при изгибе три:

1) гипотеза плоских сечений (гипотеза Бернулли). Сечения плоские до деформации остаются плоскими и после деформации, а лишь поворачиваются относительно некоторой линии, которая называется нейтральной осью сечения балки. При этом волокна балки, лежащие с одной стороны от нейтральной оси будут растягиваться, а с другой - сжиматься; волокна, лежащие на нейтральной оси своей длины не изменяют;

2) гипотеза о постоянстве нормальных напряжений - напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса;

3) гипотеза об отсутствии боковых давлений - соседние продольные волокна не давят друг на друга.

Кроме этих гипотез следует ввести ряд ограничений:

1. Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости.

2. Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков.

3. Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.

Приведенные выше гипотезы в обычных случаях изгиба верны только приблизительно. Однако вытекающие из них погрешности теории так невелики, что ими можно пренебречь.

Как было отмечено выше, под чистым изгибом понимается такой вид сопротивления, при котором в поперечных сечениях бруса возникают только изгибающие моменты, а поперечные силы равны нулю. Для тех участков бруса, где соблюдается данное условие, изгибающий момент, вдоль продольной оси z принимает постоянное значение. Так как в любом сечении стержня при чистом изгибе M_x(z)=const, то для однородного бруса постоянного поперечного сечения изменение кривизны постоянно вдоль оси z. Под действием изгибающих моментов ось бруса искривляется. Исходя из этого, ось бруса принимает форму дуги окружности с радиусом кривизны (рис. 6.26). В данном случае с высокой степенью точности справедлива гипотеза плоских сечений. Следовательно, точки, расположенные до изгиба в плоскости поперечного сечения бруса, в результате изгиба переместятся в пространстве таким образом, что их совокупность снова образует плоскость.

Процесс формирования деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сечений друг относительно друга.

Рассмотрим два смежных сечения, отстоящих один от другого на расстоянии dz (рис. 6.26).

В результате изгиба эти сечения наклонятся, образуя между собой угол dθ, в связи с чем верхние волокна удлиняются, а нижние - укоротятся. Очевидно, что при этом существует слой, длина которого не изменилась. Назовем его нейтральным слоем и обозначим отрезком СD. При этом . Произвольный отрезок АВ, расположенный от СD на расстоянии y, в результате изгиба удлинится на величину . С учетом построений, изображенных на рис. 6.26, легко определить величину его относительной линейной деформации:

Рис.6.26

Если предположить, что продольные волокна не давят друг на друга, то каждое из них будет находиться в условиях простого растяжения - сжатия. Тогда переход от деформаций к нормальным напряжениям можно осуществить посредством закона Гука:

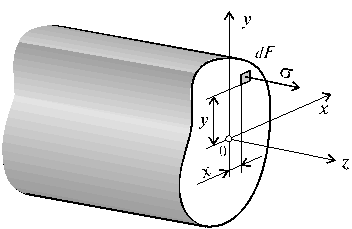
Рис. 6.27

Установим положение нейтральной оси x, от которой происходит отсчет координаты у (рис.6.27). Учитывая, что сумма элементарных сил по площади поперечного сечения A дает нормальную силу N_z. Но при чистом изгибе N_z =0, следовательно:

Как известно, последний интеграл представляет собой статический момент сечения относительно нейтральной линии (оси x). Статический момент равен нулю, значит, нейтральная линия проходит через центр тяжести сечения.

Выразим момент внутренних сил относительно нейтральной оси M_xчерез σ. Очевидно, что

C учетом выражения (2) получим:

Откуда

где - кривизна нейтрального волокна; EI_x - жесткость бруса.

Из формулы (3), исключая , окончательно получим:

Эта формула была впервые получена Ш. Кулоном в 1773 году.

Таким образом, нормальные напряжения в любой точке сечения прямо пропорциональны величине изгибающего момента и расстоянию точки от нейтральной линии сечения и обратно пропорционально моменту инерции сечения относительно нейтральной оси.

Из выражения (5) можно сделать ряд важных выводов:

1) центр тяжести сечения балки является началом координат для анализа напряжений и приведения внешних сил;

2) напряжения изгиба зависят от значений изгибающего момента, момента инерции сечения и координаты точки, в которой это напряжение определяется;

3) напряжения в любой точке, лежащей на одинаковом расстоянии от нейтральной линии, равны между собой;

4) нормальные напряжения не зависят, а упругие перемещения зависят от модуля упругости материала балки.

В нейтральном слое при y=0 напряжения σ=0, в сжатой зоне (при y<0, рис.6.26) напряжения становятся отрицательными, в растянутой зоне (при y>0, рис. 6.26) напряжения становятся положительными. По мере удаления от нейтрального слоя нормальные напряжения σ в поперечном сечении бруса при его изгибе изменяются по линейному закону в зависимости от координаты y и принимают максимальное значение на уровне крайних волокон (при ):

Измеряется осевой момент сопротивления единицами длины в третьей степени, например (см³). Физический смысл момента сопротивления состоит в следующем: чем больше W_x, тем больший изгибающий момент может принять на себя балка, не подвергаясь опасности разрушения. Таким образом, величина момента сопротивления характеризует влияние формы и размеров поперечного сечения балки на ее способность сопротивляться внешним нагрузкам, не разрушаясь.

При симметричном относительно нейтральной линии сечении, например, прямоугольном, расстояния до крайних растянутых и сжатых волокон одинаковы и такое сечение имеет одно вполне определенное значение момента сопротивления относительно оси Oz. Так, при высоте прямоугольника (рис. 6.27.1, а), равной h

Рис

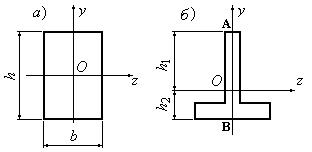
Рис. 6.27.1

Если сечение несимметрично относительно нейтральной линии – тавр, мы получим два момента сопротивления: один для волокон А (рис. 6.27.1,б): и другой для волокон В: . Теперь в формулу (6) следует вводить: W₁ - при вычислении напряжений в точке А и W₂ - при вычислении напряжений в точке В.

Для круга

Для прокатных профилей (двутавра, швеллера, уголка) M_xприводится в таблицах сортамента.

Формулой (6) удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня получает вид

где maxM_x — максимальное значение изгибающего момента (легко определяемое по его эпюре), [σ] - допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором σ=const).

При расчете балок из хрупких материалов следует различать наибольшие растягивающие maxσ_p и наибольшие сжимающие maxσ_c напряжения, которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение [σ_p] и сжатие [σ_c]. Условие прочности в этом случае будет иметь вид:

В зависимости от того, чему лучше сопротивляется материал, приходится соответсвующим образом конструировать сечение, выбирая его форму и размеры так, чтобы удовлетворяли условию прочности.

Из условия (7) формулируют три рода задач на прочность при изгибе:

1. Проверка прочности: задана балка, нагрузка, известен материал. Строится эпюра M_x – определяется M_max, вычисляется W_x и по (7) проверяется условие прочности.

2. Определение максимально допустимой нагрузки по условию прочности.

Заданы размеры балки, характер нагрузки, материал балки.

Строится эпюра M_x – определяется M_max от параметра нагрузки, вычисляется W_x и по (8) находят наибольший параметр нагрузки.

3. Конструирование балки – определение размеров ее поперечного сечения.

Строится эпюра – определяется , вычисляется правая часть (9) и подбираются размеры поперечного сечения, удовлетворяющие (9).

Для прямоугольного сечения

Обычно задаются отношением

Тогда

отсюда

Задаваясь шириной b по (10) получим h.

Для двутаврового сечения по таблице сортамента подбирают номер двутавра с W_x большим, чем правая часть (9).

Рассмотрим примеры определения нормального напряжения в произвольной точке сечения изгибаемой балки.

Пример 15.

Определить нормальное напряжение при изгибе балки (в МПа) в точке А поперечного сечения, удаленной от нейтральной линии сечения на 15 см (рис. 6.27.2), если изгибающий момент M=10 кНм.

Рис

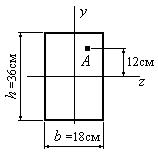
Рис. 6.27.2

Решение.

1. Определяем момент инерции сечения относительно оси z:

2. Подставляем значения изгибающего момента, осевого момента инерции и координаты точки А в формулу для нормальных напряжений (5) и находим напряжения:

Таким образом, в точке А поперечного сечения балки действует нормальное напряжение σ_A=1,745 МПа.

Рассмотрим несколько примеров определения моментов сопротивления сечений и расчета балок на прочность.

Пример 16.

У которой из фигур (рис. 6.27.3), имеющих одинаковую площадь, момент сопротивления относительно оси z, будет наибольшим? Определить наибольший момент сопротивления.

Рис

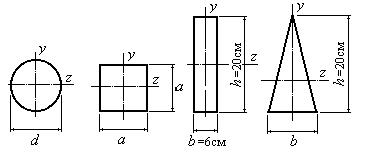
Рис. 6.27.3

Решение.

Ранее в примере 14 в разделе 4 «Геометрические характеристики плоских сечений» были найдены моменты инерции каждого из сечений относительно центральной оси сечения z.

Найдем моменты сопротивления:

для сечения круглой формы:

для сечения квадратной формы:

для сечения прямоугольной формы:

для сечения треугольной формы:

Таким образом, наибольший момент сопротивления оказался у сечения прямоугольной формы: W_z=400 см³.

Пример 17.

На рисунке изображены поперечные сечения 4-х балок (рис. 6.27.4), изготовленных из одинакового материала. Которая из балок является наиболее прочной?

Рис

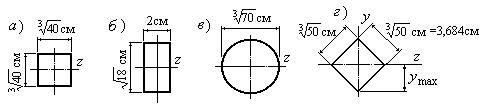
Рис. 6.27.4

Решение.

Наиболее прочной будет балка, у которой момент сопротивления относительно оси z будет наибольший. Вычислим моменты сопротивления W_z для каждого из сечений.

а) Квадратное сечение.

б) Прямоугольное сечение.

в) Круглое сечение.

г) Ромбовидное сечение. Рассматриваемое сечение получилось путем поворота горизонтальной оси квадратного сечения на 45°. В результате момент инерции сечения относительно оси z не изменился и может быть вычислен как для квадратного сечения:

Осевой момент сопротивления найдем, разделив момент инерции на y_max:

Таким образом, наибольший момент сопротивления оказался у круглого поперечного сечения: W_z=6,87 см³. Следовательно, балка с круглым поперечным сечением обладает наибольшей прочностью.

Пример 18.

Как изменится прочность балки, если поперечное сечение будет переведено из положения “I” в положение “II” (рис. 6.27.5)?

Рис

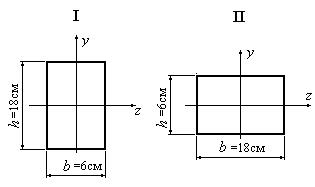
Рис. 6.27.5

Решение.

1. Вычислим осевой момент сопротивления W_z для положения сечения I:

2. Вычислим осевой момент сопротивления W_z для положения сечения II:

3. Найдем отношение осевых моментов инерции для положения сечения I и II:

Таким образом, при переводе сечения из положения I в положение II прочность балки уменьшается в 3 раза.

Энергия упругих деформаций балки

Энергия упругих деформаций балки при изгибе V определяется работой момента M_x на соответствующем угловом перемещении dθ:

окончательно получим

Касательные напряжения при поперечном изгибе. Главные напряжения при изгибе

В случае поперечного изгиба в сечениях балки возникают не только изгибающий момент, но и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения.

Так как касательные напряжения в общем случае распределены по сечению неравномерно, то при поперечном изгибе поперечные сечения балки, строго говоря, не остаются плоскими. Однако при h/l<<1 (где h - высота поперечного сечения, l - длина балки) оказывается, что эти искажения заметным образом не сказываются на работе балки на изгиб. В данном случае гипотеза плоских сечений и в случае чистого изгиба с достаточной точностью приемлема. Поэтому для расчета нормальных напряжений σ применяют ту же формулу (5).

Рассмотрим вывод расчетных формул для касательных напряжений. Выделим из бруса, испытывающего поперечный изгиб, элемент длиной dz (рис. 6.28,а).

Рис. 6.28

Продольным горизонтальным сечением, проведенным на расстоянии y от нейтральной оси, разделим элемент на две части (рис. 6.28,в) и рассмотрим равновесие верхней части, имеющей основание шириной b. При этом с учетом закона парности касательных напряжений, получим, что касательные напряжения в поперечном сечении равны касательным напряжениям, возникающим в продольных сечениях (рис. 6.28,б). С учетом данного обстоятельства и из допущения о том, что касательные напряжения по площади bdz распределены равномерно, используя условие Σz=0получим:

откуда

где - равнодействующая нормальных сил в левом поперечном сечении элемента dz в пределах заштрихованной площади :

С учетом (5) последнее выражение можно представить в виде

где - статический момент части поперечного сечения, расположенной выше координаты y (на рис. 6.28,б эта область заштрихована). Следовательно, (15) можно переписать в виде

откуда

В результате совместного рассмотрения (13) и (16) получим

поэтому окончательно

Полученная формула (17) носит имя русского ученого Д.И. Журавского.

Дмитрий Иванович Журавский – русский механик и инженер – принимал участие в постройке Николаевской железной дороги из Петербурга в Москву, спроектировал и построил металлический шпиль Петропавловского собора в Петербурге. Его работы посвящены применению математических методов в строительной механике. Он впервые дал определение касательных напряжений в изгибаемых балках и вывел формулу для определения касательных напряжений при изгибе.

Условие прочности по касательным напряжениям:

где - максимальное значение поперечной силы в сечении; - допускаемое касательное напряжение, оно, как правило, равно половине .

Для исследования напряженного состояния в произвольной точке балки, испытывающей поперечный изгиб, выделим из состава балки вокруг исследуемой точки элементарную призму (рис. 6.28,г), таким образом, чтобы вертикальная площадка являлась частью поперечного сечения балки, а наклонная площадка составляла произвольный угол α относительно горизонта. Принимаем, что выделенный элемент имеет следующие размеры по координатным осям: по продольно оси - dz, т.е. по оси z; по вертикальной оси - dy, т.е. по оси у; по оси х - равный ширине балки.

Так как вертикальная площадка выделенного элемента принадлежит поперечному сечению балки, испытывающему поперечный изгиб, то нормальные напряжения σ на этой площадке определяются по формуле (5), а касательные напряжения τ - по формуле Д.И. Журавского (17). С учетом закона парности касательных напряжений, легко установить, что касательные напряжения на горизонтальной площадке также равны τ. Нормальные же напряжения на этой площадке равны нулю, согласно уже известной нам гипотезе теории изгиба о том, что продольные слои не оказывают давления друг на друга.

Обозначим величины нормальных и касательных напряжений на наклонной площадке через и , соответственно. Принимая площадь наклонной площадки dF, для вертикальной и горизонтальной площадок будем иметь dFsinα и dFcosα, соответственно.

Составляя уравнения равновесия для элементарной вырезанной призмы (рис. 6.28,г), получим:

откуда будем иметь:

Следовательно, окончательные выражения напряжений на наклонной площадке принимают вид:

Определим ориентацию площадки, т.е. значение α=α₀, при котором напряжение σ_α принимает экстремальное значение. Согласно правилу определения экстремумов функций из математического анализа, возьмем производную функции σ_α от α и приравняем ее нулю:

Предполагая α=α₀, получим:

Откуда окончательно будем иметь:

Согласно последнему выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называемых главными, а сами напряжения - главными напряжениями.

Сопоставляя выражения и , имеем:

откуда и следует, что касательные напряжения на главных площадках всегда равны нулю.

В заключение, с учетом известных тригонометрических тождеств:

и формулы

определим главные напряжения, выражая из через σ и τ:

Полученное выражение имеет важное значение в теории прочности изгибаемых элементов, позволяющее производить расчеты их прочности, с учетом сложного напряженного состояния, присущее поперечному изгибу.

Пример 19.

В качестве примера применения формулы Журавского построим эпюру касательных напряжений для случая прямоугольного поперечного сечения балки (рис. 6.29). Учитывая, что для этого сечения

получаем

где F=bh - площадь прямоугольника.

Как видно из формулы, касательные напряжения по высоте сечения меняются по закону квадратической параболы, достигая максимума на нейтральной оси

Рис. 6.29

В круглом сечении (рис. 6.29) эпюра касательных напряжений ограничена кривой, имеющей максимум на нейтральной оси. Учитывая, что статический момент полукруга и момент инерции круга

получаем

Следовательно, максимальные касательные напряжения в круглом сечении на 33% больше средних напряжений , по которым, например, обычно проводится расчет заклепок.

Для треугольного сечения с основанием b и высотой h (рис. 6.29), имеем

Максимальное напряжение имеет место на расстоянии y=h/6 от нейтральной линии, то есть в точках средней линии треугольника.

При изгибе тонкостенных профилей касательные напряжения определяются по следующей формуле:

где δ - толщина тонкостенного профиля.

На рис. 6.30 построена эпюра τ при изгибе тонкостенного двутавра в вертикальной плоскости симметрии. Вследствие симметрии сечения и нагрузки, касательные напряжения в симметричных точках полок двутавра должны быть также симметричны относительно оси y и будут увеличиваться от края к центру по линейному закону:

Вдоль стенки τ изменяются по параболическому закону

и направлены в ту же сторону, что и сила Q.

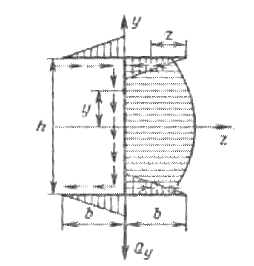
Рис. 6.30

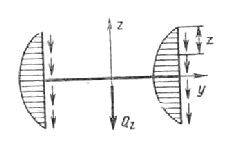
Рис. 6.31

При изгибе двутавра в плоскости второй оси (рис. 6.31) касательные напряжения в стенке равны нулю, а вдоль каждой из полок изменяются по параболическому закону

Пример 20.

Построить эпюру распределения касательных напряжений для балки двутаврового (№ 12) сечения (рис. 6.32), если Q=10 кН.

Рис. 6.32

Решение.

Для построения эпюры схематизируем действительное сечение, представив его в виде трех прямоугольников, как показано на рис. 6.32 пунктиром. Проведя произвольную линию mn, параллельную нулевой линии, и перемещая ее вдоль оси y, обнаруживаем, что при этом напряжения в точках этой линии меняются по параболическому закону, так как мы имеем дело с прямоугольниками. Для построения эпюры касательных напряжений вычислим τ в крайних волокнах (линия AB), в месте сопряжения полки со стенкой (точки 1 и 2, причем будем считать, что они расположены бесконечно близко к границам полки, но лежат по разные стороны от этой границы) и в точках нейтральной линии.

На рис. 6.32 все размеры даны в мм, а напряжения – в МПа.

Для точек линии AB ширина сечения равна l, а статический момент равен нулю, так как линия AB не отсекает никакой площади. Таким в точках линии AB касательные напряжения равны нулю.

Для точки 1 статический момент равен

Момент инерции сечения относительно нейтральной оси находим по сортаменту I_z=403 см⁴. Касательное напряжение в точке 1:

Для точки 2 статический момент (с точностью до бесконечно малых величин) остается таким же, но ширина сечения d=0,5 см. Поэтому касательное напряжение в точке 2

Для точек

Следовательно, при переходе от точки 1 к точке 2 касательное напряжение возрастает в 15 раз и на эпюре получается скачок.

Для точек нейтральной линии ширина сечения d=0,5 см, а статический момент следует взять для половины сечения из сортамента S_z^max=38,5 см³. Поэтому

На основании этих данных строим эпюру касательных напряжений для нижней половины сечения. Для верхней половины сечения в силу симметрии профиля относительно оси z эпюра будет симметричной.

Построенная эпюра условна, так как она дает верные значения касательных напряжений только для точек стенки, достаточно удаленных от полок. Вблизи полок касательные напряжения в стенке возрастают, ввиду того, что место сопряжения полки со стенкой является источником концентрации касательных напряжений. В полках же, где отношение высоты к ширине много меньше единицы, возникают касательные напряжения, перпендикулярные направлению Q, и величина их меняется по ширине сечения.

Необходимо отметить также, что формулой Журавского можно пользоваться только в случае прямого изгиба.

Пример 21.

Определить касательные напряжения в указанных точках двутаврового сечения и построить эпюру касательных напряжений при величине поперечной силы Q=50 кН (рис. 6.32.1).

Рис

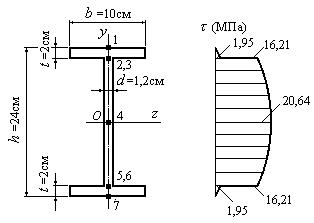
Рис. 6.32.1

Решение.

Характерной особенностью этого сечения является резкое изменение ширины сечения при переходе от стенки двутавра к его полке. В основном поперечную силу воспринимает стенка, а на долю полок приходится небольшая ее величина.

Покажем, как определяется статический момент площади для любой произвольной точки сечения двутавра. Для этого рассмотрим произвольную точку К (рис. 6.32.2). Проведем через эту точку линию, параллельную оси Oz. Статический момент площади верхней отсеченной части (заштрихованой на рис. 6.32.2) может быть найден как сумма статических моментов двух площадей A₁ и A₂

Рис

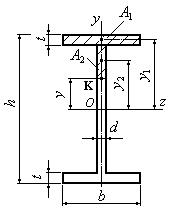
Рис. 6.32.2

Наибольшей величины статический момент площади отсеченной части относительно нейтральной линии сечения Oz достигает для половины сечения. Следовательно, максимальные касательные напряжения возникают в волокнах нейтрального слоя.

Вернемся теперь к рис.6.32.1. Точка №1 сечения принадлежит наиболее отдаленному волокну. Точки №2 и №3 лежат в месте перехода от полки к стенке: точка №2 принадлежит полке, точка №3 – стенке сечения. Точка №4 лежит в центре тяжести сечения и принадлежит нейтральной линии сечения. Сечение симметрично расположено по отношению к оси Oz. Поэтому напряжение в точке №5 будет таким же, как в точке №3, напряжение в точке №6 – таким же, что и в точке №2, напряжение в точке №7 – таким же, что и в точке №1.

Вначале найдем момент инерции сечения относительно оси Oz:

Касательное напряжение в точке №1 поперечного сечения равно нулю, так как отсеченная часть сечения в данном случае представляет собой пространство над сечением, и ввиду отсутствия отсеченной площади, статический момент этой площади равен нулю. С другой стороны, если в качестве отсеченной площади рассматривать все сечение, то статический момент всей площади относительно нейтральной линии сечения , как центральной оси, равен нулю.

Для определения касательного напряжения в точке №2 проводим через точку №2 линию, параллельную оси Oz. Отсеченная площадь лежит выше этой линии и составляет =2∙10=20см². Вычисляем расстояние от центра тяжести отсеченной площади до оси Oz. Оно равно 11см. Находим касательные напряжения в точке №2:

При определении касательного напряжения в точке №3 следует помнить, что статический момент площади отсеченной части в этом случае остается прежним, так как точки №2 и №3 находятся на одинаковом расстоянии от оси Oz. Только точка №2 принадлежит полке, а точка №3 принадлежит стенке двутавра. В связи с этим касательное напряжение в точке №3 будет равно:

Для определения напряжения в точке №4, проведем через эту точку линию, совпадающую с осью Oz. Отсеченная площадь представляет собой тавр. Статический момент площади тавра вычислим, используя выражение (а), приведенное выше. В нем A₁ представляет собой площадь полки, A₂ - площадь половины стенки; y₁ - расстояние от центра тяжести полки до оси Oz; y₂ - расстояние от центра тяжести половины площади стенки до оси Oz. Касательные напряжения в точке №4 будут равны:

Как уже отмечалось выше, в силу симметрии τ₅=τ₃=16,21 МПа, τ₆=τ₂=1,95 МПа; τ₇=τ₁=0.

Откладываем найденные значения касательных напряжений от базисной линии и строим эпюру касательных напряжений (рис. 6.32.1).

Пример 22.

Во сколько раз касательное напряжение в точке В больше, чем в точке А? Точка О – центр тяжести сечения (рис. 6.32.3).

Рис

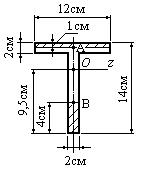
Рис. 6.32.3

Решение.

Проведем через точки А и В линии, параллельные оси Oz. Отсеченные площади на рис. 6.32.3 заштрихованы. Вычислим статические моменты заштрихованных площадей относительно оси Oz и отнесем их к ширине сечения в точках А и В соответственно.

При одной и той же поперечной силе и одном и том же моменте инерции сечения относительно оси Oz касательные напряжения в точках В и А относятся как:

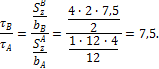
Таким образом, касательное напряжение в точке В в 7,5 раз больше, чем в точке А.

Пример 23.

Как изменится максимальное касательное напряжение при изгибе, если поперечное сечение балки перевести из положения I в положение II ? (рис. 6.32.4).

Рис

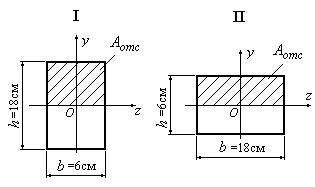
Рис. 6.32.4

Решение.

При решении данной задачи следует помнить, что при повороте сечения из положения I в положение II меняются не только ширина сечения и статический момент площади сечения (отсеченные площади заштрихованы), но и моменты инерции относительно оси Oz. Поэтому при одной и той же поперечной силе величины максимальных касательных напряжений в положених сечения I и II будут относиться, как:

Таким образом, величина максимального касательного напряжения при повороте сечения из положения I в положение II не изменится.

Пример 24.

Какая из изображенных эпюр касательных напряжений при изгибе построена правильно? (рис. 6.32.5).

Рис

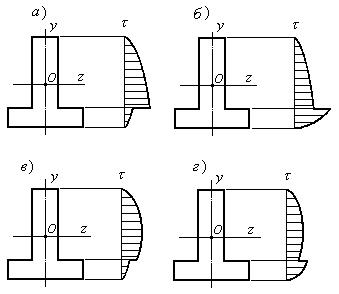
Рис. 6.32.5

Решение.

При анализе таких эпюр следует помнить:

1. Максимальные касательные напряжения возникают в нейтральном слое. Нейтральная линия сечения проходит через центр тяжести.

2. В месте резкого изменения ширины сечения касательные напряжения меняются скачком. При увеличении ширины сечения напряжения скачкообразно уменьшаются, при уменьшении ширины сечения касательные напряжения скачкообразно увеличиваются. Поэтому из предложенных вариантов эпюр касательных напряжений верным является вариант в).

Пример 25.

Для балки из пластичного материала, передающей в опасном сечении изгибающий момент M_max=32 кНм, подобрать двутавровое и прямоугольное сечение (h/b=2), если [σ]=160 МПа. Сравнить массы подобранных балок.

Момент сопротивления определяется из условия прочности:

Ближайший стандартный двутавровый профиль подбираем по сортаменту:

Для прямоугольного сечения имеем:

Отношение масс подобранных профилей равно отношению площадей поперечных сечений и составляет 3:1, то есть балка прямоугольного сечения более чем в три раза тяжелее балки двутаврового сечения при условии равной их прочности.

Сделаем несколько замечаний, касающихся расчетов на прочность при прямом поперечном изгибе. В отличие от простых видов деформации, когда в поперечных сечениях стержня возникает лишь один силовой фактор, к которым относятся и изученные выше растяжение (сжатие) и чистый изгиб, прямой поперечный изгиб должен быть отнесен к сложным видам деформации. В поперечных сечениях стержня при поперечном изгибе возникают два силовых фактора: изгибающий момент M_x и поперечная сила Q_y (рис.6.33), напряженное состояние является упрощенным плоским, при котором в окрестности произвольно выбранных точек поперечного сечения действуют нормальные σ и касательные τ напряжения. Поэтому условие прочности для таких точек должно быть сформулировано на основе какого-либо уже известного критерия прочности.

Однако учитывая, что наибольшие нормальные напряжения возникают в крайних волокнах, где касательные напряжения отсутствуют (рис.6.33), а наибольшие касательные напряжения во многих случаях имеют место в нейтральном слое, где нормальные напряжения равны нулю, условия прочности в этих случаях формулируются раздельно по нормальным и касательным напряжениям

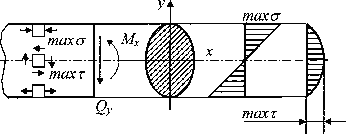
image041-11
Рис.6.33. Распределение нормальных и касательных напряжений

по контуру сечения

Покажем, что доминирующая роль в расчетах на прочность балки, подвергнутой поперечному изгибу, будет принадлежать расчету по нормальным напряжениям. Для этого оценим порядок σ_max и τ_max на примере шарнирно опертой балки, показанной на рис. 6.34. На рис.6.34 показаны эпюры поперечных сил и изгибающих моментов соответственно.

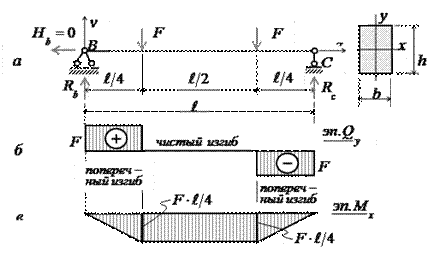
Рис.6.34

В нашем случае максимальные нормальные напряжения будут равны

максимальные касательные напряжения будут равны

а их отношение дает нам

Отсюда σ_max>>τ_max. Таким образом, для достаточно больших отношений l/h≥10 (длинные балки), касательные напряжения существенно меньше нормальных напряжений. Указанная порядковая оценка, за небольшими возможными исключениями, сохраняется вообще для всех нетонкостенных балок.

По этой причине расчет на прочность длинных балок при поперечном изгибе обычно производится только по нормальным напряжениям, например, для балки из пластичного материала, работающей на прямой изгиб, как и в случае чистого изгиба будет иметь вид:

Рациональные формы поперечных сечений при изгибе

Наиболее рациональным следует признать сечение, обладающее минимальной площадью при заданной нагрузке (изгибающем моменте) на балку. В этом случае расход материала на изготовление балки, будет минимальным.

Изгибающий момент, который сечение способно выдержать безопасно, пропорционален моменту сопротивления W_z. Величина наибольшего действующего в сечении напряжения σ_max должна быть ограничена значением [σ], и тогда допускаемый момент

Расход же материала пропорционален площади сечения A. Следовательно, чем больше отношение , тем больший изгибающий момент выдерживает сечение с заданной площадью и тем меньше материала уйдет на изготовление стержня. Поэтому отношение может быть принято за критерий, оценивающий качество профиля:

Чем больше будет этот показатель, тем рациональнее будет сечение. Основываясь на этом критерии (или просто обратив внимание на то, какая часть материала расположена вблизи нейтральной линии), можно убедиться, что трубчатое сечение, показанное на рис. 6.35,а рациональнее сплошного круглого, а расположение прямоугольника, показанное на рис.6.35,б, при вертикальной силовой плоскости выгоднее, чем показанное на рис.6.35,в.

Рис

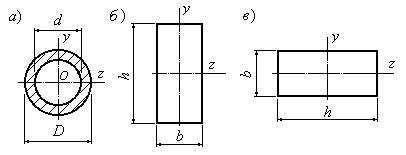
Рис. 6.35

Для получения балки минимальной материалоемкости нужно стремиться к тому, чтобы по возможности наибольший объем материала работал при напряжениях, равных допускаемым или близким к ним. Заметим также, что если условие прочности выполняется и максимальное напряжение близко к допускаемому, то это не означает еще, что сечение подобрано удачно, так как при другой форме сечения и значительно меньшем σ_max балка может быть намного легче.

Прежде всего рациональное сечение балки при изгибе должно удовлетворять условию равнопрочности растянутой и сжатой зон балки. Иными словами необходимо, чтобы наибольшие напряжения растяжения () и наибольшие напряжения сжатия () одновременно достигали допускаемых напряжений и .

Поэтому для балки из пластичного материала (одинаково работающего на растяжение и сжатие: , условие равнопрочности выполняется для сечений, симметричных относительно нейтральной оси. К таким сечениям относится, например, прямоугольное сечение (рис.6.35.1,а), при котором обеспечено условие равенства . Однако в этом случае материал, равномерно распределенный по высоте сечения, плохо используется в зоне нейтральной оси. Чтобы получить более рациональное сечение, необходимо возможно большую часть материала переместить в зоны, максимально удаленные от нейтральной оси. Таким образом, приходим к рациональному для пластичного материала сечению в форме симметричного двутавра (рис.6.35.1,б), у которого возможно большая часть материала сосредоточена на полках (горизонтальных массивных листах), соединенных стенкой (вертикальным листом), толщина которой δ назначается из условий прочности стенки по касательным напряжениям, а также из соображений ее устойчивости. К двутаврому сечению близко по критерию рациональности так называемое коробчатое сечение (рис. 6.35.1, в).

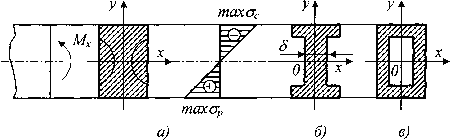
image059-7
Рис.6.35.1. Распределение нормальных напряжений в симметричных сечениях

Рассуждая аналогично, приходим к выводу, что для балок из хрупкого материала наиболее рациональным будет сечение в форме несимметричного двутавра, удовлетворяющего условию равнопрочности на растяжение и сжатие (рис. 6.36):

которое вытекает из требования

Рис.6.36. Распределение напряжений несимметричного

профиля сечения балки.

image063-6
Рис.6.37. Используемые профили сечений:

а) двутавр, б) швеллер, в) неравнобокий уголок, г) равнобокий уголок

Идея рациональности поперечного сечения стержней при изгибе реализована в стандартных тонкостенных профилях, получаемых методами горячего прессования или прокатки из рядовых и легированных конструкционных высококачественных сталей, а также алюминия и алюминиевых сплавов, получивших широкое распространение в строительстве, машиностроении, авиационном машиностроении. Широко распространены показанные на рис.6.37: а—двутавр, б— швеллер, в — неравнобокий уголок, г—равнобокий уголок. Реже встречаются тавр, таврошвеллер, зетовый профиль и др. Употребляются также холодногнутые замкнутые сварные профили (рис.6.38).

Рис.6.38. Замкнутые сварные профили

Поскольку по соображениям технологии сортамент стандартных профилей по размерам ограничен (например, наибольший прокатный двутавр согласно ГОСТ 8239—72 имеет высоту 550 мм), то для больших пролетов приходится применять составные (сварные или клепаные) балки.

Пример 26.

Какое из представленных на рисунке поперечных сечений (рис.6.38.1) является более рациональным в соответствии с критерием рациональности при плоском поперечном изгибе?

Рис

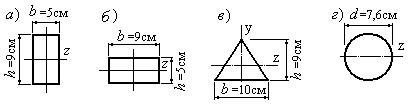
Рис. 6.38.1

Решение.

Найдем для каждого из сечений осевые моменты сопротивления, площадь и из выражения значение критерия рациолнальности:

1. Прямоугольное сечение (рис.6.38.1, а):

2. Прямоугольное сечение (рис.6.38.1, б):

3. Треугольное сечение (рис.6.38.1, в):

4. Круглое сечение (рис.6.38.1, г):

Сравнивая полученные значения для критерия рациональности k, можно сделать вывод, что при практически одинаковых площадях всех сечений, представленных на рис.6.38.1, наиболее рациональным оказалось сечение с наибольшим моментом сопротивления (вертикально расположенное сечение (рис.6.38.1, а) с W_z=67,5 см³). Критерий рациональности у этого сечения составил k=1,5.

Полная проверка прочности. Опасные сечения и опасные точки

Для проверки на прочность при изгибе по действующим на балку внешним нагрузкам строят эпюры изменения внутренних усилий по ее длине и определяют опасные сечения балки, для каждого из которых необходимо провести проверку прочности.

При полной проверке прочности таких сечений будет, как минимум, три (иногда они совпадают):

1. сечение, в котором изгибающий момент М_х - достигает своего максимального по модулю значения, - именно по этому сечению подбирают сечение всей балки;

2. сечение, в котором поперечная сила Q_y, достигает своего максимального по модулю значения;

3. сечение, в котором и изгибающий момент М_x и поперечная сила Q_y достигают по модулю достаточно больших величин.

В каждом из опасных сечений необходимо, построив эпюры нормальных и касательных напряжений, найти опасные точки сечения (проверка прочности проводится для каждой из них), которых также будет, как минимум, три:

1. точка, в которой нормальные напряжения σ_z, достигают своего максимального значения, - то есть точка на наружной поверхности балки наиболее удаленная от нейтральной оси сечения;

2. точка, в которой касательные напряжения τ достигают своего максимального значения, - точка, лежащая на нейтральной оси сечения;

3. точка, в которой и нормальные напряжения, и касательные напряжения, достигают достаточно больших величин (эта проверка имеет смысл для сечений типа тавра или двутавра, где ширина резко изменяет свое значение).

Пример 27.

Для заданных двух схем балок (рис.6.39) требуется написать выражения Q_y, M_x для каждого участка в общем виде, построить эпюры Q_y, M_x, найти M_xmax и подобрать: для схемы а) деревянную балку круглого поперечного сечения при [σ]=8 МПа; для схемы б) стальную балку двутаврового поперечного сечения при [σ]=160 МПа. При М = 20 кН/м, Р = 20 кН, q = 8 кН/м, l₁=12 м, l₂=8 м, a₁/a=2, a₂/a=8, a₃/a=3.

а) б)

Рис.6.39

Решение.

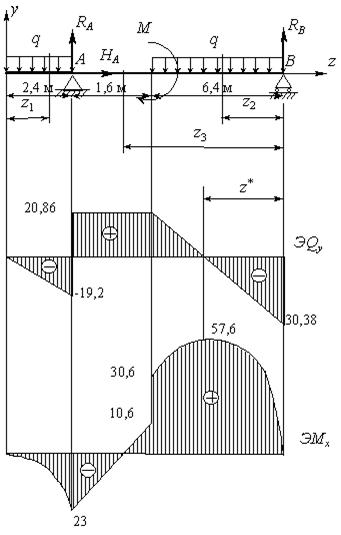
а) б)

Рис. 6.40

Схема а).

1. Для определения внутренних усилий Q_y, M_x используем метод сечений. Определим количество участков: граничными точками участков являются точки приложения сосредоточенных сил и моментов, а также точки начала и конца распределенной нагрузки. В данной задаче консольная балка имеет два участка. Рассечем последовательно со свободного конца каждый из них. Отбрасывая часть балки, включавшую защемление, определим внутренние силовые факторы в сечении. Поперечная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на поперечную ось (ось у), изгибаюший момент равен алгебраической сумме моментов, возникающих на отсеченной части относительно оси х в сечении. При определении знаков, используем следующее правило: поперечная сила положительна, если отсеченная часть стремится повернуться по часовой стрелке относительно, точки сечения, изгибающий момент положителен, если балка становится вогнутой.

Запишем выражения для внутренних силовых факторов и сосчитаем их значения в граничных точках участков (рис.6.40,а).

1 участок: м

II участок: м

2. Построим эпюры внутренних силовых факторов, откладывая вычисленные значения на графике (рис.6.40,а). Соединим полученные точки прямыми линиями на участках, где аргумент z входит в первой степени и параболами, где z входит во второй степени. Таким образом, эпюра изгибающего момента на первом участке будет криволинейной, остальные участки эпюр будут прямолинейными. Определим опасное сечение балки, т.е. сечение, в котором изгибающий момент достигает наибольшего по модулю значения. Опасным сечением будет сечение на опоре, где M_x₁(1,2)=-10,33 кНм.

3. Диаметр круглого сечения найдем из условия прочности

Схема б).

1. Для балки, лежащей на двух шарнирных опорах (рис.6.40,б), найдем опорные реакции R_А, Н_А, R_В . Запишем уравнения равновесия статики:

Для проверки правильности определения реакций запишем еще одно уравнение равновесия, которое должно тождественно удовлетвориться при правильно найденных значениях реакций.

Балка имеет три участка, рассечем каждый из них.

I участок:

II участок: м

2. Построим эпюры, соединяя полученные значения Q_y и M_x. На втором участке эпюра M_x имеет максимум при . Для определения величины максимального момента приравняем нулю выражение поперечной силы на участке, определим величину и подставим ее в выражение изгибающего момента:

Двутавровое сечение найдем из условия прочности, определив необходимую величину момента сопротивления

Из сортамента прокатной стали (ГОСТ 8239-72) выберем двутавр с см³,

Перемещения при изгибе балок. Дифференциальное уравнение изогнутой оси упругой балки

При расчете балок на изгиб инженер интересуется не только напряжениями, возникающими от действия внешних сил, но и перемещениями от действия тех же сил. Одно из требований к элементам конструкций, чтобы перемещение не превосходило некоторого допустимого значения, обусловленного требованиями эксплуатации. Это условие называется условием жесткости либо конструктивной прочности.

Если балка при нагружении сильно прогибается, то при эксплуатации сооружения, имеющего гибкие балки, появятся затруднения и, кроме того, могут возникнуть колебания балки с большими амплитудами, а вместе с тем и значительные дополнительные напряжения.

Под жесткостью следует понимать способность элеменов конструкций и деталей машин сопротивляться внешним нагрузкам без видимых деформаций. Расчет на жесткость заключается в оценке упругой податливости балки под действием приложенных нагрузок и подбор таких размеров поперечного сечения, при которых перемещения не будут превышать установленных нормами пределов. Для выполнения такого расчета необходимо научиться вычислять перемещения сечений балки под действием любой внешней нагрузки.

При расчете строительных и машиностроительных конструкций на жесткость (в большинстве случаев по прогибам, по углам поворота) должно соблюдаться условие

т.е. относительный прогиб f/l, подсчитанный при действии нормативных нагрузок, не должен превышать установленный нормами предельный прогиб 1/n_o для данного вида конструкции. Число n₀ устанавливается нормами проектирования примерно в пределах от 300 до 1000. Для ответственных сооружений, например, для железнодорожных мостов, величина n₀ принимается равной 1000. Отсюда видно, что прогибы при изгибе, как правило, малы по сравнению с пролетом балки.

Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости – ограничение угла поворота φ опорных сечений:

Допускаемый угол поворота φ_adm берется из соответствующих справочников. В среднем φ_admсоставляет 0,001 рад.

Рассмотрим плоский чистый изгиб балки (рис. 6.41, а).

Ось балки (рис. 6.41,а) под действием нагрузки, расположенной в одной из главных плоскостей инерции (в плоскости yOz), искривляется в той же плоскости, а поперечные сечения поворачиваются и одновременно получают поступательные перемещения. Искривленная ось балки называется изогнутой осью или упругой линией.

а) б)

Рис. 6.41

В результате действия изгибающего момента m ось балки ОС изгибается и занимает некоторое положение ОС'. Произвольная точка А оси балки, характеризуемая координатой z, перемещается в новое положение А'. Перемещение, изображаемое направленным отрезком , назовем прогибом балки для точки А с координатой z и обозначим v. Наибольший прогиб СС' =v_max=f называется стрелой прогиба.

Проведем в точке А' касательную к изогнутой оси балки. Она образует с осью z угол . Из рис. 6.41,б видно, что этот угол в силу взаимной перпендикулярности сторон в точности равен углу поворота поперечного сечения. При изменении z, т.е. при переходе к другим точкам оси балки, прогиб v и угол поворота θ поперечного сечения изменяется. Следовательно, они являются функциями z:

Горизонтальное перемещение w произвольной точки D поперечного сечения на расстоянии y от оси балки равно:

Из треугольника А'В'В" следует, что первая производная от функции прогиба v(z):

равна тангенсу угла наклона касательной к изогнутой оси балки в точке А с координатой z. Из этого же треугольника получаем

Из рис. 6.41,б находим , где ρ - радиус кривизны дуги . Следовательно, кривизна изогнутой оси в точке А равна:

Дифференцируя (21) по z и учитывая (19), (22), (23), получаем:

откуда

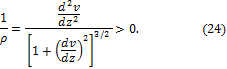
Формула для кривизны балки

для положительных значений M_x. В нашем примере на рис. 6.41 изгибающий момент . Поэтому эту формулу мы должны использовать в виде:

Приравнивая (24), (25), получаем точное дифференциальное уравнение изогнутой оси балки:

Если прогибы v балки малы по сравнению с ее линейными размерами, то и углы поворота сечений θ - малые величины и, согласно (21)-(24), можно считать:

Тогда дифференциальное уравнение (26) упрощается и принимает вид

Уравнение (27) носит название приближенного дифференциального уравнения изогнутой оси упругой балки. Оно получено для случая чистого изгиба, но может быть использовано и при поперечном, когда момент является функцией z.

Интегрируя (27), получаем:

Произвольные постоянные C₁, С₂ в (28) имеют простой геометрический смысл. Обозначим через прогиб и угол поворота cечения соответственно в начале координат при z=0. Тогда при z=0 из (10) получаем:

Величины называют начальными параметрами задачи по определению перемещений в балках.

Соотношения (28) запишем в виде

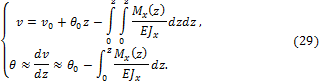
Так как

то решение (29) можно записать в виде:

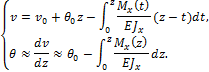
В соответствии с дифференциальными зависимостями Журавского

Дифференцируя (27) дважды по z и используя зависимости (30), находим

При постоянной жесткости получаем

Уравнения (32), (34) представляют собой вторую форму дифференциальных уравнений изогнутой оси балки четвертого порядка.

Общее решение неоднородного уравнения (34) имеет вид

где - его частное решение. Постоянные находятся из условий на опорах балки. Эти условия называют граничными или краевыми.

Рассмотрим типичные условия закрепления или опирания балок (рис. 6.42). Изогнутая ось балки изображена тонкой линией.

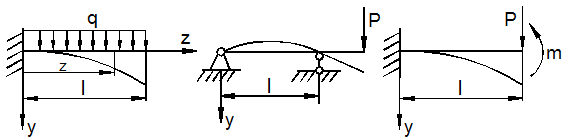
а) б) в)

Рис. 6.42

а) Край балки жестко защемлен (рис. 6.42,а). При z = 0 на защемленном крае прогиб и угол поворота сечения равны нулю, т.е.

б) Край балки свободен от закрепления и нагрузки (рис.6.42,а). В этом случае при z=l равны нулю: момент и перерезывающая сила:

в) Край балки шарнирно закреплен либо свободно опёрт (рис. 6.42,б). При z = 0 край балки шарнирно закреплен. Здесь прогиб v и момент M_xравны нулю, т.е.

При z=l балка свободно лежит на опоре. Прогиб равен нулю, но изгибающий момент в сечении балки отличен от нуля. Поэтому здесь только одно граничное условие v=0.

г) Незакрепленный край балки с действующими сосредоточенными силой и моментом (рис. 6.42,в).

В этом случае при z=l имеем статические граничные условия:

Рассмотрим несколько примеров применения метода непосредственного интегрирования приближенного уравнения упругой линии балки.

Пример 28.

Определить стрелу прогиба и угол поворота сечения В балки, изображенной на рис. 6.42.1.

Рис

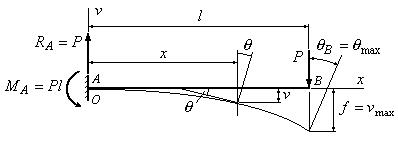
Рис. 6.42.1

Решение.

1. Из условий равновесия определяем опорные реакции:

2. Выбираем начало координат O на левом конце балки, совмещая его с точкой А. Ось Ov направляем вверх, ось Ox - вправо.

3. Составляем уравнение изгибающего момента в сечении x:

4. Предполагая, что жесткость балки постоянна, записываем приближенное дифференциальное уравнение упругой линии балки:

Знак “+” в уравнении упругой лиинии был принят потому, что ось Ov направлена вверх.

5. Интегрируем уравнение первый раз. Получаем:

Интегрируя еще раз, получаем уравнение для прогиба в сечении x:

Так как в заделке прогиб и угол поворота равны нулю, то для определения постоянных интегрирования граничные условия имеют вид:

при x=0 θ(x)=0;

при x=0 v(x)=0.

Из уравнения (а) видно, что постоянная C представляет собой угол поворота в начале координат (сечении А). Задавая в уравнении (а) x=0, находим C=0. Из уравнения (б) следует, что постоянная D - прогиб в начале координат. Задавая в уравнении (б) x=0, получаем D=0.

Таким образом, получаем следующие выражения для прогиба и угла поворота:

Подставляя в первое уравнение x=l, найдем стрелу прогиба:

Подставляя во второе уравнение x=l, найдем максимальный угол поворота

Знак “-” у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси Oy. Знак “-” в выражении угла поворота показывает, что сечение В повернулось не против, а по часовой стрелке.

Пример 29.

Определить стрелу прогиба двухопорной балки и углы поворота опорных сечений А и В (рис.6.42.2).

Рис

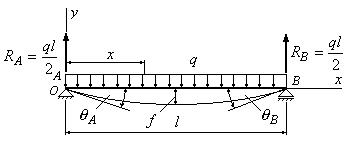
Рис. 6.42.2

Решение.

1. Из условий равновесия определяем опорные реакции:

3. Составляем уравнение изгибающего момента в сечении x:

Знак “+” в уравнении упругой лиинии был принят потому, что ось Ov направлена вверх.

5. Интегрируем уравнение первый раз. Получим:

Интегрируя еще раз, получаем уравнение для прогиба в сечении x:

Постоянные интегрирования найдем из граничных условий:

при x=0 v=0;

при x=l v=0.

Подставляя в уравнение (г) x=0 и приравнивая прогиб нулю, получим D=0; подставляя в это же уравнение x=l, находим постоянную интегрирования C:

Найденные значения постоянных интегрирования подставим в уравнения (в) и (г) и получим уравнения углов поворота и прогибов:

Подставляя x=0 и x=l в первое уравнение, получим углы поворота соответственно сечений А и В:

В силу симметрии нагрузки максимальный прогиб будет посредине балки. Подставляя во второе уравнение x=l/2, получим:

Как и в предыдущем примере, знак “-” у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси Ov. Знак “-” в выражении угла поворота θ_A показывает, что сечение А повернулось не против, а по часовой стрелке, знак “+” в выражении угла поворота θ_B показывает, что сечение В повернулось против часовой стрелки.

Пример 30.

В сколько раз прогиб в сечении В на конце изображенной на рис. 6.42.3 балки, больше, чем прогиб в сечении С посредине балки?

Рис

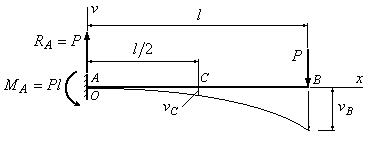
Рис. 6.42.3

Решение.

Воспользуемся результатами, полученными в примере 28. Запишем окончательное выражение для прогиба:

и подставим в это уравнение координаты точек С и В. Получим:

Сравнивая полученные величины прогибов, приходим к выводу, что прогиб в сечении В больше, чем прогиб в сечении С в 3,2 раза:

Пример 31.

В сколько раз угол поворота сечения А на конце изображенной на рис.6.42.4 балки больше, чем угол поворота сечения В на расстоянии четверти пролета от левого конца балки?

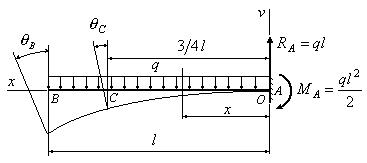
Рис. 6.42.4

Решение.

1. Находим реакции:

2. Выбираем начало координат O на правом конце балки, совмещая его с точкой А. Ось Ov направляем вверх, ось Ox - влево.

3. Записываем выражение для изгибающего момента в сечении x:

4. Составляем приближенное дифференциальное уравнение упругой линии балки:

Знак “+” в уравнении упругой лиинии был принят потому, что ось Ov направлена вверх.

5. Принимаем жесткость балки постоянной. Интегрируем дифференциальное уравнение. Получаем:

Постоянную интегрирования C в уравнении (д) найдем из условия, что при x=0 угол поворота в сечении А равен нулю. Подставим в уравнение (д) x=0 и приравняем нулю угол поворота сечения А. Получим C=0. Тогда окончательно уравнение для угла поворота принимает вид:

6. Подставляем в уравнение (е) координату , получим угол поворота в сечении С:

7. Подставляем в уравнение (е) координату x=l. Получим угол поворота в сечении В:

8. Сравнивая углы поворота в сечениях В и С, получим:

Таким образом, угол поворота в сечении В в 1,016 раза больше, чем угол поворота в сечении С.

Пример 32.

Найти стрелу прогиба (в мм) балки, изображенной на рис. 6.42.5, если жесткость поперечного сечения балки равна 36000 кНм².

Рис

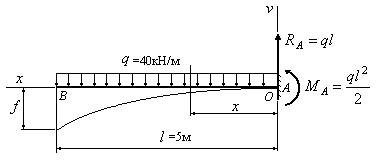
Рис. 6.42.5

Решение.

Воспользуемся решение задачи, ход которого изложен в примере 31 и проинтегрируем выражение (д). Получим уравнение для прогиба в сечении x:

Постоянные интегрирования в уравнении (ж) получим, воспользовавшись граничными усорвиями закрепления балки, в соответствии с которыми прогиб и угол поворота в жесткой заделке равны нулю:

при x=0 v=0 и θ=0.

Подставляя x=0 в уравнения (д) и (ж) и приравнивая последовательно нулю угол поворота и прогиб нулю, получим: C=0; D=0. Тогда выражение для прогиба принимает вид:

Подставляя в это уравнение заданные значения жесткости сечения, интенсивности распределенной нагрузки, длину балки, а также координату сечения В, в котором определяется стрела прогиба (x=l), находим:

Знак “-” у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси Ov.

Пределы применимости приближенной теории изгиба балок

При выводе дифференциального уравнения изогнутой оси балки (28) выражение для кривизны χ=1/ρ балки было выбрано приближенно. Выясним степень точности приближенного уравнения (27). Для этого рассмотрим задачу о чистом изгибе консольной балки (рис. 6.43).

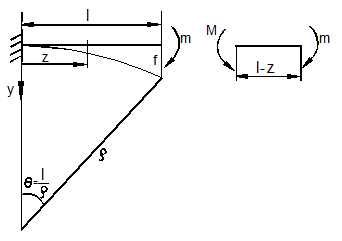
Рис. 6.43

В этом случае и поэтому . Из рис. 6.43 прогиб на конце консоли:

Разложим косинус в ряд и ограничимся тремя первыми элементами:

Выражение для прогиба f принимает вид:

или с учетом и (7):

Дадим теперь приближенное решение задачи. Интегрируя уравнение

При M_x=-m, получаем:

Так как при z=0 прогиб , угол поворота , то

При z=l на конце консоли прогиб:

Сравнивая решения (36), (37), находим:

Удовлетворимся при определении прогибов по приближенной теории точностью в 3%. Полагая

получаем:

Таким образом, приближенное дифференциальное уравнение (27) изогнутой оси упругой балки дает достаточную точность решения задачи даже в том случае, когда прогиб составляет 30% от длины стержня. Такие прогибы возможны только у очень гибких балок большой длины или очень малой толщины типа гибкой стальной линейки.

Общие дифференциальные соотношения при изгибе

Ранее были получены дифференциальные зависимости между интенсивностью распределенной нагрузки q(x), поперечной силой Q(x) и изгибающим моментом M(x):

Кроме того, были получены дифференциальные зависимости между прогибом и углом поворота, прогибом и изгибающим моментом, углом поворота сечения и изгибающим моментом:

Эти зависимости, после некоторого преобразования, можно расположить последовательно:

Из этих уравнений видно, что, зная нагрузку q(x) и устройство опор балки, можно последовательным интегрированием получить величины Q(x), M(x), EJθ(x), EJv(x). С другой стороны, зная уравнение упругой линии, можно путем последовательного дифференцирования по x из функции EJv(x) получить EJθ(x), M(x), Q(x) и q(x). Для графического изображения этих зависимостей условимся положительные значения всех перечисленных величин откладывать вверх, а отрицательные – вниз; положительное направление оси в правой системе координат примем вправо, поворот сечения по часовой стрелке – отрицательным, а против – положительным. В левой системе координат – наоборот.

Приведем несколько примеров построения эпюр распределения поперечных сил, изгибающих моментов, углов поворота сечений и прогибов.

Пример 33.

Построить качественные эпюры распределение поперечных сил, изгибающих моментов, углов поворота сечений и прогибов, для балки, изображенной на рис. 6.44.1.

Рис

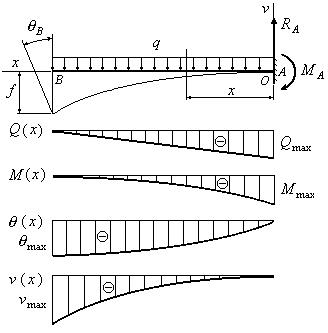
Рис. 6.44.1

Пример 34.

Построить качественные эпюры распределения поперечных сил, изгибающих моментов, углов поворота сечений и прогибов, для балки, изображенной на рис. 6.44.2.

Рис

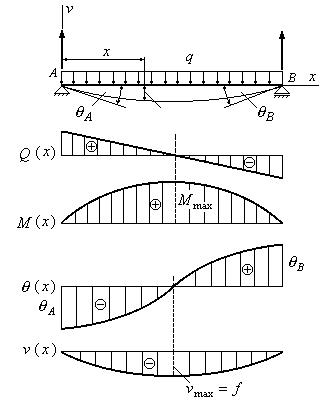
Рис. 6.44.2

Пример 35.

Построить качественные эпюры распределения поперечных сил, изгибающих моментов, углов поворота сечений и прогибов, для балки, изображенной на рис. 6.44.3.

Рис

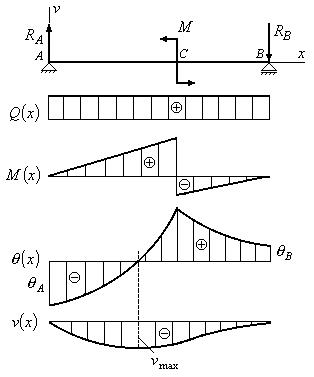
Рис. 6.44.3

При построении эпюр углов поворота и прогибов следует придерживаться некоторых правил. Сформулируем их:

1. Так как M(x) представляет собой диаграмму производной от эпюры углов поворота θ, то ординаты эпюры M пропорциональны тангенсу угла наклона касательной к эпюре θ. В сечениях, где M(x)=0, касательная к кривой θ=F(x) должна быть параллельна оси абсцисс (рис.6.44.1 - сечение А и рис.6.44.2 - сечения А и В). Скачку на эпюре моментов соответствует угловая точка на эпюре θ (рис.6.44.1 – сечение А и рис.6.44.3 – сечение С).

2. Вторая производная прогиба

имеет знак момента. Если момент положителен (сжаты верхние волокна), то вогнутость на эпюре v будет обращена в сторону положительных прогибов v (вверх). При отрицательном моменте вогнутость пораболы обращена вниз. Так как ординаты эпюр изгибающих моментов мы условились откладывать со стороны сжатых волокон, то вогнутость эпюры прогибов v всегда обращена в ту сторону, с которой расположены ординаты эпюры изгибающих моментов.

3. Вторая производная угла поворота

имеет знак поперечной силы. Если Q положительна, то выпуклость на эпюре θ будет обращена вниз (рис.6.44.1 и рис. 6.44.2). При Q <0 выпуклость направлена в сторону оси Oy, т.е. вверх (рис.6.44.2). В сечении, где Q меняет знак, на эпюре θ наблюдается точка перегиба. (рис.6.44.2).

4. Если изгибающий момент равен нулю на протяжении какого-либо участка балки, то на этом участке угол поворота не меняется, а прогиб меняется по линейной зависимости.

5. На тех участках балки, где эпюра M изменяется по линейному закону, эпюра θ меняется по закону квадратной параболы, а эпюра v - по закону параболы третьего порядка. Там, где эпюра M изменяется по закону квадратной параболы, эпюра θ меняется по закону параболы третьего порядка, а эпюра v - по закону параболы четвертого порядка.

6. На участках, где действует постоянный момент, эпюра θ меняется по линейному закону, а эпюра прогибов меняется по закону квадратной параболы.

7. Так как θ представляет собой график изменения по длине балки тангенсов наклона касательных к упругой линии, то можно утверждать следующее:

а) на участках, где в направлении оси Ox прогиб v возрастает, угол наклона θ будет положителен. Наоборот, при уменьшении v углы наклона θ будут отрицательны (рис.6.44.3, участок АС);

б) в сечениях, где θ=0, касательная к эпюре v горизонтальна, т.е. в этом сечении на эпюре v наблюдается аналитический максимум или минимум (рис.6.44.3).

Рассмотрим еще несколько примеров построения эпюр углов поворота и прогибов.

Пример 36.

Какая из эпюр углов поворота соответствует приведенной на рис.6.44.4 эпюре изменения прогибов, представляющей собой параболу четвертого порядка?

Рис

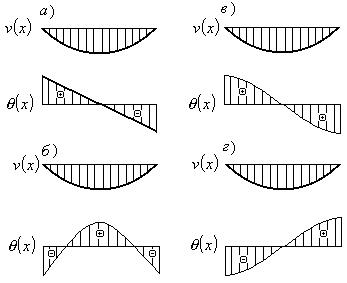
Рис. 6.44.4

Решение.

Вариант а) отпадает, так как эпюра углов поворота θ может меняться по линейному закону лишь в том случае, если эпюра прогибов v представляет собой квадратную параболу.

Вариант б) не подходит по той причине, что максимального значения прогиб достигает в сечении, в котором угол поворота равен нулю. Такого соответствия в этом варианте нет.

Вариант в) не подходит, так как на левой части эпюры v(x) прогиб убывает слева направо при положительном тангенсе угла наклона касательной к кривой прогибов. В этом варианте нет соответствия между знаком приращения прогиба и знаком эпюры углов поворота.

Вариант г) подходит по ряду признаков: во-первых, совпадают знаки приращения прогиба и знаки угла поворота на всей длине участка. Во-вторых, экстремального значения прогиб достигает в сечении, в котором угол поворота равен нулю. В-третьих, в сечениях на левом и правом концах участка, там, где прогиб равен нулю, касательная к кривой углов поворота параллельна базисной линии, что соответствует равенству нулю тангенса угла поворота в этих сечениях.

Таким образом, из четырех вариантов эпюра изменения углов поворота соответствует эпюре изменения прогибов в последнем варианте.

Пример 37.

Какая из эпюр прогибов соответствует представленной на рис.6.44.5 эпюре изгибающих моментов, если положительное направление оси Oy направлено вверх?

Рис

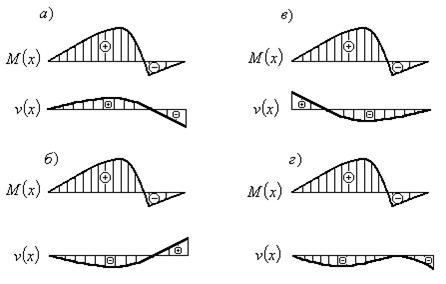
Рис. 6.44.5

Решение.

Вариант а) не подходит, так как положительному изгибающему моменту в выбранной ситеме координат должна соответсвовать положительная кривизна упругой линии балки. Такого соответствия здесь нет.

Вариант б) не подходит по той причине, что изогнутая ось балки имеет кривизну одного и того же знака на всей длине участка, в то время как изгибающий момент меняет знак по длине участка.

Вариант в) не подходит по той же причине.

Вариант г) подходит, так как имеет место соответствие знаков изгибающего момента и знаков кривизны изогнутой оси на соответствующих участках.

Интегрирование дифференциального уравнения изогнутой оси балки методом начальных параметров

Этот метод определения перемещений в балках относится также к методам аналитическим. При использовании метода непосредственного интегрирования упругой линии балки нам приходилось определять постоянные интегрирования С и D. При одном участке таких постоянных было две. С увеличением числа участков количество постоянных интегрирования растет вдвое. Так, если балка по условиям нагружения имеет n участков, то интегрирование дифференциальных уравнений для всех участков балки дает 2n произвольных постоянных. Из граничных условий опирания балки можно найти всего 2 постоянные интегрирования. Остальные 2(n-1) постоянные приходится определять из условия непрерывного и плавного сопряжения для всех участков упругой линии. В результате мы получаем систему уравнений степени 2n, решение которой уже при n>3 вызывает серьезные сложности, учитывая процедуру составления дополнительных уравнений совместности деформаций. Эта громоздкая и кропотливая работа делает метод непосредственного интегрирования практически неприменимым для балок с большим числом участков.

Между тем, существует возможность решения подобных задач путем сведения всех постоянные интегрирования к двум независимо от числа участков. Этот метод получил название метода начальных параметров. Разработан этот метод советскими учеными Пузыревским Н.П., Куликовским П.Г., Снитко Н.К., Безухим Н.И., Уманским А.А. и др.

Рассмотрим балку, нагруженную силами и моментами P, q, m (рис. 6.45). Силы P, q считаем положительными, если они направлены в положительном направлении координатной оси у, т.е. вниз. Момент m считаем положительным, если он вращает сечение балки против часовой стрелки, когда мы смотрим на него с конца положительной оси x, ортогональной к плоскости yx. В этом случае прогибы v(z) любой точки оси стержня с координатой z направлены вниз по оси у.

Рис. 6.45

Балку по длине можно разбить на несколько участков, на которых аналитические выражения изгибающих моментов будут различны.

Границей этих участков являются те сечения, над которыми к балке приложены сосредоточенные силы Р, момент m либо меняется характер нагружения так, как в сечении z=c, с которого начинается действие распределенной нагрузки q(z).

Интегрируем дважды дифференциальное уравнение изогнутой оси балки (27):

В результате получаем:

где v₀, θ₀ - прогиб и угол поворота сечения в начале координат при z=0, называемые начальными параметрами задачи по определению перемещений. Вычислим в (38) интеграл:

при одновременном действии P, q, m считая жесткость EJ_x при изгибе постоянной величиной. Для этого найдем аналитические выражения момента M_x(z) для двух сечений от каждого внешнего силового воздействия. Пусть первое сечение z лежит левее рассматриваемой внешней силы или момента, а второе - правее. Тогда получаем (см. рис. 6.45):

Полагая последовательно при почленном интегрировании dz=d(z-a)=d(z-b)=d(z-c), получаем:

Интегрируя полученное выражение еще раз, найдем:

Подставляя полученные выражения интегралов в (38), получим формулы:

называемые универсальными для угла поворота сечения и прогиба точки оси балки.

Если распределенная нагрузка q(z) не является постоянной, то ее можно разложить в ряд Тейлора в окрестности значения z=c:

где - факториал числа n.

В этом случае после интегрирования (38) получаем:

При наличии в балке внутреннего шарнира К в сечении z=dk первая производная от прогиба v по z претерпевает в этом случае скачок на величину ∆θ_k (рис. 6.45.1) так, что:

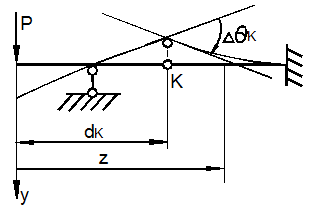
Рис. 6.45.1

Интегрируя, получаем:

Обобщенные силы m, P, q в (41), (43) повторяются столько раз, сколько они рассматриваются в рассматриваемой задаче. Если распределенная нагрузка не доходит до рассматриваемого сечения с координатой z, то ее следует продолжить до этого сечения и добавить точно такую же, но противоположного знака (см. рис. 6.45).

Характерной особенностью метода начальных параметров является то, что для определения перемещения нет необходимости составлять и интегрировать дифференциальное изогнутой оси балки. Достаточно составить универсальное уравнение упругой линии, из условий на опорах найти начальные параметры и снова воспользоваться универсальным уравнением, чтобы найти прогиб в рассматриваемом сечении.

Порядок расчета по методу начальных параметров:

Чтобы определить перемещения методом начальных параметров надо:

1. Определить опорные реакции.

2. Выбрать начало отсчета.

3. Определить начальные параметры из условий закрепления.

4. Подсчитать перемещения линейные или угловые, пользуясь формулами методов начальных параметров.

Простейшие статически неопределимые задачи при изгибе. Метод сравнения (наложения) перемещений

Рассмотрим простейшую один раз статически неопределимую балку (рис. 6.46).

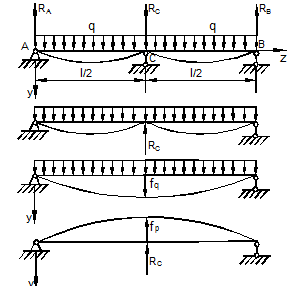
Рис. 6.46

Прогиб балки над опорой С равен нулю и его можно, в силу принципа независимости действия сил, представить как сумму перемещений от распределенной нагрузки и сосредоточенной силы R_c:

Используя известные решения, имеем:

Следовательно,

откуда

Из уравнений равновесия:

находим опорные реакции

В поперечном сечении z

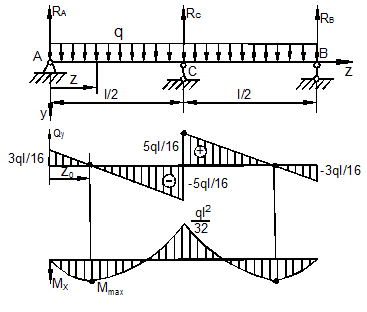
Рис. 6.47

Экстремальный момент возникает в сечении с координатой , которая находится из условия:

откуда . Максимальный момент

Он меньше, чем момент над средним сечением при z=l/2:

На рис. 6.47 построены эпюры Q_y и M_x.

Расчет на прочность простейших статически неопределимых балок методом допускаемых нагрузок

Рассмотрим простейшую статически неопределимую балку (рис. 6.48,а).

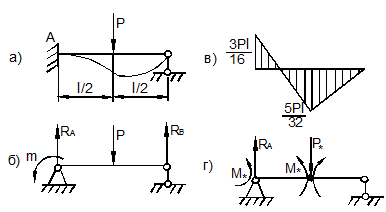
Рис. 6.48

Расчет на прочность по допускаемым напряжениям состоит в том, чтобы найти и потребовать . Для этого сначала необходимо раскрыть статическую неопределимость задачи. На рис. 6.48,б изображена эквивалентная балка, в которой момент m должен быть подобран так, чтобы угол поворота в опоре А обращался в нуль как и в исходной схеме балки (рис. 6.48,а).

Вычислим угол поворота в опоре А:

откуда находим:

Максимальный момент возникает в защемлении (рис. 6.48, в):

Таким образом, условие прочности по допускаемым напряжениям (или расчетному сопротивлению) дает:

откуда

Предельная нагрузка P_t упругого состояния, при которой впервые в балке возникает пластическая деформация, равна:

Первый пластический шарнир образуется в защемлении. В этом пластическом шарнире . Однако балка будет испытывать стеснённую пластическую деформацию, пока в середине пролета под силой Р момент также не будет равным и балка превратится в механизм (рис. 6.48, г). Для предельного состояния имеем уравнения равновесия:

откуда следует

Допускаемое значение внешней нагрузки:

Сравнивая и P_t либо и получим, что их отношение:

Статическая неопределимость задачи повышает допустимую нагрузку на 12,5%. Для балки прямоугольного сечения . В случае прямоугольника . Для данной задачи обнаруживается резерв прочности в 69% по сравнению с расчетом по допускаемым напряжениям.

В рассматриваемом примере пластические шарниры образуются в защемлении и в сечении под сосредоточенной силой. В случае распределенной нагрузки указать сразу сечения, где возникнут пластические шарниры, не всегда удается. Рассмотрим простейшую двухпролетную статически неопределимую балку (рис. 6.49). Выше эта задача была решена для случая упругого поведения балки и построена эпюра моментов (рис. 6.47).

Рис. 6.49

Момент в среднем сечении, при котором в крайних волокнах возникают пластические деформации:

откуда соответствующая предельная нагрузка равна:

Рассмотрим предельное состояние балки. Первый пластический шарнир образуется над средней опорой. Два других - в сечениях, строго говоря, не совпадающих с сечениями, где действуют максимальные моменты. Обозначим расстояние от левой опоры до первого шарнира в пролете через . Тогда уравнение равновесия балки левее первого и второго шарниров будет иметь вид:

откуда после исключения R_A следует:

Разрушающая предельная нагрузка оказывается зависящей от величиины ξ, т.е. местоположения пластического шарнира в пролете. Дифференцируя данное выражение для q по ξ и приравнивая производную нулю, получим:

откуда

Так как , то перед радикалом следует сохранить знак плюс. Тогда В результате получим:

Сравнивая выражения для и , находим:

Следовательно, в данной задаче статическая неопределимость повышает допустимую нагрузку на 45,7%. Если балка имеет прямоугольное сечение, то W_*/W_x=1,5. Поэтому в данной задаче полное увеличение допускаемой нагрузки составляет , т.е. 118,6%. Если заменить в каждом из пролетов распределенную нагрузку q их равнодействующими ql/2 приложенными в их середине, т.е. при , то получим:

Величина

что отличается от точного решения всего на 2,94%. Для прямоугольного сечения получаем k = 2,25 вместо 2,186.

Изгиб балок переменного поперечного сечения

На практике часто приходится иметь дело со стержнями переменного поперечного сечения, у которых площадь F(z) и момент инерции являются функциями z. В этом случае общий интеграл дифференциального уравнения изогнутой оси балки имеет вид:

Обозначим символом момент инерции какого-либо сечения, например при z = 0. Введем обозначение:

Тогда (41) можно представить в виде

где

Исходная балка переменной жесткости приводится к балке постоянной с некоторым моментом .

Рассмотрим в качестве примера балку ступенчато-переменного сечения с двумя участками разной жесткости и (рис. 6.50).

а) б)

Рис. 6.50

Пусть длины участков

Тогда

Для исходной балки Для приведенной к единой жесткости балки имеем:

где

Как видно, на границе участков при внутренние силовые факторы приведенной балки претерпевают скачки на величины:

Это возможно для приведенной балки только в том случае, если на стыке участков при z₁=z₂=l/2 будут приложены внешние сосредоточенные сила ∆P и момент ∆m равные:

Дальнейшее решение задачи по определению прогибов в балке состоит в применении метода начальных параметров к балке с приведенной жесткостью EJ_x. Прогиб балки на конце консоли второго участка будет равен:

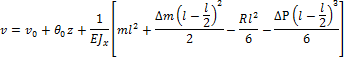
Так как при , то после замены R=P, получаем:

Балка равного сопротивления

Пусть балка имеет прямоугольное переменное сечение, для которого высота сечения h - постоянная величина, а ширина изменяется по линейному закону:

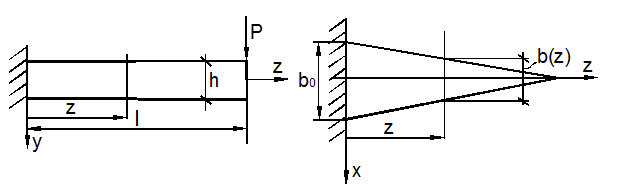
Рис. 6.51

Момент инерции поперечного сечения:

Для рассматриваемой балки изгибающий момент в поперечном сечении z равен:

Согласно (23) прогиб балки:

или с учетом

Определим теперь максимальные напряжения по формуле:

Полагая y_max=h/2 и используя выражения для M_x и J_x найдем:

где - момент сопротивления сечения в защемлении на левом конце балки при z = 0.

Таким образом, во всех сечениях балки рассматриваемого поперечного сечения максимальные поперечные сечения максимальные напряжения получились одинаковыми. Такая балка носит название балки равного сопротивления изгибу. Изогнутая ось балки представляет собой квадратичную параболу.

Балка на упругом основании

Если балка лежит на упругом основании, то последнее оказывает на балку реактивное давление q₀=-kv (гипотеза Винклера), где k - коэффициент упругости основания (коэффициент постели). Добавляя в правую часть уравнения нагрузку q₀=-kv, получим дифференциальное уравнение изогнутой оси балки на упругом основании:

Введем обозначение:

Тогда уравнение (45) принимает вид:

Его общим решением будет:

где - частное решение неоднородного уравнения (45).

Так как:

то общее решение (27) можно записать в ином виде:

Академик А. Н. Крылов ввел функции:

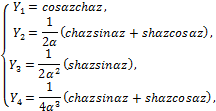
обладающие свойством:

Они образуют систему частных решений уравнения с единичной матрицей, представляемой в виде табл. 6.1.

Общее решение уравнения (45) можно записать через функции Крылова в виде

где

Таблица 6.1

	Y(0)	Y’(0)	Y’’(0)	Y’’’(0)
Y₁	1	0	0	0
Y₂	0	1	0	0
Y₃	0	0	1	0
Y₄	0	0	0	1

Рассмотрим балку полубесконечной протяженности (рис. 6.52).

Рис. 6.52

На краю балки при z=0 действуют сосредоточенные сила Р и момент m. Следовательно, на край балки при z = 0 имеем перерезывающую силу и изгибающий момент . Если балка весьма длинная, то при больших z (теоретически ) прогибы должны быть весьма малыми (теоретически ). Поэтому, согласно (47), . Так как распределенная нагрузка q=0, то частное решение .

Следовательно, общее решение рассматриваемой частной задачи имеет вид:

Вычислим производные:

Зная их, можно вычислить изгибающий момент и перерезывающую силу:

Постоянные C₁, C₂ определяем из граничных условий при z=0:

откуда с учетом (48), (49) получаем:

Для прогиба (48) получаем выражение:

Максимальный прогиб находим из (49) при z=0:

Пусть на краю балки при z=0 момент , а перерезывающая сила Q₀=-P, тогда:

Как видно, прогиб v, момент M_x, сила Q_y по мере удаления от края балки z=0 периодически уменьшаются по экспоненциальному закону. Эта особенность быстрого затухания v, M_x, Q_y по мере удаления от края балки называется краевым эффектом (см. рис. 6.52).

Изгиб составных балок

Работу составных балок проиллюстрируем на простом примере трехслойной балки прямоугольного поперечного сечения. Если слои между собой не связаны и силы трения между ними отсутствуют, то каждый из них деформируется как отдельная балка, имеющая свой нейтральный слой (рис. 6.53,а). Нагрузка между этими балками распределяется пропорционально их жесткостям при изгибе (в данном примере поровну). Это означает, что моменты инерции и моменты сопротивления трех независимо друг от друга деформирующихся балок должны быть просуммированы

Если скрепить балки сваркой, болтами или другим способом (рис.6.53,б), то с точностью до пренебрежения податливостью наложенных связей сечение балки будет работать как монолитное с моментом инерции и моментом сопротивления, равным

Как видно, при переходе к монолитному сечению жесткость балки возрастает в девять раз, а прочность—в три раза. В инженерной практике наиболее распространены сварные двутавровые балки.

image003-19

а) б)

Рис.6.53. Расчетные схемы составных балок: а) несвязанная конструкция, б) связанная сварная конструкция

Вопросы для самопроверки

- Что называется балкой?

- Какой вид нагружения называется изгибом?

- Какой изгиб называется чистым, поперечным?

- Какой изгиб называют чистым, поперечным, прямым и косым?

- Чем отличается чистый изгиб от поперечного изгиба, прямой изгиб от косого изгиба?

- Сформулируйте определение «поперечный изгиб»?

- Сформулируйте понятие «чистый изгиб»?

- Какую плоскость называют силовой?

- Что понимается под волокнами бруса? В чем сущность гипотезы плоских сечений и допущения о ненадавливании волокон друг на друга?

- Что такое нейтральная линия, силовая линия?

- Какие внутренние усилия возникают в поперечных сечениях балки в общем случае действия на неё плоской системы сил?

- Как формулируется гипотеза плоских сечений?

- Что представляет собой нейтральный слой и нейтральная ось?

- Чему равна кривизна оси балки при чистом изгибе?

- По какой кривой изгибается балка при чистом изгибе?

- Докажите, что при прямом изгибе нейтральная линия является центральной главной осью поперечного сечения бруса?

- Какие силовые факторы возникают в сечении балки при чистом изгибе?

- Какие силовые факторы возникают в сечении при поперечном изгибе?

- Какой силовой фактор вызывает изгиб бруса? Охарактеризуйте тип деформации бруса при изгибе? Что такое нейтральный слой?

- Что такое изгибающий момент (M_х)? Выразите M_х через напряжения в рассматриваемом сечении? Как определяется M_х через внешние силы?

- Что такое поперечная сила (Q_y)? Как определяется Q_y через внешние силы?

- Чем отличается статически определимая балка от статически неопределимой?

- Для чего в многопролетных балках вводятся промежуточные шарниры?

- Какие виды нагрузок могут действовать на балку?

- Какие виды опор встречаются при расчете балок? Чем они отличаются?

- Что подразумевается под понятием «поперечная сила»? как она определяется?

- Какое правило законов для определения поперечной силы используется?

- Сформулируйте определения понятия «изгибающий момент, действующий в сечении балки»?

- Каково правило законов для определения изгибающего момента используется?

- Как вычисляется изгибающий момент в поперечном сечении балки?

- Как вычисляются поперечная и продольная силы в поперечном сечении балки?

- Как определить значение поперечной силы и изгибающего момента в произвольном сечении балки?

- Как определить знаки поперечной силы и изгибающего момента?

- Какие уравнения используются для определения значений опорных реакций?

- Как проверить правильность определения опорных реакций?

- Как формулируется гипотеза плоских сечений?

- Что представляют собой нейтральный слой и нейтральная линия и как они расположены?

- По какой формуле определяются нормальные напряжения в поперечном сечении балки при чистом изгибе и как они изменяются по высоте балки?

- Что называется моментом сопротивления при изгибе и какова его размерность?

- Для чего строят эпюры внутренних силовых факторов?

- Как можно контролировать построение эпюр поперечных сил Q и изгибающих моментов М?

- Опишите особенности очертания эпюр M_х и Q_y: в каких сечениях наблюдаются скачкообразные изменения ординат в эпюре M_х; на каких участках эпюра M_х — линейная функция, a Q_y = const, почему в местах приложения поперечной сосредоточенной силы в эпюре Q_y — скачок, а в эпюре M_х — «излом» направления касательной; почему в сечениях, в которых M_х имеет экстремальные значения, Q_y = 0 или проскакивает через нулевое значение?

- Если эпюра поперечной силы ограничена наклонной прямой, как выглядит эпюра изгибающего момента?

- Как определить положение экстремального значения изгибающего момента при действии распределенной нагрузки на участке балки?

- Распределенная нагрузка направлена вверх. Как выглядит парабола, очерчивающая эпюру изгибающих моментов вдоль оси бруса?

- Какой линей очерчена эпюра изгибающих моментов, если закон их изменения по длине балки выражается уравнением: ?

- Как находят равнодействующую распределенной нагрузки (величина, положение)?

- Запишите дифференциальные и интегральные зависимости между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки при поперечном изгибе прямого стержня.

- В каком случае эпюра изгибающего момента выпукла? Вогнута?

- В каком случае эпюра изгибающего момента имеет экстремум?

- В каком случае эпюра поперечной силы постоянна?

- По какому закону изменяется поперечная сила на участке стержня при наличии равномерно распределенной нагрузки? Изгибающий момент?

- По какому закону изменяется поперечная сила на участке стержня при отсутствии равномерно распределенной нагрузки? Изгибающий момент?

- Как с помощью эпюры поперечных сил определить положение сечения с экстремальным значением изгибающего момента?

- Как определить равнодействующую распределенной нагрузки (величину и положение)?

- Каким образом можно убедиться, что опорные реакции найдены верно?

- Запишите условия равновесия, которым должны удовлетворять приложенные к стержню нагрузки.

- Какая нагрузка вызывает скачок на эпюре поперечной силы?

- Какая нагрузка вызывает скачок на эпюре изгибающего момента?

- Какая нагрузка вызывает излом на эпюре изгибающего момента?

- По какому закону изменяется поперечная сила на участке стержня при отсутствии распределенной нагрузки? Изгибающий момент?

- Как находят опасные сечения?

- Какими зависимостями связаны изгибающий момент, поперечная сила и интенсивность распределенной нагрузки? Как эти зависимости используют при проверке правильности построения эпюр поперечных сил и изгибающих моментов?

- Получите дифференциальные зависимости между изгибающим моментом (M_х), поперечной силой (Q_y) и интенсивностью внешней нагрузки q?

- В какой последовательности строят эпюры поперечных сил и изгибающих моментов?

- Почему для определения значения поперечной силы и изгибающего момента в произвольном сечении балки на двух опорах необходимо знать реакции опор?

- Можно ли для двухопорной балки определить внутренние усилия без вычисления реакций опор?

- Почему при построении эпюр Q, M для балки, защемлённой одним концом, можно не определять реакции опоры?

- Какая дифференциальная зависимость связывает q, Q и M?

- Как изменяется поперечная сила в сечении балки, к которому приложена сосредоточенная сила? Как изменяется значение изгибающего момента в сечении балки, к которому приложен сосредоточенный момент?

- Как определить максимум и минимум эпюры изгибающих моментов?

- Как изменяются нормальные напряжения по высоте балки при чистом изгибе?

- Как определить максимальные нормальные напряжения при изгибе?

- Какие геометрические характеристики сечения используют для определения нормальных напряжений при изгибе? Как определяют момент сопротивления при изгибе и какова его размерность?

- Что называют моментом сопротивления сечения при изгибе и какова его размерность?

- В каких случаях при поперечном изгибе допустимо нормальные напряжения определять по формуле, полученной для случая чистого изгиба?

- По какому закону изменяются касательные напряжения по высоте балки прямоугольного сечения?

- Какие формы поперечных сечений являются рациональными для балок из пластичного материала?

- Какой должна быть рациональная форма сечения для балки из хрупкого материала?

- Как проводится проектировочный расчет для балки заданной формы сечения?

- В каких случаях следует производить дополнительный поверочный расчет по наибольшим касательным напряжениям?

- Какие допущения положены в основу вывода формулы для определения нормальных напряжений при изгибе?

- Получите соотношение между величиной изгибающего момента и кривизной изогнутой оси бруса?

- Получите формулу нормальных напряжений при изгибе? Охарактеризуйте эпюру напряжений, величину наибольших нормальных напряжений, момента сопротивления сечения балки при изгибе?

- Получите формулу сдвигающей силы в продольных сечениях бруса при изгибе. Как используется эта формула при расчете составных сечений балок?

- Получите формулу касательных напряжений при изгибе? Охарактеризуйте параметры, входящие в эту формулу, и постройте эпюры напряжений для прямоугольного и двутаврового сечений бруса?

- Приведите формулировку и аналитическую запись условия прочности при изгибе?

- Покажите, как используется условие прочности при подборе сечения балки, определения допустимой величины изгибающего момента при заданном сечении балки, проверку прочности балки при заданной нагрузке?

- Как распределяются нормальные напряжения по поперечному сечению балки? В каких точках сечения они достигают наибольшего значения?

- Напишите формулу для определения нормального напряжения при изгибе в любой точке поперечного сечения?

- Напишите формулы для определения момента инерции и момента сопротивления для прямоугольника. Что характеризуют эти величины? Укажите единицы измерения этих величин?

- Напишите условие прочности при изгибе?

- Подберите размеры поперечного сечения балки в виде швеллера? Максимальный изгибающий момент 15кНм; допускаемое напряжение материала балки 160 МПа.

- Почему при поперечном изгибе в продольных сечениях балки возникают касательные напряжения?

- Какой материал называют хрупким?

- В чем особенность механических характеристик хрупких материалов по сравнению с пластичными?

- Какой вид имеют условия прочности по допускаемым напряжениям при прямом изгибе балки, выполненной из пластичного материала? Из хрупкого материала?

- Какая из зон сечения балки из неравнопрочного материала должна быть больше по высоте – зона растянутых или зона сжатых волокон?

- Каким опытом можно подтвердить возникновение касательных напряжений в продольных сечениях балки?

- Что представляет собой нейтральная линия сечения? Как определить ее положение?

- В каких точках поперечного сечения возникают при поперечном изгибе балки наибольшие касательные напряжения? Как их определить?

- Как составляют условие прочности балки при изгибе?

- Дифференциальные зависимости при изгибе.

- Правило знаков при построении эпюр.

- По какой формуле определяются нормальные напряжения в поперечных сечениях балки при поперечном изгибе?

- Сформулируйте теорему Д.И. Журавского?

- Какое напряжение в сечении балки вызывает поперечная сила?

- Какое напряжение в сечении балки вызывает изгибающий момент?

- Запишите формулу для определения касательных напряжений в поперечных сечениях балки при прямом поперечном изгибе?

- Как распределяются нормальные напряжения по высоте сечения балки?

- Как распределяются касательные напряжения по высоте сечения балки?

- Как записываются условия прочности при поперечном изгибе балки по нормальным напряжениям?

- Как записываются условия прочности при поперечном изгибе балки по касательным напряжениям?

- Какова разница в расчетах балок по допускаемой нагрузке и по допускаемым напряжениям?

- Как производится проверка прочности балки по главным напряжениям?

- Как определяется потенциальная энергия при поперечном изгибе?

- Как ведется расчет балок по разрушающей нагрузке?

- Какой вид имеют эпюры касательных напряжений в поперечных сечениях прямоугольной и двутавровой формы?

- Как находятся главные напряжения при изгибе?

- Как направлены главные площадки на уровне нейтрального слоя и в точках, наиболее удаленных от этого слоя?

- Что представляют собой траектории главных напряжений?

- Прогибы и углы поворота при изгибе.

- Какие формы поперечных сечений являются рациональными для балок из пластичных материалов?

- Какие перемещения получают поперечные сечения балок при прямом изгибе?

- Что называется упругой линией балки?

- Какие виды перемещений получают поперечные сечения балки при изгибе балок?

- Что называется прогибом балки?

- Какая зависимость между прогибами и углами поворота сечений балки?

- На основании каких соображений точное дифференциальное уравнение прогибов балки заменяется приближенным?

- Выведите дифференциальное уравнение упругой линии балки?

- Сколько произвольных постоянных вводится при интегрировании уравнения прогибов и как они определяются?

- Запишите основное дифференциальное уравнение изогнутой оси балки.

- Какими величинами характеризуется при поперечном изгибе жесткость балки?

- Как записывается приближенное дифференциальное уравнение изогнутой оси балки?

- Что называют упругой линией балки?

- Какая зависимость существует между радиусом кривизны упругой линии ρ, изгибающим моментом М_х и жесткостью балки EJ_x?

- Как записать дифференциальное уравнение упругой линии? Из каких условий определяют постоянные при его интегрировании?

- Как вычисляют потенциальную энергию деформации, накапливаемую в балке при изгибе?

- Объясните смысловую сторону метода непосредственного интегрирования?

- Как записывается универсальное уравнение упругой линии балки?

- Что называется жесткостью сечения при изгибе?

- Как из основного (приближенного) дифференциального уравнения изогнутой оси балки получаются выражения углов поворота и прогибов ее сечений?

- Из каких условий определяются постоянные интегрирования, входящие в уравнение углов поворота и прогибов сечений балки?

- Какие перемещения получают поперечные сечения балок при изгибе?

- Почему при определении прогибов балки можно пользоваться приближенным дифференциальным уравнением изогнутой оси балки?

- Из каких граничных условий определятся постоянные интегрирования при нахождении прогибов балки?

- Что представляет собой уравнение метода начальных параметров?

- Что называют композитным брусом?

- Чем можно объяснить существенное отличие нормальных напряжений в элементах разнородной упругости при изгибе композитного бруса?

- Чем определяется предельное состояние балки при изгибе?

- Изгиб называется чистым, если в поперечных сечениях балки из шести внутренних усилий действуют только …

- При изгибе возникают такие перемещения, как …

- При поперечном изгибе в поперечных сечениях балки возникают такие напряжения, как …

- Дифференциальная зависимость между изгибающим моментом и поперечной силой имеет вид …

- Когда изгибающий момент на участке с распределенной нагрузкой имеет экстремальное значение, поперечная сила в этом сечении равна …

- Нормальные напряжения в любой точке поперечного сечения балки определяются по формуле …

- Наибольшие нормальные напряжения в поперечном сечении балки возникают в …

- Условие прочности по нормальным напряжениям при изгибе имеет вид …

- Касательные напряжения при поперечном изгибе в любой точке поперечного сечения балки определяется по формуле ...

- Касательные напряжения при поперечном изгибе достигают максимума на …

- Условие прочности по касательным напряжениям при изгибе имеет вид …

- При упругом деформировании нейтральная линия сечения балки проходит через …

- Момент сопротивления изгибу балки прямоугольного сечения размером h×в относительно центральной оси, параллельной основанию в равен …

- При подборе сечения балки, его момент сопротивления должен быть не менее …

- Моментом сопротивления изгибу поперечного сечения балки называют отношение …

- Приближенное дифференциальное уравнение упругой линии балки имеет вид …

- Между прогибом и углом поворота сечения балки существует дифференциальная зависимость в виде …

- При использовании в расчетах прогибов метода начальных параметров, сами начальные параметры находят из граничных условий на …

- Если левый конец балки жестко защемлен, то начальные параметры равны …

- Условие жесткости при изгибе имеет вид …

- Укажите правильный вариант записи силового граничного условия. Для выбранного варианта впишите кинематические граничные условия.

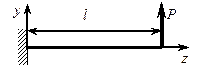
1. Q_y(l)=-P, M_x(l)=0, ____________________________________

2. Q_y(l)=P, M_x(l)=0, _____________________________________

1. Q_y(0)=0, M_x(l)=0, ____________________________________

2. M_x(0)=-L, M_x(l)=0, ___________________________________

3. M_x(0)=L, M_x(l)=0, ____________________________________

1. Q_y(0)=0, M_x(l)=-L, ____________________________________

2. M_x(l)=-L, M_x(0)=0, ____________________________________

3. M_x(0)=L, M_x(0)=0, ____________________________________

1. Q_y(0)=P, M_x(l)=L, ____________________________________

2. M_x(0)=0, M_x(l)=L, ____________________________________

3. Q_y(0)=-P, M_x(0)=0, ___________________________________

- Чему равняется поперечная сила (в кН) в сечении А?

Рис

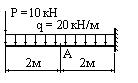
- Чему равняется изгибающий момент (в кНм) в сечении А?

Рис

- На каком расстоянии (в метрах ) от левой опоры А изгибающий момент максимальный?

Рис

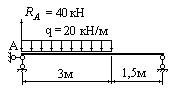
- Чему равняется максимальный изгибающий момент (в кНм), возникающий в балке?

Рис

- Во сколько раз изгибающий момент в защемлении (сечение А) больше, чем посредине консоли (сечение В)?

Рис

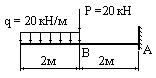
- Дана эпюра поперечных сил. Чему равна внешняя сила (в кН), приложенная в сечении В?

Рис

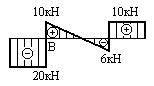
- Дана эпюра изгибающих моментов. Чему равен момент пары сил (в кНм), приложенной в сечении В ?

Рис

- Построить с помощью метода “характерных” сечений эпюру изгибающих моментов и определить величину максимального изгибающего момента M_max (кНм).

Рис

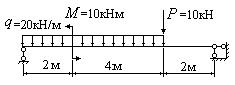
- Построить с помощью метода “характерных” сечений эпюру поперечных сил и определить величину максимальной поперечной силы (кН).

Рис

- Построить с помощью метода “характерных” сечений эпюру поперечных сил и определить величину поперечной силы в сечении С.

Рис

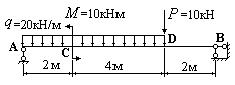
- Построить с помощью метода “характерных” сечений эпюру изгибающих моментов и определить величину изгибающего момента в сечении D.

Рис

- Определить нормальное напряжение (в МПа) при изгибе балки в точке А поперечного сечения, удаленной от нейтральной линии сечения на 2 см, если изгибающий момент M=0,18 кНм.

Рис

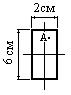
- Определить величину касательных напряжений (в МПа) при изгибе в точке А поперечного сечения, если поперечная сила Q=40 кН.

Рис

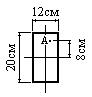
- У которой из фигур, имеющих одинаковую площадь, момент сопротивления относительно оси z, будет наибольшим? Определить наибольший момент сопротивления.

Рис

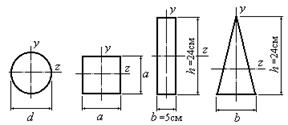
Онлайн-калькулятор "Расчет прочности при изгибе"

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00

Главная

Общие сведения

Механические испытания на изгиб

Построение эпюр поперечной силы и изгибающего момента

Основные дифференциальные соотношения теории изгиба

Примеры построения эпюр внутренних силовых факторов для консольных балок

Примеры построения эпюр внутренних силовых факторов для балок на двух опорах

Другие подходы к построению эпюр внутренних силовых факторов

Напряжение при чистом изгибе

Энергия упругих деформаций балки

Касательные напряжения при поперечном изгибе. Главные напряжения при изгибе

Рациональные формы поперечных сечений при изгибе

Полная проверка прочности. Опасные сечения и опасные точки

Перемещения при изгибе балок. Дифференциальное уравнение изогнутой оси упругой балки

Пределы применимости приближенной теории из­гиба балок

Общие дифференциальные соотношения при изгибе

Интегрирование дифференциального уравнения изогнутой оси балки методом начальных пара­метров

Простейшие статически неопределимые задачи при изгибе. Метод сравнения (наложения) пере­мещений

Расчет на прочность простейших статически неопределимых балок методом допускаемых нагрузок

Изгиб балок переменного поперечного сечения

Балка равного сопротивления

Балка на упругом основании

Изгиб составных балок

Вопросы для самопроверки

Пределы применимости приближенной теории изгиба балок

Интегрирование дифференциального уравнения изогнутой оси балки методом начальных параметров

Простейшие статически неопределимые задачи при изгибе. Метод сравнения (наложения) перемещений