Главная

Лекция 6 (продолжение). Примеры решения на плоский изгиб

 

Определение перемещений и проверка жесткости балок при изгибе

При расчете строительных и машиностроительных конструкций на жесткость (в большинстве случаев по прогибам, по углам поворота) должно соблюдаться условие

                                          

т.е. относительный прогиб f/l, подсчитанный при действии нормативных нагрузок, не должен превышать установленный нормами предельный прогиб 1/n_o  для данного вида конструкции.

Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости – ограничение угла поворота  опорных сечений:

.                                       

Допускаемый угол поворота  берется из соответствующих справочников. В среднем составляет 0,001 рад.

 

Пример 1.

Для консольной балки с сосредоточенной парой M_o на свободном конце найти аналитические выражения для прогибов и углов поворота.

 

Решение.

По дифференциальным уравнениям имеем

.

В заделке прогиб y(0) и угол поворота сечения  равны нулю. Эти граничные условия будут удовлетворены, если C₁=0 и C₂=0. Следовательно, балка изогнется по дуге параболы:

.

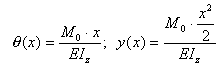На этом примере наглядно проявляется приближенный характер уравнения, так как при постоянном изгибающем моменте согласно равенству

балка должна изгибаться по дуге окружности радиуса . Однако в пределах длины балки указанные дуги окружности и параболы практически совпадают.

 

Пример 2.

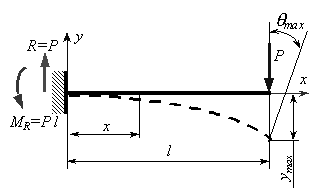
Для консольной балки с сосредоточенной силой P на свободном конце найти аналитические выражения для прогибов и углов поворота.

Решение.

Реактивная сила и момент в заделке равны R=P, M_R=Pl. В произвольном сечении на расстоянии x от заделки имеем

.

В заделке прогиб y(0) и угол поворота сечения  равны нулю. Эти граничные условия будут удовлетворены, если C₁=0 и C₂=0. Окончательно, имеем

.

Максимальные прогиб и угол поворота будут на правом свободном конце балки:

.

Знак минус в формулах для прогиба и угла поворота означает, что прогиб конца консольной балки направлен вниз, а поворот концевого сечения – по часовой стрелке.

 

Пример 3.

Для балки нагруженной распределенной нагрузкой найти аналитические выражения для прогибов и углов поворота.

 

Решение.

Изгибающий момент в произвольном поперечном сечении

.

В произвольном сечении на расстоянии x от опоры A имеем

.

Из условия для прогиба на левой опоре

.

Из условия для прогиба на правой опоре

.

Подставив значения C₁ и C₂ в уравнение, получим

.

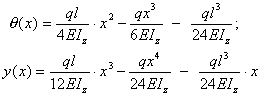На рисунке построены эпюры прогибов и углов поворота, из которых видно, что максимальный прогиб будет в середине балки

.

Максимальные углы поворота будут в опорных сечениях:

.

 

Пример 4.

Однопролетная шарнирно опертая балка находится под действием равномерно распределенной нагрузки (см. рис.).

Вывести дифференциальное уравнение изгиба и найти максимальные прогибы и углы поворота.

                                 а)                                                                                      б)

                                                            

Решение.

Опорные реакции в этой задаче  Перерезывающая сила и изгибающий момент, согласно методу сечений, равны:

                (1)

Строим для наглядности эпюры   (рис. а).

Подставляя найденное выражение для  в дифференциальные урав­нения изогнутой оси балки, получим:

                                                                        (2)

Интегрируя (2) дважды, находим:

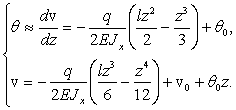                                                (3)

На краях балки при  имеем . Поэтому из (3) следует:

                                                                        (4)

Подставляя полученные значения  в (3), находим:

                                                   (5)

Максимальный прогиб имеет место в середине пролета при  и равен:

                                                                   (6)

Прогиб положителен, т.е. направлен вниз по оси у. Угол поворота. Геометрический смысл первой производной состоит в том, что она равна тангенсу угла наклона касательной в точке изогнутой оси с координатой z. На рис. б показано, в каких четвертях тангенс положителен и отрицателен, а также изображены фраг­менты касательных к изогнутой оси, отвечающие положительным и отрицательным углам поворота сечений

Перевернутая эпюра на рис. а построена на растянутых волокнах балки. Она напоминает изогнутую ось балки.

 

Пример 5.

1) Консольная балка изгибается силой Р на конце (см. рис. а).

2) Консольная балка изгибается распределенной нагрузкой (рис. б).

3) Консольная балка изгибается моментом на конце (рис. в).

Для всех трех балок найти дифференциальное уравнение изгиба и найти максимальные прогибы и углы поворота.

                                            а)                                                                 б)                                                  в)

 

Решение.

1) Из рис. а находим методом сечений:

                                       (1)

Дифференциальное уравнение изгиба

                                                    (2)

 Интегрируя, находим:

                           (3)

При z = 0 имеем граничные условия:

                                  (4)

Следовательно,

          (5)

Максимальный прогиб и угол поворота имеют место на конце консоли при z = , т.е.

                                      (6)

 

2) Из рис. б методом сечений находим:

                        (1)

Дифференциальное уравнение изгиба:

                                         (2)

Интегрируя, получаем:

           (3)

В защемлении балки при z=0 имеем  Максимальные угол поворота и прогиб имеют место на конце консоли при  т.е.

                                             (4)

3) В этом случае  

Дифференциальное уравнение изгиба:

                                                                              (1)

Интегрируя, получаем:

                  (2)

Так как прито получаем  Следовательно,

                                                 (3)

 

Пример 6.

1) Изгиб однопролетной балки моментом в опоре (рис. а).

2) Чистый изгиб однопролетной балки моментами m (рис. б).

Для обеих балок найти дифференциальное уравнение изгиба и найти максимальные прогибы и углы поворота.

                                    а)                                                                          б)                       

 

Решение.

1) Перерезывающая сила и изгибающий момент в произвольном сечении z равны:

                                                          (1)

Дифференциальное уравнение изгиба:

                                                                                                   (2)

откуда после интегрирования получаем:

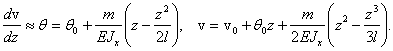              (3)

Из граничных условий v = 0 при z = 0 и z =  получаем:

                                                                                                    (4)

Следовательно,                (5)

Угол поворота на правой опоре:

                                                                                                                     (6)

2) В этом случае  Дифференциальное уравнение изгиба:

                                                                                              (1)

откуда после интегрирования:

                                  (2)

Из граничных условий  при  находим

Следовательно,

                                  (3)

Максимальный прогиб в середине пролета:

                                                                           (4)

 

Пример 7.

Определить вертикальное перемещение среднего и угол поворота торцевого сечения консольной балки.

 

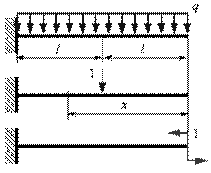
Решение.

Изгибающий момент от заданной нагрузки в текущем сечении M_z(x)= – qx²/2.

При нагружении единичной силой в среднем сечении балка будет иметь два, участка, причем на первом M_z¹(x)=0, а на втором M_z¹(x)= – 1 (x-l). Искомый прогиб в середине балки

.

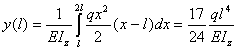Для определения угла поворота торцевого сечения приложим в этом сечении единичный момент. Тогда M_z¹(x)=1, искомый угол поворота торца балки

.

Следовательно, торцевое сечение поворачивается не в направлении вращения единичной пары (см. рис.), а в противоположную сторону - по часовой стрелке.

 

Пример 8.

Подобрать номер стального двутавра исходя из условий прочности и жесткости, если допускаемое напряжение =160 МПа, допускаемый   прогиб [f] = l / 400,  F = 50 кН, модуль упругости  Е = 200 ГПа.

 

Решение.

1. Подбор сечения по условию прочности. Максимальный изгибающий момент возникает в защемлении и равен  M_max = Fl = 50 кНм. По условию прочности   или  ,  откуда  

 = 50/(160) = 312,5 см³.

Принимаем двутавр № 24а, у которого W_x = 317 см³.

2. Подбор сечения по условию жесткости.

Максимальный  прогиб f = Fl³/(3EI_x).

По условию жесткости   или  ,  откуда

I_x = 400Fl²/(3E) = 400/(3) = 3333 см⁴.

Берем профиль № 24, для которого I_x = 3460 cм⁴.

Окончательно принимаем двутавр № 24а, удовлетворяющий как условию прочности, так и жесткости.

 

Пример 9.

Подобрать диаметр деревянной балки круглого сечения, удовлетворяющей условиям прочности и жесткости, если q =1 кН/м,  а =1 м,  = 10 МПа,  = 1 МПа,   Е = 10 ГПа,    [f] = l/400.

Решение.

1. Построение эпюр Q и М_х. Опорные реакции:

R_A = R_B = 2qa.

Расчетные внутренние факторы:

Q_max = 2qa = 2кН,    M_max = 4qa² = 4 кНм.

2. Подбор сечения из условий прочности:

по нормальным напряжениям

,    W_x=d³/32, 

по касательным напряжениям

 ,    A=(/4)d²,  откуда

 .

Таким образом, по условию прочности требуемый диаметр равен   .

3. Подбор сечения по условию жесткости. Определяем наибольший прогиб. Начало координат выбираем в середине балки (сеч. С). Тогда в силу симметрии = 0. Кроме того,  Q_o = 0  и  М_о = 4qa². Из условия опирания балки V_B = 0 или

.

Отсюда .

По условию жесткости , ,  откуда

Окончательно принимаем больший размер, т.е.

.

 

Пример 10.

На стальную двутавровую балку действует равномерно распределенная нагрузка. Определить интенсивность нагрузки q, если измерением установлено, что касательная к оси изогнутой балки на свободном конце составляет с осью Oz угол  = 8 мрад. Принять Е = 200 ГПа.

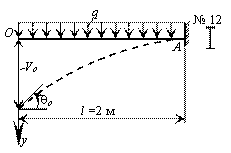
Решение.

Из условия опирания балки = 0 или  = + (1/EI_x)(ql³/6) = 0, из которого находим

 = -ql³/(6EI_x).   Отсюда

q = 6EI_x/l³ = 6/2³ = 4,2 кН/м.

 

Пример 11.

Дюралевая круглая труба сечением 50х44 мм положена горизонтально на две опоры. Определить максимальный допускаемый пролет l, исходя  из  условий  прочности  и жесткости, если  [f] = l/200,   = 115 МПа,    = 26 кН/м³,  Е = 75 ГПа.

Решение.

1. Расчет на прочность. Геометрические характеристики сечения

;

;

  .

Погонная нагрузка    .

Из условия прочности      или

,   откуда

.

2. Расчет на жесткость. Наибольший прогиб в данном случае равен .

Из условия жесткости ,   откуда

Окончательно принимаем меньшую из двух найденных величин, т.е.   .

 

Пример 12.

При загружении сосновой доски, свободно лежащей на двух опорах, силой F = 24 Н посредине был измерен прогиб под силой  f = 5  мм. Определить модуль упругости материала.

 

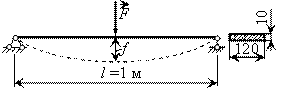
Решение.

Как известно, прогиб под силой равен , откуда   .

Вычисляем момент инерции

 и находим 

.

 

Пример 13.

Определить прогиб балки, изображенной на рисунке. Жесткость балки на изгиб – EI.

 

Решение.

Определяем опорные реакции R_A и R_B:   тогда R_A = R_B = m/l.

Балка состоит из одного участка. Составляем уравнение упругой оси балки:

а затем его интегрируем: 

    (1)

Для определения постоянных интегрирования С и D поставим граничные условия: при х = 0 имеем у = 0 и при х = l также имеем у = 0, т.е. получаем  у(х = 0) = D = 0, откуда D = 0, далее

,

откуда находим С = –ml/(3EI).

Подставляя полученное значение С в формулы (1), окончательно запишем результаты:

 

 

Пример 14.

Провести расчет по второй группе предельных состояний (по прогибам) главной двутавровой балки рабочей площадки производственного здания при отсутствии рельсовых путей (см. рис.). Нормативная нагрузка q = 8 кН/м, длина консоли l = 2 м.

 

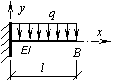
Решение.

Максимальный прогиб  будет на конце консоли в точке В:

С учетом примечания к табл. 1 принимаем  [1/n_o] = 1/400 и формулу  можно записать в следующем виде

 

Таблица 1. Предельные относительные прогибы  изгибаемых элементов

металлических конструкций

                                                                              Примечание: Для консолей пролет l равен удвоенному вылету консоли.

или 

Из полученного соотношения определяем

По сортаменту прокатных профилей «Двутавры стальные горячекатанные» принимаем двутавр № 16 (I_z = 873 см⁴, W_z = 109 см³).

Проверим прочность балки из двутавра № 16. Согласно рисунку, имеем  M_max = ql²/2 =16000 Нм и тогда находим для стали С255:

По сортаменту прокатных профилей «Двутавры стальные горячекатанные» принимаем двутавр № 14 с W_z = 81,7 см³, I_z = 572 см⁴.

Следовательно, согласно расчету на прочность можно использовать в качестве балки рабочей площадки двутавр № 14. Однако в этом случае конструкция будет непригодна к нормальной эксплуатации из-за появления недопустимых перемещений (прогибов). Окончательно принимаем двутавр № 16, который необходим из расчета на жесткость.

 

Пример 15.

Подобрать из расчета на прочность главную балку междуэтажного перекрытия двутаврового поперечного сечения и проверить условие жесткости для нее (см. рис.). Принять F = 30 кН, l = 6 м. Материал балки – сталь С255, = 1,1.

Решение.

Определяем опорные реакции в рассматриваемой однопролетной балке R_A = R_B = F = 30 кН. Максимальный изгибающий момент будет в середине пролета:

М_max = R_Al/2 – F(l/2 – l/3) = 60 кНм,

следовательно, согласно условия:

По сортаменту прокатных профилей «Двутавры стальные горячекатанные» принимаем двутавр № 22 ( W_z = 232 см³, I_z = 2550 см⁴).

Максимальный прогиб будет также в середине пролета балки. Составим дифференциальное уравнение изгиба оси балки для первого участка:

  

Поставим граничное условие:  y_I = 0 при х = 0 и находим D = 0. Далее запишем

 

при  а также для третьего участка ():

Граничное условие для третьего участка примет вид: y_III = 0 при х = 6м, откуда найдем С = –120/(EI).

Максимальный прогиб будет в середине пролета балки на втором участке при х = 3 м:

Для принятого по расчету двутавра № 22 выписываем I = 2550 см⁴. В этом случае условие жесткости  принимает вид

Таким образом, главная балка междуэтажного перекрытия из двутавра № 22 будет непригодна к нормальной эксплуатации, вследствие появления недопустимо больших прогибов.

Проведем расчет на жесткость. Формулу  представим в виде

  откуда 

где принято

Окончательно принимаем из условия проверки жесткости балки двутавр № 33 (I_z = 9840 см⁴, W_z = 597 см³).

Максимальное нормальное напряжение в этом случае будет

 

Пример 16.

На балку моносимметричного сечения, выполненную из чугуна, действует нагрузка, показанная на рис. 1, а. Поперечное сечение балки изображает рис. 2. Надо найти грузоподъемность балки, т.е. значение допускаемой нагрузки, при которой обеспечены прочность и жесткость балки. Допускаемое значение максимального прогиба балки задано.

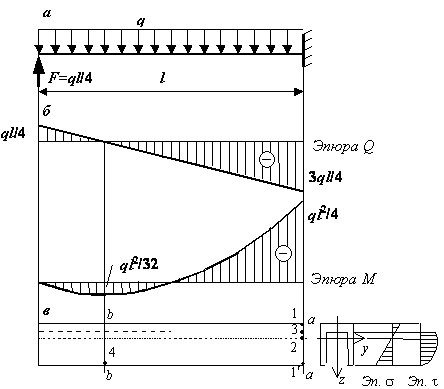
                                                                         Рис.1

 

Решение.

Найдем геометрические характеристики заданного поперечного сечения: осевые моменты инерции относительно главных центральных осей. Сечение имеет только одну ось симметрии, эта ось является одной из главных осей инерции. Обозначим ее z. Вторая главная ось y проходит через центр тяжести сечения. Определим положение центра тяжести сечения по формуле

.

                                     Рис.2

 

Статический момент определяем относительно произвольной оси а–а, перпендикулярной оси z (оси симметрии), как сумму статических моментов фигур, составляющих заданное поперечное сечение. В данном случае сечение разбиваем на три прямоугольника и площадь сечения состоит из площадей трех фигур: двух стенок А_с и полки А_п: . Ось а–а рационально расположить так, чтобы статический момент одной из фигур равнялся нулю. Это произойдет, если ось а–а провести через центр тяжести какой-то фигуры, например, через центр тяжести полки (см. рис. 2).

Тогда статический момент полки равен нулю и полный статический момент S_a равен удвоенному статическому моменту стенки:

.

Здесь первый множитель – удвоенная площадь стенки, второй – координата центра тяжести стенки (При вычислении статического момента не забывайте учитывать знаки координат центра тяжести).

Найдя положение центра тяжести сечения, проведем через него вторую главную ось y (см. рис. 2). Рекомендуем рисовать сечение в масштабе, тогда по масштабу можно проконтролировать правильность определения центра тяжести сечения. В данном случае очевидно, что центр тяжести должен быть смещен к полке.

Теперь определим осевой момент инерции относительно оси y. Находим его как сумму моментов инерции трех фигур: двух стенок () и полки (). Для определения момента инерции каждой фигуры используем формулу

.

Здесь  – момент инерции фигуры относительно оси y₀, проходящей через центр тяжести фигуры и параллельной оси y, а – расстояние между осями y и y₀. Таким образом,

.

Расстояния h₁ и h₂ показаны на рис. 2. Моменты инерции полки и стенки относительно собственных осей y₀  находим по формуле, справедливой для прямоугольника,

,

где b – ширина прямоугольника (параллельна оси y₀); h – его высота. Например, для полки

.

Примечание. Рекомендуем для тренировки аналогично найти момент инерции поперечного сечения относительно оси z, несмотря на то, что в проверке прочности этой балки он не участвует.

Строим эпюры поперечной силы и изгибающего момента, выражая ординаты через неизвестный параметр нагрузки (в данной задаче через q – см. рис. 1, б).

Прежде чем находить положение опасных сечений и опасных точек по эпюрам Q и М, выясним как рационально расположить поперечное сечение балки: полкой вверх или полкой вниз. Поскольку чугун – хрупкий материал и прочность при растяжении у него меньше прочности  при сжатии, оптимальным положением сечения является такое положение, при котором максимальные растягивающие напряжения будут меньше максимальных по модулю сжимающих напряжений. В рассматриваемом примере максимальный изгибающий момент отрицателен, то есть балка в сечении, где действует , изгибается выпуклостью вверх и растягивающие напряжения будут в верхних волокнах. Поэтому располагаем поперечное сечение так, чтобы центр тяжести сечения был ближе к верхним волокнам, т. е. полкой вверх.

Найдем положение опасных сечений и опасных точек так же, как в двутавровой балке (см. рис. 1, в). Поскольку максимальная поперечная сила и наибольший изгибающий момент действуют в данном примере в одном сечении, то опасные точки 1, 1¢,  2 и 3 расположены в одном сечении а–а. Особенностью расчета балок из хрупкого материала является то обстоятельство, что точки 1 и 1¢ не являются равноопасными. Так как хрупкий материал имеет разную прочность при растяжении и сжатии, то проверять прочность надо как в точке 1, в которой действуют  максимальные растягивающие напряжения, так и в точке 1¢ с наибольшими сжимающими напряжениями. Если эпюра изгибающих моментов меняет свой знак, как в рассматриваемом примере, то появляется еще одна опасная точка – точка 4 (см. рис. 1, в). В этой точке действуют растягивающие напряжения, и  поскольку она расположена дальше от нейтральной оси, чем точка 1, величина растягивающего напряжения в точке 4 может оказаться больше, чем в точке 1 несмотря на то, что изгибающий момент в сечении b–b меньше, чем в сечении а–а.

Определим допускаемую нагрузку из условия прочности в точке 1, где действуют максимальные растягивающие напряжения:

,

откуда

.

Здесь 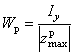 – момент сопротивления растяжению; – расстояние до наиболее растянутого волокна показано на рис. 2.  Для рассматриваемого примера  и  .

Проверим прочность в остальных опасных точках, используя найденное значение допускаемой нагрузки. В точке 1¢ с наибольшими сжимающими напряжениями

,

где  – момент сопротивления сжатию. (Расстояние  показано  на рис. 2.)

Для рассматриваемого примера опасной является и точка 4. Условие прочности в этой точке:

.

Чтобы проверить прочность в точке 2 с максимальными касательными напряжениями, находящейся в напряженном состоянии "чистый сдвиг", необходимо применить теорию прочности, справедливую для хрупкого материала. Например, из теории Мора  для чистого сдвига получим следующее условие прочности:

,

где максимальное касательное напряжение определяем по формуле Журавского 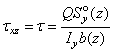, в которой статический момент  находим для отсеченной части, расположенной по одну (любую) сторону от нейтральной оси.

 Наконец, условие прочности в точке 3, где действуют и нормальные (растягивающие), и касательные напряжения, записываем по теории прочности для "балочного" напряженного состояния, справедливой для хрупкого материала, например по теории Мора . Нормальные и касательные напряжения в этой точке определяем по формулам   и .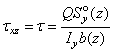

Если в какой-то точке условие прочности не будет выполняться, необходимо найти новое значение допускаемой нагрузки из условия прочности в этой точке.

В рассматриваемой задаче, кроме условия прочности, должно выполняться и условие жесткости, т. е. максимальный прогиб не должен превосходить значения допускаемого прогиба. Вопрос о нахождении прогибов решается в разделе "Определение перемещений и проверка жесткости балок".

 

Пример 17.

Для балки, изображенной на рис. а, требуется:

1) построить эпюры Q и M;

2) подобрать сечение двутавр =160 МПа;

3) построить изогнутую ось балки аналитическим методом вычислив прогибы в характерных сечениях и в середине пролета ;

4) проверить жесткость при [V]=l/500, если: Р=34 кН, m=14 кНм, q=18 кН/м, l=5,6 м.

Решение.

1. Определение опорных реакций:

Проверка:

2. Построение эпюр Q и М

Эпюры Q и М строим методом характерных сечений.

Эпюра Q (рис. б):

Эпюра М (рис. в):

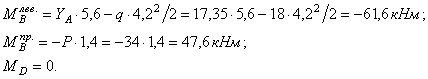
3. Подбор сечения

По ГОСТ 8239—89 подбираем двутавр №30, W_x=472 см³, J_x=7080 см⁴.

Жесткость поперечного сечения:

ЕJ_x=2×10⁵×10⁶×7080×10^-8=14160×10³ Нм².

4. Построение изогнутой оси:

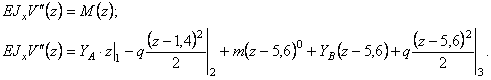
Дважды интегрируем:

Определяем постоянные интегрирования:

при z=0, V(0)=0, следовательно D=0;

при z=5,6 м, V(5,6) =0,

 отсюда С= -49,01 кНм².

Определяем прогиб в сечении С, z =1,4 м — подставляем в уравнение прогибов:

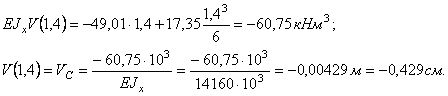
Определяем прогиб в сечении К, z =2,8 м — подставляем в уравнение прогибов:

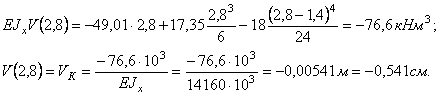
Определяем прогиб в сечении D, z =7 м — подставляем в уравнение прогибов:

По вычисленным значениям прогибов строим изогнутую ось балки (рис. г). Положительные прогибы откладываем вверх (по направлению оси V), отрицательные прогибы откладываем вниз.

 

Пример 18.

Требуется:

Для схемы «а»:

1. Построить эпюры поперечной силы Q и изгибающего момента M.

2. Проверить прочность  по нормальным напряжениям в балке сложного поперечного сечения, уже рассмотренного в задаче 3.

3. Вычислить коэффициент использования прочности стали балки.

4. Определить прогиб конца консоли аналитическим методом, составляя и интегрируя дифференциальные уравнения изогнутой оси балки.

Для схемы «б»:

1. Построить эпюры поперечной силы Q и изгибающего момента M.

2. Подобрать сечения следующей формы: прямоугольное (h/b= k); круглое; кольцевое (); состоящее из двух швеллеров; двутавровое.

3. Оценить эффективность формы сечения.  

Для всех вариантов принять расчетное сопротивление стали R =240 МПа, модуль упругости (модуль Юнга)  МПа.

Исходные данные для «а».

, , , , R =200 МПа.

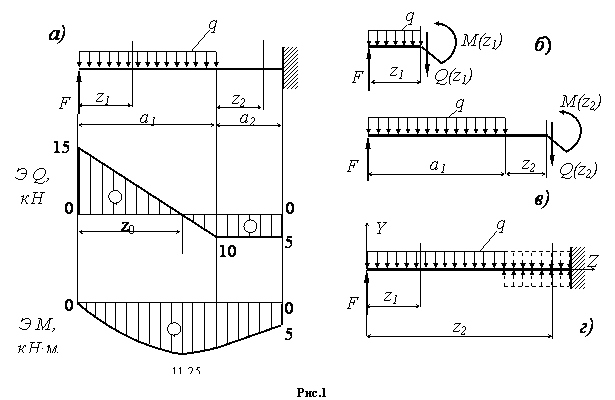
Решение.

1. Построим эпюры поперечных  сил Q и изгибающих моментов M.

- Получим выражения для Q и M по участкам. Заданная балка имеет два участка нагружения: по длине первого участка распределена равномерная нагрузка q, прекращение действия которой означает начало второго участка (см. рисунок 1, а). На рисунке z₁ и z₂ - координаты поперечных сечений первого и второго участков. Для каждого участка выбирается своя система координат.

I –й участок: 

Рассматривая равновесие левой отсечённой части балки (см. рисунок 1, б), запишем выражения для  и

.                                                                                       (1)

                                                                       (2)

Выражение (1) представляет собой уравнение наклонной прямой. Для её построения достаточно вычислить поперечную силу в двух точках:

в начале участка при  ;

в конце участка при   .

Отметим, что на рассматриваемом участке поперечная сила меняет знак, пересекая ось эпюры. Согласно дифференциальной зависимости между  Q и M  в сечении, где =0,  изгибающий момент принимает экстремальное значение.

Определим координату интересующего нас сечения. 

При

Эпюра изгибающих моментов M  представляет квадратную параболу (выражение (2)), для её построения подсчитаем координаты M в трёх точках:

;

;

z₁==1,5 м     .

II –й участок:                         

Рассматривая равновесие левой части, отсечённой сечением с координатой  (см. рисунок 1, в), запишем выражения для  и .

.

Полученное выражение представляет собой уравнение прямой, параллельной оси эпюры.

.

В данном случае мы получили уравнение прямой, наклонной к оси эпюры. Для её построения определим координаты двух крайних точек.

;

- Строим эпюры Q и M. Результат представлен на рис. 1, а.

2. Проверка прочности балки проводится по поперечному сечению, где изгибающий момент на эпюре достигает наибольшего значения независимо от знака.

Для этого следует воспользоваться формулой:

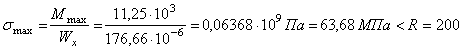МПа,

следовательно, прочность обеспечена. 

3. Определяем коэффициент использования прочности стали

.

Коэффициент использования  прочности составляет около 32%. В хорошо подобранных сечениях перенапряжение или недонапряжение не превышает .

4. Определяем прогиб конца консоли аналитическим методом

- Составляем приближённые дифференциальные уравнения изогнутой оси балки по участкам с соблюдением условий Клебша.

Необходимо отметить, что в этом случае выбирается только одна система координат с началом в крайней левой точке балки (см. рис.1, г). Если в этой точке балка жёстко или шарнирно зафиксирована, то прежде чем приступить к составлению уравнений, необходимо определить реакции в опорах.

Для нашего случая:

I –й  участок:  ,                                                             

  ;

II –й участок:    ,      .

- Дважды интегрируем дифференциальные уравнения

- Рассматриваем граничные условия и доказываем равенство постоянных интегрирования на обоих участках

При  (на границе двух смежных участков балки) , , так как они являются углами поворота и прогибами, соответственно, одного и того же сечения.

Тогда, учитывая формулы (2) и (4), получим:

,   откуда   .

Приравнивая прогибы, из выражений (3) и (5) имеем:

, откуда   .

Следовательно, приём Клебша сводит решение задачи к вычислению только двух постоянных интегрирования C, D.

- Из начальных условий определяем значения постоянных интегрирования C и D

Первое условие:   при , , в защемленном конце балки угол поворота  равен нулю. Тогда, согласно уравнению (5):

.

Откуда  .

Второе условие:   при ,   , так как в заделке балки прогиб равен нулю. Из выражения (6) найдем вторую постоянную интегрирования

.

Откуда   .

- Вычисляем прогиб конца консоли

Для этого воспользуемся формулой (4), при :

.

Согласно принятому направлению координатных осей (см. рис. 1, г), при решении задачи аналитическим методом знак «+» указывает на то, что прогиб конца консоли балки направлен вверх.

Исходные данные для «б».

, , , , R = 160 МПа.

                                                Рис.2

Решение.

1. Построим эпюры  Q и  M.

- Определяем опорные реакции балки. Заданная балка зафиксирована в двух сечениях с помощью шарнирно-подвижной и шарнирно-неподвижной опор  (см. рис. 2). Характер прикладываемой нагрузки обуславливает необходимость определения только вертикальных реакций опор  и , так как горизонтальная составляющая реакции в опоре А равна нулю ().

Проверка:   .

Полученное тождество свидетельствует о правильности результатов.

- Записываем уравнения для Q и M по участкам. Для каждого участка выбирается своя система координат

I –й участок:     

Рассматриваем равновесие левой части балки

.

II –й участок:   

Рассматриваем равновесие правой части балки

.

.

.

При    ,

тогда     

- Строим эпюры Q и M. Результат представлен на рис. 2.

2. Подбор сечений указанных в задании форм.

Условие прочности при изгибе по нормальным напряжениям для пластичных материалов:

Отсюда требуемый момент сопротивления

При , предельное значение  момента сопротивления:

- Подбираем прямоугольное сечение. Соотношение сторон  (рис.3).

          Рис.3

 

Так как для прямоугольного сечения момент сопротивления относительно оси X  и по условию , то:

,

,

.

- Подбираем круглое сечение.

                    Рис.4

 

Для круглого сечения осевой момент сопротивления (рис. 4)  ; тогда

;

.

- Подбираем кольцевое сечение. Отношение диаметров   (рисунок 4).

                      Рис.5

 

Для кольцевого сечения осевой момент сопротивления  .

Тогда

;

;

.

- Подбираем сечение, состоящее из двух швеллеров.

             Рис.6

 

В основе определения осевого момента сопротивления лежит соотношение

С учётом того, что рассматриваемое сечение состоит из двух равных частей (рис. 6)

.

Требуемый момент сопротивления одного швеллера

.

По таблице ГОСТ 8240-89 выбираем швеллер №14 с ближайшим большим моментом сопротивления . Площадь сечения балки из двух швеллеров:

- Подбираем двутавровое сечение.

            Рис.7

 

Как и в предыдущих четырех случаях, момент сопротивления двутавра W_Х  (рис. 7)  должен быть не менее требуемого

По таблице ГОСТ 8239-89 принимаем двутавровую балку № 18 с ближайшим значением момента сопротивления, значение которого отвечает условию проектировочной задачи:

.

3. Оцениваем эффективность формы сечения.

Для чего сравниваем площади всех подобранных сечений.

Наиболее эффективной формой сечения балки (балка с наименьшим весом) является двутавровое сечение, наименее эффективной – круглое сплошное сечение.

 

Онлайн-калькулятор "Подбор кольцевого сечения балки при изгибе"

 

---