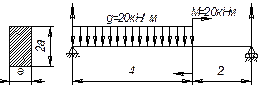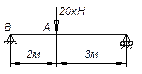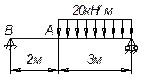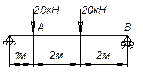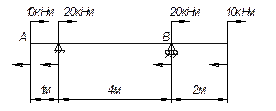Главная

Лекция 6 (продолжение). Задачи для самостоятельного решения

 

Содержание

Построение эпюр поперечной силы и изгибающего момента для балок

Определение напряжений и проверка прочности балок при плоском поперечном изгибе

Определение перемещений и проверка жесткости балок при изгибе

Расчет перемещений методом начальных параметров

 

Построение эпюр поперечной силы и изгибающего момента для балок

 

Задача 1.

Во сколько раз пролет балки l должен быть больше длины консоли а, чтобы изгибающие моменты в середине пролета и на провой опоре имели противоположные знаки и одинаковые значения. Построить эпюры Q и М.

Ответ:

 

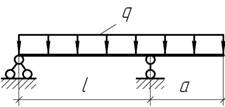
Задача 2.

Определить длину консоли а, если момент посередине пролета балки равен нулю. построить эпюры Q и М.

Ответ: а=2 м;

 

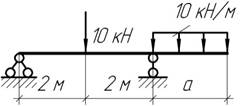
Задача 3.

Определить при каких значениях сил F изгибающий момент в опорном сечении консольной балки будет равен нулю. После этого построить эпюры Q и М_х.

Ответ: F=10 кН;

 

Задача 4.

По эпюрам поперечных сил Q и изгибающих моментов М установить нагрузку, действующую на балку.

 

Задача 5.

По заданной эпюре Q установить нагрузку, действующую на балку и построить эпюру М.

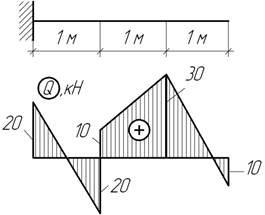
Ответ: М_max=-30 кНм

 

Задача 6.

По заданной эпюре М установить нагрузку, действующую на балку и построить эпюру Q.

Ответ: Q_max=16 кН

 

Задача 7.

Построить эпюру поперечных сил Q и изгибающих моментов М установить нагрузку, действующую на балку.

 

Задача 8.

По эпюрам поперечных сил Q и изгибающих моментов М установить нагрузку, действующую на балку.

 

Задача 9.

По заданной эпюре изгибающих моментов М установить нагрузку, действующую на балку и построить эпюру поперечных сил Q.

 

Задача 10.

По заданной эпюре Q установить нагрузку, действующую на балку и построить эпюру М.

 

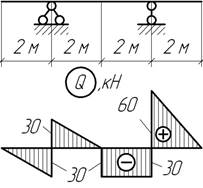
Ответ: М_max=-60 кНм

 

Задача 11.

Построить эпюры поперечных сил и изгибающего момента.

Ответ:

 

Задача 12.

Построить эпюры поперечных сил и изгибающего момента.

Ответ:

 

Задача 13.

Построить эпюры поперечных сил и изгибающего момента.

Ответ:

 

Задача 14.

Консоль длиной l=3а нагружена равномерно распределенной нагрузкой и сосредоточенной силой. Установить, при каком значении силы Р момент в заделке обратиться в нуль. Построить эпюры Q и М при найденном значении силы Р.

Ответ:

 

Задача 15.

Определить положение опоры С балки АВ при котором наибольшее по абсолютной величине отрицательный и положительный изгибающие моменты будут одинаковы (размер l  задан).

Ответ: а=0,536l, условия для определения а имеет вид

 

Задача 16.

По эпюрам поперечных сил Q и изгибающих моментов М установить нагрузку, действующую на балку.

 

Задача 17.

Консоль длиной l=3а нагружена равномерно распределенной нагрузкой и сосредоточенными силами. Установить, при каких значениях сил Р момент в заделке обратится в нуль. построить эпюры Q и М при найденных значениях сил Р.

Ответ:

 

Задача 18.

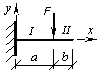
Найти направление и значение силы F, приложенной в сечении К консольной балки, если поперечная сила в заделке равна нулю. Построить эпюры Q и М_х.

Ответ:

 

Задача 19.

Найти длину консоли а из условия, что поперечная сила посредине пролета балки равна нулю. Построить эпюры Q и М_х.

Ответ:

 

Задача 20.

Консоль длиной l=3а нагружена равномерно распределенной нагрузкой и сосредоточенной силой. Установить, при каком значении силы Р момент в заделке обратится в нуль. Построить эпюры Q и М при найденном значении силы Р.

Ответ:

 

Задача 21.

Определить направление и значение сосредоточенного момента М приложенного в сечении К консольной балки, если изгибающий момент в заделке равен нулю. Построить эпюры Q и М_х.

Ответ: М=10 кНм (против часовой стрелки);

 

Задача 22.

По заданной эпюре М установить нагрузку, действующую на балку и построить эпюру Q.

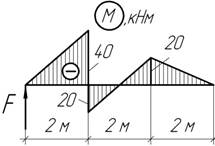
Ответ:

 

Задача 23.

Определить величину а, при которой экстремальные значения изгибающих моментов в балке АВ будут одинаковы.

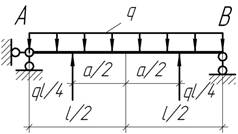
Ответ: a=l/4

 

Задача 24.

Консоль длиной l=3a нагружена равномерно распределенной нагрузкой и сосредоточенной силой. Установить при каком значении силы Р момент в заделке обратится в нуль. Построить эпюры Q и М при найденном значении силы Р.

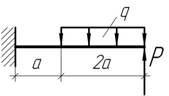
Ответ:

 

Задача 25.

Определить длину консоли а, если момент посредине пролета балки равен нулю. построить эпюры Q и М.

 

Задача 26.

Найти длину консоли а из условия, что поперечная сила посредине пролета балки равна нулю. Построить эпюры Q и М.

 

Задача 27.

По заданным эпюрам Q и М установите нагрузки действующие на балку.

 

Задача 28.

По заданным эпюрам изгибающего момента постройте эпюру Q и установите нагрузки, действующие на данные балки.

 

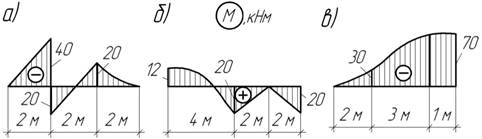
Задача 29.

По заданным эпюрам поперечной силы установите нагрузки, действующие на балки, и постройте эпюры изгибающего момента.

 

Задача 30.

Постройте эпюры Q_у и М_х для составных балок.

 

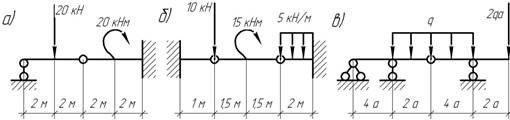
Задача 31.

Построить эпюры поперечных сил и изгибающего момента для простых балок.

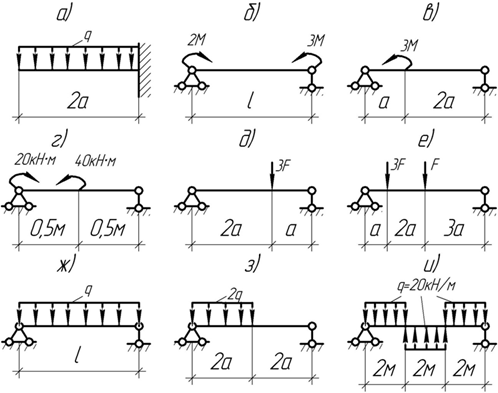
Ответ:

Схема	а	б	в	г	д	е	ж	з	и
Qmax	-2qa	M/l	M/a	20 кН	2F	3F		3qa
Mmax	2qa2	3M	-2M	30 кНм	2Fa	3Fa	ql2/8	9qa2/4

 

Задача 32.

Построить эпюры поперечных сил и изгибающего момента для балок с консолями.

Ответ:

Схема	а	б	в
Qmax	2F	-M/a	-qa
Mmax	-2Fa	2M	qa2

 

Задача 33.

Найти направление и значение силы F, приложенной в сечении К консольной балки, если поперечная сила в заделке равна нулю. Построить эпюры Q и М_х.

Ответ: F=20 кН (вверх); Q_max= - 40 кН; М_max=100 кНм.

 

Задача 34.

Определить, при каких значениях сил F изгибающий момент в опорном сечении консольной балки будет равен нулю. После этого построить эпюры Q и М_х.

Ответ: F=10 кН; Q_max= 10 кН; М_max= - 20 кНм.

 

Задача 35.

Определить направление и значение сосредоточенного момента М, приложенного в сечение К консольной балки, если изгибающий момент в заделке равен нулю. Построить эпюры Q и М_х.

Ответ: М=10 кНм ( против часовой стрелки); Q_max=10 кН; М_max= - 20 кНм.

 

Задача 36.

Найти длину консоли а из условия, что поперечная сила посредине пролета балки равна нулю. Построить эпюры Q и М_х.

Ответ: а=1 м; Q_max= - 20 кН; М_max= 15 кНм.

 

Задача 37.

Определить длину консоли а, если момент посредине пролета балки равен нулю. построить эпюры Q и М_х.

Ответ: а=2 м; Q_max= 20 кН; М_max= - 20 кНм.

 

Задача 38.

Во сколько раз пролет балки l должен быть больше длины консоли а, чтобы изгибающие моменты в середине пролета и на правой опоре имели противоположные знаки и одинаковые значения. Построить эпюры Q и М_х.

Ответ: l/a=2,45; Q_max= - 1,43qa; М_max= .

 

Задача 39.

Построить эпюры поперечной силы и изгибающего момента для балок, нагруженной треугольной (схема а, б, в) и распределенной моментной нагрузкой (схемы г, д, е).

Ответ:

Схема	а	б	в	г	д	е
Qmax	30 кН	-qa	1,5 qa	0	0	10 кН
Mmax	- 60 кНм		-3qa2		20 кНм	40 кНм

 

Задача 40.

Построить эпюры поперечной силы и изгибающего момента для составных балок.

Ответ:

Схема	а	б	в	г	д	е	ж	з	и
Qmax, кН	20	10	-40			-10	20	40
Мmax, кНм	-30	20	30	20	-10	-20		-60

 

Задача 41.

По заданным эпюрам Q и М_х установить нагрузку, действующую на балку.

Ответ: F₁=24 кН; F₃=5 кН – вверх; q₁₂=12 кН/м, F₂=5 кН – вниз; М₁=4 кНм; М₃=5 кНм; - против часовой стрелки.

 

Задача 42.

Построить эпюры Q и М_х для балки длиной l, шарнирно опертой по концам и нагруженной сплошной нагрузкой, изменяющейся по закону q=q₀sinkz, где k=2π/l.

Ответ:  

 

Задача 43.

По эпюрам Q и М_х определить нагрузку, действующую на балку.

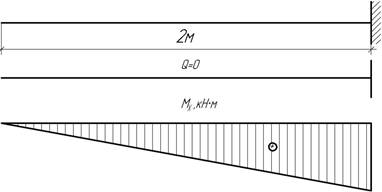
Ответ: m=10 кН/м.

 

Задача 44.

По заданной эпюре Q установить нагрузку, действующую на балку, и построить эпюру М_х.

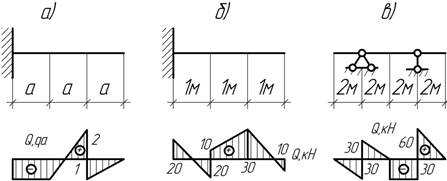
Ответ: а) М_max=qa²; б) М_max= - 30 кНм; в) М_max = – 60 кНм.

 

Задача 45.

По заданной эпюре М_х установить нагрузку, действующую на балку, построить эпюру Q. Криволинейный участок эпюры М_х очерчен по квадратной параболе. Кружком отмечена вершина параболы.

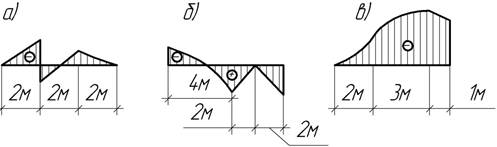
Ответ: а) Q_max= ; б) Q_max=16 кНм; в) Q_max=30 кНм

 

Задача 46.

Построить эпюры поперечных сил и изгибающих моментов для балок, защемленных одним концом и загруженных, как показано на рисунке. Подсчитать наибольшие по абсолютному значению величины поперечных сил и изгибающих моментов, если F =20 кН, q =20 кН/м, М₀ = 40 кН/м и l =2 м.

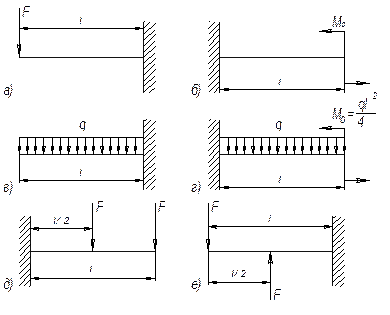
Ответ:

	а)	б)	в)	г)	д)	е)
Q, кН	20	0,0	40	40	40	20
M, кНм	40	40	40	20	60	20

 

Задача 47.

Построить эпюры поперечных сил и изгибающих моментов для балок на двух опорах, загруженных, как показано на рисунке. Найти тах Q и тах М при следующих данных: F= 60 кН, q =20 кН/м, М₀=60 кНм, l =3 м.

Ответ:

	а)	б)	в)	г)
Q, кН	30	30	20	40
M, кНм	45	22,5	60	60

 

Задача 48.

При каком значении силы F изгибающие моменты в опорных сечениях балок, изображенных на рисунке, будут равны нулю? Построить эпюры Q и М при этих значениях сил.

Ответ:

	а)	б)	в)	г)
F	ql/2	4qa/3	4qa/9	2qa/3

 

Задача 49.

Построить в общем виде эпюры Q_Y и M_X для заданной балки.

 

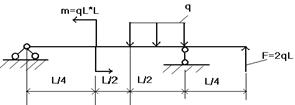
Задача 50.

Построить эпюры поперечных сил и изгибающих моментов, если L₁=0,2м; L₂=0,3м; q=4 кН/м.

    

 

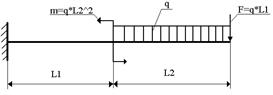
Задача 51.

Для изображенного стержня, определить внутренние усилия в сечениях А и В.

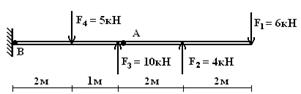
Ответ: в сечении А: Q_Y = 2 кН; N = Q_X = 0, M_X=-16 кНм; M_Z = M_Y = 0; в сечении В: Q_Y = -3 кН; N = Q_X = 0, M_X=-2 кНм; M_Z = M_Y = 0.

 

Задача 52.

Для всех стержней, изображенных ниже, определить вид деформации и построить эпюры соответствующих внутренних усилий. Для самоконтроля приведены уже построенные эпюры.

 

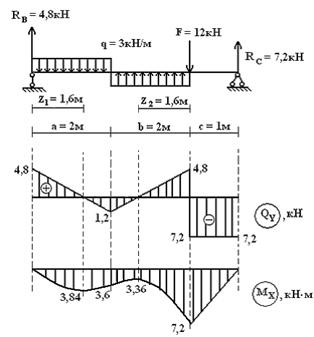
Определение напряжений и проверка прочности балок при плоском поперечном изгибе

 

Задача 1.

Вертикальный деревянный столб высотой 10 м должен работать с десятикратным запасом прочности при ветровой нагрузки р=1,25кН/м². Подобрать диаметр столба, если давление ветра на цилиндр можно считать равным 0,785 давления на площадь диаметрального сечения, а предел прочности материала на изгиб равен 42 МПа.

Ответ: d=35 см.

 

Задача 2.

Балка пролетом l=6 м спроектирована из брусьев квадратного сечения со стороной b=25 см. На стройке их заменили круглыми бревнами с такой же площадью поперечного сечения. Как изменится наибольшее нормальное напряжение в балке в результате такой замены? Какой следует выбрать диаметр бревен, чтобы обеспечить проектную прочность?

Ответ: увеличится на 18%; d=30 см.

 

Задача 3.

Кусок высокопрочной стальной проволоки длиной l=3,14 м упруго сгибается в окружность и концы сопрягаются плавно. Определить наибольший диаметр проволоки, при котором после изгиба в ней не возникает остаточных деформаций, если .

Ответ: d_max=2 мм.

 

Задача 4.

Чугунная труба с наружным диаметром d_н=20 см и толщиной стенки t=1 см наполнена водой и свободно опирается по концам. При каком расстоянии между опорами наибольшее напряжение в трубе будет равно 30 МПа, если  

Ответ: l=9,7 мм.

 

Задача 5.

Во сколько раз увеличится вес балки прямоугольного сечения при увеличении нагрузки в 4 раза? Вид нагрузки, пролет балки и допускаемое напряжение остаются неизменными. сечение балки изменяется только по высоте, а ширина остается постоянной.

 

Задача 6.

Балка прямоугольного сечения с соотношением сторон h/b=3 в одном случае нагружается в плоскости yz, а в другом – в плоскости xz. Чему равно отношение наибольших нормальных напряжений для этих двух случаев нагружения?

 

Задача 7.

Во сколько раз увеличится момент сопротивления прямоугольного сечения относительно горизонтальной центральной оси, если увеличить в 5 раз: а) высоту h; б) ширину b?

 

Задача 8.

По проекту балка должна состоять из двух швеллеров №20. В процессе производства работ было решено заменить их одной балкой двутаврового профиля. Определить необходимый номер двутавра и выяснить, какое из решений экономичнее.

Ответ: Двутавр №24а, который экономичнее двух швеллеров на 20%.

 

Задача 9.

Определить максимальное нормальное напряжение σ_x,max в консольной балке, заделанной одним концом, от действия собственного веса. Длина консоли l = 4 м. Балка представляет собой электросварную прямошовную трубу с D = 114 мм и толщиной стенки t = 5 мм.

Ответ: σ_x,max = 23,35 МПа от М_max =1050,56 Н·м.

 

Задача 10.

Балка двутаврового профиля проектируется на действие изгибающего момента М_о при поперечной силе Q_о. Для испытания конструкции изготовлена модель балки, геометрически подобная проектируемой, со всеми размерами, уменьшенными в n раз. Испытание модели производится уменьшенными нагрузками, причем изгибающий момент М_м и поперечная сила Q_м в модели в одинаковое число раз меньше, чем М_о и Q_о. Установить соотношение между наибольшими касательными напряжениями в оригинале  и модели , если наибольшие нормальные напряжения в обоих балках одинаковы.

Ответ:

 

Задача 11.

Рассмотреть однопролетную деревянную балку прямоугольного поперечного сечения b×h, загруженную равномерно распределенной нагрузкой q. Получить формулы для вычисления ширины балки b из условия прочности по нормальным напряжениям и из условия прочности по касательным напряжениям (по скалыванию).

Ответ: b = 3ql²/(4h²R_И) – по нормальным напряжениям;   b = 3ql/(4hR_ск) – по скалыванию.     

 

Задача 12.

Определить наибольшие напряжения изгиба в ремне толщиной t=5 мм, охватывающем шкив диаметром D=25 мм, если модуль упругости ремня равен Е=500 МПа.

Ответ:

 

Задача 13.

Во сколько раз уменьшится допускаемая нагрузка для балки прямоугольного сечения (схема а) при замене ее балками половинной высоты (схема б)? При какой общей высоте  (схема в) балка из двух не скрепленных между собой брусьев будет равнопрочна балке по схеме а?

Ответ: Уменьшится в 2 раза,

 

Задача 14.

Сравнить допускаемые нагрузки для двух вариантов расположения поперечного сечения чугунной балки, если  

Ответ: [F₂]/[F₁]=1,25.

 

Задача 15.

Швеллерная балка нагружена изгибающим моментом в вертикальной плоскости. Какова должна быть толщина t балки, чтобы напряжение в верхней и нижней частях сечения относились как 3:1?

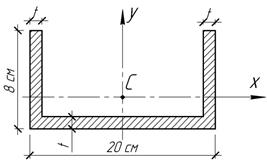
Ответ: t=6 мм.

 

Задача 16.

Определить диаметр бревна, из которого должен быть выпилен брус прямоугольного сечения bxh так, чтобы момент сопротивления его был наибольшим, если F=20 кН, [σ]=10 МПа, а=1,5 м.

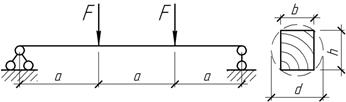
Ответ: d=36 см.

 

Задача 17.

Определить наивыгоднейшую по условию прочности балки длину а консоли. При найденном значении а подобрать сечение балки, если q=40 кН/м, l=6 м, [σ]=160 МПа. установить, так же во сколько раз вес данной балки меньше по сравнению с тем случаем, когда опоры расположены по его концам.

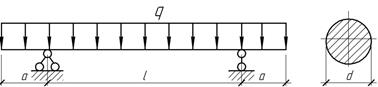
Ответ: а=2,12 м,  меньше в 3,24 раза.

 

Задача 18.

На сколько нужно срезать углы квадрата (рисунок а) и равностороннего треугольника (рисунок б), чтобы получить сечение, обеспечивающее максимальную прочность при изгибе? Оценить в процентах повышение грузоподъемности балок за счет подрезки сечений.

Ответ: Вариант а: α=1/9, грузоподъемность повышается на 5,3%. Вариант б: α=0,13, грузоподъемность повышается на 9,2%.

 

Задача 19.

Стальная балка круглого сплошного сечения диаметром d=100 мм выдерживает нагрузку F=5 кН. Со стороны свободного конца в ней делается отверстие диаметром  Определить наибольшую длину а ослабленной части балки, при которой ее несущая способность не изменится.

Ответ: а=1 м.

 

Задача 20.

Посредине деревянного бруса, плавающего на воде, приложена сосредоточенная сила F=1 кН. Определить наибольшие нормальные напряжения в брусе.

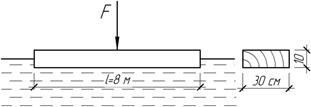
Ответ:

 

Задача 21.

Стальная балка сечением 6х10 см выдерживает нагрузку F=10 кН. На расстоянии 2,05 м от левой опоры требуется просверлить круглое отверстие. Определить наибольший диаметр отверстия, при котором грузоподъемность балки не меняется.

Ответ:

 

Задача 22.

Балка квадратного сечения нагружена силами F₁=12 кН и F₂=15 кН. Подобрать сечение балки, полагая [σ]=10 МПа. При эксплуатации этой балки в ней пришлось просверлить насквозь отверстие диаметром  Не опасно ли такое отверстие для прочности балки?

Ответ: b=20 см, отверстие не опасно, так как

 

Задача 23.

При испытании чугунной балки снимались показания тензометров Т₁ и Т₂. Средние приращения показаний от ступени нагружения ΔF=50 кН оказались равными  Определить момент инерции сечения относительно центральной оси х, если Е=120 ГПа, h=24 см, а=60 см, база тензометров s=20 мм, коэффициент увеличения 1000.

Ответ: I_х=6000 см⁴.

 

Задача 24.

Тензометр Т, установленный на стальной балке, имеет увеличение k=1000 и базу s=20 мм. Показания тензометра равно Δn=8 мм. Определить значение силы F и наибольшее напряжение в балке.

Ответ: F=10 кН,

 

Задача 25.

Деревянная платина сооружена из горизонтально сложенных досок 1, опирающихся на вертикальные стойки 2 квадратного сечения со стороной b=30 см, заделанные на нижнем конце и расположенные с шагом 1 м. Из условия прочности стоек определить максимально допустимый уровень оды, если [σ]=10 МПа.

Ответ: [Н]=3 м.

 

Задача 26.

Подземное помещение шириной 3 м перекрыто сплошным накатом из бревен диаметром d=20 см. Определить, на какой максимальной глубине Н под уровнем земли может быть заложено перекрытие, если [σ]=10 МПа и объемный вес грунта равен γ=17,5 кН/м³.

Ответ: Н_max=2 м.

 

Задача 27.

Подземная галерея, перекрытие которой находится на глубине Н=4 м от поверхности земли, имеет ширину l=3 м. Определить необходимый диаметр бревен сплошного настила, перекрывающего помещение, если [σ]=10 МПа, объемные вес грунта равен γ=20 кН/м³.

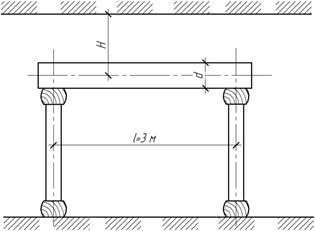
Ответ: d=30 см.

 

Задача 28.

Тензометр Т, установленный на стальной балке, имеет увеличение k=1000 и базу s=20 мм. Показания тензометра равно Δn=6 мм. Определить силу F, действующую на балку, а так же напряжения в точках С и Д.

Ответ: F=32 кН,

 

Задача 29.

Определить допускаемое значение силы F в двух вариантах: 1) все три бруса между собой склеены; 2) брусья между собой не скреплены. Принять а=1 м, b=24 см, h=5 см, [σ]=10 МПа, [τ]=1 МПа,  

Ответ:

 

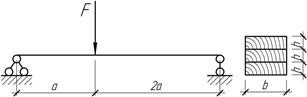
Задача 30.

Стальная балка изгибается по действием собственного веса. Найти абсолютное удлинение верхнего волокна mn, если наибольшее напряжение в балке равно 240 МПа.

Ответ:

 

Задача 31.

Тяжелый однородный стержень постоянного сечения используется как эталон длины. При какой длине консолей а длина стержня, измеренная по его верхней поверхности, не будет меняться в процессе деформации?

Ответ: а=0,211l.

 

Задача 32.

Определить из условия прочности балки АВ трубчатого сечения (d=20 см, α=0,84) допускаемое значение силы F, если [σ]=150 МПа. Балку СД не рассчитывать. Как изменится величина [F], если сила будет приложена непосредственно к балке АВ посредине ее пролета?

Ответ: [F]=80 кН, уменьшится в 2 раза.

 

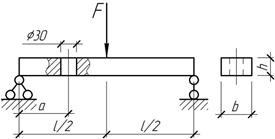
Задача 33.

Стальная балка, ослабленная сквозным отверстием, нагружена силой F=10 кН. Проверить прочность балки, полагая l=3 м, а=1 м, b=15 см, h=5 см,  Установить также наибольшее удаление отверстия от опоры , при которой прочность балки не нарушается.

Ответ:

 

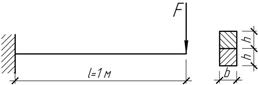
Задача 34.

Составная консоль склеена из двух балок. Определить допускаемую нагрузку F, если b=6 см, h=5 см, [σ]=60 МПа, предел прочности клея на сдвиг  нормативный запас прочности []=2. Соединение считать жестким.

Ответ: [F]=2 кН.

 

Задача 35.

Найти наибольшее нормальное напряжение в консольной балке и сравнить его с максимальным напряжением в заделке, если  При каких отношениях  наибольшее нормальное напряжение возникает в заделке?

Ответ:  при z=1 м,

 

Задача 36.

На суживающуюся консольную балку квадратного сечения действует сосредоточенная сила F=75 кН. Ширина и высота балки меняются по линейному закону от величины b на свободном конце до 2b в заделке. Определить максимальное нормальное напряжение, полагая b=10 см.

Ответ:  при  z=1,5 м.

 

Задача 37.

Консоль прямоугольного сечения постоянной ширины b=2,5 см и переменной высоты нагружена на свободном конце силой  и моментом  Определить наибольшее нормальное напряжение.

Ответ:  при  z=20 см.

 

Задача 38.

Определить соотношение частей изгибающего момента, воспринимаемого полками и стенкой двутавра при его изгибе.

Ответ: М_п/М_с=9,5.

 

Задача 39.

Два бруса квадратного сечения 10х10 см свободно уложены друг на друга и в загруженном состоянии по действием погонной нагрузки q=10 кН/м сварены по длине. Определить остаточные напряжения после снятия нагрузки, пренебрегая трением между брусьями.

Ответ:

 

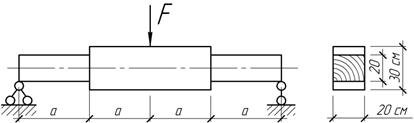
Задача 40.

Определить наибольшие нормальные и касательные напряжения, если F=40 кН, а=1 м.

Ответ:

 

Задача 41.

Во сколько раз уменьшится потенциальная энергия изгиба, если в балке сделать два узких симметричных надреза (схема 2). Силы F₁ и F₂ вызывают в балках наибольшие нормальные напряжения, равные пределу пропорциональности.

Ответ: В 2,44 раза.

 

Задача 42.

Балка прямоугольного сечения имеет переменный по высоте модуль упругости, изменяется по закону Е_у=Е(I+2|у|/h). Определить грузоподъемность балки при чистом изгибе, если  

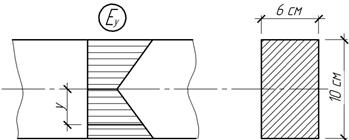
Ответ: [М]=7 кНм.

 

Задача 43.

Тонкая нерастяжимая лента толщиной t=2 мм наклеена на поверхность резинового бруса прямоугольного сечения 10х15 см. Пользуясь гипотезой плоских сечений, определить, при каком значении моментов произойдет разрыв ленты, если предел прочности материала равен  

Ответ: М_раз=10 кНм.

 

Задача 44.

Балка состоит из стальной трубы 1 (d=100 мм, α=0,84) и плотно вставленного в него медного сердечника 2, жестко скрепленного с трубой. Найти наибольшие напряжения в трубе и сердечнике, полагая М=18 кНм, Е₁=200 ГПа, Е₂=100 ГПа.

Ответ:

 

Задача 45.

В первом варианте балка проектируется из трех досок сечением 80х40 мм. Во втором варианте для повышения ее несущей способности доски скрепляются стальным листом, как показано на рисунке. Оценить в процентах повышение грузоподъемности балки за счет указанного усилия, если Е_с=20Е_д.

Ответ: Грузоподъемность повышается на 100%.

 

Задача 46.

Балка состоит из двух брусьев, жестко соединенных друг с другом по всей поверхности их соприкосновения. Модуль упругости материала верхнего бруса втрое больше модуля упругости нижнего Е_в=3Е_н. Определить наибольшие напряжения в каждом из составляющих брусьев, если F=26 кН, b=12 см, h=5 см.

Ответ:

 

Задача 47.

К деревянному брусу сечением 10х18 см снизу прикреплена стальная полоса шириной 10 см и толщиной t=4 мм. Определить наибольшие напряжения в брусе и стальной полосе, если q=4,8 кН/м, Е_с/Е_д=20.

Ответ:

 

Задача 48.

Стенки поперечного сечения балки выполнены из фанеры и прибиты к деревянным брускам гвоздями, допускаемая нагрузка которых на срез [Т]=100 Н. Найти наибольшее допускаемое расстояние между гвоздями а, если Q_у=1020 Н.

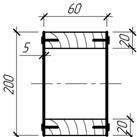
Ответ: [а]=5 см.

 

Задача 49.

Стальная балка изгибается под действием собственного веса. Найти абсолютное удлинение верхнего волокна mn, если наибольшее напряжение в балке равно 240 МПа.

Ответ:

 

Задача 50.

Шарнирно-опертая по концам чугунная балка с сечением тавра из двух неравнобоких уголков нагружается в плоскости симметрии. Какое положение балки при одной и той же нагрузки будет опасным?

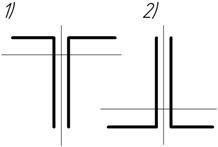
Ответ: первое положение.

 

Задача 51.

Нормальные напряжения, возникающие под действием силы F в точке С балки треугольного сечения равны . Определить величину наибольших по абсолютному значению нормальных напряжений в опасном сечении балки.

Ответ:

 

Задача 52.

Пустотелая балка прямоугольного поперечного сечения пролетом l=4 м свободно оперта по концам. Какую сосредоточенную силу F можно безопасно приложить посредине пролета в вертикальной плоскости при допускаемом напряжении  Размеры сечения показаны на рисунке в сантиметрах.

Ответ: F=54 кН

 

Задача 53.

Определить допускаемое значение силы F в двух вариантах: 1) все три бруса между собой склеены; 2) брусья между собой не скреплены. Принять а=1 м, в=24 см, h=5 см, [σ]=10 МПа, [τ]=1 МПа, [τ_кл]=0,8 МПа.

Ответ:

 

Задача 54.

Найти положение опор А и В, при котором напряжения в балке будкт минимальными по абсолютному значению

Ответ: z=0,207l

 

Задача 55.

Подобрать двутавровое сечение балки несущей равномерно распределенную нагрузку q=20 кН/м, если а=2 м,

Ответ: двутавр № 22а

 

Задача 56.

Определить диаметр бревна, из которого должен быть выпилен брус прямоугольного сечения вхh так, чтобы момент сопротивления его был наибольшим, если F=20 кН, а=1,5 м,

Ответ: d=36 см

 

Задача 57.

Тонкая прямая линейка длиной l и толщиной δ согнуто в круговое кольцо. Каково наибольшее значение возникающих при этом напряжений, если они не превышают предела пропорциональности.

Задача 58.

Определить положение нагрузки, при котором наибольшее нормальное напржение в опасном сечении принимает экстремальное значение. Найти значение этого напряжения, считая F=10 кН, а=2 м, l=10м.

Ответ: z=4,5 м;

 

Задача 59.

Определить наивыгоднейшую по условию прочности балки длину а консоли. При найденном значении а подобрать сечение балки, если q=40кН/м, l=6 м, [σ]=160 МПа. Установить также, во сколько раз вес данной балки меньше по сравнению с тем случаем, когда опоры расположены по ее концам.

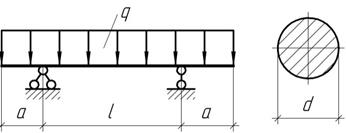
Ответ: а=2,12 м; d₀=18 см; меньше в 3,24 раза

 

Задача 60.

Шарнирно-опертая по концам чугунная балка с сечением в виде равностороннего треугольника нагружается в плоскости симметрии. Какое положение балки при одной и той же нагрузки будет наиболее опасным?

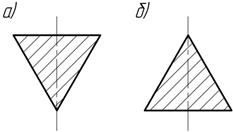
Ответ: положение а) наиболее опасное

 

Задача 61.

Призматическая балка с сечением в форме трапеции подвергается чистому изгибу, вызывающему сжатие в верхней части. Вычислить отношение в₁/в₂, при котором вес балки минимален, если отношение

Ответ:

 

Задача 62.

Определить соотношение частей изгибающего момента, воспринимаемого полками и стенкой двутавра при его изгибе.

Ответ:

 

Задача 63.

Балки указанных сечений изгибаются в вертикальной плоскости. Определить отношение радиусов  при котором обе балки имеют один и тот же момент сопротивления.

 

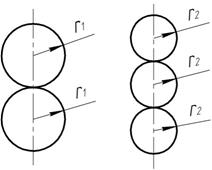
Задача 64.

Балка квадратного сечения, защемленная одним концом, на свободном конце нагружена сила F. В первом варианте сила F направлена параллельно стороне квадрата, а во втором совпадает с его диагональю. Как изменится величина силы F при переходе от первого варианта ко второму при условии, что наибольшие нормальные напряжения в обоих случаях одинаковы?

Ответ: уменьшится на 29,3%

 

Задача 65.

Стальная балка сечением 6х10 см выдерживает нагрузку F=10 кН. На расстоянии 2,05 м от левой опоры требуется просверлить круглое отверстие. Определить наибольший диаметр отверстия, при котором грузоподъемность балки не меняется.

Ответ:

 

Задача 66.

Сравните допускаемые нагрузки для двух вариантов расположения поперечного сечения чугунной балки, если [σ_с]=4[σ_р]

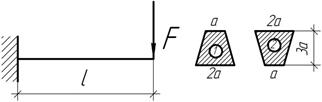
Ответ:

 

Задача 67.

Пустотелая балка прямоугольного поперечного сечения пролетом l=4 м свободно оперта по концам. Какую сосредоточенную силу F можно безопасно приложить посередине пролета в вертикальной плоскости при

 

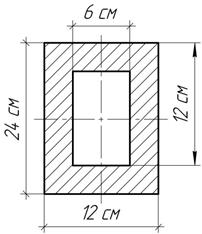
Задача 68.

Определите моменты сопротивления сечений относительно главной центральной оси.

 

Задача 69.

Для балок, сечения которых показаны на рисунке, построить качественно эпюры распределения нормальных напряжений по высоте, считая изгибающий момент отрицательным.

 

Задача 70.

Балка заданного профиля испытывает чистый изгиб. Определите указанные ниже величины.

 

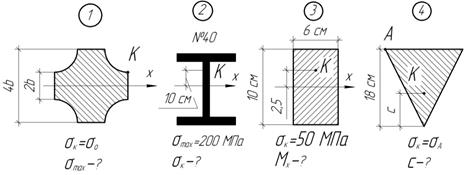
Задача 71.

Для балки прямоугольного сечения, испытывающий чистый изгиб, определите указанные ниже величины: а) Х_К=-2 см, У_К=2 см, М_Х=10 кНм. Определить  б)  Определить М_Х-?

 

Задача 72.

Определите указанные ниже величины.

 

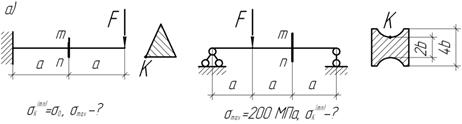
Задача 73.

Как выгоднее расположить сечение?

 

Задача 74.

Какой вариант нагружения плавающего бруса более выгоден с точки зрения его прочности?

 

Задача 75.

При непосредственном нагружении балки АВ силой F наибольшие нормальные напряжения превышают допускаемое на 50%. Какой длины следует выбрать вспомогательную балку СД, чтобы установить указанную перегрузку?

 

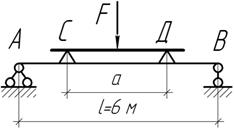
Задача 76.

Деревянный брус квадратного сечения 6х6 см выдерживает нагрузку F=360 Н. Снизится ли несущая способность балки, если в ней просверлить отверстие диаметром d=4 см в сечении mn?

 

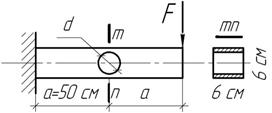
Задача 77.

Две одинаковые балки сечением 6х10 см стягиваются при помощи болта диаметром d=5 мм. Что произойдет раньше: излом  балок или разрыв болта, если предел прочности при изгибе балок  а при растяжении болта

 

Задача 78.

Несущая способность балки по варианту 1 равна  Чему равна несущая способность той же балки при смещении опоры В влево на расстояние а (вариант 2)?

 

Задача 79.

Рассматриваются две балки разной формы поперечного сечения (прямоугольная 6х10 см и круглого диаметром d=10 см) при прочих равных условиях. Какая балка обладает большей грузоподъемностью?

 

Задача 80.

Для какой балки требуется более прочное поперечное сечение?

 

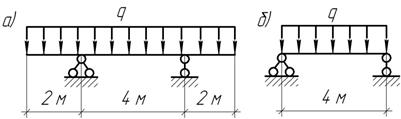
Задача 81.

Какое сечение чугунной балки наиболее рационально с точки зрения прочности на изгиб?

 

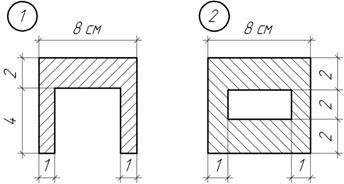
Задача 82.

Тензометр Т имеет коэффициент увеличения k=1000 и базу s=20 мм. Определить показания тензометра, если наибольшее нормальное напряжение в балке равно

 

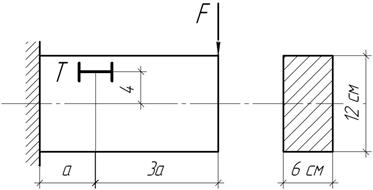
Задача 83.

Полагая гибкая пружина изогнута по дуге окружности радиуса R. Под действием какой нагрузки пружина будет прижата к плоскости?

 

Задача 84.

Постройте качественно закон распределения наибольших нормальных напряжений по длине балки и установите опасное сечение. Концентрацию напряжений в месте резкого изменения формы не учитывать.

 

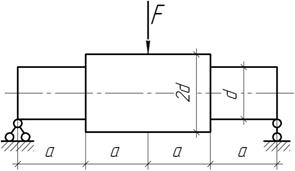
Задача 85.

Какой должна быть форма полностью равнопрочной консольной балки, нагруженной равномерно распределенной нагрузкой интенсивности q? Рассмотреть 2 случая: 1) b=const, h – переменная; 2) h=const, b – переменная.

 

Задача 86.

Показать направление касательных напряжений, передающих через ступенчатые разрезы abcd и mnpq от правой части балки на левую и обратно.

 

Задача 87.

Определить наибольшее касательное напряжение и построить эпюру τ для балки данного сечения, полагая, что поперечная сила равна Q=100 кН.

 

Задача 88.

Зная касательное напряжение в точке А (Х_А=2 см, У_А=-2 см), равное  определите касательное напряжение в точке В с координатами Х_В=-1 см, У_В=2 см.

 

Задача 89.

Зная поперечную силу Q, определите наибольшее касательное напряжение в балках данного профиля.

 

Задача 90.

Чему равна сила F, если

 

Задача 91.

Составная консоль склеена из двух балок. Предел прочности клея на сдвиг равен  При каком значении силы F нарушается прочность клеевого соединения?

 

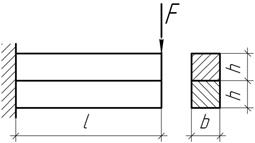
Задача 92.

При каком отношении а/h следует рассчитать деревянную балку на прочность по касательным напряжениям, если допускаемое касательное напряжение связано с допускаемым нормальным следующим соотношением [τ]=0,1[σ]?

 

Задача 93.

Круглый стержень диаметра d проталкивается по криволинейному каналу радиуса R, сделанному в абсолютно жестком теле. Каков должен быть минимальный радиус R канала, чтобы в стержне не возникали пластические деформации? Трением пренебречь.

 

Задача 94.

Балка состоит из двух стержней, модули упругости которых Е₁ и Е₂. Найти напряжения в стержнях, полагая, что проскальзывание между ними при изгибе отсутствует.

 

Задача 95.

Две балки квадратного сечения bxb свободно уложены друг на друга и загружены нагрузкой q. В загруженном состоянии балка по длине сваривается. Каковы остаточные напряжения в балках после снятия нагрузки? Трением между балками и сварочными напряжениями  пренебречь.

 

Задача 96.

На поверхности балки, момент сопротивления которой равен W_х, установлен тензометр с базой s. Чему равна сила F, если после ее приложения тензометр показал абсолютную деформацию Δs. Модуль упругости материала балки равен Е.

 

Задача 97.

Тяжелый однородный стержень постоянного поперечного сечения, покоящийся на двух опорах, используется как эталон длины. При каком расстоянии между опорами длина стержня, измеренная по его верхней поверхности, не будет меняться в процессе его деформации?

 

Задача 98.

На сколько изменится расстояние между точками А и В консольной балки, нагруженный собственным весом G?

 

Задача 99.

На сколько процентов повысится способность балки, если нагрузку F приложить согласно схеме 2. При расчете принять l=1 м.

 

Задача 100.

Найти наивыгоднейшее (по прочности) соотношение между длиной консоли а и пролетом l. Материал пластичный, сечение симметрично относительно нейтральной оси.

 

Задача 101.

Однородная прямая балка длиной l и весом G=ql лежит на жесткой плоскости. определить длину приподнятой части балки и величину наибольших нормальных напряжений при приложении к концу балки момента ql²/8.

 

Задача 102.

При нагружении балки тензометр показал удлинение Δs на базе s. Как по этому показанию прибора определить величину момента М? упругие константы материала известны.

 

Задача 103.

Построить эпюру касательных напряжений в поперечном сечении балки, работающей на изгиб. Сечение балки имеет форму ромба.

 

Задача 104.

Свободно опертая балка длиной l и высотой h имеет температуру Т₂ на нижней поверхности и Т₁ – на верхней (Т₂ >Т₁). Чему равен радиус кривизны? Какие изгибающие моменты появятся в балке, если концы ее будут защемлены?

 

Задача 105.

Консоль прямоугольного поперечного сечения нагружена сосредоточенной силой F на свободном конце. Ширина балки постоянна b, а высота меняется по линейному закону от  до  Установите положение опасного сечения и определите величину наибольшего нормального напряжения.

 

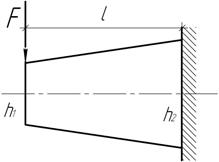
Задача 106.

Деревянный брус удерживает груз F на плаву. Определите максимальные нормальные напряжения в среднем сечении балки. На сколько эти напряжения отличаются от аналогичных напряжений в брусе постоянного сечения, обладающего такой же плавучестью?

 

Задача 107.

Постройте эпюру касательных напряжений в произвольном поперечном сечении mn балки. Считать касательную нагрузку t равномерно распределенной по длине и ширине балки.

 

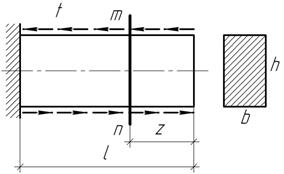
Задача 108.

Консоль прямоугольного поперечного сечения нагружена силой F на конце. Определить нормальные  и касательные  напряжения в точке К сечения АВСД, составляющего с поперечным сечением угол α.

 

Задача 109.

Найти распределение нормальных напряжений по сечению составной балки при чистом изгибе в вертикальной плоскости и указать положение нейтральной оси, считая соединение абсолютно жестким.

 

 

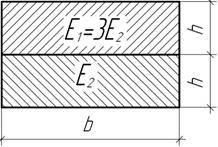
Задача 110.

Построить эпюры вертикальной составляющей касательного напряжения в частях от наибольшего значения τ_max=τ₀ для указанных форм поперечного сечения балки.

Ответ:

N п/п	by			τ/
1	0,5b	0	0	0
2	0,5b	3b3/16	3b2/8	1
3	b	3b3/16	3b2/16	1/2
4	b	5b3/16	5b2/16	5/6
3¢	b	3b3/16	3b2/16	1/2
2¢	0,5b	3b3/16	3b2/8	1
1¢	0,5b	0	0	0

 

Для остальных сечений студентам предлагается построить эпюры самостоятельно.

 

Задача 111.

Для некоторого сечения балки известно напряжение в точке А, равное σ_A= 100 МПа. Требуется определить по величине и по знаку напряжения в точках В и С.

 

Задача 112.

Зная напряжение в точке К сечения mn, равное σ₀, определить наибольшее напряжение, возникающее в балке.

 

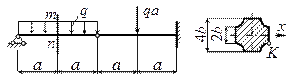
Задача 113.

Для балок, сечения которых показаны на рисунке, построить эпюры распределения нормальных напряжений по высоте, считая изгибающий момент положительным (отрицательным). Установить, как выгоднее расположить сечения, имеющие только одну ось симметрии, в плоскости которой действует изгибающий момент, если материал балки чугун, лучше работающий на сжатие, чем на растяжение.

 

Задача 114.

Стальной рычаг тормозного устройства состоит из штанги прямоугольного поперечного сечения 20х60 мм, опирающейся в точке В (см. рисунок) на шарнирный болт, пропущенный сквозь отверстие в штанге. Центр отверстия расположен на оси штанги; диаметр его d = 30 мм. Найти, какие силы можно безопасно приложить к концам рычага при допускаемом напряжении [σ] = 140 МПа. и при учете ослабления сечения болтовым отверстием.

Ответ: F₁ = 1470 Н; F₂ = 5880 Н.

 

Задача 115.

Подобрать сечение балки двутаврового профиля и произвести полную проверку прочности при следующих данных (см. рисунок): F = 200 кН;   а=0,3 м;  l =3,0 м; [σ]=140 МПа; [τ] =80 МПа.

Ответ: 27b.

 

Задача 116.

Балка пролетом l= 6 м, свободно лежащая на двух опорах, загружена четырьмя одинаковыми симметрично расположенными силами F =140 кН (см. рисунок). Подобрать сечение балки из двух швеллеров, удовлетворяющее условиям прочности по нормальным касательным и главным напряжениям, если расстояние между силами а = 0,5 м, а допускаемые напряжения приняты [σ] = 160 МПа и [τ] = 100 МПа. Воспользоваться 3-й теорией прочности.

Ответ: 2 № 36а.

 

Задача 117.

При работе строгального станка на резец передается нагрузка F=2,75 кН, вылет резца h=70 мм, поперечное сечение прямоугольное 20х15мм (см. рис.). Проверить прочность стержня резца, если предел текучести σ_T = 600 МПа, а коэффициент запаса прочности n=3.

Ответ: Наибольшее напряжение σ_max = 191,8 МПа < [σ] = 200 МПа.

 

Задача 118.

Гаечный ключ нагружен усилием рабочего F=0,25 кН. Проверить прочность в опасном сечении I–I  (прямоугольное с размерами 18х5 мм), если [σ] = 120 МПа (см. рис.).

Ответ: Напряжение σ_max= 118,5 МПа < [σ] = 120 МПа.

 

Задача 119.

Определить максимальные напряжения в рессоре автомобиля при торможении (см. рис. а), если реакция колеса G_к = 10 кН, тормозное усилие T_к = 8 кН, расстояние до точки крепления пальца рессоры h =580 мм. Размеры рессоры: длина l₁ = l₂ = 550 мм, число листов 13, поперечное сечение всех листов одинаково 65 х 6 мм, ширина накладки с =120 мм. Расчетная схема приведена на рис., б. Момент сопротивления сечения рессоры принимают равным сумме моментов сопротивления листов. Опасное сечение I-I по концу накладки.

Ответ: Максимальное напряжение σ_max = 891 МПа.

 

Задача 120.

Построить  эпюры  Q  и M_{x .} Определить  F_adm,  если  σ_adm= 100 МПа , L=2м  

 

 

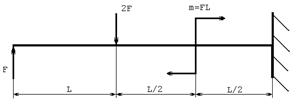
Задача 121.

Проверить  грузоподъемность балки, если  W_x = 14 см³; σ_adm = 140 МПа . 

 

 

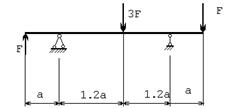
Задача 122.

Определить размеры поперечного сечения b и h = 2b, если  σ_adm = 120 МПа;  L=2м; F₁ =6кН;  F₂=10кН; q=10кН/м

 

Задача 123.

Проверить прочность балки прямоугольного сечения, если l=1м,  q=5кН/м,  σ_adm = 160МПа

 

Задача 124.

Проверить прочность балки, если М=5 кНм; F=5 Кн; q=5кН/м; σ_adm =140 МПа; L=3м; D=0,1м.

 

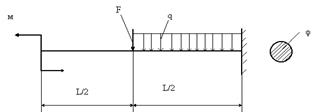
Задача 125.

Для балки на двух опорах пролетом 3а (а = 1 м), нагруженной равномерно распределенной нагрузкой интенсивностью q = 10 кН/м и сосредоточенной силой Р = 20 кН построить эпюры поперечной силы Q_y и изгибающего момента M_x. Определить сторону квадратного поперечного сечения балки.

  

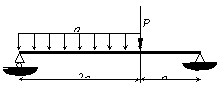
Задача 126.

Определить минимальную высоту h балки прямоугольного поперечного сечения (см. рис.). Принять b = h/3; l = 4 м, F = 6 кН, материал балки – сталь с R_y = 240 МПа, γ_с= 1.

       Ответ: h=0,0765 м.

 

Задача 127.

Определить допускаемый минимальный диаметр d консольной балки (см. рис.) из алюминия марки АЛ8 с R_y = 135 МПа. Принять F = 1 кН, l = 1м, γ_с = 1. Собственный вес балки не учитывать.

Ответ: d = 6,1 см.

 

Задача 128.

Подобрать поперечное сечение однопролетной стальной балки, нагруженной равномерно распределенной нагрузкой q= 16 кН/м (см. рис.), l = 4 м. Вычислить собственный вес балки из стали С255, γ_с = 1.

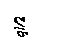
При расчете принять, что:

а) поперечное сечение балки – прямоугольное с отношением высоты h к ширине b балки, равным 3 (h = 3b);

б) поперечное сечение балки – круглое сплошное;

в) балка выполняется из электросварных прямошовных труб;

г) балка – прокатная двутавровая.

Проанализировать полученные результаты.

Ответ: а) h = 13,5 см; b = 4,5 см; масса балки 191 кг; б) d = 11 см, масса балки 298 кг; в) D = 219 мм с t = 4 мм, масса балки 84,8 кг;  г) двутавр № 18, масса балки 73,6 кг.

 

Задача 129.

Определить минимальную ширину b деревянной балки прямоугольного поперечного сечения (см. рис.). Принять h = 3b, l = 4 м, F = 6 кН, материал балки – сосна с R_И  = 14 МПа, R_ск = 1,8 МПа.

Ответ: b = 0,066 м.

 

Задача 130.

Определить минимальную ширину b деревянной балки прямоугольного поперечного сечения, загруженной равномерно распределенной нагрузкой q = 5 кН. Принять h = 2b, l = 4 м, материал балки – сосна с R_И = 14 МПа, R_ск = 1,8 МПа (см. рис.).

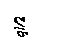
Ответ: b = 0,1 м.

 

Задача 131.

Построить эпюры главных напряжений σ_max, σ_min и эпюру максимальных касательных напряжений τ_max в наиболее опасном с точки зрения главных напряжений прямоугольном поперечном сечении балки, изображенной на рисунке. При расчете принять l = 4 м, F = 40 кН, b = 5 см, h = 15 см. Материал балки – сталь с R_y  = 240 МПа.

Ответ:    

 

Задача 132.

Построить эпюры главных напряжений σ_max, σ_min и эпюру максимальных касательных напряжений τ_max в наиболее опасном с точки зрения главных напряжений круглом поперечном сечении консольной балки, изображенной на рисунке. При расчете принять l = 2 м, сосредоточенные силы F = 5 кН, диаметр балки d = 12 см. Материал балки – сталь с R_y = 240 МПа, γc=1 (см. рис. ).

      

Ответ:     

                

 

Задача 133.

Построить эпюры главных напряжений и максимальных касательных напряжений в наиболее опасном треугольном поперечном сечении (рис.1) балки с М = 40 кНм, Q = 40 кН. Принять без вывода, что  Записать в аналитической форме выражение для σ_x, а затем вычислить σ_max, σ_min , τ_max в точках с  y = 2h/3, y = h/6, y = 0, y = –h/3.

      

 

Задача 134.

Для двухопорных балок, изображенных на рисунке, построить эпюры поперечных, сил и изгибающих моментов и подобрать их сечения. Допускаемые напряжения принять: для прокатных профилей [σ] =160 МПа, для квадратных и круглых (сосна) [σ] = 12 МПа. Длины участков балок показаны в метрах.

 

Определение перемещений и проверка жесткости балок при изгибе

 

Задача 1.

Нарисуйте форму упругой линии для следующих балок.

 

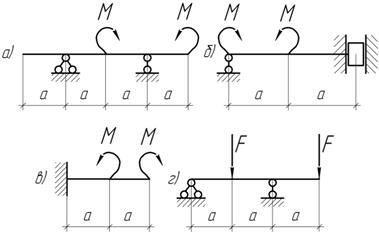
Задача 2.

Как загружена балка, если ее упругая линия образованна дугами окружностей радиуса R?

 

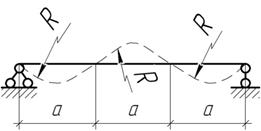
Задача 3.

Сравните форму упругой линии для двух балок.

 

Задача 4.

Выяснить форму упругой линии балки на участке ВС и определите радиус кривизны, если жесткость поперечного сечения равнаEI_х.

 

Задача 5.

Чему равен радиус кривизны балки прямоугольного профиля в среднем сечении С? Дано: Е, q, l, b, h.

 

Задача 6.

Какую форму должна иметь балка прямоугольного сечения постоянной высоты h и переменной ширины b, чтобы ее ось изгибалась по дуге окружности?

 

Задача 7.

Какой знак необходимо выбрать в дифференциальном уравнении упругой линии балки  для указанных случаев?

 

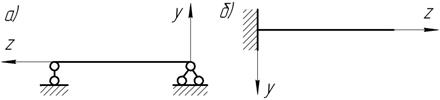
Задача 8.

При каком размере а прогиб балки на участке АВ изменяется по линейному закону?

 

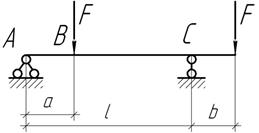
Задача 9.

Балка длиной l=2 м, шарнирно опертая по концам, изгибается согласно уравнению . Какая нагрузка вызывает такой изгиб?

 

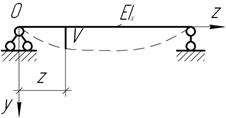
Задача 10.

Используя теорему Кастилиано, определите угол поворота сечения В.

 

Задача 11.

Получить уравнение изгиба упругой оси консольной балки после деформации. Балка представлена на рисунке, жесткость балки на изгиб постоянна (EI = const).

Ответ: y = –mx²/(2EI), 𝜑= –mx/(EI).

 

Задача 12.

Получить уравнение изгиба упругой оси консольной балки, нагруженной равномерно распределенной нагрузкой q (рис. 1). Определить максимальный прогиб балки.

Определить максимальный прогиб консольной балки, нагруженной сосредоточенным моментом m. Жесткость балки на изгиб равна EI. Определить также угол поворота оси балки в точке В (рис. 2).

Получить уравнение изгиба упругой оси однопролетной балки, показанной на рис. 3. Жесткость балки на изгиб EI считать постоянной по всей длине.

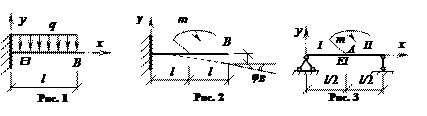
       Ответ к рис.1: y = q(4x³l –x⁴ – 6l²x²)/(24EI);    y_B,max = –ql ⁴/(8EI).

       Ответ к рис.2: y_B,max = –3ml²/(2EI); = –ml/(EI).

       Ответ к рис.3:             

    

Задача 13.

Получить уравнение изгиба упругой оси консольной балки с постоянной жесткостью на изгиб EI. Балка и действующая на нее нагрузка изображены на рисунке. Определить прогиб в точке А.

Ответ: y_I = qbx²(6a + 3b –2x)/(12EI),     

                y_II = q[a₄ – 4a³x + 6(a + b)²x² – 4(a + b)x³ + x⁴]/(24EI);

                y_I,A = y_II,A = qa²b(4a + 3b)/(12EI).

 

Задача 14.

Определить максимальный прогиб однопролетной балки, нагруженной посередине пролета сосредоточенной силой F (см. рис.).

Ответ:  y_B = –Fl³/(48EI_z);  I_z = bh³/12.

 

Задача 15.

Определить максимальный прогиб консольной балки круглого поперечного сечения диаметром d. Внешняя нагрузка показана на рисунке.

Ответ:   

      

Задача 16.

Определить максимальный прогиб в однопролетной балке, показанной на рис. 1. Жесткость балки на изгиб – EI_z.

Записать уравнения изгиба упругой оси однопролетной балки, представленной на рис. 2. Балка имеет постоянную жесткость на изгиб EI_z.

Записать уравнения изгиба упругой оси консольной балки с постоянной жесткостью на изгиб EI. На балку действует сосредоточенная сила F. Определить угол поворота поперечного сечения на участке II (рис. 3).

Ответ к рис.1: y(x = l/2) = –13ql⁴/(384EI_z).

Ответ к рис.2:      

Ответ к рис.3:  

 

Задача 17.

Получить уравнения изгиба упругой оси балки для каждого из ее трех участков. Балка – постоянной жесткости на изгиб EI (см. рис.).

Ответ:             

 

Задача 18.

Подобрать сечение двутавровой балки из условия прочности и условия жесткости. При расчетах принять [1/n_o] = 1/250. Балка показана на рисунке. Материал – сталь С255.

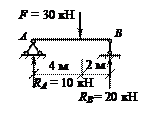
Ответ: двутавр № 20 – из условия прочности для М_max = 40 кНм; двутавр № 22 – из условия жесткости для у_max = 116/(EI).

 

Задача 19.

Подобрать сечение прокатной балки из условия прочности и условия жесткости (см. рис.). При расчетах принять [1/n_o] = 1/150, длина консоли l = 4 м,  сосредоточенный изгибающий момент m = 10 кНм. Материал – сталь С285 с R_y = 280 МПа, γ_с= 1.

Ответ: двутавр № 10 – из условия прочности; двутавр № 16 – из условия жесткости для у_max = 80/(EI).

 

Задача 20.

Подобрать сечение прокатной балки из условия прочности и условия жесткости (см. рис.). При расчетах принять [1/n_o] = 1/200, a = 4 м, b = 2 м, F = 10 кН. Материал – сталь С285 с R_y = 280 МПа, γ_с= 1.

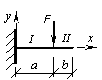
Ответ: двутавр № 18 – из условия прочности; двутавр № 24 – из условия жесткости для у_max = 373/(EI).

 

Задача 21.

Подобрать сечение балки прямоугольного поперечного сечения с отношением сторон h/b = 3. Балка нагружена сосредоточенной силой F = 10 кН, l = 4 м (см. рис.). Материал – сталь С255, [1/n_o] = 1/200.

Ответ: b = 3,03 см – из условия прочности; b = 3,5 см – из условия жесткости.

 

Задача 22.

Подобрать сечение прокатной балки из условия прочности и проверить условие жесткости для нее (см. рис.). При расчетах принять m = 40 кНм, пролет балки l = 4 м, [1/n_o] = 1/200. Материал балки – сталь С255, γ_с= 1. Сортамент прокатного профиля подобрать по таблице сортамента «Двутавры стальные горячекатаные».

Ответ: двутавр № 14 – из условия прочности; двутавр № 10 – из условия жесткости для у_max = 80/(9EI).

 

Задача 23.

Подобрать допускаемый вылет l консоли, заделанной одним концом и находящейся под действием только собственного веса q. Консоль изготовлена из электросварной прямошовной трубы с наружным диаметром D = 168 мм, толщиной стенки t = 6 мм. Материал консоли – сталь С255, коэффициент условий работы γ_с= 1. Расчетная схема консоли показана на рисунке. Принять [1/n_o] = 1/200.

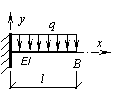
Ответ:  l = 15,6 м – из условия прочности;  l = 8,8 м – из условия жесткости.

 

Задача 24.

Подобрать диаметр  d  консольной балки  (см. рис.) при  F = 10 кН, l = 2 м из условия прочности и условия жесткости. Материал консоли – сталь С255, γ_с= 1, [1/n_o] = 1/200.

Ответ:  d = 13,7 см – из условия прочности; d = 16,2 см – из условия жесткости.

 

Задача 25.

Определить допускаемый вылет l_ef консоли из условия жесткости (см. рис.). При расчете принять, что консоль представляет собой двутавр № 20 из стали С255, q = 2,4 кН/м; [1/n_o] = 1/250.

Ответ:  l_ef  = 3 м.

 

Задача 26.

Определить допускаемую нагрузку F на однопролетную балку (см. рис.) из условия жесткости. При расчете принять, что l = 4 м, b = 10 см, h = 20 см, материал балки – сталь С285, предельный относительный прогиб [1/n_o] = 1/250.

Ответ: F = 164,8 кН.

 

Задача 27.

Определить допускаемый пролет l однопролетной балки (см. рис.) из условия жесткости. При расчете принять F = 165 кН, высота балки h = 2b = 20 см, материал балки – сталь С285, предельный относительный прогиб [1/n_o] = 1/250.

Определить максимальное нормальное напряжение.

Ответ: l = 4 м; σ_x,max= 247,5 МПа <280 МПа = R_y.

 

Задача 28.

Определить допускаемую нагрузку m на консольную балку из двутавра № 16 из условия жесткости (см. рис.). Принять l = 4 м, предельный относительный прогиб [1/n_o] = 1/150.

Ответ: m = 12 кНм.

 

Задача 29.

Определить допускаемую нагрузку F на консоль из двутавра № 24 (см. рис.) из условия прочности и из условия жесткости. При расчетах принять, что a = 4 м, b = 2 м, [1/n_o] = 1/200. Консоль изготовлена из стали С255 с R_y = 240 МПа.

Ответ: F  = 11,5 кН – из условия жесткости;   F = 17,3 кН – из условия прочности.

 

Задача 30.

Определить прогибы в точках обозначенных буквой А, а также угол поворота сечений, обозначенных буквой В, если Е = 2∙10⁵ МПа.

 

Расчет перемещений методом начальных параметров

 

Задача 1.

Определить значение начальных параметров М₀, Q₀, V₀, θ₀.

 

Задача 2.

Согласно методу начальных параметров балка постоянного сечения при приложении к ней внешнего момента М изгибается, принимая форму квадратной параболы  С другой стороны, нам известно следующее выражение   В нашем случае М_х=М=const. Но постоянную кривизну имеет дуга окружности, а не парабола. Как же изогнется балка? По дуге параболы или по окружности?

 

Онлайн-калькулятор "Подбор кольцевого сечения балки при изгибе"

 

---