Главная

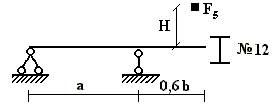
Задача 1. Определение напряжений в балке при действии ударной нагрузки.

На балку, выполненную из прокатных профилей, свободно лежащую на двух опорах (рис.1) с высоты H падает груз F₅. Требуется найти наибольшее нормальное напряжение в балке.

Данные взять из табл. 1.

Таблица 1

Номер строки	Схема по рис.1	а, м	b, м	H, м	F5, кг
01	1	1,1	1,1	1,1	1,1
02	2	1,2	1,2	1,2	1,2
03	3	1,3	1,3	1,3	1,3
04	4	1,4	1,4	1,4	1,4
05	5	1,5	1,5	1,5	1,5
06	6	1,6	1,6	1,6	0,6
07	7	1,7	1,7	1,7	0,7
08	8	1,8	1,8	1,8	0,8
09	9	1,9	1,9	1,9	0,9
10	10	1,0	1,0	1,0	1,0
11	11	1,1	1,1	1,1	1,1
12	12	1,2	1,2	1,2	1,2
13	13	1,3	1,3	1,3	1,3
14	14	1,4	1,4	1,4	1,4
15	15	1,5	1,5	1,5	1,5
16	16	1,6	1,6	1,6	0,6
17	17	1,7	1,7	1,7	0,7
18	18	1,8	1,8	1,8	0,8
19	19	1,9	1,9	1,9	0,9
20	20	1,0	1,0	1,0	1,0
21	21	1,1	1,1	1,1	1,1
22	22	1,2	1,2	1,2	1,2
23	23	1,3	1,3	1,3	1,3
24	24	1,4	1,4	1,4	1,4
25	25	1,5	1,5	1,5	1,5
26	26	1,6	1,6	1,6	0,6
27	27	1,7	1,7	1,7	0,7
28	28	1,8	1,8	1,8	0,8
29	29	1,9	1,9	1,9	0,9
30	30	1,0	1,0	1,0	1,0
31	31	1,4	1,4	1,4	1,4
32	32	1,5	1,5	1,5	1,5
33	33	1,6	1,6	1,6	0,6
34	34	1,7	1,7	1,7	0,7
35	35	1,8	1,8	1,8	0,8
36	36	1,9	1,9	1,9	0,9
	в	б	а	г	а

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис.1

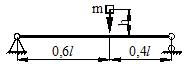
Задача 2. Определение напряжений и прогибов в балке при действии ударной нагрузки.

Для стальной двутавровой балки (рис.2), определить максимальные ударные напряжения и максимальный прогиб в месте падения груза.

Данные взять из табл. 2.

Таблица 2

Номер строки	Схема по рис.2	№ двутавра	m, кг	h, мм	l, м
01	1	10	20	85	4
02	2	12	25	80	4,2
03	3	14	30	75	4,6
04	4	16	35	70	4,8
05	5	18	40	65	5,0
06	6	20	45	60	5,2
07	7	22	50	55	5,4
08	8	24	55	50	5,6
09	9	27	60	45	5,8
10	10	30	65	40	6,0
11	11	12	25	80	4
12	12	14	30	75	4,2
13	13	16	35	70	4,6
14	14	18	40	65	4,8
15	15	20	45	60	4,6
16	16	22	50	55	4,8
17	17	24	55	50	5,0
18	18	27	60	45	5,2
19	19	10	20	40	5,4
20	20	12	25	80	5,6
21	21	14	30	75	5,8
22	22	16	35	70	6,0
23	23	18	40	80	4
24	24	20	45	75	4,8
25	25	22	50	70	5,0
26	26	24	55	65	5,2
27	27	27	60	60	5,4
28	28	30	65	55	5,6
29	29	12	25	50	5,8
30	30	14	30	80	6,0
31	31	16	35	75	4
32	32	18	40	70	4,2
33	33	20	40	80	4,6
34	34	22	45	75	4,8
35	35	30	50	70	4,6
36	36	12	55	65	4,8
	б	а	г	в	а

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

7 схема 8 схема 9 схема

10 схема 11 схема 12 схема

13 схема 14 схема 15 схема

16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

25 схема 26 схема 27 схема

28 схема 29 схема 30 схема

31 схема 32 схема 33 схема

34 схема 35 схема 36 схема

Рис.2

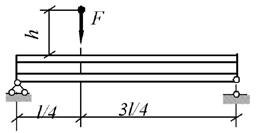
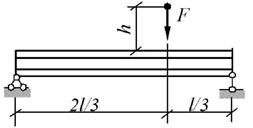
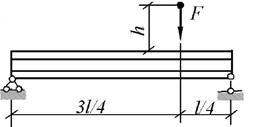
Задача 3. Определение напряжений в балке при действии ударной нагрузки.

На балку, свободно лежащую на двух жёстких опорах (табл. 3), с высоты h падает груз F.

Требуется:

1. Найти наибольшее нормальное напряжение в балке.

2. Решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой равна α.

3. Сравнить полученные результаты.

Данные взять из табл.3 и рис. 3.

Таблица 3

Номер строки	Схема по рис.3	№ двутавра	l, м	F, Н	h, м	α, м/Н
01	1	20	2,1	1000	0,10	21∙10^-6
02	2	20а	2,2	900	0,20	22∙10^-6
03	3	24	2,3	800	0,03	23∙10^-6
04	4	24а	2,4	700	0,04	24∙10^-6
05	5	27	2,5	600	0,05	25∙10^-6
06	6	27а	2,6	500	0,06	26∙10^-6
07	7	30	2,7	400	0,07	27∙10^-6
08	8	30а	2,8	300	0,08	28∙10^-6
09	9	33	2,9	1200	0,09	29∙10^-6
10	10	36	3,0	1100	0,04	30∙10^-6
	е	а	б	в	г	д

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

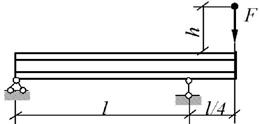
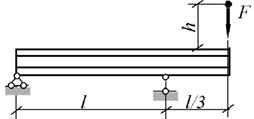
Рис. 3

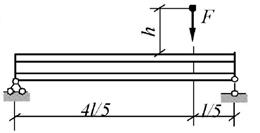
Задача 4. Определение напряжений в балке при действии ударной нагрузки.

Груз весом Q падает с высоты H (рис.4) на двутавровую стальную балку. Требуется проверить прочность балки, если [σ] = 160 МПа.

Данные взять из табл.4 и рис. 4.

Таблица 4

Номер строки	Схема по рис. 4	№ двутавра	a, м	Q, кН	H, см
01	1	12	0,4	1	2
02	2	10	0,5	1,5	3
03	3	24	0,6	2	4
04	4	26	0,7	2,5	1,5
05	5	16	0,8	3	2
06	6	27	0,4	3,5	3
07	7	18	0,9	4	3,5
08	8	22	1,1	4,5	2,5
09	9	30	0,8	5	2
10	10	14	0,7	5,5	2,3
	в	а	б	в	г

Рис.4

Задача 4. Определение напряжений в балке при действии ударной нагрузки.

На двутавровую балку (рис.5) с высоты h падает груз F.

Требуется:

1) найти наибольшее нормальное напряжение в балке;

2) решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой α (осадка от груза 1 кН);

3) сравнить полученные результаты.

Исходные данные к задаче принимаются по табл. 5 и схемам на рис.5.

Таблица 5

Номер строки	Схема по рис.5	№ двутавра	F, кН	l, м	h, см	𝛼, см/кН
01	1	30	30	4,4	5	4
02	2	27	40	4,2	4	6
03	3	33	35	3,8	3	8
04	4	24	45	3,6	6	3
05	5	22	25	4,0	5	5
06	6	20	28	5,0	4	6
07	7	30	30	4,8	3	8
08	8	27	32	4,6	6	4
09	9	33	34	4,4	7	5
10	10	24	36	4,5	8	3
	г	а	в	б	г	а

Рис.5

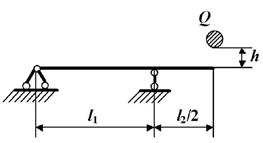
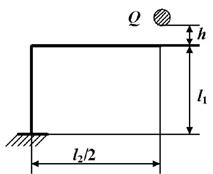
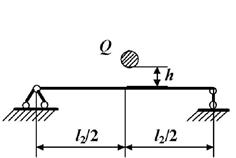
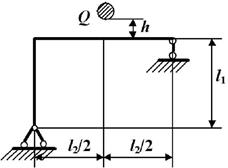
Задача 6. Определение напряжений в раме при действии ударной нагрузки.

Исходные данные к задаче принимаются по табл. 6 и схемам на рис.6.

1. Постройте эпюру изгибающих моментов в сечениях рамы (балки) для случая статического действия нагрузки.

2. Найдите максимальные нормальные напряжения в опасном сечении от статического действия нагрузки.

3. Определите статический прогиб, используя один из известных методов, и найдите динамический коэффициент.

4. Вычислите величины максимального нормального напряжения при ударе и динамического прогиба.

5*. Проверьте выполнение условия прочности. Если условие прочности при ударе не выполняется, предусмотрите меры, обеспечивающие его выполнение. Материал конструкции - сталь.

Таблица 6

Номер строки	Схема по рис. 6	l1, м	h, см	Q, кН	l2, м	№ двутавра
01	1	2	3	1,2	6	20
02	2	3	4	1,0	5	22
03	3	4	5	0,9	4	24
04	4	5	8	0,8	3	27
05	5	6	6	0,7	2	30
06	6	5	5	0,6	2	33
07	7	4	4	0,8	3	27
08	8	3	3	0,9	4	24
09	9	2	2	1,0	5	22
10	10	6	5	1,1	6	20
	б	б	в	г	а	в

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

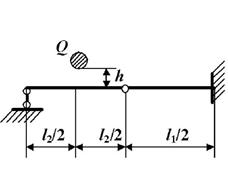
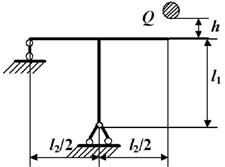
7 схема 8 схема

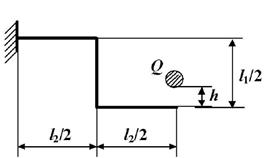
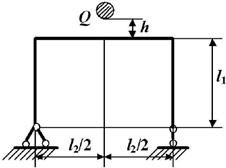
9 схема 10 схема

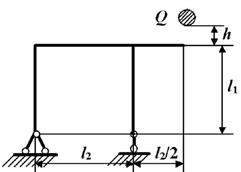
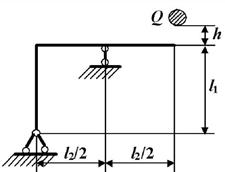
Рис. 6

Примеры выполнения задач

Пример 1

На двутавровую балку (рис.7, а) с высоты h падает груз F.

Требуется:

1) найти наибольшее нормальное напряжение в балке;

2) решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой α (осадка от груза 1 кН);

3) сравнить полученные результаты.

Дано: F = 30 кН; l = 2,4 м; h = 3 см; α= 4 см/кН; двутавр № 24.

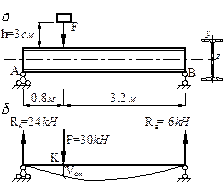
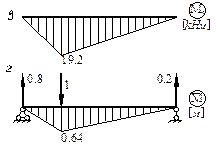
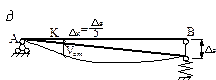
Рис.7

Решение.

Вычисляя реакции опор R_A = 24 кН, R_B = 6 кН, (рис. 7), построим эпюру изгибающих моментов M_F (рис. 7, в).

Динамическое напряжение

σ_d=k_d∙σ_ст

где

Для определения прогиба балки в точке К при статическом приложении силы F построим эпюру от единичной силы, приложенной в этой точке в направлении вектора F (рис. 7, г).

Вычислим ∆_ст, перемножив эпюры M_F и по способу Верещагина:

Момент инерции и момент сопротивления для двутавра №24 возьмем из сортамента: I_z= 3460 см⁴; W_z= 289 см³. Модуль продольной упругости для стали Е=2∙10⁵ МПа:

Если правую опору заменить пружиной, то за счет осадки пружины опора В переместится на величину (рис. 7, д):

, а точка К, расположенная на от неподвижной опоры А переместится на:

Полное перемещение точки К равно

∆_k+∆_ст = 4,6 +0,237 = 5,037 см.

В этом случае

Сопоставляя первый и второй расчеты можно сделать вывод, что установка податливой опоры снижает динамические напряжения в данном случае, более чем в 2,5 раза.

Пример 2

Груз массой m = 605 кг падает с высоты h на стальную двутавровую балку (рис. 8). Проверить прочность при [σ_дин] = 120 МПа.

Характеристика балки: двутавр № 36; погонная масса q = 46,8 кг/м; I_x =13380 см⁴; W_x = 743 см³; модуль Юнга E = 2∙10⁵ МПа = 2∙10⁴ кН/см²; h = 4 см.

Рис.8. Расчет на удар: а – заданная балка;

б – расчетная схема и ее грузовое состояние;

в – единичное состояние

Решение.

1. При весе ударника Q_m = mg = 605∙9,81 = 5940 Н = 5,94 кН, определяем статический прогиб балки в месте удара по формуле Мора в форме, предложенной А.Н. Верещагиным в 1925 г. (рис. 8):

где ω₁, ω₂ – площади эпюры M_F; – ординаты эпюры , взятые под центрами тяжести ω₁, ω₂; EI_x – изгибная жесткость балки. Тогда

Коэффициент

Прочность балки обеспечена.

Теперь проверим балку, учитывая ее массу. Отношение β = M_бал/m = 46,8∙5,9 / 605 = 0,456. Коэффициент α (табл. 7) подсчитаем так: сначала из соотношения uR = 1,2 м найдем u = 1,2 / 4,7 = 0,255, а потом по формуле, приведенной в табл. 7, получим α = 0,211, так что

Как видно, чем больше масса балки, тем меньше эффект удара. Например, этим и объясняется эффектный, но безопасный цирковой номер.

Таблица 7. Значения коэффициента α при различных случаях удара

Тип удара	Расчетная схема	Коэффициент α	u – доля пролета
Продольный
Поперечный			0<u<1
			0<u<1
			u > 0

Онлайн-калькулятор "Расчет коэффициента динамичности при падении груза на конструкцию"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00