Главная

Задача 1. Расчет стержней сжатых внецентренно приложенной силой.

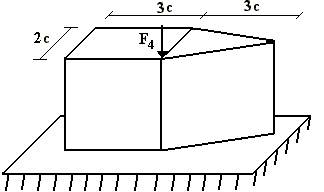
Для стойки, сжатой внецентренно приложенной силой F₄ (рис.1), требуется:

1) определить положение нейтральной линии;

2) определить значения наибольших растягивающих и наиболее сжимающих напряжений;

3) построить ядро сечения.

Данные взять из табл.1.

Таблица 1

Номер cтроки	Схема по рис.1	F4, см^2	с, м
01	1	400	0,1
02	2	500	0,15
03	3	600	0,2
04	4	700	0,25
05	5	800	0,3
06	6	450	0,1
07	7	550	0,15
08	8	650	0,2
09	9	750	0,25
10	10	850	0,3
11	11	700	0,25
12	12	800	0,3
13	13	450	0,1
14	14	550	0,15
15	15	650	0,2
16	16	750	0,25
17	17	700	0,2
18	18	800	0,25
19	19	450	0,3
20	20	550	0,1
21	21	650	0,15
22	22	750	0,2
23	23	850	0,25
24	24	700	0,3
25	25	800	0,25
26	26	450	0,3
27	27	550	0,1
28	28	650	0,15
29	29	750	0,2
30	30	750	0,25
31	31	850	0,3
32	32	700	0,1
33	33	800	0,15
34	34	450	0,2
35	35	550	0,25
36	36	750	0,3
	г	а	в

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

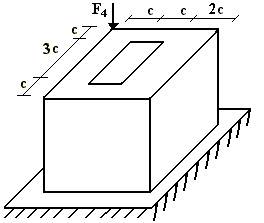
7 схема 8 схема

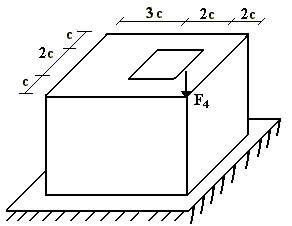
9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

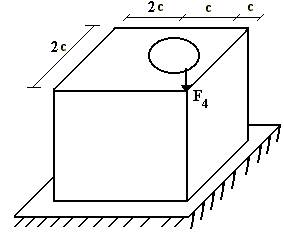
15 схема 16 схема

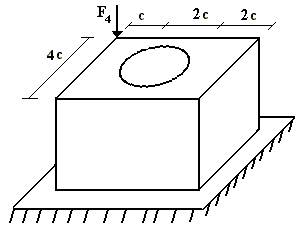
17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис.1

Задача 2. Расчет стержней сжатых внецентренно приложенной силой.

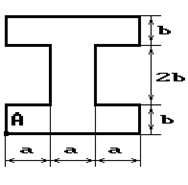
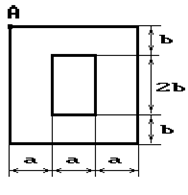
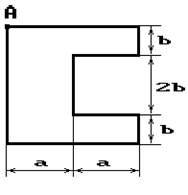
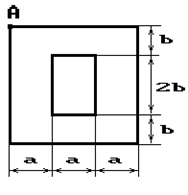
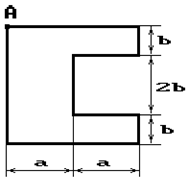
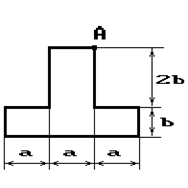
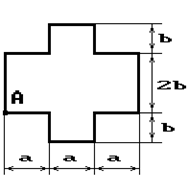
Чугунный короткий стержень, поперечное сечение которого изображено на рис.2, сжимается силой Р, приложенной внецентренно в точке А. Требуется:

1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив величины этих напряжений через Р и размеры сечения;

2) найти допускаемую нагрузку Р при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие [σ]_c и на растяжение [σ]_p.

Данные взять из табл.2.

Таблица 2

Номер cтроки	Схема по рис.2	а, см	b, см	[σ]c, мПа	[σ]p, мПа
01	1	6	6	110	21
02	2	2	2	120	22
03	3	3	3	130	23
04	4	4	4	140	24
05	5	5	5	150	25
06	6	6	6	60	26
07	7	2	2	70	27
08	8	3	3	80	28
09	9	4	4	90	29
10	10	5	5	100	30
11	11	3	4	130	23
12	12	4	5	140	24
13	13	5	6	150	25
14	14	6	2	60	26
15	15	2	3	70	27
16	16	4	4	80	28
17	17	5	5	90	29
18	18	6	6	110	21
19	19	2	2	120	22
20	20	3	3	130	23
21	21	4	4	140	24
22	22	5	5	150	25
23	23	3	6	60	26
24	24	4	2	70	27
25	25	5	3	80	28
26	26	6	4	90	29
27	27	2	5	100	30
28	28	6	4	130	23
29	29	2	5	140	24
30	30	3	6	150	25
31	31	4	2	60	26
32	32	5	3	70	27
33	33	6	4	80	28
34	34	2	5	90	29
35	35	3	6	150	23
36	36	4	2	60	24
	а	в	б	г	а

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

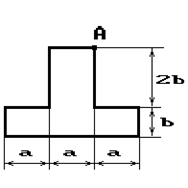
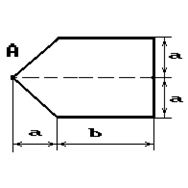
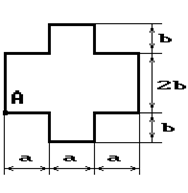
7 схема 8 схема 9 схема

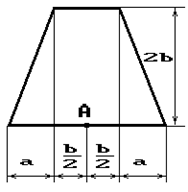
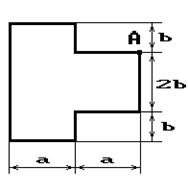
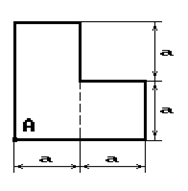
10 схема 11 схема 12 схема

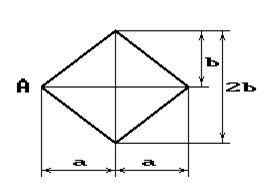
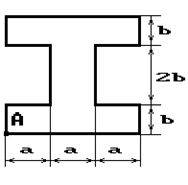
13 схема 14 схема 15 схема

16 схема 17 схема 18 схема

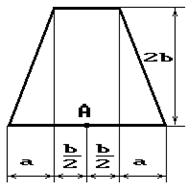
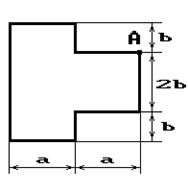
19 схема 20 схема 21 схема

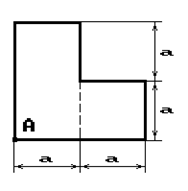
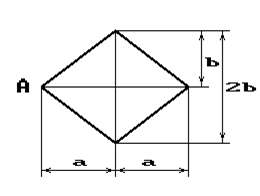
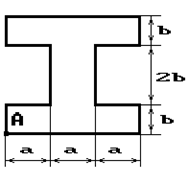
22 схема 23 схема 24 схема

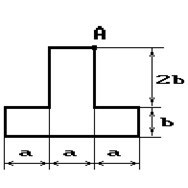
25 схема 26 схема 27 схема

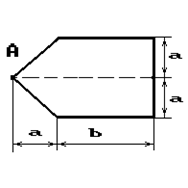
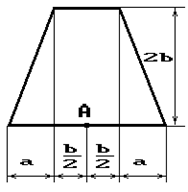
28 схема 29 схема 30 схема

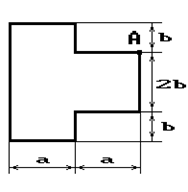
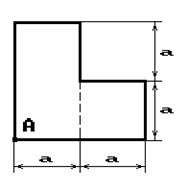
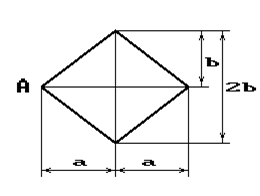
31 схема 32 схема 33 схема

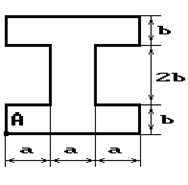
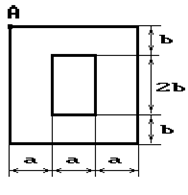
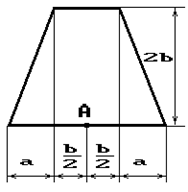
34 схема 35 схема 36 схема

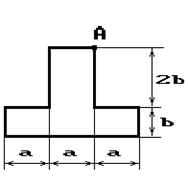
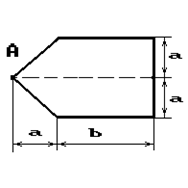
Рис. 2

Задача 3. Расчет стержней сжатых внецентренно приложенной силой.

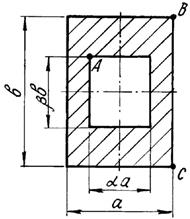
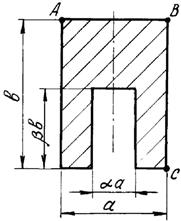
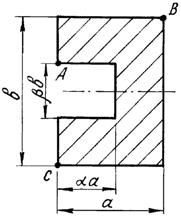
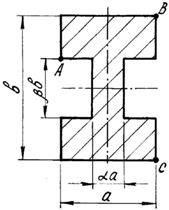
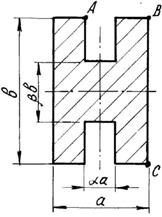
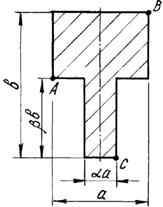
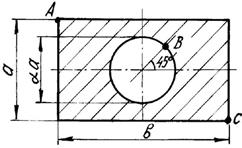
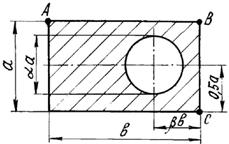
Короткий чугунный брус, поперечное сечение которого показано на рис.3, сжимается силой Р, приложенной в точке А, В или С .

Требуется:

1) вычислить наибольшие растягивающие и сжимающие напряжения в его поперечном сечении, выразив их через величину сжимающей силы Р;

2) из условия прочности бруса найти допускаемую нагрузку Р_д, если заданы пределы прочности для чугуна на растяжение σ_вр и сжатие σ_вс. Запас прочности принять n =1,5.

Числовые данные берутся из табл. 3, схемы поперечных сечений бруса – на рис.3.

Таблица 3

Номер строки	Схема по рис. 3	Размер, м		Коэффициент		Точка приложения силы	Предел прочности, МПа
		а	b	α	β		σвр	σвс
01	1	0,10	0,12	0,3	0,8	A	120	500
02	2	0,12	0,10	0,4	0,5	B	380	1400
03	3	0,06	0,14	0,5	0,6	C	380	1400
04	4	0,06	0,16	0,6	0,8	A	280	1000
05	5	0,08	0,10	0,3	0,5	B	280	1000
06	6	0,08	0,16	0,4	0,6	C	120	500
07	7	0,10	0,12	0,5	0,7	A	120	500
08	8	0,10	0,14	0,6	0,8	B	280	1000
09	9	0,12	0,16	0,3	0,6	C	380	1400
10	10	0,12	0,20	0,5	0,5	A	380	1400
	з	ж	а	б	в	г	д	д

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

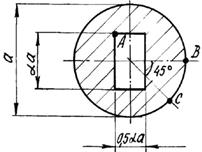
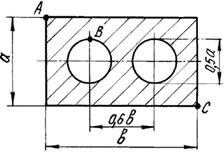
Рис. 3

Задача 4. Расчет стержней сжатых внецентренно приложенной силой.

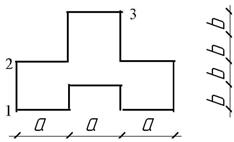
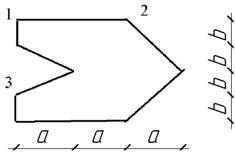
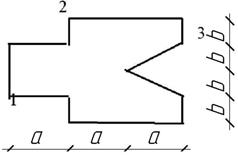
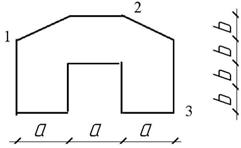
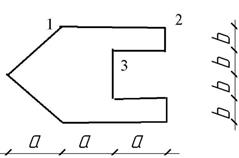
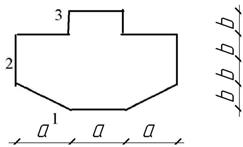
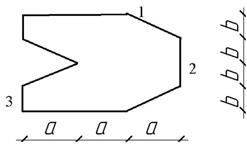
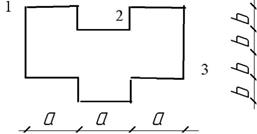
Жесткая колонна заданного поперечного сечения (рис. 4) сжимается силой F , параллельной оси колонны и приложенной в точке, показанной на схеме сечения. Расчетное сопротивление материала на растяжение R_t = 3 МПа, на сжатие R_с = 30 МПа.

Требуется:

1. Найти положение нулевой линии.

2. Вычислить наибольшие сжимающие и растягивающие напряжения и построить эпюру напряжений. Дать заключение о прочности колонны.

3. Определить расчетную несущую способность (расчетную нагрузку) F_max при заданных размерах сечения.

4. Построить ядро сечения.

Числовые данные – в табл. 4.

Таблица 4

Номер строки	Схема по рис.4	Нагрузки F, кН	Размеры сечения, см		Точка приложения силы
			а	b
1	1	120	24	10	1
2	2	160	30	12	2
3	3	180	32	20	3
4	4	200	40	16	1
5	5	240	36	14	2
6	6	280	28	20	3
7	7	140	32	18	3
8	8	220	24	16	2
9	9	260	30	15	1
0	10	240	40	18	2
	д	е	в	г	б

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

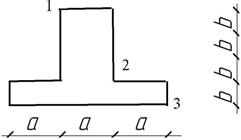
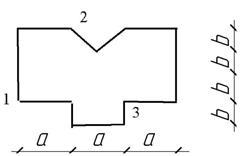
Рис. 4

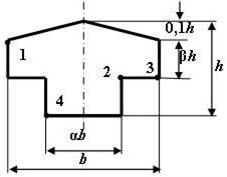
Задача 5. Определение грузоподъемности внецентренно-сжатого чугунного стержня большой жесткости

Исходные данные к задаче принимаются по табл. 5 и схемам на рис. 5.

1. Нарисуйте в аксонометрии призматический стержень, имеющий форму поперечного сечения, показанную на рис. 5. Загрузите стержень растягивающей F_р и сжимающей F_с силами.

2. Найдите геометрические характеристики поперечного сечения стержня. Для этого:

- нарисуйте в масштабе поперечное сечение стержня;

- определите положение центра тяжести;

- проведите главные центральные оси сечения и найдите моменты инерции относительно этих осей.

3. Определите внутренние усилия в произвольном сечении стержня.

4. В опасном сечении найдите положение опасных точек. Для этого запишите уравнение нейтральной линии, постройте ее и найдите точки наиболее удаленные от нейтральной линии. Постройте эпюру напряжений.

5. Из условия прочности в опасных точках найдите допускаемое значение нагрузки (F_р или F_с).

6. Постройте ядро сечения и эллипс инерции.

Таблица 5

Номер строки	b, см	β	Форма сечения по рис. 5	h, см	α	Fс/Fр	Точка приложения силы
							Fр	Fс
01	10	0,4	0	10	0,3	10	1	2
02	5	0,3	1	9	0,4	5	2	3
03	6	0,4	2	8	0,5	3	3	4
04	7	0,5	3	7	0,5	2	4	1
05	8	0,6	4	6	0,6	12	1	3
06	9	0,7	5	5	0,7	0,8	2	4
07	10	0,3	6	12	0,3	0,5	3	1
08	7	0,7	7	10	0,4	0,2	4	2
09	8	0,6	8	6	0,5	0,1	1	4
10	9	0,5	9	7	0,6	4	4	3
	б	в	а	г	б	в	а	г

1 схема 2 схема

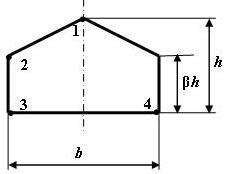
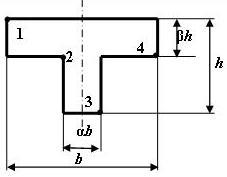
3 схема 4 схема

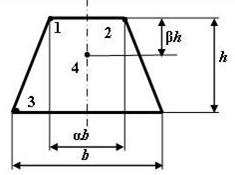
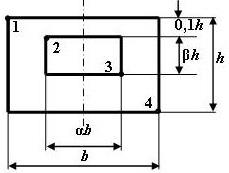
5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

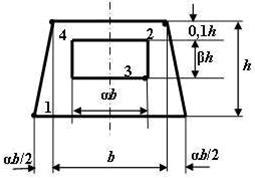
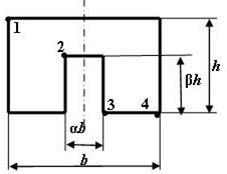
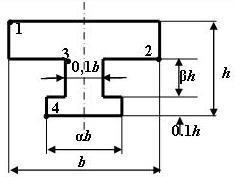
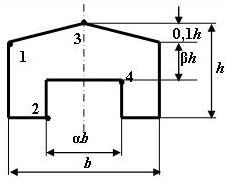
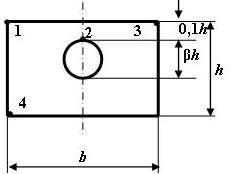
Рис. 5

Задача 6. Определение грузоподъемности внецентренно-сжатого призматического стержня массивного несимметричного сечения

Исходные данные к задаче принимаются по табл. 6 и схемам на рис. 6.

1. Нарисуйте поперечное сечение стержня в масштабе и найдите его геометрические характеристики:

- определите положение центра тяжести;

- проведите через центр тяжести произвольные ортогональные оси координат и найдите осевые и центробежный моменты инерции относительно этих осей;

- вычислите угол, на который надо повернуть оси, чтобы они оказались главными, проведите эти оси на рисунке;

- сосчитайте моменты инерции относительно главных центральных осей и выясните, относительно какой оси момент инерции максимален;

- постройте эллипс инерции.

2. Найдите внутренние усилия, возникающие в произвольном сечении стержня, от сжимающей силы F, приложенной в заданной точке поперечного сечения. (Координаты точки приложения силы в главной центральной системе координат допускается определять по масштабу.)

3. Для определения положения опасных точек запишите уравнение нейтральной линии, постройте ее в масштабе. Найдите положение опасных точек (точек, наиболее удаленных от нейтральной линии), построив эпюру напряжений.

4. Вычислите напряжения в опасных точках, выразив их через F. Из условия прочности в точке с максимальными растягивающими напряжениями найдите значение допускаемой нагрузки F. Если максимальные сжимающие напряжения по модулю больше максимальных растягивающих (см. эпюру напряжений), то проверьте условие прочности в точке с наибольшими сжимающими напряжениями. Если оно не выполняется, определите новое значение допускаемой нагрузки.

5. Постройте ядро сечения. (Координаты полюсов в главной центральной системе координат допускается определять по масштабу.)

6. Нарисуйте эллипс инерции.

Таблица 6

Номер строки	Схема по рис. 6	h, см	α	b, см	β	Точка приложения силы	Допускаемые напряжения, МПа
							на растяжение	На сжатие
01	1	50	0,7	100	0,6	1	1	10
02	2	60	0,6	90	0,5	2	2	20
03	3	70	0,7	80	0,4	3	3	30
04	4	80	0,6	70	0,3	4	4	40
05	5	90	0,5	60	0,5	5	5	50
06	6	100	0,4	50	0,8	1	6	50
07	7	80	0,8	100	0,7	2	5	40
08	8	60	0,7	60	0,6	3	4	30
09	9	50	0,6	80	0,5	4	3	20
10	10	100	0,5	50	0,4	5	2	15
	г	а	б	в	г	а	б	в

1 схема 2 схема

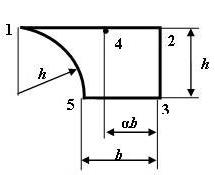
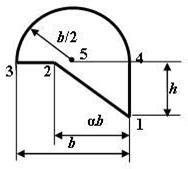
3 схема 4 схема

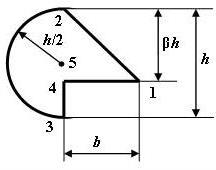
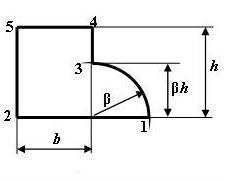
5 схема 6 схема

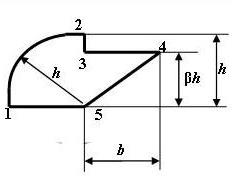
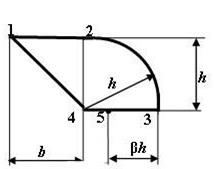
7 схема 8 схема

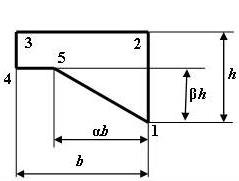
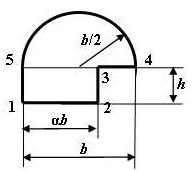
9 схема 10 схема

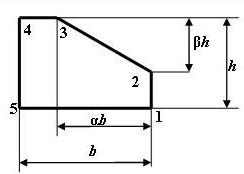
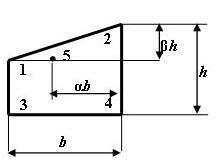
Рис. 6

Задача 7. Определение грузоподъемности внецентренно-сжатого стержня несимметричного сечения из прокатных профилей

Исходные данные к задаче принимаются по табл. 7 и схемам на рис. 7.

Порядок решения задачи тот же, что и в задаче №6. Допускаемое значение нагрузки найдите из условия прочности точки с максимальными по модулю напряжениями. Характеристики прочности примите для стали.

Таблица 7

Номер строки	Схема по рис.7	№ двутавра	№ швеллера	Уголок, мм	Полоса, мм	Точка приложения силы
01	1	20	22	90x8	240x10	1
02	2	22	24	100x7	250x10	2
03	3	24	27	100x12	300x8	3
04	4	27	18	110x7	300x10	4
05	5	18	20	110x8	300x12	5
06	6	20	24	125x8	350x8	1
07	7	22	27	125x12	350x10	2
08	8	24	18	90x7	200x2	3
09	9	27	27	100x8	250x12	4
10	10	18	24	125x10	320x10	5
	а	в	г	б	а	г

1 схема 2 схема

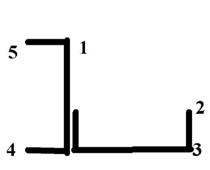
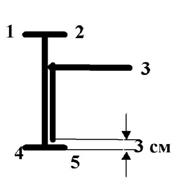
3 схема 4 схема

5 схема 6 схема

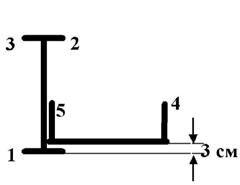
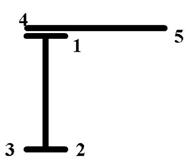
7 схема 8 схема

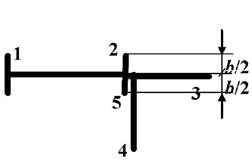
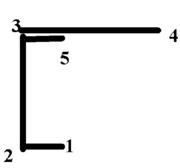
9 схема 10 схема

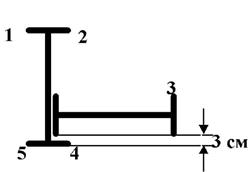
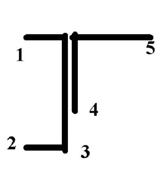
Рис. 7

Задача 8. Определение грузоподъемности внецентренно-сжатого стержня симметричного сечения из прокатных профилей

Консольный стержень большой жесткости имеет поперечное сечение, изображенное на рис. 8. Стержень нагружен сжимающей (приложенной в точке А) или растягивающей (приложенной в точке В) силой F.

Требуется:

1) определить положение главных центральных осей поперечного сечения и величин соответствующих моментов инерции. Вычертить на отдельной странице сечение в масштабе 1:2 и показать внутренние силовые факторы;

2) найти положение нейтральной линии и показать ее на чертеже. Изобразить эпюру напряжений в сечении;

3) из условия прочности по наибольшим напряжениям найти допустимую величину силы F, если [σ]=160 МПа.

Исходные данные к задаче принимаются по табл. 8, таблицам сортамента и схемам на рис. 8.

Таблица 8

Номер строки	Схема по рис.8	XA(B), мм	Y A(B), мм	№ двутавра или швеллера	Равнополочный уголок
01	I	20	30	12	–
02	II	30	35	14	–
03	III	35	40	16	–
04	IV	40	45	18	40×40×5
05	V	45	50	18а	–
06	VI	50	55	20	36×36×4
07	VII	55	60	20а	45×45×5
08	VIII	60	65	22	–
09	IX	65	70	22а	25×25×4
10	X	70	75	24	–
	а	г	а	в	б

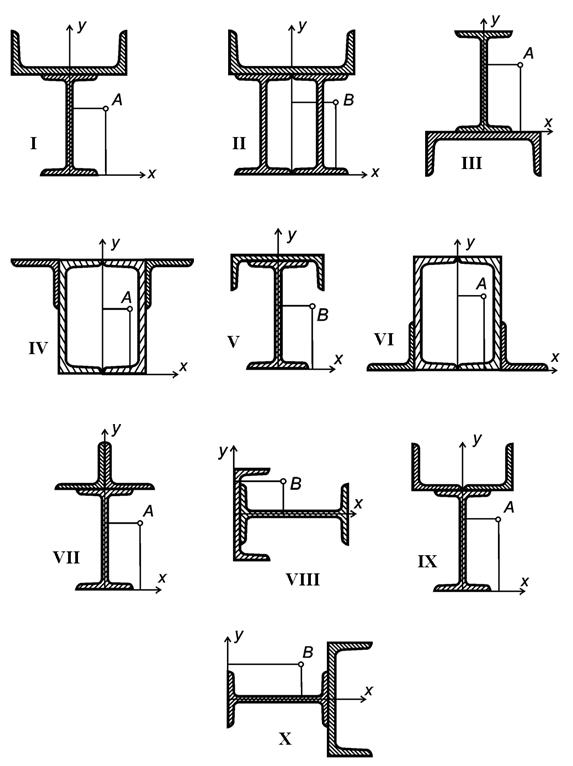
Рис.8

Задача 9. Определение грузоподъемности внецентренно-сжатого стержня несимметричного сечения из прокатных профилей

Короткий чугунный стержень сжимается продольной силой F, приложенной в точке А (рис.9).

Требуется:

1) проверить условие прочности стержня, если допускаемые напряжения при сжатии =100 Мпа, а при растяжении =30 Мпа.

2) определить положение нейтральной оси и построить эпюру σ, приняв за базу перпендикуляр к нейтральной оси.

Исходные данные к задаче принимаются по табл. 9 и схемам на рис. 9.

Таблица 9

Номер строки	Схема по рис.9	n, см	k, см	F, кН	МПа	МПа
01	1	4	6	200	180	60
02	2	5	7	250	200	70
03	3	6	8	300	160	50
04	4	7	4	350	220	80
05	5	8	5	400	160	20
06	6	4	6	200	180	60
07	7	5	7	250	200	70
08	8	6	8	300	160	50
09	9	7	4	350	220	80
10	0	8	5	400	160	20
	б	г	а	в	б	в

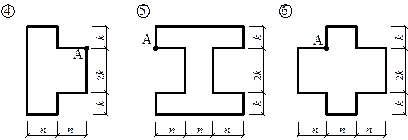
Рис.9

Примеры выполнения задач

Пример 1

Короткий чугунный брус с заданным поперечным сечением (рис.10) сжимается силой Р, приложенной в точке D.

Определить из условия прочности бруса допускаемое значение силы Р_д.

Дано: a = 0,08 м; b = 0,12 м; 𝛼 = 0,5; пределы прочности чугуна при растяжении σ_вр = 280 МПа, при сжатии 𝜎_вс= 1000 МПа; запас прочности принять n =1,5.

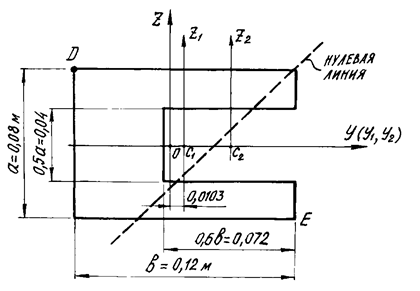
Рис. 10. Поперечное сечение бруса

Решение.

1. Определение геометрических характеристик поперечного сечения.

Заданное сечение (рис.10) рассматриваем как сложное, состоящее из двух прямоугольников: большого сплошного со сторонами a и b и прямоугольного отверстия со сторонами 0,5a и 0,6b.

За исходные координатные оси принимаем оси к z₁ и y. На рис.8 в этой системе координат показаны положения центров тяжести прямоугольников (точки С₁ и С₂) и их главные центральные оси y₁,_,z₁, y₂, z₂. Центр тяжести всего сечения обозначен через O. Он располагается на оси симметрии у, поэтому вычисляется только одна его координата у_C :

где F₁ и F₂ - площади большого прямоугольника и отверстия; y₁ и y₂ - координаты их центров тяжести.

Подсчитываем геометрические характеристики поперечного сечения бруса.

Площади составляющих фигур

F₁=12∙8=96 см²; F₂=4∙7,2=28,8 см².

Площадь сечения всей фигуры:

F = F₁-F₂ = 96-28,8 = 67,2 см² = 67,2∙10^-4 м².

Абсциссы центров тяжести составляющих фигур:

y₁ = 0; y₂ = 2,4 см.

Абсцисса центра тяжести всей фигуры:

Центр тяжести сечения лежит на оси Y (точка О) слева от точки С₁ на расстоянии y_с. Главные центральные оси сечения - Y, Z.

Главные центральные моменты инерции составного сечения относительно осей Y, Z вычисляются с помощью зависимостей между моментами инерции относительно параллельных осей, одна из которых центральная:

Моменты инерции прямоугольников относительно собственных главных центральных осей равны

Расстояния между главными центральными осями Y, Z и собственными главными центральными осями составляющих фигур определяются по чертежу.

Расстояние между главной центральной осью Y и осями y₁,y₂:

a₁ = а₂ = 0, так как главные центральные оси у₁ и y₂ составляющих фигур совпадают с главной центральной осью Y сечения;

расстояния между главной центральной осью Z и осями z₁, z₂:

b₁ = 1,03 см,

b₂ = 1,03 + 2,4 =3,43 см .

Подставив найденные величины в формулы для вычисления главных центральных моментов инерции и учитывая, что осевой момент инерции отверстия условно считается отрицательным, получаем

J_Y = 512-38,4 = 473,6 см⁴ = 473,6∙10^-8 м⁴;

J_Z = (1152+96∙1,03²) – (124,4+28,8∙3,43²) = 790,6 см⁴ = 790,6∙10^-8 м⁴.

Квадраты главных центральных радиусов инерции

2. Определение положения нулевой линии.

По условию задачи сила Р приложена в точке D, координаты которой в системе главных центральных осей Y, Z определяются по рис. 10:

y_P = -(6-1,03) = -4,97 см = -4,97∙10^-2 м;

z_P = 4 см = 4∙10^-2 м.

Отрезки, отсекаемые нулевой линией на осях координат Y, Z:

На осях координат Y, Z откладываются в масштабе величины найденных отрезков и проводится нулевая линия.

3. Вычисление максимальных нормальных напряжений в поперечном сечении бруса.

Максимальные напряжения возникают в точках, наиболее удаленных от нулевой линии. В рассматриваемой задаче это точки D и E. В точке D напряжения сжимающие, в точке E - растягивающие.

Координаты опасных точек находятся по рис. 8:

y* = y_E = 6+1,03 = 7,03 см = 7,03 см = 7,03∙10^-2 м; z* = z_E = -4 см = -4∙10^-2 м;

y** = y_D = -4,97 см = -4,97∙10^-2 м; z** = z_D = 4 см = 4∙10^-2 м.

Максимальные растягивающие и сжимающие напряжения выражаются через внешнюю нагрузку;

Допускаемая нагрузка Р_доп определяется из условий прочности бруса по растягивающим и сжимающим напряжениям.

Допускаемые напряжения определяются по исходным данным для растяжения и для сжатия хрупкого материала, в рассматриваемом случае чугуна:

На растяжение

На сжатие

Из условия прочности материала бруса на растяжение определяется величина допускаемой нагрузки

откуда

Из условия прочности на сжатие

откуда

В качестве допускаемой нагрузки принимается меньшая из двух полученных, что обеспечивает прочность бруса как по растягивающим, так и по сжимающим напряжениям, то есть P_доп=296,4 кН.

Пример 2

Чугунный короткий стержень, поперечное сечение которого изображено на рис. 11, сжимается продольной силой F, приложенной в точке A.

Дано: a=6 см, b=5 см, [σ_c]=60 Мпа, [σ_p]=25 Мпа.

Требуется:

1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив эти напряжения через F и размеры сечения;

2) найти допускаемую нагрузку F при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие [σ_c] и на растяжение [σ_p].

Рис. 11

Решение.

Поперечное сечение имеет одну ось симметрии, которая является главной центральной осью. Сложное сечение представим в виде двух простых фигур, причем вторая, в виде прямоугольного выреза, с отрицательной площадью

A=A₁+A₂=12∙20+(-10∙6)=180 см²=180∙10^-4 м².

Положение центра тяжести сечения относительно оси x₁ (рис. 12):

Здесь y₁ и y₂ расстояния от оси x₁ до центров тяжести простых фигур. Вторая главная центральная ось x пройдет перпендикулярно к оси симметрии y и через найденный центр тяжести сечения. Величины главных центральных моментов инерции сложного сечения:

Здесь a₁ и a₂ - расстояния от главной центральной оси x до центров тяжести простых фигур. Определим внутренние силовые факторы - продольную силу и два изгибающих момента относительно главных центральных осей:

N_z=-F, M_x=F∙0,05 (м), M_y=F∙0,10 (м).

Тогда уравнение нулевой линии, записанное в координатных осях y и x, с учетом знаков напряжений и текущих координат в четверти, принимает следующий вид: σ=0, где

или после приведения подобных членов имеем y + 0,528x - 2,20=0.

Положение нулевой линии показано на рис. 12, из которого видно, что наиболее удаленные точки от нулевой линии в сжатой и растянутой областях будут соответственно точки A и B, т.е. точки в окрестностях которых возникают наибольшие напряжения.

Рис. 12

Наибольшие сжимающие и наибольшие растягивающие напряжения в поперечном сечении будут равны

Допускаемую нагрузку F находим из условий прочности для самых напряженных точек A и B (сжимающие напряжения сравниваем по модулю):

За окончательное значение допускаемой нагрузки принимаем наименьшее из двух определенных выше значений нагрузки: F=98,2 кН.

Пример 3

Короткий стержень (рис.13), нагружен продольной силой F=50 кH, приложенной в точке A. Допускаемое напряжение на растяжение для материала стержня [σ]_р = 30 МПа, на сжатие [σ]_сж = 120 МПа. Численные данные: а=3 см, b=6 см, вид нагружения: сжатие.

Требуется:

1) проверить стержень на прочность;

2) построить эпюру напряжений в сечении.

Замечание: при решении задачи вычертить поперечное сечение стержня в масштабе со всеми размерами, показать точку приложения силы, положение нейтральной линии и опасных точек.

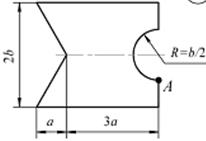
Рис.13

Решение.

1. Разбиваем сложное сечение на конечное число простых сечений.

Прямоугольник 12x12 см. А₁=144 см²

Треугольник 3x12 см. А₂=18см²

Полукруг R=3 см. А₃=14,13 см²

В результате мы получили сложное сечение, состоящее из трех простых: квадрата, треугольника, полукруга.

2. Определяем положение главных центральных осей сечения.

Положение одной главной оси известно (ось симметрии), а вторая, перпендикулярная ей, проходит через центр тяжести сечения. Положение центра тяжести вычисляем по формуле:

где x₁, x₂, x₃, y₁, y₂, y₃ – расстояние от центра тяжести соответствующей фигуры до нулевых осей; А₁, А₂, А₃ – площади соответствующих фигур; А_общ - общая площадь сечения. А_общ =111,87 см.

Таким образом, центр тяжести сечения С в системе начальных координат x₀, y₀ находится в точке с координатами (0; 0,21 см). Через эту точку проводим главные центральные оси x_c, y_c.

3. Определение радиусов инерции сечения.

Для расчета используем следующие формулы:

Определим осевые момента инерции сечения по формулам:

где , , – осевые моменты инерции соответствующих сечений; а₁, а₂, а₃, b₁, b₂, b₃ – координаты отсчитываемые от главных центральных осей до центра тяжести соответствующего элемента: а₁=-0,21 см., а₂=-5,21 см., а₃=4,52 см., b₁=0 см., b₂=0 см., b₃=0 см.

Для квадрата

Для треугольника:

Для полукруга:

Вычисляем осевые моменты инерции:

Квадраты радиусов инерции:

4. Построение нейтральной линии.

Нейтральная линия необходима для определения положения опасных точек. Координаты точек пересечения нейтральной линии с осями сечения x_c, y_c определяются по формулам:

Координаты точки приложения силы в системе главных центральных осей определяются из схемы:

Тогда координаты пересечения нейтральной линии с осями координат равны:

Получаем на главных центральных осях две точки с координатами (-2,25; 0) и (0; 2,8).Соединяем их прямой линией, которая является нейтральной линией. Зная положение нейтральной линии, можно утверждать, что опасными точками в сечении будут точки С и В, т. к. они наиболее удалены от этой линии. Нейтральная линия делит сечение на две области: область сжатия и область растяжения. При этом в точке С будут действовать максимальные сжимающие напряжения, а в точке В - максимальные растягивающие напряжения.

5. Проверка прочности.

Определим напряжения в опасных точках по формуле:

Заключение: На основе проведенного проверочного расчета короткого стержня при внецентренном сжатии можно сделать заключение, что рассматриваемый стержень не разрушится под действием приложенной нагрузки, т. к. одновременно выполняются условия прочности по сжатым и растянутым волокнам.

Пример 4

Короткий чугунный стержень сжимается продольной силой F, приложенной в точке А (рис.14).

Требуется:

1) проверить условие прочности стержня, если допускаемые напряжения при сжатии =100 Мпа, а при растяжении =30 Мпа.

2) определить положение нейтральной оси и построить эпюру σ, приняв за базу перпендикуляр к нейтральной оси.

Дано: F = 200 кН; a = b = 4 см.

Рис.14

Решение.

Поскольку в формулу для определения напряжений при внецентренном растяжении-сжатии входят геометрические характеристики сечения и координаты точек сечения в системе главных центральных осей инерции, то в первую очередь следует найти положение этих осей.

Сечение (рис. 14) имеет горизонтальную ось симметрии z_o, которая и является одной из главных центральных осей инерции.

Проведем ось y вертикально, так, чтобы все сечение располагалось справа от нее. Представим сплошное сечение вертикальным прямоугольником площадью А=4×16=64 см² и двумя горизонтальными, площадью А=12×4 = 48 см², каждый. Центры тяжести прямоугольников удалены от оси у на расстоянии z = 2 и z =10 см, соответственно. Координата центра тяжести сложного сечения:

а общая площадь сечения (ΣA_i) равна 160 см².

Таким образом, определена другая главная центральная ось инерции y_o, (см. рис.14). Моменты инерции сечения относительно этих осей:

где - расстояния центров тяжести прямоугольников до осей y_o и z_o соответственно.

Изгибающие моменты, входящие в формулу для определения напряжения, создаются сжимающей силой F = -200 кН, которая приложена в точке А с координатами [9,2; -4], тогда:

Наибольшие значения напряжений в растянутой и сжатой зонах можно вычислить, если известны координаты «опасных» точек. Эти точки наиболее удалённые от нейтральной оси, положение которой определяется отрезками у_о, z_o, отсекаемыми ею на осях координат. При этом:

Квадраты радиусов инерции равны

Итак,

Проведя нейтральную ось (н.о. на рис.14), находим наиболее удаленные от нее точки С (-6,8; 8) и Д (9,2; -8).

Определим напряжения в этих точках:

На перпендикулярах к базовой линии отложим в масштабе значения напряжений для точек С и Д и, соединив эти точки прямой линией, построим эпюру σ. Используя эту эпюру легко определить напряжения в любой точке сечения. Для этого достаточно восстановить перпендикуляр к базовой линии из этой точки (например, из точки А), измерить отрезок nn и, зная масштаб построения эпюры, определить величину напряжения в точке.

Условие безопасной прочности в сжатой зоне выполняется, т.к. |-712|<|-100| МПа, а условие прочности в растянутой зоне , не выполняется, т.к. 34,3 мПа больше допускаемого напряжения (30 МПа) и перегрузка , не допустима.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00