Расчетно-графические работы

 

 

Главная

 

Задача 1. Расчет коленчатого вала на изгиб с кручением

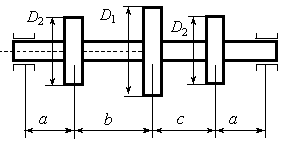
Исходные данные к задаче принимаются по табл. 1 и схеме на рис. 1.

1. Определите опорные реакции. Закрепление коленчатого вала, показанного на рис. 1, следует принять следующим: оба конца имеют шарнирное закрепление в плоскости, перпендикулярной оси стержня, правый конец, помимо этого, имеет жесткое закрепление от продольных перемещений и от поворота сечения в плоскости, перпендикулярной оси стержня.

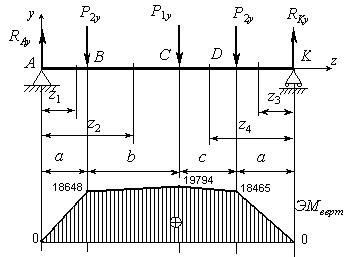
2. Определите внутренние усилия (продольную и поперечные силы, изгибающие и крутящий моменты), действующие в сечениях элементов вала. Постройте эпюры внутренних усилий.

3. Подберите предварительно размер круглого поперечного сечения шатунной шейки (стержень 1) из условия статической прочности, учитывая только действие изгиба и кручения по приведенным моментам при пониженных допускаемых напряжениях [σ] = 95 МПа.

4. Подберите предварительно размеры прямоугольного поперечного сечения кривошипа (стержень 2) из условия статической прочности при пониженных допускаемых напряжениях [σ] = 95 МПа, учитывая в первом приближении только изгибающие моменты. Сечение должно быть расположено выгодным образом по отношению к силовым плоскостям. Отношение высоты к ширине сечения h/b задано в табл. 1.

5. Постройте эпюры нормальных и касательных напряжений в опасных сечениях шатунной шейки и кривошипа, принимая во внимание все факторы. Для стержня круглого сечения допускается пренебречь действием поперечных сил.

6. Определите амплитуду и среднее напряжение цикла для максимальных нормальных и касательных напряжений в сечении шатунной шейки, считая, что σ изменяются по симметричному циклу, а τ - по отнулевому. Вычислите действительный коэффициент запаса усталостной прочности при совместном действии кручения и изгиба и сравните его с допускаемым значением n =1,5.

7. При невыполнении условия усталостной прочности измените размер поперечного сечения шейки и повторите расчет.

8. Проверьте статическую прочность шейки в опасной точке с учетом действия продольной силы на повышенное действие нагрузки при коэффициенте перегрузки 2,0. Если условия прочности не будут выполнены, измените размеры сечения шейки.

9. Проверьте статическую прочность прямоугольного сечения кривошипа в опасных точках с учетом всех действующих усилий при коэффициенте перегрузки 2,0. Если условия прочности не будут выполнены, измените размеры сечения кривошипа.

Примечание. Для проверки статической прочности в пп. 8, 9 примите значение допускаемого напряжения равным 190 МПа.

Общие данные для всех вариантов:

σ-1 = 200 МПа, τ-1 = 100 МПа - пределы выносливости при изгибе и кручении для симметричного цикла;

ψσ = 0,1, ψτ = 0,05 - коэффициенты, учитывающие влияние среднего напряжения цикла на сопротивление усталости;

Kd = 0,8 - масштабный фактор; KF= 0,9 - фактор шероховатости поверхности; Kσ и Kτ - эффективные коэффициенты концентрации напряжений (заданы в таблице 1 условно).

 

Таблица 1

Номер

строки

F1,

кН

F2,

кН

F3,

кН

M,

кНм

a,

см

b,

см

c,

см

α

Kσ

Kτ

h/b

01

1,5

6

2

1,2

10

14

16

0,4

1,7

1,25

1

02

2

5

1

0,8

12

12

24

0,5

1,8

1,35

1,5

03

2,5

4

1,5

0,6

14

10

30

0,6

1,9

1,4

2

04

3

5

1

1,0

8

16

18

0,4

1,9

1,4

2,5

05

3,5

6

2

0,8

10

14

22

0,5

1,8

1,35

3

06

3

7

1,5

0,6

12

12

16

0,6

1,7

1,25

2,5

07

2,5

8

2,5

1,0

14

10

14

0,4

1,7

1,25

2

08

2

9

1

1,2

8

16

12

0,5

1,8

1,35

1,5

09

1,5

6

2

0,6

10

10

22

0,6

1,9

1,4

1

10

3

5

1,5

0,8

12

8

20

0,5

1,7

1,25

2

 

а

б

в

г

а

б

в

г

а

б

г

 

Рис. 1

 

 

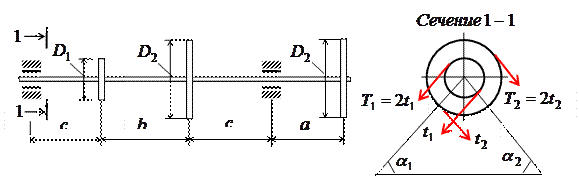
Задача 2. Расчет вала на совместное действие кручения и изгиба

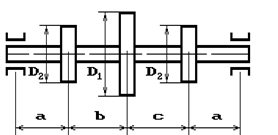
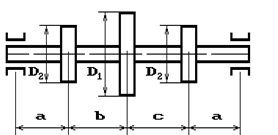
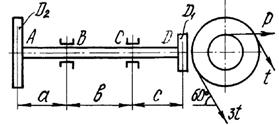
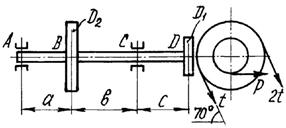
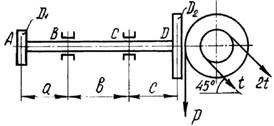
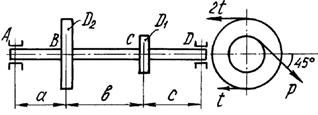
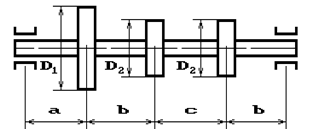
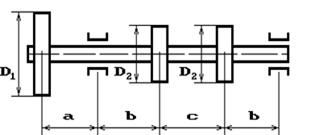
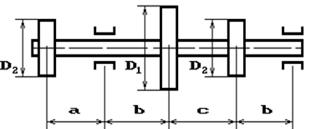
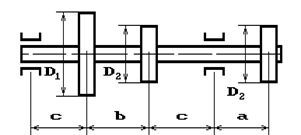
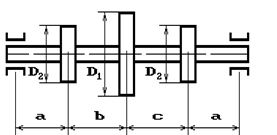
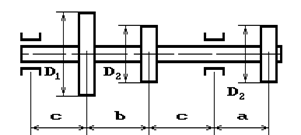
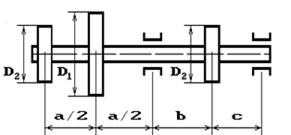
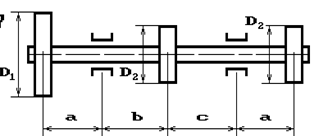
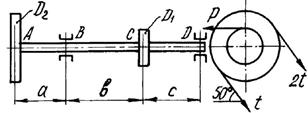
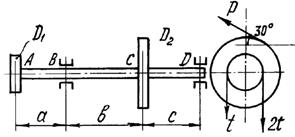
Шкив с диаметром D1 и углом наклона ветвей ремня к горизонту α1 делает n оборотов в минуту и передает мощность N кВт. Два других шкива имеют одинаковый диаметр D2 и одинаковые углы наклона ветвей к горизонту α2 и каждый из них передает мощность 0,5N (рис.2). Требуется:

1) определить моменты, приложенные к шкивам, по заданным величинам N и n;

2) построить эпюру крутящих моментов Мкр;

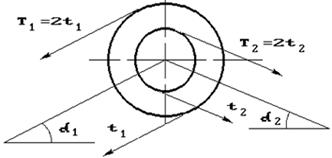
3) определить окружные усилия t1 и t2, действующие на шкивы, по найденным моментам и заданным диаметрам шкивов D1 и D2;

4) определить давления на вал, принимая их равными трем окружным усилиям;

5) определить силы, изгибающие вал в горизонтальной и вертикальной плоскостях (вес шкивов и вала не учитывать);

6) построить эпюры изгибающих моментов от горизонтальных (Мгор) и вертикальных (Мверт) сил;

7) построить эпюру суммарных изгибающих моментов, пользуясь формулой

8) при помощи эпюр Мкр и Мизг найти опасное сечение и определить величину максимального расчетного момента (по четвертой теории прочности);

9) подобрать диаметр вала d при [σ] =70 МПа и округлить его величину.

Данные взять из табл. 2.

Таблица 2

Номер

cтроки

Схема

по рис.2

N,

кВт

n,

об/мин

a,

м

b,

м

c,

м

D1,

м

D2,

м

α1

α2

01

1

10

100

1,1

1,1

1,1

1,1

1,1

10о

10о

02

2

20

200

1,2

1,2

1,2

1,2

1,2

20о

20о

03

3

30

300

1,3

1,3

1,3

1,3

1,3

30о

30о

04

4

40

400

1,4

1,4

1,4

1,4

1,4

40о

40о

05

5

50

500

1,5

1,5

1,5

1,5

1,5

50о

50о

06

6

60

600

1,6

1,6

1,6

0,6

0,6

60о

60о

07

7

70

700

1,7

1,7

1,7

0,7

0,7

70о

70о

08

8

80

800

1,8

1,8

1,8

0,8

0,8

80о

80о

09

9

90

900

1,9

1,9

1,9

0,9

0,9

90о

90о

10

10

100

1000

1,0

1,0

1,0

1,0

1,0

0о

0о

11

11

30

100

1,3

1,3

1,2

1,5

1,2

20о

30о

12

12

40

200

1,4

1,4

1,3

0,6

1,3

30о

40о

13

13

50

300

1,5

1,5

1,4

0,7

1,4

40о

50о

14

14

60

400

1,6

1,6

1,5

0,8

1,5

50о

60о

15

15

70

500

1,7

1,7

1,6

0,8

0,6

60о

40о

16

16

80

600

1,8

1,8

1,7

0,9

0,7

70о

50о

17

17

10

700

1,1

1,9

1,8

1,0

0,8

80о

60о

18

18

20

800

1,2

1,1

1,1

1,5

0,9

10о

70о

19

19

30

900

1,3

1,2

1,2

0,6

1,1

20о

80о

20

20

40

1000

1,4

1,3

1,3

0,7

1,2

30о

90о

21

21

50

100

1,5

1,4

1,4

0,8

1,3

40о

0о

22

22

60

200

1,6

1,5

1,5

1,1

1,4

50о

30о

23

23

30

400

1,7

1,6

1,6

1,2

1,5

60о

40о

24

24

40

500

1,8

1,7

1,7

1,3

0,6

70о

50о

25

25

50

600

1,9

1,8

1,8

1,4

0,7

80о

60о

26

26

60

700

1,0

1,9

1,9

1,5

0,8

90о

80о

27

27

70

800

1,3

1,0

1,0

0,6

0,9

0о

90о

28

28

80

900

1,4

1,3

1,2

0,7

1,0

20о

0о

29

29

90

1000

1,5

1,4

1,3

0,8

1,2

30о

30о

30

30

100

100

1,6

1,5

1,4

0,8

1,3

40о

40о

31

31

30

200

1,7

1,6

1,5

1,1

1,4

50о

50о

32

32

40

300

1,8

1,7

1,7

1,2

1,5

60о

60о

33

33

50

300

1,7

1,8

1,8

1,3

0,6

70о

80о

34

34

60

400

1,8

1,9

1,9

1,4

0,7

80о

90о

35

35

100

500

1,1

1,4

1,0

1,5

0,8

0о

0о

36

36

30

600

1,2

1,0

1,2

1,2

0,9

20о

30о

 

б

в

а

б

г

а

в

б

г

в

 

image003

 

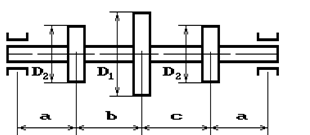
1 схема                                                                         2 схема

image129image130

 

3 схема                                                                        4 схема

image003image004

 

5 схема                                                                    6 схема

image133   image129

 

7 схема                                                                   8 схема

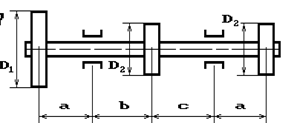
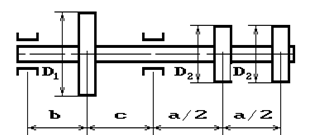
image135image136

 

9 схема                                                                   10 схема

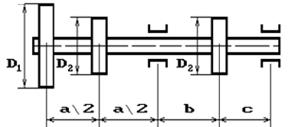
image090image091

 

11 схема                                                          12 схема

image129image130

 

13 схема                                                                    14 схема

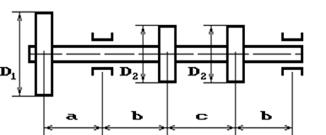
image003image004

 

15 схема                                                              16 схема

image133image091

 

17 схема                                                                   18 схема

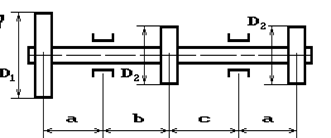
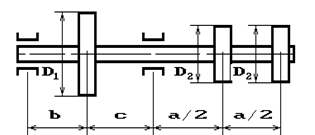
image135image136

 

19 схема                                                                   20 схема

image090image091

 

21 схема                                                                         22 схема

image129image130

 

23 схема                                                                       24 схема

image003image004

 

25 схема                                                               26 схема

image133image090

 

27 схема                                                                   28 схема

image135image136

 

29 схема                                                                   30 схема

image090image091

 

31 схема                                                                     32 схема

image129image130

 

33 схема                                                                            34 схема

image003image004

 

35 схема                                                                36 схема

image133image090

 Рис. 2

 

 

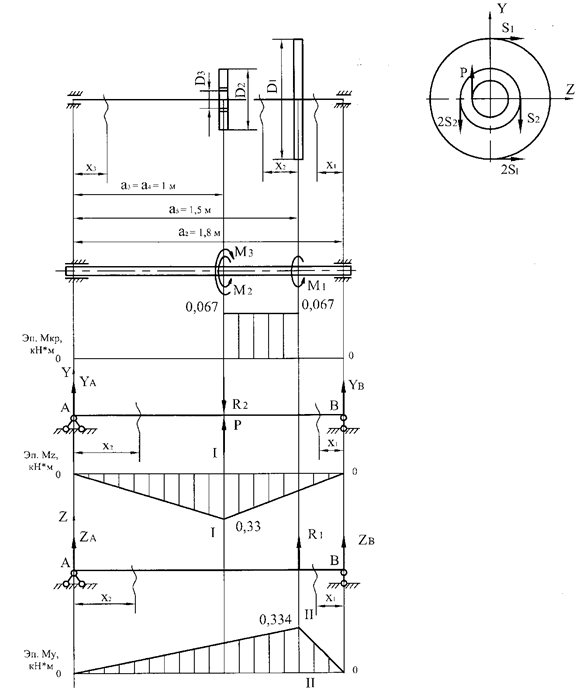
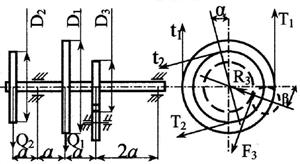
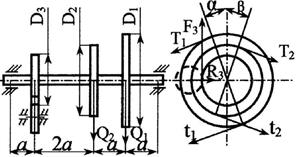
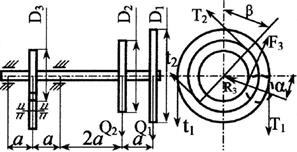
Задача 3. Расчет вала на совместное действие кручения и изгиба

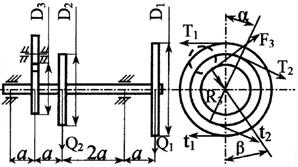
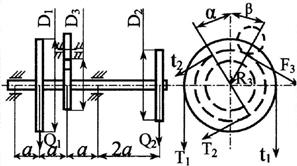
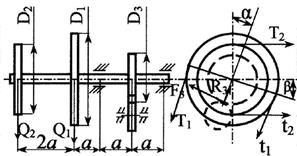
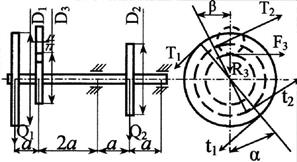
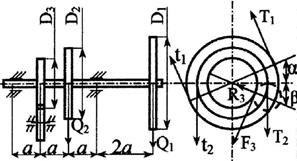
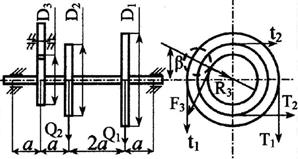
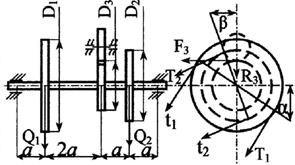
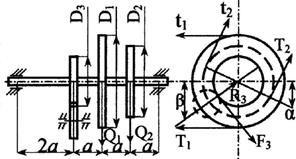
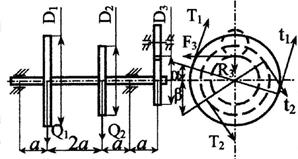
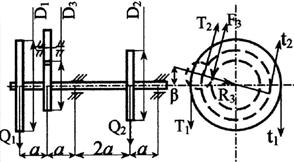
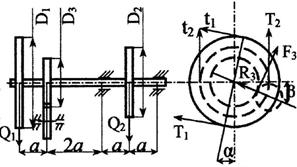
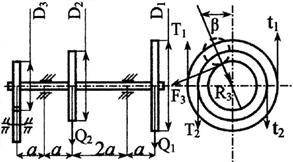
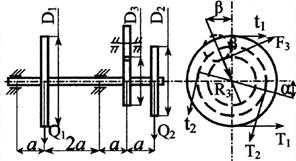
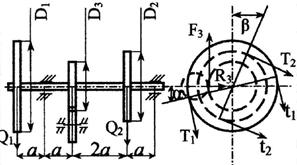
Стальной вал делает n оборотов в минуту, шкив с диаметром D1 передает мощность N1 кВт, шкив с диаметром D2 передает мощность N2 кВт. Мощность, передаваемую шестерней с диаметром D3, найти из условия равновесия вала. Требуется:

1. Определить крутящие моменты по заданным величинам мощностей – N,  кВт и числе оборотов – n, об/мин, приняв ведущим шкив D1.

2. Построить эпюру крутящих моментов.

3. Определить силы, действующие на вал в горизонтальной и вертикальной плоскостях, приняв в ременной передаче Т≅2t, а в зубчатой R≅0,3F.

4. Построить эпюры изгибающих моментов от сил, действующих на вал в горизонтальной и вертикальной плоскостях.

5. Построить суммарную эпюру изгибающих моментов.

6. Найти опасное сечение вала и определить величину расчетного момента в этом сечении по третьей и четвертой теориям прочности (для сравнения).

7. Подобрать диаметр вала при [σ]= 80 МПа и округлить его величину до ближайшей большей из стандартного ряда.

Примечания:

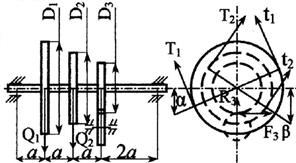
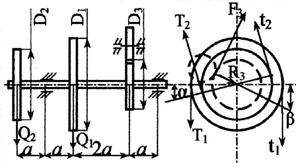
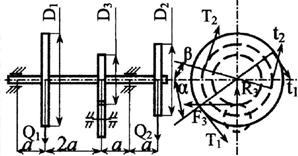
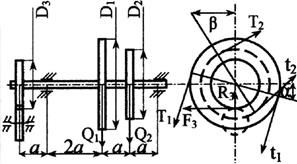
1. Исходные данные  взять в табл. 3 и на рис. 3

2. Если на схеме вала не показаны углы α и β, направление сил принимается по схеме (вертикальным или горизонтальным).

3. В число выполненных чертежей должно входить:

а) схема вала с нанесением размеров и нагрузок;

б) эпюра крутящих моментов;

в) эпюра изгибающих моментов в вертикальной и  горизонтальной плоскостях;

г) суммарная эпюра изгибающих моментов.

4. Эпюры должны быть вычерчены в масштабе с нанесением значений характерных ординат.

 

Таблица 3

Номер

строки

Схема

по рис.3

Числовые значения вариантов

N1

кВт

N2

кВт

n,

об/мин

D1,

м

D2,

м

D3,

м

Q1,

кН

Q2,

кН

a,

м

α

β

01

1

6

3

200

0,80

0,40

0,10

100

60

0,40

20

45

02

2

7

3

150

0,70

0,35

0,10

80

40

0,50

30

20

03

3

9

4

300

1,00

0,32

0,08

90

50

0,50

45

15

04

4

11

3

400

0,90

0,50

0,12

80

50

0,40

45

30

05

5

12

6

340

0,65

0,40

0,09

70

30

0,70

35

30

06

6

14

6

450

0,70

0,35

0,07

75

40

0,30

25

30

07

7

8

3

500

0,85

0,30

0,09

70

25

0,50

40

50

08

8

16

10

440

0,60

0,45

0,08

65

40

0,40

50

40

09

9

12

4

600

0,90

0,35

0,02

85

35

0,30

60

70

10

10

19

11

700

0,62

0,40

0,10

60

20

0,60

80

60

11

11

9

6

200

0,85

0,40

0,07

80

30

0,50

75

15

12

12

21

9

1400

0,70

0,38

0,03

70

40

0,70

15

75

13

13

22

9

300

1,00

0,36

0,09

95

60

0,40

60

75

14

14

21

8

1200

0,90

0,42

0,10

75

35

0,65

25

45

15

15

19

7

500

0,85

0,30

0,15

100

30

0,30

30

60

16

16

33

16

1500

0,65

0,36

0,12

90

25

0,30

25

60

17

17

26

14

250

0,75

0,45

0,14

80

40

0,40

45

15

18

18

24

10

800

0,80

0,35

0,08

70

20

0,50

15

30

19

19

30

18

700

0,90

0,40

0,09

65

30

0,70

30

45

20

20

29

19

1000

0,60

0,30

0,70

85

45

0,60

45

80

21

21

8

3

800

0,85

0,35

0,10

90

30

0,30

20

70

22

22

11

6

500

0,60

0,45

0,15

85

45

0,40

25

65

23

23

9

3

300

0,80

0,30

0,12

80

30

0,50

30

45

24

24

12

6

900

0,75

0,35

0,14

60

20

0,60

35

60

25

25

15

10

100

1,00

0,42

0,12

75

40

0,20

40

50

26

26

12

4

1200

0,70

0,50

0,15

70

30

0,50

50

40

27

27

10

2

400

0,80

0,45

0,10

65

35

0,30

60

35

28

28

18

8

300

0,63

0,32

0,11

100

60

0,60

45

30

29

29

9

7

400

1,00

0,40

0,90

90

40

0,40

65

25

30

30

11

6

800

0,80

0,45

0,10

95

50

0,70

70

20

 

а

г

в

б

а

г

в

б

а

г

в

б

 

1 схема                                                                    2 схема

1   2

 

 

3 схема                                                                     4 схема

3   4

 

 

5 схема                                                                     6 схема

5   6

 

 

7 схема                                                                         8 схема

7   8

 

 

9 схема                                                                      10 схема

9   10

 

 

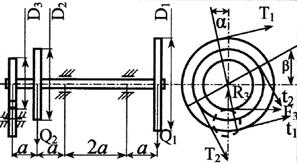
11 схема                                                                           12 схема

1   2

 

 

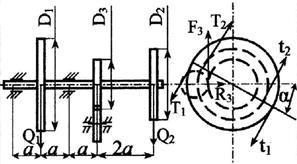
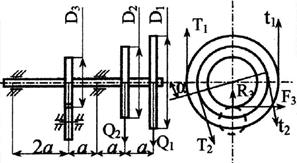
13 схема                                                                           14 схема

3   4

 

 

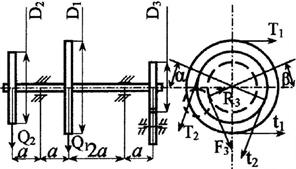
15 схема                                                                           16 схема

5   6

 

 

17 схема                                                                          18 схема

7   8

 

 

19 схем                                                                            20 схема

9   10

 

 

21 схема                                                                             22 схема

1   2

 

 

23 схема                                                                             24 схема

3   4

 

 

25 схема                                                                           26 схема

5   6

 

 

27 схема                                                                            28 схема

7   8

 

 

29 схема                                                                       30 схема

9   10

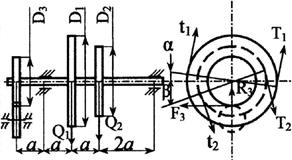
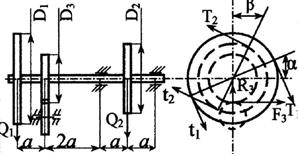
Рис. 3

 

 

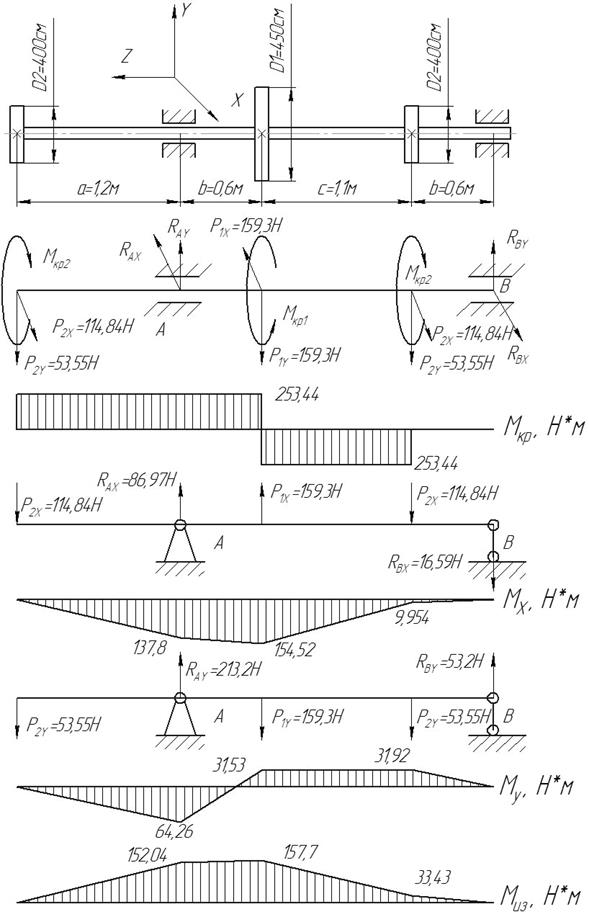
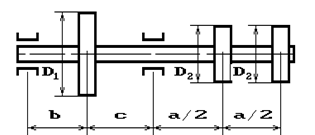
Задача 4. Расчет вала редуктора на совместное действие кручения и изгиба и растяжения-сжатия

Для заданной расчетной схемы вала при указанных размерах и нагрузках требуется:

1. Построить эпюры изгибающих моментов в горизонтальной и вертикальной плоскостях.

2. Построить суммарную эпюру изгибающих моментов.

3. Построить эпюру продольных сил.

4. Построить эпюру крутящих моментов.

5. Найти опасное сечение, используя 4-ую теорию прочности, подобрать диаметр вала d и округлить его величину до ближайшей большей из стандартного ряда.

Примечания:

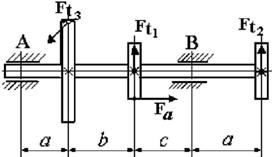
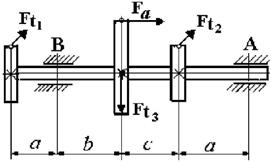
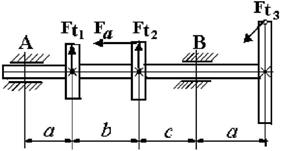
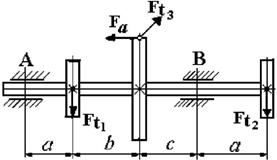
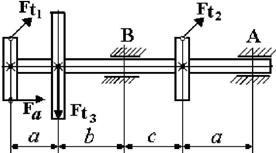
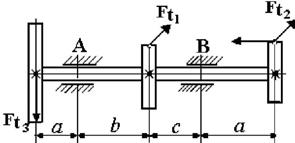
1. Пояснения к схеме вала и характеру нагрузки см. на рисунке 4.1.

2. Диаметры колес I и II равны D1 = D2; диаметр колеса D3 =2D1.

3. Усилие Ft3 определяется из условия равновесия вала; усилие Fa = 0,5Ft1 .

4. Опора А - шарнирная неподвижная, опора В – шарнирная подвижная.

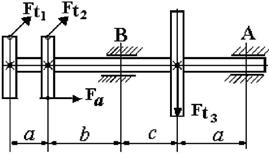
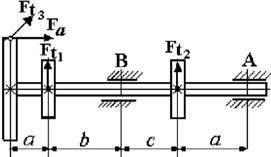
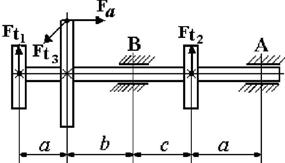
5. Данные для решения задачи взять в табл. 4 и на рис. 4.2.

 

Рис. 4.1

 

Таблица 4

Номер

строки

Схема

по рис. 4.2
Числовые значения вариантов

A,

м

b,

м

с,

м

Ft1,

Н

Ft2,

Н

D1,

м

[σ],

МПа

01

1

0,10

0,15

0,20

30

25

0,10

100

02

2

0,12

0,16

0,18

28

24

0,12

120

03

3

0,14

0,18

0,16

26

23

0,14

110

04

4

0,16

0,20

0,14

25

22

0,16

130

05

5

0,18

0,10

0,12

24

21

0,18

140

06

6

0,20

0,12

0,10

23

20

0,20

150

07

7

0,22

0,14

0,18

22

19

0,22

160

08

8

0,24

0,16

0,20

21

18

0,24

170

09

9

0,26

0,18

0,16

20

17

0,26

180

10

10

0,28

0,20

0,14

27

16

0,28

190

11

11

0,30

0,20

0,28

15

25

0,25

250

12

12

0,29

0,21

0,26

16

24

0,24

245

13

13

0,28

0,22

0,24

17

23

0,23

240

14

14

0,27

0,23

0,22

18

22

0,22

235

15

15

0,26

0,24

0,20

19

21

0,21

230

16

16

0,25

0,25

0,18

20

20

0,20

225

17

17

0,24

0,26

0,16

21

19

0,18

220

18

18

0,23

0,27

0,14

22

18

0,16

215

19

19

0,22

0,28

0,12

23

17

0,14

210

20

20

0,21

0,29

0,10

24

16

0,12

200

21

21

0,20

0,26

0,30

50

35

0,6

200

22

22

0,18

0,28

0,28

49

36

0,8

190

23

23

0,16

0,30

0,26

48

37

0,10

200

24

24

0,14

0,32

0,24

47

38

0,12

180

25

25

0,12

0,34

0,25

46

39

0,14

160

26

26

0,10

0,36

0,22

45

40

0,16

150

27

27

0,15

0,38

0,20

42

41

0,18

140

28

28

0,22

0,24

0,32

41

42

0,20

130

29

29

0,24

0,22

0,34

40

43

0,22

120

30

30

0,26

0,20

0,36

43

44

0,24

110

 

г

в

б

а

г

б

в

а

 

1 схема                                                                   2 схема

1   2

 

 

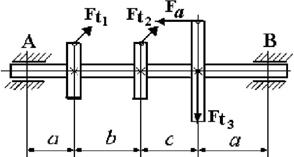
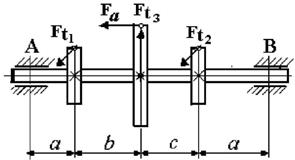
3 схема                                                                   4 схема

3   4

 

 

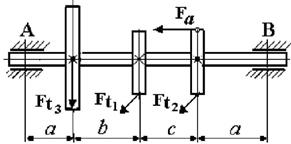
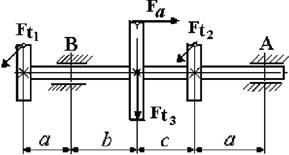
5 схема                                                                     6 схема

5   6

 

 

7 схема                                                                   8 схема

7   8

 

 

9 схема                                                         10 схема

9   10

 

 

11 схема                                                                  12 схема

1   2

 

 

13 схема                                                                   14 схема

3   4

 

 

15 схема                                                                 16 схема

5   6

 

 

17 схема                                                                18 схема

7   8

 

 

19 схема                                                             20 схема

9   10

 

 

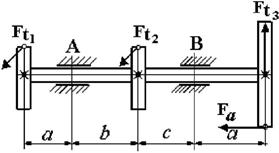
21 схема                                                                22 схема

1   2

 

 

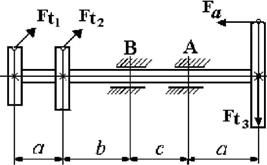
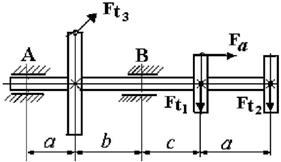
23 схема                                                               24 схема

3   4

 

 

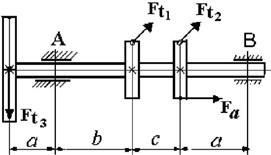
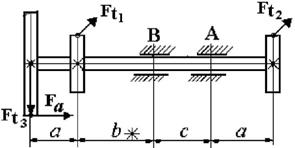
25 схема                                                              26 схема

5   6

 

 

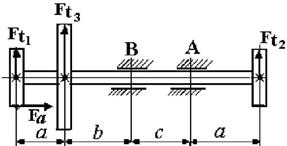
27 схема                                                               28 схема

7   8

 

 

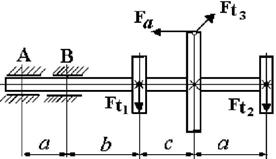
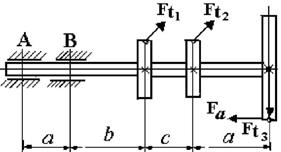
29 схема                                                           30 схема

9   10

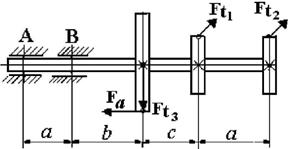
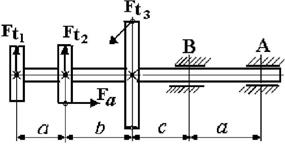
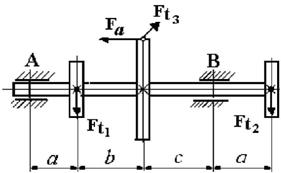
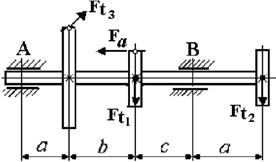
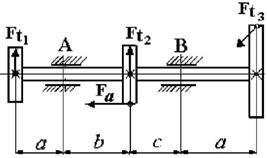
Рис. 4.2

 

 

Задача 5. Подбор  диаметра стального вала работающего на изгиб с кручением

Стальной вал постоянного сечения вращается с частотой n (об/мин) и передает мощность N (кВт).

Требуется подобрать диаметр ва­ла из условия его прочности при совместном действии изгиба и кручения, если изв­е­­стны предел текучести материала σT и коэффициент запаса прочности nт=3.

Числовые данные берутся из табл. 5.1, расчетные схемы на рис. 5.

Необходимые характеристики материала приведены в табл. 5.2.

Таблица 5.1

Номер

строки

Схема

по рис. 5

Размер, м

N,

кВт

n,

об/мин

Марка

стали

a

B

c

D1

D2

01

1

0,5

0,3

0,3

0,4

0,6

20

120

10

02

2

0,4

0,5

0,5

0,2

0,6

15

380

20

03

3

0,3

0,7

0,3

0,3

0,5

10

380

25

04

4

0,4

0,3

0,5

0,2

0,4

16

280

3

05

5

0,6

0,8

0,4

0,4

0,6

18

280

30

06

6

0,4

0,5

0,3

0,3

0,6

12

120

35

07

7

0,5

0,3

0,3

0,2

0,5

14

120

4

08

8

0,6

0,4

0,5

0,5

0,5

20

280

10

09

9

0,4

0,6

0,3

0,4

0,4

15

380

3

10

10

0,8

0,4

0,7

0,3

0,5

17

380

30

 

в

г

а

б

в

г

д

а

д

 

1 схема                                                               2 схема

1   2

 

 

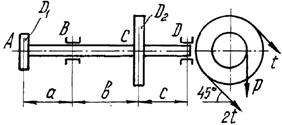
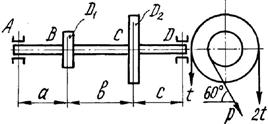
3 схема                                                              4 схема

3   4

 

 

5 схема                                                                      6 схема

5   6

 

 

7 схема                                                                    8 схема

7   8

 

 

9 схема                                                                   10 схема

9   10

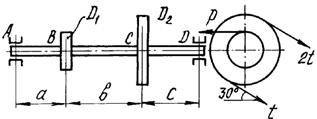
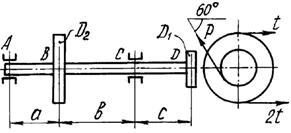
Рис. 5

 

Таблица 5.2

Марка

стали

Предел

текучести

σT, МПа

Предел

прочности

σв, МПа

Предел выносливости

при изгибе

σ-1, МПа

при кручении

τ-1, МПа

3

250

420

170 - 220

100 - 130

4

280

460

190 - 250

-

10

250

340

160 - 190

80 - 120

20

250

420

170 - 220

100 - 130

25

280

460

190 - 250

-

30

300

500

200 - 270

110 - 140

35

320

540

220 - 300

130 - 180

 

 

Задача 6. Подбор  диаметра стержня работающего на изгиб с кручением

Для прямого стержня, нагруженного по схеме, указанной на рис.6, необходимо:

1. Записать выражение для поперечной силы Qy(z), изгибающего Mx(z) и крутящего Mk(z) моментов.

2. Построить эпюры этих функций.

3. Выбрать опасное сечение.

4. Определить диаметр круглого поперечного сечения из расчета на прочность  по теории наибольших касательных напряжений.

5. Для выбранного стержня определить величину и направление главных напряжений в опасной точке.

Численные значения выбрать из таблицы под схемой нагружения по указанной строке варианта (таблица 6).

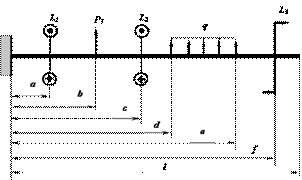
image177

Рис.6

 

Таблица 6

Номер

строки

l,

м

a,

м

b,

м

c,

м

d,

м

e,

м

f,

м

P1,

кН

q,

кН/м

L1,

кНм

L2,

кНм

L3,

кНм

[σ],

МПа

01

1,5

0,9

0,6

1,4

0

0,5

1

-0,8

-11

-0,5

-

-

108

02

1,7

1,3

0,5

0,6

0

0,5

1,5

0,9

12

-0,8

-

-

106

03

1,9

0,7

1,5

0,5

0,2

0,6

0,8

3,5

-13

0,9

-

1,5

102

04

1,4

1

0,6

0,5

0

0,8

0,9

-1,2

14

1

-

-

131

05

1,1

0,3

0,5

1

0,3

0,4

0,5

-2,5

-15

-1,2

-0,5

-

102

06

1,2

0,3

1

0,8

0,4

0,5

0,9

-3

16

-0,5

-0,8

-

124

07

1,7

1

0,7

1,7

0,4

0,5

0,3

2,9

-17

1,5

0,9

-

112

08

2,1

1

0,3

1,5

0,6

0,8

1,8

1

18

-

1

-

102

09

2,4

0,8

0,9

1,6

0,4

1

1,8

-1,2

-19

-

-1,2

-

102

10

2,4

0,7

0,4

1,7

0,6

1

1

-1,3

12

-

-0,5

-

142

11

1,7

0,8

0,5

0,9

0,3

0,8

1

1,5

-11

-

1,5

1,5

142

12

2,4

1,6

1

0,9

0,6

1,5

0,3

-1,8

12

1

0,5

-1,3

145

13

1,5

1

0,5

1,2

0,1

0,7

0,7

0,9

-13

1,5

0,8

-1,8

129

14

1,9

1,9

0,2

0,9

0,4

0,9

0,7

1

14

0,5

0,9

1,9

159

15

1,4

0,6

0,3

1,3

0,4

0,6

0,5

-1,2

-15

-0,8

-1

1,5

120

16

1,5

0,3

0,5

0,6

0,2

0,9

0,9

-2

16

-0,5

-

-

156

17

2,7

2

0,4

1

0,7

1,7

0,6

1,6

-17

-0,8

0,3

-

111

18

2,5

0,3

1

0,9

0,4

1,4

1,8

2,6

18

0,9

-

-

124

19

1,7

0,4

1

0,8

0,5

1,3

0,3

-2,3

-19

1

0,6

-

120

20

1,2

1

0,4

0,7

0,2

1

0,3

-1,5

10

-1,2

-0,5

-

113

21

1,9

0,4

0,6

1

0,3

1,5

1,9

-1,8

-11

-0,5

-0,8

-

172

22

2,3

0,5

1,3

1,6

0,5

2,3

0,6

1,9

12

1,5

0,9

-

100

23

1,7

1

0,7

0,8

0,3

1,6

1

3,6

-13

-

1

1,7

195

24

1

0,7

0,8

0,3

0,2

0,6

0,6

-3,5

14

-

-1,2

2,6

159

25

2,2

0,8

1,9

0,9

0,5

1,2

0,4

-1,5

-15

-

-0,5

1,5

194

26

2

1,3

0,8

0,6

0

1,5

0,3

2,6

16

-

1,5

-

108

27

2

2

0,9

1

0,1

1,6

0,3

-2,8

-17

1

0,5

-2,6

113

28

2,0

1

0,3

1,7

0,3

1,6

0,7

2,6

18

1,5

0,8

-3,2

135

29

1,3

0,7

0,8

0,4

0,3

0,9

0,7

2,6

-19

-0,5

-0,9

1,9

156

30

1,2

1

0,3

1,2

0,6

0,9

0,8

-3,8

10

-0,8

-1

2,5

194

 

а

г

в

г

д

а

д

в

а

б

а

в

б

 

 

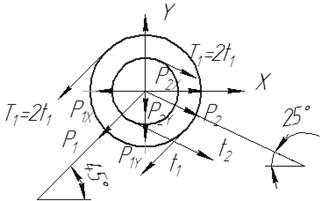
Задача 7. Расчет вала на изгиб с кручением

Вал с колёсами 1, 2, 3 вращается с частотой n оборотов в минуту и передаёт мощность N, кВт от колеса 1 поровну колесам 2 и 3 (рис.7).

Требуется:

1. Определить моменты и усилия, действующие на вал.

2. Построить эпюры крутящего момента Мк, изгибающих моментов Мх (от вертикальных сил), Му (от горизонтальных сил) и эпюру суммарного изгибающего момента Ми.

3. По наибольшему эквивалентному (расчетному) моменту Мэкв определить диаметр вала d при [𝜎]=70 МПа и округлить его до стандартного значения. Использовать гипотезу прочности наибольших касательных напряжений.

Числовые данные берутся из табл. 7, расчетные схемы на рис.7.

 

Мощность N = (50+α+3β) кВт,

Частота n = (600+10α+40β) об/мин,

Длина l = (0,5+0,05β) м,

Диаметр D1 = (0,6+0,05β) м,

Диаметр D2 = (0,5+0,05α) м,

Диаметр D3 = (0,5+0,05β) м,

Усилие T1=0,5P1, T2=0,5P2.

Таблица 7

Номер

строки

Схема

по рис.7

α

β

01

1

1,5

0,9

02

2

1,7

1,3

03

3

1,9

0,7

04

4

1,4

1

05

5

1,1

0,3

06

6

1,2

0,3

07

7

1,7

1

08

8

2,1

1

09

9

2,4

0,8

10

10

2,4

0,7

11

11

1,7

0,8

12

12

2,4

1,6

13

13

1,5

1

14

14

1,9

1,9

15

15

1,4

0,6

16

16

1,5

0,3

17

17

2,7

2

18

18

2,5

0,3

19

19

1,7

0,4

20

20

1,2

1

21

1

1,9

0,4

22

2

2,3

0,5

23

3

1,7

1

24

4

1

0,7

25

5

2,2

0,8

26

6

2

1,3

27

7

2

2

28

8

2,0

1

29

9

1,3

0,7

30

10

1,2

1

 

в

а

г

 

Рис.7

 

 

Примеры выполнения задач

 

Пример 1

Стальной вал постоянного сечения (рис.8, а) вращается с постоянной уг­ло­вой скоростью n = 120 об/мин и передает через шкив диаметром D2 = 0,6 м мощность N = 20 кВт.

Подобрать диаметр вала из условия его прочности, если вал изготовлен из стали марки Ст.50 с пределом текучести материала σт = 380 МПа  и коэф­фициент запаса прочности по отно­шению к пределу текучести nт= 3.

Остальные числовые данные к задаче: а = 0,3 м;  в = 0,3 м;  с = 0,2 м; D1 = 0,3 м.

Рис. 8. Расчетная схема и эпюры моментов внутренних усилий в поперечных сечениях вала

 

Решение.

1.Определение нагрузок, передающихся на вал.

На рис.8, а показаны усилия, приложенные к шкиву (сечение D) и к ше­стерне (сечение B).

Крутящий момент, передаваемый через шкив на вал:

Нагрузки, действующие на вал, определяются с учетом того, что окружные усилия, приложенные к шкивам, при переносе их в центр попе­речного сечения вала приводятся к силам, изгибающим его в двух плоскостях, и скру­чи­ва­ю­щему  моменту.

Шкив В

 

Шкив D

Расчетная схема вала показана на рис. рис.8,б.

 

2. Построение эпюр изгибающих и крутя­щего моментов.

Из условий нагружения вала следует, что он испытывает кручение на уча­стке BD постоянным крутящим моментом Mкр=1,62 кНм, эпюра ко­торого показана на рис.8,в.

Схема нагрузок, приложенных к валу в вертикальной плоскости, пред­став­лена  на рис.8,г. Для построения эпюры изгибающих моментов от дей­ствия этих сил, вал рассматривается как простая двухопорная балка, для которой следует вычислить­ вертикальные опорные ре­акции:

Σma=0;    10,83∙0,3 + 14,03∙0,8 - RCz∙0,6 =0;

RCz=24,12 кН;

Σmс=0;    RzA∙0,6 - 10,83∙0,3 + 14,03∙0,2 =0;

RzA =0,72 кН.

Проверка вычислений опорных реакций:

ΣY=0;   0,72 - 10,8 + 24,1 - 14,03 ≈ 0.

Вычисляем изгибающие моменты от действия вертикальных сил в харак­терных сечениях вала:

По вычисленным значениям построена эпюра изгибающих моментов My от действия сил, расположенных в вертикальной плоскости  (рис.8,д).

На рис.8,е показаны нагрузки, приложенные к валу в горизонтальной плоскости (для наглядности чертежа схема  повернута на 900).

Для построения эпюры изгибающих моментов от действия этих сил вычис­ля­ются горизонтальные опорные реакции:

Σma=0;    RyC∙0,6 – 8,1∙0,8 =0;

RyC=10,8 кН;

Σmс=0;    RyA∙0,6 + 8,1∙0,2 =0;

RyA = -2,7 кН.

Проверка  определения горизонтальных опорных реакций:

ΣY=0;   RyA + RyC – Qy = -2,7 + 10,8 - 8,1= 0.

Изгибающие моменты в характерных сечениях вала:

По вычисленным значениям момента строится эпюра Mz (рис.8,ж).

 

3. Подбор поперечного сечения (определение диаметра вала).

Материал вала - сталь марки Ст.50, допускаемое напряжение для кото­рой

Опасным для вала является сечение С, так как в этом сечении действует крутящий момент, а изгибающие моменты в вертикальной и горизон­таль­ной плоскостях максимальны (рис.8 в, д, ж).

Величины моментов в сечении С:

MyC = 2,806 кНм;   MzC = 1,62 кНм;    MкрC = 1,62 кНм.

Расчетный момент по третьей гипотезе прочности

Искомый диаметр вала:

 

 

Пример 2

Шкив с диаметром D1 и с углом наклона ветвей ремня к горизонту α1 вращается со скоростью n оборотов в минуту и передает мощность N кВт. Два других шкива имеют одинаковые диаметры D2 и одинаковые углы наклона ветвей ремня к горизонту α2, и каждый из них передает мощность N/2 (рис. 9).

Дано: N=60 кВт, n=500 об/мин,  D1=0,6 м,  D2=1,5 м,  a=1,3 м, b=0,6 м,  c=1,5 м,  =60°,  =50°.

Требуется:

1) определить моменты, приложенные к шкивам, по заданным величинам N и n;

2) построить эпюру крутящих моментов Mz;

3) определить окружные усилия t1 и t2, действующие на шкивы, по найденным крутящим моментами и заданным диаметрам шкивов D1 и D2;

4) определить давления на вал, принимая их равными трем окружным усилиям;

5) определить силы, изгибающие вал в горизонтальной и вертикальной плоскостях (вес шкивов и вала не учитывать);

6) построить эпюры изгибающих моментов от горизонтальных сил My и от вертикальных сил Mx;

7) вычислить значения суммарных изгибающих моментов, пользуясь формулой  и построить развертку эпюры суммарного изгибающего момента на плоскость, откладывая все ординаты в одну сторону от оси вала (при построении развертки эпюры надо учесть, что для некоторых участков вала она не будет прямолинейной);

8) при помощи эпюр Mz (см. п. 2) и Mи (см. п. 7) найти опасное сечение и определить величину максимального расчетного момента (по третьей теории прочности);

9) подобрать диаметр вала d при [σ]=70 МПа и округлить его величину.

Рис. 9

Решение.

Крутящие моменты в сечениях вала под шкивами:

Соответствующие этим крутящим моментам окружные усилия t1 и t2 определим из следующих формул:

аналогично имеем

Отсюда

Тогда приведенное к центру вала давление на вал в местах насадки шкивов будет равно

F1=3∙t1=3∙3,820=11,460 кН,

F2=3∙t2=3∙0,764=2,292 кН.

Горизонтальные и вертикальные составляющие давления на вал, вызывающие изгиб вала в соответствующих плоскостях, определяются следующим образом:

F1x=-F1cos60°=-11,460∙0,500=-5,730 кН,

F2x=F2cos50°=2,292∙0,643=1,473 кН,

F1y=-F1sin60°=-11,460∙0,866=-9,924 кН,

F2y=-F2sin50°=-2,292∙0,766=-1,756 кН.

Рис. 10

 

Расчетная схема представляет собой балку, установленную на двух шарнирных опорах и нагруженную сосредоточенными скручивающими моментами и сосредоточенными поперечными силами в вертикальной и горизонтальной плоскости (рис. 10).

Строим эпюры крутящих и изгибающих моментов. Для совмещения горизонтальной плоскости xoz (плоскость эп.My) с плоскостью страницы, повернем на 900 координатные оси yox относительно оси z.

Вычисляем значения суммарного изгибающего момента в характерных сечениях вала по формуле  .

Из эпюр Mкр и Mизг видно, что опасным является сечение 1, для которого =1,146 кНм и =10,09 кНм.

Для этого сечения вычисляем расчетный момент, используя третью теорию прочности. Получим

Из условия прочности вычисляем диаметр вала

Округлив значение диаметра, получим d =125 мм.

 

 

Пример 3

Вал круглого сечения (рис.11) вращается с частотой n=450 об/мин и передает мощность N1=40 кВт от колеса 1 поровну колесам 2 и 3.

Определить диаметр вала, используя гипотезу прочности наибольших касательных напряжений.

Дано: l=300 мм, D1=400 мм,  D2=300 мм,  D3=500 мм,  [σ]=80 МПа, T1=0,4P1,  T2=0,4P2.

Решение.

Находим моменты и усилия, действующие на вал.

Показываем вертикальные силы T2, P1, 3S, находим реакции Ay, By и строим эпюру изгибающего момента Mx.

Проверка

Показываем вертикальные силы P2, T1, находим реакции Ax, Bx и строим эпюру изгибающего момента My.

Рис.11

 

Проверка

Вычисляем суммарный изгибающий момент и строим эпюру Mи.

Строим эпюру крутящего момента Mк.

Вычисляем эквивалентный (расчетный) момент для опасного сечения А и из условия прочности находим диаметр вала:

Принимаем d=60 мм.

 

 

Пример 4

На вращающемся с частотой n сплошном валу (рис.12) установлены связанные с двигателями ременной передачей два ведущих шкива (I и II) с диаметрами D1 и D2, передающие валу мощности N1 и N2, а также ведомая шестерня с диаметром D3. Определить диаметр стального вала по III теории прочности, приняв допускаемое напряжение [σ] = 160 МПа.

Дано: N1 = 7 кВт;   N2 = 13 кВт;  n = 1000 об/мин;  D1 = 300 мм;  D2 = 150 мм;  D3 = 90 мм;  а1= 0 м;  а2 = 1,8 м;   а3= 1,0 м;   а4= 1,0 м;  а5=1,5 м;   α1 = 0°;  α2 = 270°;  α3 = 90°.

кручение.bmp

Рис.12

 

Решение.

1. Определение внешних моментов, действующих на вал.

От шкива I     

От шкива II   

ΣM = 0;    M1 + M2 – M3 = 0 ⇒   M3 = M1 + M2 = 0,067 + 0,125 = 0,192 кНм.

 

2. Определение крутящего момента Мкр.

Используем метод сечений по участкам.

Участок 1:   Мкр1 = 0.

Участок 2:   Мкр2 = М1 = 0,067 кНм.

Участок 3:   Мкр3 = М3 = 0.

 

3. Определение внешних изгибающих нагрузок

Приводим силы, приложенные к шкивам, к центру вала.

Силы, действующие по окружности шкивов

Приведенные силы

R1 = 3∙S1 = 3∙0,446 = 1,338 кН,

R2 = 3∙S2 = 3∙1,67 = 5,01 кН.

 

4. Построение эпюр изгибающих моментов

Вертикальная плоскость YOX

Определение опорных реакций.

ΣМВ = 0           YA∙1,8 - R2∙0,8 + P∙0,8 = 0

ΣМА = 0           YB∙1,8 – R2∙1 + P∙1 = 0

Определение изгибающих моментов.

Участок 1                  

Мz1 = YB∙x1

x1 = 0              Mz1 = 0;          

x1 = 0,8 м        Mz1 = 0,41∙0,8 = 0,33 кНм

Участок 2                  

Мz2 = YA∙x2

x2 = 0              Mz2 = 0;          

x2 = 1 м           Mz2 = 0,33∙1 = 0,33 кНм

 

Горизонтальная плоскость ZOX

Определение опорных реакций

ΣМВ = 0           ZA∙1,8 + R1∙0,3 = 0

ΣМА = 0           ZB∙1,8 + R1∙1,5 = 0

Определение изгибающих моментов

Участок 1                   Мy1 = ZB∙x1

x1 = 0              My1 = 0;          

x1 = 0,3 м        My1 = -1,115∙0,3 = -0,334 кНм.

Участок 2                  

Мy2 = ZA∙x2

x2 = 0              My2 = 0;          

x2 = 1,5 м        My2 = -0,223∙1,5 = -0,334 кНм.

Суммарный изгибающий момент определим по формуле

 

5. Определение диаметра вала

Опасные сечения I-I и II-II

Эквивалентный момент по III теории прочности

Опасное сечение II-II. Условие прочности

 

 

Пример 5

Вал круглого сечения (рис.13) вращается с частотой n=360 об/мин и передает мощность N=26 л.с.=19,1 кВт от колеса 1 поровну колесам 2 и 3.

Определить диаметр вала, используя третью теорию прочности.

Дано: а=1,2 м; b=0,6 м; с=1,1 м; D1=450 cм; D2=400 см; .

Задача4

 

Задача4

Рис.13

 

Решение.

1) Определение моментов, приложенных к шкивам.

Момент на шкивах по передаваемой мощности и скорости вращения вала определяется по формуле

где N - передаваемая валом мощность, Вт,

– угловая скорость вращения вала, рад/с.

Угловую скорость можно вычислить по формуле

Вычисляем момент на первом шкиве:

Моменты на втором и третьем шкивах будут одинаковыми и равны половине момента первого шкива

Построим эпюры крутящих моментов.

 

2) Определение окружных усилий.

Спроектируем усилия  и  на координатные оси x и y:

3) Определяем силы, изгибающие вал в горизонтальной и вертикальной плоскостях, и строим эпюры изгибающих моментов.

Рассматриваем изгиб вала в плоскости ZOX.

Проверка:  .

Рассматриваем изгиб вала в плоскости YOZ.

Проверка: 

 

4) Построим эпюру суммарных изгибающих моментов

Находим суммарный момент по формуле:

5)  Определение опасного сечения и величины максимального расчетного момента по третьей теории прочности.

Из эпюр MK и Mu видно, что опасное сечение будет в точке C, где:

MK=253,44 Нм;  Mu=157,7 Нм.

6) Условие прочности вала по третьей теории прочности определяется по формуле:

где  - осевой момент сопротивления сечения. Для круга:

Принимаем диаметр вала: d=40 мм.

 

 

Пример 6

Шкив (рис.14) с диаметром D1=1,1 м и углом наклона ветвей ремня к горизонту  делает n=500 оборотов в минуту и передает мощность N=120 кВт. Два других шкива имеют одинаковый диаметр D2=0,6 м и угла наклона ветвей ремня к горизонту  и каждый из них передает мощность N/2.

Требуется:

1) определить моменты приложенные к шкивам, по заданным N и n и построить эпюру крутящих моментов Mкр;

2) определить окружные усилия f1 и f2, действующие на шкивы, по найденным моментам и заданным диаметрам шкивов D1 и D2;

3) определить нагрузки, действующие на вал, принимая их равными трем окружным усилиям;

4) определить силы, изгибающие вал в вертикальной и горизонтальной плоскостях (массу шкивов и вала не учитывать);

5) построить эпюры изгибающих моментов от горизонтальных сил MГ и от вертикальных сил МВ;

6) построить эпюру суммарных изгибающих моментов МИ;

7) найти опасное сечение вала и определить расчетный момент, пользуясь третьей теорией прочности;

8) подобрать диаметр вала по заданному значению [ и округлить расчетное значение до ближайшего: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 и далее через 10 мм.

 

9-1a

Рис.14

Решение.

1) Определение моментов, приложенных к шкивам.

Момент на шкивах по передаваемой мощности и скорости вращения вала определяется по формуле

где N - передаваемая валом мощность, Вт,  – угловая скорость вращения вала, рад/с.

Угловую скорость можно вычислить по формуле

Вычисляем момент на первом шкиве:

Моменты на втором и третьем шкивах будут одинаковыми и равны половине момента первого шкива

М2=М3=М1/2=1145,9 Нм

Построим эпюры крутящих моментов. Так как подшипники вала крутящий момент не воспринимают, то на участках АВ и D К крутящий момент равен нулю. 

Участок АВ: Мk1=0.

Участок ВС:   

Участок СD:   

Участок DK:

По полученным значениям построим эпюpy Mk (рис.15)

Рис.15

 

2) Определение окружных усилий.

Моменты на шкивах можно записать как разность окружных усилий, умноженную на радиус шкива, т.е. М = ( Т - t )·D/2.

  откуда

  откуда

3) Рассчитываем усилия на вал от окружных усилий (рис.16).

Обозначим окружные усилия:

 

Рис.16

 

4) Спроектируем усилия P1 и P2 на координатные оси x и y:

и  действуют в горизонтальной плоскости и имеют противоположные направления.

и  действуют в вертикальной плоскости и имеют одинаковые направления.

5) Построение эпюр изгибающих моментов от горизонтальных и от вертикальных сил.

а) Изгиб вала от горизонтальных сил (подшипники вала принимаются за шарнирные опоры).

Определение опорных реакций.

Откуда:

Отрицательное значение  говорит, о том, что реакция опоры направлена в отрицательную сторону оси x.

Откуда:

Проверим правильность найденных реакций:

Для построения эпюры Mгор рассмотрим каждый участок вала в отдельности.

На участке AB ():        

Тогда  ;  .

На участке ВС ():     

Тогда

На участке KD ():  ;  

На участке DC ():  ; 

По вычисленным значениям строим эпюру (рис.17):

Рис.17

 

б) Изгиб вала от вертикальных сил.

Определяем опорные реакции:

Проверяем полученные результаты:

Следовательно, реакции опор определены правильно.

Построение эпюры .

На участке AB ():    

Тогда  ; 

На участке ВС ():     

Тогда  ; 

На участке KD ():  ;  

На участке DC ():  ;   

По вычисленным значениям строим эпюру (рис.18):

 

Рис.18

 

6) Построим эпюру суммарных изгибающих моментов

Находим суммарный момент по формуле:

на опорах

В точке В:

В точке С:

В точке D:

По вычисленным значениям строим эпюру (рис.19):

 

Рис.19

 

7) Определение опасного сечения и величины максимального расчетного момента по третьей теории прочности.

Из эпюр MK и Mu видно, что опасное сечение будет в точке С, где MK=2291,8 Нм; Mu=23832,8 Нм.

8) Условие прочности вала по третьей теории прочности определяется по формуле

где  - осевой момент сопротивления сечения. Для круга:

Тогда

Принимаем диаметр вала с запасом: d=140 мм.

 

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

 

Теоретическая механика   Сопротивление материалов

Строительная механика  Детали машин  Теория машин и механизмов

 

 

 

00:00:00

 

Top.Mail.Ru