Главная

Лекция 2 (продолжение). Примеры решения на осевое растяжение – сжатие

Расчет статически неопределимых стержневых систем на растяжение-сжатие. Расчеты по допускаемым напряжениям

Пример 1.

Составить полную систему уравнений и определить усилия в стержнях.

Р е ш е н и е.

1. Схема (рис. 1):

А₁ = А₂ = А₃ = А.

Уравнения статики

, , (1)

, . (2)

Рис.1

Уравнение совместности деформаций. Деформации стержней

, , .

Из подобия треугольников АВ₁В₂ и AD₁D₂ имеем

откуда, выражая удлинения через усилия по закону Гука

, , ,

получим 6N₂- 3N₁ = 2N₃.

Решая совместно уравнения (1), (2) и (3), найдем

N₁ = (2/35)F, N₂ = (9/35)F, N₃ = (24/35)F.

2. Схема (рис. 2):

Е₂ = 2Е₁ = 2Е,

А₁ = 2А₂ = 2А.

Уравнение статики. Из условия равновесия узла В имеем

, 2N₁cos30° + 2N₂cos60° = F. (4)

Уравнение совместности деформаций (рис. 2, в)

, откуда, выражая деформации через усилия ,

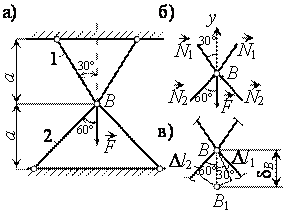
Рис.2

, получим N₁ = 3N₂. (5)

Решая совместно уравнения (4) и (5), найдем

N₁ = 0,27F; N₂ = 0,09F.

3. Схема (рис. 3).

Уравнения статики (рис.3, б).

У з е л А

, . (6)

У з е л В

, . (7)

Рис.3

Уравнение совместности деформаций

, , .

Выразив удлинения через усилия по закону Гука, получим

. (8)

Решая совместно уравнения (6), (7) и (8), найдем усилия в стержнях.

Пример 2.

Невесомая жесткая балка подвешена на трех одинаковых стержнях и нагружена силой F. Во сколько раз уменьшится напряжение в среднем стержне, если площадь его сечения увеличить в 4 раза.

Р е ш е н и е.

1. Определение усилий. Данная система является 1 раз статически неопределимой. Поэтому в дополнение к уравнению статики необходимо составить одно уравнение совместности деформаций.

Уравнение статики: , 2N₁+ N₂ = F. (1)

Уравнение совместности деформаций или, заменяя деформации через усилия по закону Гука,

N₁l/(EA₁) = N₂l/(EA₂), откуда

N₂ = (A₂/A₁)N₁ = mN₁, (2)

где m = A₂/A₁ отношение площадей.

Решая совместно (1) и (2), найдем

N₁ = F/(2 + m), N₂ = Fm/(2 + m).

2. Исследование напряжений при изменении жесткости конструкции. Находим напряжения в стержнях

Пусть в исходном состоянии А₁ = А₂ = А, т.е. m = 1. Тогда N₁ = N₂ = F/3 и .

После увеличения площади поперечного сечения среднего стержня в 4 раза (m = 4) будем иметь

N₁ = F/6, N₂ = 2F/3 и ,

т.е. напряжения в среднем стержне уменьшаются в 2 раза. Как видим, напряжения уменьшаются в меньшей пропорции, чем увеличивается площадь сечения. Это связано с тем, что одновременно с увеличением площади сечения стержня возрастает и усилие в нем. В статически определимых системах усилия не зависят от площади поперечных сечений стержней, поэтому увеличение площади сечений сопровождается пропорциональным уменьшением напряжений.

Пример 3.

Дана статически неопределимая плоская шарнирно - стержневая система, состоящая из абсолютно жесткого бруса, опертого на шарнирную опору и прикрепленного к двум стержням ВВ₁ и СС₁ при помощи шарниров.

Площади поперечных сечений показаны на рис. а.

Определить нормальные усилия в стержнях ВВ₁ и СС₁.

Решение.

На рис. б показана расчетная схема рассматриваемой шарнирной системы, где N₁, N₂ – нормальные силы, возникающие в стержнях ВВ₁ и СС₁; V, H – вертикальная и горизонтальная составляющая опорной реакции шарнирно-непод-вижной опоры О; F – внешняя сосредоточенная сила, приложенная к абсолютно жесткому брусу ВD. Таким образом, имеем четыре неизвестные реакции (N₁, N₂, V, H,) и три уравнения равновесия (,,). Следовательно, данная система является один раз статически неопределимой и для ее решения требуется составить одно дополнительное уравнение перемещений.

Запишем уравнение равновесия

(а)

которое содержит две неизвестные нормальные силы N₁и N₂. Для составления дополнительного уравнения перемещений рассмотрим деформацию системы, предположив, что абсолютно жесткий брус ВD при деформации повернется вокруг опоры О (рис. б, пунктирная линия В^/ОD^/), оставаясь прямым.

Из подобия треугольников ВВ^/О и DD^/О находим:

или (б)

Из-за малости перемещений будем полагать, что точки В, С, D при деформации системы переместятся соответственно в точки В^/, С^/, D^/, т.е. перемещения точек абсолютно жесткого бруса будут происходить вертикально. Определим удлинения стержней ВВ₁ и СС₁:

(в)

но с другой стороны при рассмотрении рис. б можно получить

и или

а с учетом формул (в) имеем (г)

Приравняем соответствующие части формул (б) и (г):

(д)

Таким образом, получена система двух уравнений (а) и (д) с двумя неизвестными N₁ и N₂, решая которую находим

Пример 4.

Пространственный кронштейн, состоящий из трех стержней, нагружен силой F. Зная допускаемые напряжения материала стержней на растяжение [] = 120 МПа и на сжатие [] = 60 МПа, требуется:

1) проверить прочность конструкции, если F = 120 кН, А₁ = А₂ = 4 см², А₃ = 25 см²;

2) подобрать сечения стержней из двух равнобоких уголков, если F = 480 кН;

3) определить, какой груз может выдержать кронштейн, если А₁ = А₂ = 10 см², А₃ = 60 см².

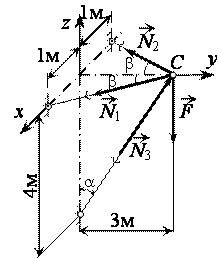
Решение.

1. Определение усилий в стержнях. Из условия равновесия узла С имеем:

, , ;

, , .

2. Определение искомых величин.

2.1. Проверка прочности конструкции

Находим напряжения в стержнях:

= 0,395×120×10³/(4×10^-4) = 118,5 МПа<[] = 120 МПа;

1,25×120×10³/(25×10^-4) = 60 МПа = [] = 60 МПа.

Как видим, оба условия прочности выполняются, т.е. прочность конструкции в целом обеспечена.

2.2. П о д б о р с е ч е н и й

Из условия прочности на растяжение

откуда .

Из условия прочности на сжатие

откуда .

Принимаем по ГОСТ 8509-72 (СТ СЭВ 104-74):

- для 1-го и 2-го стержней – 2 уголка 70х70х6 (А₀₁ = 2 × 8,15 =16,3 см²);

- для 3-го стержня – 2 уголка160х160х16 (А₀₃ = 2 × 49,1 =98,2 см²).

2.3. Определение допускаемой нагрузки

Из условия прочности на растяжение

откуда .

Из условия прочности на сжатие

откуда .

Допускаемая нагрузка равна меньшей из найденных величин, т.е.

F = min{[F_р], [F_сж]} = [F_сж] = 288 кН.

Расчет статически неопределимых стержневых систем на растяжение-сжатие. Расчеты по предельным нагрузкам

Метод расчета по предельным нагрузкам исходит из более широкого использования экспериментальных данных, анализа пластических свойств материалов и их учета.

В этом методе путем расчета определяются не напряжения, а находится предельная нагрузка F_пред, при которой конструкция становится непригодной для эксплуатации. За допускаемую нагрузку принимается доля от предельной [F_F] = F_пред/П и условие прочности в данном случае принимает вид

При определении предельной нагрузки действительную диаграмму растяжения материала заменяют идеализированной диаграммой Прандтля, в которой площадка текучести принимается неограниченной (см. рис.). Поэтому расчет по допускаемым нагрузкам применим лишь для конструкций, выполненных из пластичных материалов и только при действии статических нагрузок.

Теоретическое определение допускаемой нагрузки возможно только для некоторых простейших случаев. Один из подходов состоит в том, что рассматриваются различные кинематически возможные схемы исчерпания несущей способности системы (система становится геометрически изменяемой). Продольные усилия в элементах, появление текучести в которых приводит к исчерпанию несущей способности конструкции, принимаются равными произведениям допускаемых напряжений на площади поперечных сечений. Из уравнений предельного равновесия определяются допускаемые нагрузки, соответствующие каждому из вариантов исчерпания несущей способности. В качестве допускаемой нагрузки для конструкции принимается наименьшая из найденных величин.

Пример 5.

Определить величину допускаемой нагрузки для данной конструкции, если А₁=А₂=А₃=А, l₁=l₂=l₃=l. Все стержни изготовлены из одного и того же материала.

Р е ш е н и е.

Данная система является один раз статически неопределимой (три неизвестных при двух независимых уравнениях статики). Несущая способность ее будет исчерпана (система станет геометрически изменяемой), когда возникнут пластические деформации в двух стержнях. Таких вариантов три.

Первый вариант (рис. б). Несущая способность исчерпывается при появлении пластических деформаций в 1-м и 2-м стержнях. Принимаем N₁ = N₂ = []A и составляем уравнение моментов относительно точки С: ,

, откуда .

В т о р о й в а р и а н т (рис. в). Несущая способность исчерпывается при появлении пластических деформаций в 1-м и 3-м стержнях. Принимаем N₁ = N₃ = []A и составляем уравнение моментов относительно точки В: ,

, откуда .

Т р е т и й в а р и а н т (рис. г). Несущая способность исчерпывается при появлении пластических деформаций во 2-м и 3-м стержнях. Принимаем N₁ = N₂ = []A и составляем уравнение моментов относительно точки А: ,

, откуда .

Допускаемой нагрузкой для конструкции будет наименьшая из трех найденных величин:

Пример 6.

Подобрать сечения стержней, если А₁=А₂=А₃=А, F=870 кН, допускаемое напряжение []= 150 МПа.

Решение.

1.Определение допускаемой нагрузки. Несущая способность конструкции будет исчерпана, когда пластические деформации возникнут во всех трех стержнях. Полагая N₁ = N₂ = N₃ = []А и составляя уравнение моментов относительно точки О, найдем допускаемую нагрузку

, ,

откуда .

2. Подбор сечений. Записываем условие прочности

откуда находим искомую площадь

Пример 7.

Для абсолютно жесткого бруса, опирающегося на шарнирно неподвижную опору и прикрепленного к двум стержням (рисунок 1), требуется:

1. Найти усилия и напряжения в стержнях, выразив их через силу Q.

2. Найти допускаемую нагрузку , если = 160 МПа =1600 кг/см², l₁=l₂=l=2 м, a = b = c = 2 м, A₁=A₂= 10 см², = 45º.

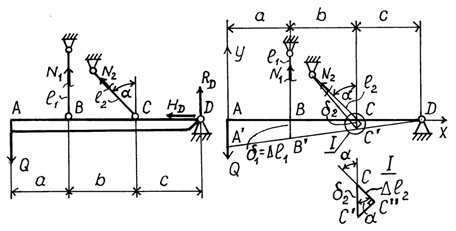
а) б)

Решение.

1. Найдем усилия в стержнях, выразив их через неизвестную силу Q.

Составим уравнения статического равновесия (рис. а):

; ; (1)

; ; (2)

; . (3)

Задача один раз статически неопределима, т.к. имеет четыре неизвестных (N₁, N₂, R_D, H_D) и три уравнения статического равновесия. Составим дополнительное уравнение.

Условие совместности перемещений получим, представив систему в деформированном состоянии – положение (рис. б). Из подобия треугольников и следует:

, (4)

но , а из треугольника

Подставив и в (4), получим:

или (5)

Из закона Гука

Тогда (5) примет вид: .

Подставив исходные данные, получим:

. (6)

Решая совместно (3) и (6), вычисляем N₂:

; ;

из (3): ; .

Определим напряжения в стержнях:

; . (7)

2. Определим допускаемую нагрузку . Так как в нашем случае , то, приравняв , получим с учетом (7):

(8)

Пример 8.

Для статически неопределимой системы, изображенной на рис. а (см²; см²; м; м; м; м, м), требуется определить усилия и напряжения в стальном ( кН/см²; кН/см²) и в медном ( кН/см²; кН/см²) стержнях, выразив их через силу P, а также найти допускаемую нагрузку .

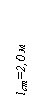
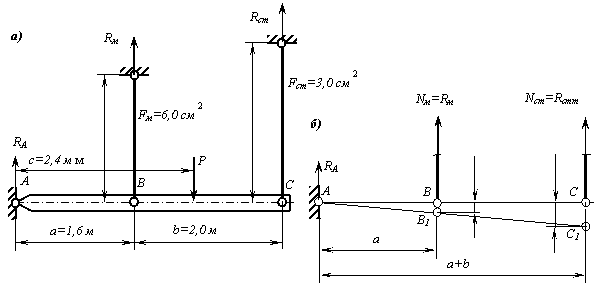
Решение.

1. Находим усилия и напряжения, возникающие в стержнях.

Рассечем стержни и изобразим систему в деформированном состоянии (рис. б). Под действием силы P абсолютно жесткий на изгиб брус повернется на некоторый малый угол, оставаясь прямолинейным. Поскольку угол поворота абсолютно жесткого на изгиб бруса мал, можно предположить, что его точки В и С будут перемещаться не по дуге окружности, а по вертикали вниз. Деформированное положение системы показано на рис. б наклонной прямой линией АС₁. Очевидно, что оба стержня, поддерживающие брус, растянутся. Поэтому внутренние усилия и , возникающие в поперечных сечениях этих стержней, направим от сечения. Удлинение медного стержня равно отрезку , а стального – отрезку .

Для плоской системы параллельных сил мы имеем два независимых уравнения статики. Неизвестных же у нас три: , и . Следовательно, заданная система является один раз статически неопределимой.

Чтобы исключить из дальнейшего рассмотрения реакцию , возникающую в шарнире A, составим следующее уравнение равновесия:

. (1)

В него входят две неизвестные и , поэтому для их определения (то есть для раскрытия статической неопределимости) нам необходимо составить еще одно, дополнительное, уравнение.

Очевидно, что удлинения стержней и связаны между собой. Из подобия треугольников ABB₁ и AСС₁ следует, что

Или, учитывая закон Гука,

. (2)

Полученное нами дополнительное уравнение (2), связывающее деформации стержней, называется уравнением совместности деформаций.

Подставив в (1) и (2) исходные данные задачи и выполнив несложные преобразования, получим следующую систему уравнений относительно неизвестных внутренних усилий и :

Отсюда находим, что усилия в стержнях равны:

Тогда напряжения

2. Определяем допускаемую нагрузку .

Из условия прочности медного стержня

кН/см²

находим, что

кН.

Из условия прочности стального стержня

кН/см²

следует, что

кН.

Принимая меньшее из найденных выше двух значений, находим, что допускаемая нагрузка для заданной системы равна кН.

Пример 9.

Для трехстержневой системы (рис.1, а) требуется: раскрыть статическую неопределимость; определить допускаемое значение силы Р; определить нагрузку предельного упругого состояния и нагрузку, соответствую исчерпанию несущей способности (нагрузку предельного пластического состояния) и резерв прочности.

Рис. 1

Решение.

1. Раскроем статическую неопределимость системы

Вырежем узел А, действие отброшенной части заменим усилиями (рис. 1, б), при этом будем полагать, что они растягивающие. В результате получили систему сходящихся сил, для которой можно составить 2 уравнения равновесия. Число неизвестных усилий равно трем, следовательно, данная система один раз статически неопределимая (или на систему наложена одна лишняя связь).

Составим уравнения равновесия

Из первого уравнения получим

тогда второе уравнение равновесия примет вид

Для раскрытия статической неопределимости составим дополнительное уравнение совместности перемещений, рассмотрев систему в деформированном состоянии (рис. 2).

Рис.2

Для определения удлинения наклонного стержня 1 нужно из деформированного состояния (т.A₁) восстановить перпендикуляр на первоначальное положение стержня. В результате получим т.A₂, а отрезок AA₂ будет удлинением рассматриваемого стержня.

Из получим

или .

Выразим деформации стержней через усилия

Соотношение (2) примет вид

где , – длины стержней.

Тогда:

Перемещение точки A будет равно

Напряжения в стержнях

2. Определим допускаемое значение силы из расчета по допускаемым напряжениям

Примем l=1,5 м; F=4 см²=4м²; МПа;

Условие прочности имеет вид

Из предыдущего расчета имеем

откуда

Примем кН тогда усилия в стержнях

кН

кН.

Перемещение точки А

Напряжения в стержнях

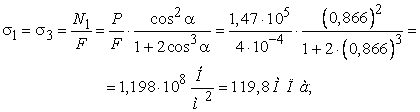
3. Определим нагрузку предельного упругого состояния

Эта нагрузка соответствует состоянию системы, когда в ней впервые возникнут пластические деформации, т.е. .

Примем предел текучести материала стержней МПа, тогда коэффициент запаса

Таким образом,

откуда

Необходимо отметить, что в рассматриваемом случае напряжения , т.е. они остаются в упругом состоянии.

Допускаемое значение силы

кН.

4. Определим нагрузку предельного пластического состояния, т.е. нагрузку, соответствующую исчерпанию несущей способности

В рассматриваемой системе исчерпание несущей способности произойдет, когда во всех стержнях напряжения достигнут предела текучести, т.е.

Подставим значения усилий в уравнение (1):

откуда

Если использовать для силы тот же коэффициент запаса , получим допускаемое значение силы

кН.

Резерв прочности

или 18,8%.

Величина показывает, какой резерв прочности таит в себе расчет по предельным нагрузкам по сравнению с расчетом по допускаемым напряжениям.

Пример 10.

Абсолютно жесткий брус (см. рис.) опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров.

Дано: А=14 см² , l₁=3,8 м; l₂=2,6 м; l₃=1,6 м; =120 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

3. предельную грузоподъемность системы, считая, что в обоих стержнях напряжения достигли предела текучести —

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместимости деформаций

По закону Гука

Подставляя в уравнение совместности деформаций, получим

Подставляя в уравнение статики, получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 1

Находим предельную грузоподъемность системы, считая, что в обоих стержнях напряжения достигли предела текучести — :

Тогда из уравнения статики

Пример 11.

Дано: А=16 см² , l₁=2,5 м; l₂=2,1 м; l₃=1,6 м; =120 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

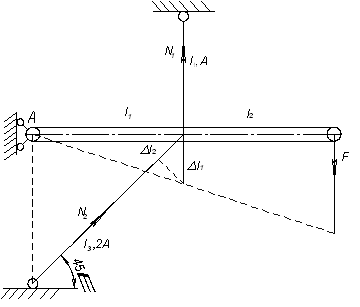
Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместности деформаций

По закону Гука

Подставляя в уравнение совместности деформаций, получим

Подставляя в уравнение статики, получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 1

Тогда из уравнения статики

Пример 12.

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров.

Дано: А=14 см² , l₁=2,3 м; l₂=2,8 м; l₃=1,8 м; =120 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

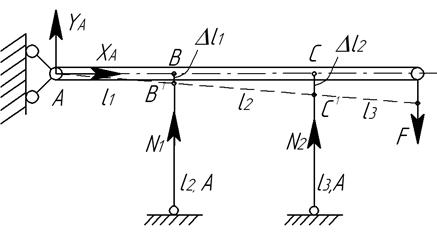
Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместности деформаций

По закону Гука

Подставляя в уравнение совместности деформаций, получим

Подставляя в уравнение статики, получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 2

Тогда из уравнения статики

Пример 13.

Дано: А=11см², l₁=2,2м; l₂=2,6м; l₃=1,2м; =140 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместимости деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 2

Тогда из уравнения статики

Пример 14.

Дано: А=20 см² , l₁=2,6м; l₂=2,6м; l₃=1,6м; =120МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

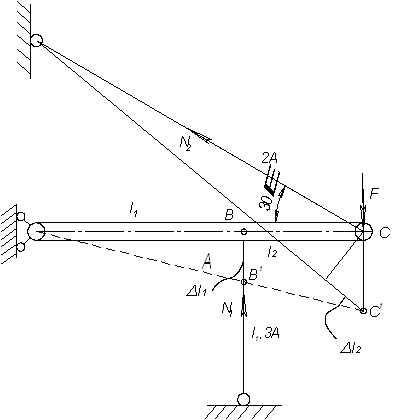
Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместности деформаций

По закону Гука

Подставляя в уравнение совместности деформаций, получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 2

Тогда из уравнения статики

Пример 15.

Дано: А=24 см² , l₁=3,0 м; l₂=2,6 м; l₃=1 м; =120 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместности деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 2

Тогда из уравнения статики

Пример 16.

Дано: А=12 см² , l₁=2,4 м; l₂=2,8 м; l₃= l₁+ l₂=5,2 м; =100 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместимости деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 1

Тогда из уравнения статики

Пример 17.

Дано: А=14 см² , l₁=3,4 м; l₂=2,8м; l₃=1,8м; =120 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместности деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 1

Тогда из уравнения статики

Пример 18.

Дано: А=10 см², l₁=2,1м; l₂=2,4 м; l₃=1,2 м; =100 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместимости деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 1

Тогда из уравнения статики

Пример 19.

Дано: А=10 см² , l₁=2,1 м; l₂=2,4 м; l₃=1,2 м; =100 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместности деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 1

Тогда из уравнения

Пример 20.

Дано: А=10 см² , l₁=2,1 м; l₂=2,4 м; l₃=1,2 м; =100 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместности деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 2

Тогда из уравнения статики

Пример 21.

Дано: А=10 см² , l₁=2,1 м; l₂=2,4 м; l₃=1,2 м; =100 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместности деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 1

Тогда из уравнения статики

Пример 22.

Дано: А=10 см² , l₁=2,1м; l₂=2,4 м; l₃=1,2 м; =100 МПа; К=2

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу F;

2. допускаемую нагрузку , приняв большее из напряжений в двух стержнях допускаемому напряжению МПа;

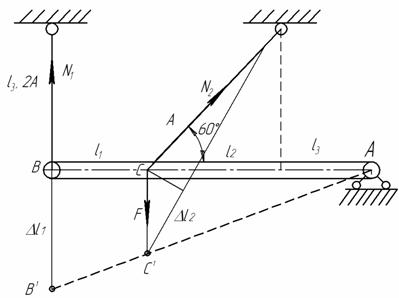
Решение.

Составляем уравнение статики

Дополнительное уравнение из условия совместимости деформаций

По закону Гука

Подставляя в уравнение совместности деформаций получим

Подставляя в уравнение статики, получим

Напряжения в стержнях

Сравнивая стержни 1 и 2 видим, что опасным является стержень 1

Тогда из уравнения статики

Пример 23.

Стержневая конструкция, состоящая из абсолютно жесткого диска и двух деформируемых стержней длиной l₁ и l₂, соединенных шарнирами, подвержена действию силы F (рис. 1).

Рис.1

Расчет этой конструкции состоит из трех частей:

Часть 1. Расчет по упругой стадии деформации. В зависимости от исходных данных, надо либо определить грузоподъемность конструкции, либо подобрать размеры поперечного сечения расчетом по допускаемым напряжениям.

Часть 2. Расчет по предельному пластическому состоянию. Требуется найти грузоподъемность (или подобрать сечения стержней) расчетом по предельному состоянию.

Часть 3. Определение дополнительных напряжений, связанных с изменением температуры на или неточностью изготовления одного из стержней. Допустим, что в рассматриваемой задаче стержень 1 охлаждается (), и найдем возникающие в стержнях конструкции температурные напряжения.

Решение.

Прежде всего убедимся, что рассматриваемая конструкция является статически неопределимой. Сосчитаем число неизвестных: ими являются продольные силы в двух деформируемых стержнях и две опорные реакции в шарнирно неподвижной опоре в точке А. Таким образом, имеем 4 неизвестные, а число независимых уравнений статики для данной системы равно 3. Система является один раз статически неопределимой.

Часть 1. Для расчета конструкции по упругой стадии деформации необходимо составить три группы уравнений:

- уравнения равновесия;

- уравнения совместности деформаций;

- физические уравнения (закон Гука).

Чтобы составить уравнения равновесия, нарисуем план сил. Для этого рассечем стержни и, отбросив части стержней, заменим их внутренними усилиями – продольными силами N₁ и N₂ (рис. 2, а). Важно, чтобы на плане сил направления усилий соответствовали плану перемещений. Для того, чтобы выяснить как направлены продольные силы в стержнях, нарисуем приближенный план перемещений (рис. 2, б). Точки В и С жесткого диска поворачиваются с радиусами AB и АС вокруг неподвижной точки А на один и тот же угол и перемещаются по дугам, которые заменяем перпендикулярами и Для того, чтобы найти абсолютные деформации стержней, надо из точек и (новые положения узлов В и С) опустить перпендикуляры на направления стержней. Как видно из рис. 2, б стержень 1 укорачивается на (выделенный жирным отрезок), и поэтому на плане сил усилие N₁ показано сжимающим. Стержень 2 согласно плану перемещений удлиняется на , и на рис. 2, а продольная сила N₂ нарисована растягивающей.

Рис.2

Теперь составим три уравнения равновесия:

; ;

; .

Запишем вторую группу уравнений – уравнения совместности деформаций. Поскольку данная система является один раз статически неопределимой, необходимо составить одно уравнение совместности деформаций. Это геометрическое уравнение, связывающее абсолютные деформации стержней, и его мы получим на основании плана перемещений. Из подобия треугольников ABB¢ и ACC¢ на рис. 2, б. Связывая отрезки BB¢ и CC¢ с деформациями стержней и и учитывая, что AB = a, а , получим окончательно уравнение совместности деформаций

Теперь надо связать деформации стержней с внутренними усилиями. Предполагая, что материал подчиняется закону Гука (расчет по упругой стадии деформаций), запишем третью группу уравнений

и .

Мы получили полную систему уравнений для определения всех неизвестных (). Как правило, нас интересуют только продольные силы в стержнях, поэтому из уравнений равновесия при решении системы используется только последнее уравнение, в которое не входят опорные реакции. Решая полученную систему уравнений, найдем внутренние усилия в стержнях:

;

Здесь введено обозначение – погонная жесткость i-го стержня.

Заметим, что, как видно из полученных формул, усилия зависят не только от величины нагрузки и геометрических размеров конструкции, как в статически определимых системах, но и от отношения погонных жесткостей стержней. Эта важная закономерность справедлива для любой статически неопределимой конструкции и позволяет влиять на распределение усилий в стержнях без изменения ее геометрической схемы.

Определив внутренние усилия в стержнях, находим напряжения и выбираем наиболее напряженный стержень. Из условия прочности этого (наиболее напряженного) стержня либо определяем допускаемую нагрузку, либо подбираем размеры поперечных сечений стержней (заданное отношение площадей сечения необходимо сохранить). Например, если в заданной схеме задаться следующими данными: м, м, , , м, м, то и , а .

Напряжения в стержнях , . Из сравнения видно, что наиболее напряженным является стержень 2. Из условия прочности этого стержня

находим либо значение F, либо А₁ (А₂ по заданному отношению равно А₁/2).

Для проверки рекомендуем после определения допускаемой нагрузки (либо размеров площадей сечения) еще раз найти напряжения в стержнях и убедиться в том, что условие прочности выполняется в обоих стержнях.

Часть 2. Сделаем расчет конструкции по предельному пластическому состоянию. Поскольку заданная система является один раз статически неопределимой, то в предельном состоянии должны потечь два стержня, то есть все деформируемые стержни конструкции. Для определения предельной нагрузки нарисуем план сил в предельном состоянии (рис. 3).

Рис.3

Направления усилий снова должны соответствовать плану перемещений. Составим одно уравнение равновесия в предельном состоянии (такое уравнение, в которое не входят неизвестные опорные реакции):

; .

Из этого уравнения можно найти значение предельной нагрузки. Для конкретных исходных данных, использованных в первой части задачи, получим:

Из условия прочности конструкции по предельному состоянию либо находим значение допускаемой нагрузки, либо подбираем размер А₁_.

Сравним величины допускаемых нагрузок, найденных разными методами для рассмотренного примера. Допускаемая нагрузка, определенная расчетом по упругой стадии деформации

оказалась меньше допускаемой нагрузки, полученной расчетом по предельному пластическому состоянию , на 56%.

Часть 3. Найдем дополнительные напряжения в стержнях конструкции, связанные с охлаждением стержня 1 на градусов. Предполагая, что в процессе деформации материал стержней остается упругим, расчет ведем по той же схеме, что и в первой части задачи, т. е. составляем три группы уравнений:

- уравнения равновесия;

- уравнения совместности деформаций;

- физические уравнения.

Рис.4

Уравнения равновесия составляем по плану сил (рис. 4, а), уравнения совместности деформаций – по плану перемещений (рис.4, б). План сил и план перемещений, как и раньше, должны соответствовать друг другу. Поясним особенности построения плана перемещений от температурного воздействия. Если бы конструкция была статически определимой, т. е. стержень 2 отсутствовал, то стержень 1 при охлаждении уменьшил бы свою длину на величину , жесткий диск повернулся бы на угол и узел В переместился в положение В¢¢. Поскольку конструкция статически неопределима, то лишний стержень 2 препятствует такой деформации. В результате жесткий диск повернется только на угол , точка В перейдет в положение В¢. Стержень 1 окажется растянутым на величину (выделенный жирным отрезок на плане перемещений рис. 4, б) и в нем возникнет растягивающее усилие N₁. В свою очередь стержень 2 в процессе деформации также будет растянут на величину продольной силой N₂. В соответствии с планом перемещений на плане сил (см. рис. 4, а) оба стержня показаны растянутыми.

Теперь запишем систему уравнений для определения внутренних усилий в заданной конструкции:

уравнение равновесия

; ;

уравнение совместности деформации (очевидно, что связь между деформациями стержней будет такой же, как и в первой части задачи, поэтому уравнение совместности деформаций в третьей части задачи можно записать, используя ранее полученное уравнение, заменив в нем на ).

и физические уравнения

; ; .

Решая эту систему уравнений, найдем усилия в стержнях системы, а далее по формуле температурные напряжения. Заметим, что отрицательный знак используется только при построении плана перемещений (стержень укорачивается от действия температуры), при решении системы уравнений величину следует принять положительной.

Примечание. Определение монтажных напряжений, связанных с неточностью изготовления одного из стержней , производится так же, как температурных напряжений. Например, если в рассмотренном примере стержень 1 будет изготовлен короче, чем требуется, на величину , то при сборке конструкции стержень 1 надо будет растянуть и при этом стержень 2 тоже растянется. На плане перемещений отрезок заменим на и решение задачи будет справедливо, если в полученной системе уравнений всюду заменить на заданную величину (отрицательный знак при решении системы уравнений не учитывается.)

Пример 24.

Имеется шарнирно-стержневая система, состоящая из трех деформируемых стержней, загруженная силой (рис. 1).

Заданы: геометрические характеристики системы (, , ); площади поперечных сечений стержней , , ; материал конструкции - пластичный.

Рис.1

Требуется:

1) определить грузоподъемность системы тремя способами:

- расчетом по упругой стадии деформаций;

- расчетом по упругопластической стадии;

- расчетом по предельному пластическому состоянию;

2) определить остаточные напряжения в стержнях системы при полной разгрузке из положения предельного равновесия.

Решение.

I. Определение грузоподъемности системы расчетом по упругой стадии деформаций

Найдем степень статической неопределимости системы. В данной конструкции имеем три неизвестные продольные силы в стержнях. Число уравнений статики, которые можно составить для системы сил, сходящихся в одной точке, равно двум. Таким образом, число неизвестных больше числа уравнений равновесия на единицу, и система является один раз статически неопределимой. Можно определить степень статической неопределимости и по-другому. Шарнир (модель которого - точка) для неподвижного закрепления на плоскости требует наложения двух линейных связей. Такими необходимыми связями являются любые два стержня из имеющихся трех стержней системы. Следовательно, оставшийся третий стержень становится лишней кинематической связью (лишним стержнем), а система является один раз статически неопределимой.

Для раскрытия статической неопределимости требуется составить уравнения статики, одно (по числу лишних связей) кинематическое соотношение (условие совместности деформаций) и физические уравнения. Рекомендуем начинать решение задачи с записи условия совместности деформаций, построив предполагаемый план перемещений. Для составления уравнений равновесия строим план сил, направления усилий на котором должны быть согласованы с планом перемещений.

1. Уравнение совместности деформаций. Построим предполагаемый план перемещений (рис. 2).

Рис.2

Величины двух абсолютных деформаций задаем произвольно (например, считаем, что стержни 2 и 3 удлиняются, и откладываем произвольные отрезки и вдоль стержней). На пересечении траекторий поворота концов двух стержней (перпендикуляров к направлениям стержней) получаем новое положение шарнира – точку С¢ на рис. 2. Опустив из этой точки перпендикуляр на направление оси стержня 1, найдем величину его абсолютной деформации .

Разложим полное перемещение шарнира – отрезок – на составляющие и . Найдем абсолютные деформации стержней, выразив их через и , используя их геометрическую связь:

Исключив из этих выражений и , получим искомое соотношение между абсолютными деформациями

Допускается составлять уравнение совместности деформаций приближенно, измеряя отношения между абсолютными деформациями по построенному в масштабе плану перемещений. Для приближенного определения связи между абсолютными деформациями представим эту связь в виде

Неизвестные параметры данной зависимости и определим из двух планов перемещений. При построении первого плана перемещений предположим, что . Измерим деформации первого и третьего стержней. Тогда

Построив второй план перемещений в предположении, что , найдем отношение деформаций первого и второго стержней и получим

2. Уравнения равновесия. Составим их на основании плана сил. Нарисуем план сил, вырезав узел и заменив отброшенные части стержней внутренними усилиями, причем направления усилий покажем в соответствии с планом перемещений растягивающими (рис.3).

Рис.3

Запишем два независимых уравнения статики. Для данной системы таковыми являются:

; ;

; .

3. Физические соотношения. Поскольку расчет ведется по упругой стадии деформаций, то материал конструкции подчиняется закону Гука и для каждого стержня записываем физические уравнения:

; ; .

Полученную систему уравнений решаем относительно усилий , , . Например, при , это решение имеет вид

, , .

Найденное решение показывает, что усилие в первом стержне отрицательно, т.е. стержень не растянут, как мы предполагали, а сжат. Полученные положительные знаки и подтверждают предположение о том, что эти стержни растянуты.

Для проверки прочности конструкции определим напряжения в стержнях системы:

;

При расчете по упругой стадии деформации считаем, что предельное состояние конструкции наступит тогда, когда потечет один, наиболее напряженный, стержень. Поскольку пластичный материал имеет одинаковые пределы текучести при сжатии и растяжении, то знак напряжения не имеет значения и первым потечет стержень, в сечении которого возникают наибольшие по модулю напряжения. В данном случае это третий стержень. Из условия его текучести находим предельную нагрузку:

, ;

а из условия прочности - допускаемую нагрузку на конструкцию:

, .

Отметим, что при расчете по упругой стадии деформаций нагрузка и напряжения на всем участке деформирования связаны прямой пропорциональной зависимостью, а потому коэффициенты запаса по напряжениям и по нагрузке равны между собой.

II. Определение предельной грузоподъемности системы расчетом по упругопластической стадии

Проследим за дальнейшим развитием процесса нагружения – деформирования системы после того, как напряжения в третьем стержне достигли предела текучести. Примем, что материал конструкции работает в соответствии с идеализированной диаграммой упругопластического тела – диаграммой Прандтля (рис. 4).

Рис.4

При продолжении роста нагрузки напряжения в третьем стержне будут оставаться постоянными и равными . При работе конструкции в упругопластической стадии напряжения в остальных стержнях будут расти в соответствии с упругим законом, но при изменившихся параметрах линейной зависимости от нагрузки. Эти изменения связаны с перераспределением нагрузки только на упругие стержни, обеспечивающие неизменяемость системы в этой стадии ее работы.

Поскольку усилие в стержне 3 уже известно, задача становится статически определимой и усилия в стержнях 1 и 2 находим из уравнений равновесия узла (план сил на рис. 5):

; ;

; .

Рис.5

Решение этой системы уравнений при , :

, .

Зависимости напряжений от нагрузки на данной стадии работы системы:

, .

Предельное пластическое состояние конструкции достигается тогда, когда напряжения в одном из упругих стержней 1 и 2 достигнут предела текучести и конструкция превратится в механизм. Определим, какой из стержней потечет первым, приравняв напряжения в стержнях пределу текучести и найдя, при каком значении нагрузки стержни потекут:

, ;

, .

Видно, что нагрузка, при которой , меньше и первый стержень потечет раньше второго. Нагрузка, при которой будут течь два стержня (3 и 1), и есть предельная нагрузка для всей конструкции

Заметим, что в предельном состоянии напряжения в первом и третьем стержнях достигли предела текучести. При этом первый стержень потек вслед за третьим, хотя к концу упругой стадии напряжения в нем были меньше, чем во втором стержне. Зависимость между напряжениями и нагрузкой с начала деформирования в упругопластической стадии уже не является линейной, а потому одинаковым коэффициентам запаса по нагрузке и по напряжениям в наиболее напряженном упругом стержне будут соответствовать различные значения допускаемой нагрузки. Так, в нашем случае допускаемая нагрузка с коэффициентом запаса по напряжениям определяется из условия

; ; .

Если же исходить из коэффициента запаса по нагрузке, то

; ; .

Очевидно, что расчет по допускаемой нагрузке приводит к повышенному запасу прочности в отдельных стержнях системы, а расчет по допускаемым напряжениям не обеспечивает заданного коэффициента запаса по нагрузке. Поэтому значение допускаемой нагрузки принимаем из условия прочности по нагрузке: .

Следует отметить, что современными строительными нормами проектирования предусматривается раздельное применение коэффициентов надежности по нагрузке и по материалу. Условие прочности в этом случае приняло бы вид

где и - коэффициенты надежности (запаса) по нагрузке и по материалу соответственно.

III. Определение предельной грузоподъемности системы расчетом по предельному пластическому состоянию

Заданная система имеет три деформируемых стержня, один из которых является лишним, так как система один раз статически неопределима. В предельном состоянии, когда конструкция превращается в механизм, должны потечь два стержня (один лишний и один необходимый). В рассмотренных ранее способах решения этой задачи рассматривался порядок перехода материала стержней в пластическую стадию работы, было выяснено, какой стержень потечет первым, какой – вторым. При этом конструкция сначала работает в упругой стадии (материал всех стержней подчиняется закону Гука), затем переходит в упругопластическую стадию работы. Решение вопроса о предельной нагрузке на конструкцию, при которой последняя переходит в механизм, может быть получено и без рассмотрения упругой и упругопластической стадий работы конструкции. Для этого достаточно исследовать равновесие системы в момент перехода в предельное пластическое состояние, т. е. в так называемое предельное равновесие. Сложность состоит в том, что конкретный механизм перехода системы в предельное пластическое состояние заранее неизвестен. Поэтому приходится рассматривать все кинематически возможные варианты перехода к предельному равновесию и для каждого из них вычислять предельную нагрузку. Фактически будет иметь место тот вариант предельного состояния, которому соответствует минимальное значение предельной нагрузки.

В данной задаче возможны три варианта предельного равновесия конструкции: 1) текут стержни 1 и 3; 2) текут стержни 2 и 3 и, наконец, 3) текут стержни 2 и 1.

В качестве примера рассмотрим два варианта предельного пластического состояния в нашей задаче. Согласно первому варианту допустим, что напряжения в стержнях 1 и 3 равны , а стержень 2 работает упруго. Для определения направления усилий в стержнях 1 и 3 построим план перемещений, используя те же правила построения плана перемещений, которые описаны при решении задач № 3 и 5. Поскольку упругие деформации стержня 2 много меньше пластических деформаций стержней 1 и 3, то при построении плана перемещений стержень 2 можно считать абсолютно жестким. Под действием нагрузки жесткий стержень 2 повернется вокруг шарнира А, и этот поворот вызовет укорочение стержня 1 на и удлинение стержня 3 на (рис. 6, а). Соответствующий плану перемещений план сил для первого варианта перехода в предельное состояние показан на рис. 6, б.

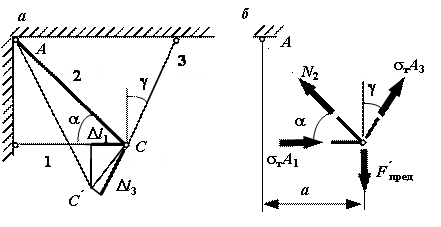
Рис.6

Чтобы неизвестное усилие N₂ не входило в уравнение, в качестве условия предельного равновесия выберем уравнение "сумма моментов относительно шарнира равна нулю" (см. рис. 6, б):

; .

Из этого уравнения при , найдем .

Во втором варианте предельного пластического состояния напряжения в стержнях 2 и 3 равны , а первый стержень работает в упругой стадии. Планы сил и перемещений показаны на рис. 7.

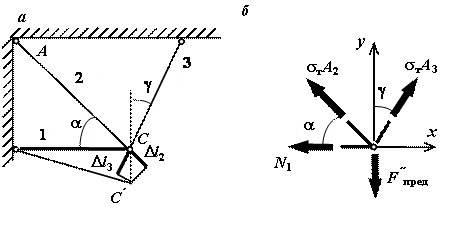
Рис.7

Запишем уравнение предельного равновесия для узла С (такое уравнение равновесие, в которое не входит неизвестное усилие N₁):

; .

Отсюда .

Аналогично можно определить предельную нагрузку для третьего варианта, в котором пластически деформироваться будут стержни 1 и 2. Фактической предельной нагрузкой будет минимальное значение из трех полученных. В нашей задаче это (первый вариант предельного состояния), что совпадает со значением, найденным ранее расчетом по упругопластической стадии.

Надо отметить, что число кинематически возможных вариантов предельного состояния может уменьшиться, если ось какого-либо стержня совпадает с линией действия нагрузки (в этом случае поворота этого стержня не происходит и механизма не образуется).

Допускаемое значение нагрузки определяем как отношение предельного значения нагрузки к коэффициенту запаса прочности n.

IV. Определение остаточных напряжений

Процесс нагружения конструкции в упругой и упругопластической стадиях, рассмотренный в пп. I и II, можно отобразить на диаграмме в осях (рис.8). Характерные точки этой диаграммы получены по соответствующим зависимостям для трех стержней конструкции.

Рис.8. Зависимость между напряжениями и нагрузкой

в процессе увеличения и уменьшения

нагрузки для стержней:

Рассмотрим процесс полной разгрузки системы из положения предельного равновесия (на диаграмме это соответствует вертикальной прямой с абсциссой ). Процесс разгрузки можно трактовать как наложение на существующие напряжения напряжений от отрицательного приращения нагрузки. Закон изменения последних определяется упругим решением задачи до тех пор, пока величина напряжения в одном из стержней не достигнет , поэтому линии разгрузки каждого стержня будут направлены параллельно линиям упругого нагружения (левый участок диаграммы). Если одно из напряжений при разгрузке достигнет величины (как это имеет место в нашем случае), то законы изменения напряжений станут соответствовать упругопластической стадии, а их графики будут параллельны соответствующим линиям нагружения (правый участок диаграммы).

Зависимости можно записать, пользуясь уравнением прямой с известным угловым коэффициентом, проходящей через заданную точку:

где - угловой коэффициент прямой линии нагружения, параллельной рассматриваемой линии разгрузки; и - начальные параметры (напряжение и нагрузка в начале участка). В нашем случае , для стержней 1 и 3, а для стержня 2 .

Запишем эти зависимости непосредственно после начала разгрузки:

Напряжение , как легко вычислить, достигнет значения при снижении нагрузки до . При этом напряжения в остальных стержнях будут , .

Пользуясь найденными значениями как начальными параметрами, запишем зависимости для напряжений на втором участке разгрузки, проходящей в упругопластической стадии:

При полной разгрузке () получаем следующие значения остаточных напряжений: , , . В заключение следует проверить равновесие узла при полученных значениях остаточных напряжений.

Монтажные напряжения в стержневых системах при растяжении-сжатии

Пример 25.

Определить напряжения, возникающие в упругих элементах системы после сборки, если стержень 1 изготовлен короче проектной длины на = 0,5 мм. Дано: А₁ = А₂ = А, а = 1м, Е = 200 ГПа.

Р е ш е н и е.

Данная система является однажды статически неопределимой (четыре неизвестных при трех уравнениях статики). Поэтому в дополнение к уравнению статики

, , (1)

необходимо составить одно уравнение совместности деформаций. Из подобия треугольников ВВ₁В₂ и СС₁С₂ имеем ВВ₂/СС₂ =ВВ₁/СС₁ или . Заменяя деформации через усилия в стержнях, получим дополнительное уравнение

или . (2)

Решая совместно уравнения (1) и (2), найдем усилия в стержнях , , 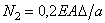а по ним и искомые напряжения

МПа;

МПа.

Пример 26.

В конструкции из трёх стержней длина среднего стержня меньше проектной длины на = 2 мм (рис.1). Определить усилия и напряжения в стержнях после сборки конструкции. Принять: F₁= F₃ = 20 см² = 2∙10^-3 м²; F₂ = 60 см² = 6∙10^-3 м²; Е₁ = Е₃ = 2∙10⁵ МПа; Е₂ = 1∙10⁵ МПа; F₂ = 3F₁ = 3F₃.

Рис.1

Решение.

Рассмотрим равновесие узла А после сборки конструкции (рис. 2).

Рис.2

Получим систему сходящихся сил на плоскости, для которой можно составить два уравнение статики. Число неизвестных − три (N₁, N₂, N₃). Таким образом, данная конструкция один раз статически неопределима, т.е.

n = R − y = 3 − 2 = 1.

Составим уравнение статики

Тогда N₁ = N₃, следовательно:

Составим дополнительное уравнение совместности деформаций (удлинений стержней). Для этого рассмотрим конструкцию в деформированном состоянии (рис. 3).

Рис.3

Из имеем

Выразим отрезки АА₁ и АА₂ через деформации стержней:

Следовательно:

Выразим деформации в стержнях 1 и 2 через усилия в стержнях, при этом учтём, что второй стержень выполнен короче заданного размера на величину d.

Тогда получим:

Учитывая, что согласно , тогда:

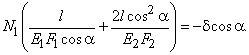
Примем = 45°; l = 1 м, тогда:

Таким образом, статическая неопределимость задачи раскрыта.

Определим напряжения в стержнях

МПа,

МПа.

Вычисленные в задаче усилия и напряжения называют монтажными или сборочными.

Температурные напряжения в стержневых системах при растяжении-сжатии

При нагревании на стержень, заделанный одним концом, увеличит свои поперечные и продольные размеры. Увеличение длины составит

где – температурный коэффициент линейного расширения. Значения коэффициентов линейного расширения для некоторых материалов приведены в справочных таблицах.

Если система представляет собой статически определимую систему, то изменение температуры не вызовет в ней никаких внутренних усилий.

При нагревании на стержня, заделанного двумя концами, возникнет нормальная сила, так как заделка препятствует удлинению стержня. Для определения нормальных усилий применяется обычный метод расчета статически неопределимых систем.

Пример 27.

Пусть дана система, представленная на рисунке. Предположим, что все стержни выполнены из одного материала и имеют одинаковую площадь поперечного сечения А. Примем, что внешняя нагрузка отсутствует, т.е. F = 0, но средний стержень нагрет на величину .

Решение.

Из симметрии конструкции следует, что нормальные силы в крайних стержнях одинаковы (N_B = N_C). Предположим, что все стержни растянуты. Рассечем мысленно все стержни и составим уравнение равновесия в виде суммы проекций сил на вертикальную ось:

(а)

Таким образом, имеем две неизвестные нормальные силы, но одно уравнение равновесия. Задача является один раз статически неопределимой. При составлении дополнительного уравнения примем во внимание, что абсолютные удлинения всех трех стержней одинаковы:

или

Абсолютные удлинения крайних стержней возникают от продольной нормальной силы, а абсолютное удлинение среднего стержня равно сумме его температурного удлинения и упругой деформации от продольной силы N_D. Приравняв абсолютные удлинения

, находим .

Подставляя полученное выражение в уравнение равновесия (а), определяем: и Следовательно, в крайних стержнях будут действовать растягивающие нормальные силы, а в среднем – сжимающая нормальная сила.

Если на стержневую систему (см. рисунок) действует также и внешняя сосредоточенная сила то определив нормальные силы в стержнях, возникающие от этой силы, используем принцип независимости действия сил и просто складываем результаты двух расчетов: от температурного воздействия и от внешней сосредоточенной силы.

Например, от внешней силы F в стержнях возникнут внутренние нормальные усилия . При нагревании среднего стержня на величину в стержнях возникают, согласно проведенного выше расчета, нормальные усилия

При одновременном действии внешней силы F и нагреве среднего стержня на в стержнях будут следующие нормальные усилия:

Пример 28.

Определить напряжения, возникающие в упругих элементах системы (см. рис.), если после монтажа температура увеличилась на °C.

Дано: А₁/А₂ = 2, Е = 200 ГПа, .

Р е ш е н и е.

Данная система является однажды статически неопределимой.

Уравнение статики , ,

или , откуда . (1)

Уравнение совместности деформаций

или .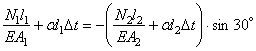

Переходя от усилий к напряжениям, получим

. (2)

Решая совместно (1) и (2), найдем температурные напряжения

МПа.

Пример 29.

Требуется:

1.Определить допускаемое значение силы [P] из расчета на прочность стержней (рис.1,а), если допускаемое напряжение =16 кН/см². Брус АВ считать абсолютно жестким.

2. Определить напряжение в стержнях, если второй стержень нагрет на , при этом считать, что сила P отсутствует. Модуль упругости материала стержней , коэффициент линейного расширения .

3. Вычислить напряжения в стержнях при совместном действии допускаемой силы [P] и нагрева.

а) б) в)

Рис.1

Решение.

1.Применяя метод сечений, рассмотрим равновесие отсеченной части (рис. 1.б). В стержнях возникают продольные силы и , в шарнире А – опорные реакции и . Усилие считаем сжимающим, а - растягивающим. Если после решения усилия получится отрицательным, то его направление следует поменять на противоположное.

Для решения задачи не надо определять реакции в шарнире А, потому что в качестве условия равновесия составим следующее уравнение:

(1)

Имеем следующее уравнение статики

(2)

Из уравнения (2) следует, что рассматриваемая система один раз статически не определимая, поэтому необходимо составить уравнение перемещений.

После приложения нагрузки брус АВ останется прямым и займет положение АВ₁ (рис.1, в). При этом перемещение шарниров В и С произойдет по дугам радиусов АВ и АС. Ввиду малости деформаций стержней эти дуги можно заменить прямыми ВВ₁ и СС₁. Точки крепления стержней с брусом АВ получат перемещения по дугам радиусов . Эти дуги также заменяются отрезками касательных (рис.1, в).

Так как стержень является наклонным, то получаем

Из подобия треугольников АВВ₁ и АСС₁ имеем

Используя закон Гука, получаем:

(3)

Решая систему уравнений (2) и (3), находим усилия в стержнях

Напряжения в стержнях равны

Сравнивая полученные напряжения, приходим к выводу, что и .

Условие прочности системы имеет вид:

2. При нагревании второго стержня на в нем возникает сжимающее усилие (рис.2, а), так как брус АВ, скрепленный с первым стержнем, будет препятствовать свободному температурному удлинению (рис. 2, б).

а) б)

Рис.2

При температурном удлинении второй стержень, воздействуя на брус АВ, вызывает сжатие первого стержня. Составим уравнение равновесия

(4)

Уравнение перемещений имеет вид:

(5)

Первый стержень не нагревается, поэтому его деформация Второй стержень испытывает воздействия температуры и его деформация такова:

Подставляя эти выражения в (5), получим:

или (6)

Решая систему уравнений (4) и (6), находим усилия

Напряжения в поперечных сечениях стержней

3. Напряжения в стержнях от действия силовой нагрузки [Р]=29,8 кН будут равны

Напряжения при совместном действии силы [Р] и нагрева определяются алгебраическим суммированием результатов вычисления напряжений

Напряжение в первом стержне .

Определим процент перегрузки.

Перегрузка допускается не более 5%. Стержень перегружен.

Пример 30.

Для схемы, изображенной на рис.1 необходимо:

Рис.1

1) Определить площадь поперечного сечения стержней при действии силы F и подобрать угловую равнополочную или неравнополочную сталь, при условии, что поперечное сечение одного из стержней в два раза больше, чем другого.

2) Определить напряжения в стержнях:

- от действия силы F;

- от неточности монтажа, если считать, что один из стержней выполнен короче на величину ;

- от изменения температуры.

3) Определить суммарные напряжения от действия внешних сил, от неточности монтажа и от изменения температуры.

4) Подсчитать недонапряжения или перенапряжения в стержнях.

Дано: F=100 кН, а = 1,2 м, b = 0,8 м, = 0,2 мм, = 20°С, Е = 2×10⁵МПа, = 125×10^-71/гр, = 100 МПа.

Решение.

Определим необходимую по условию прочности площадь поперечного сечения стержней.

1) Находим степень статической неопределимости.

2.1) Статическая сторона задачи

; ;

; .

2.2) Геометрическая сторона задачи (рис.2)

~ Þ

; ; ;

2.3) Физическая сторона задачи

;

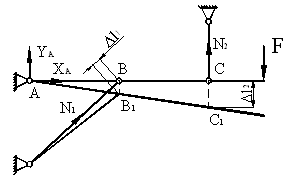
Рис.2

2.4) Синтез

Подставим выражения, полученные в физической стороне задачи, в выражения из геометрической стороны задачи и приведем подобные.

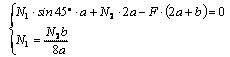
Решим совместно систему уравнений, составленную из полученного выражения для N₁ и уравнения моментов из статической стороны задачи.

2.5) Определяем площадь поперечного сечения стержней

Определим, какой из стержней нагружен сильнее.

;

Второй стержень является более нагруженным, так как , поэтому запишем для него условие прочности и определим площадь поперечного сечения.

Подбираем по справочнику угловую равнополочную сталь № 70´5 ГОСТ8509-86 (S_Т= 6,86 см²).

2.6) Определяем напряжения в стержнях от внешних сил

Первый стержень работает на сжатие, а второй – на растяжение.

3) Определим напряжения в стержнях от неточности монтажа

Будем считать, что короткий стержень выполнен короче на величину (см.рис.3).

Рис.3

3.1) Статическая сторона задачи

; ;

; .

3.2) Геометрическая сторона задачи

~ Þ

; ; ;

3.3) Физическая сторона задачи

;

3.4) Синтез

Подставим в полученное выражение данные из условия задачи и получим:

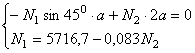
3.5) Определим напряжения в стержнях

Оба стержня работают на растяжение.

4) Определим напряжения в стержнях от изменения температуры (см. рис. 4).

Рис.4

Будем считать, что температура системы повышается. Тогда оба стержня будут удлиняться от повышения температуры. При удлинении стержней, они будут воздействовать друг на друга через недеформируемый стержень АС. Вследствие этого, в обоих стержнях будут возникать дополнительные силы сжатия.

4.1) Статическая сторона задачи

; ;

; .

4.2) Геометрическая сторона задачи

~ Þ

; ; ;

4.3) Физическая сторона задачи

;

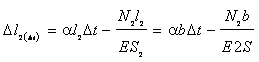4.4) Синтез

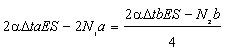
Решив уравнение, получим .

4.5) Определим напряжения в стержнях

Оба стержня работают на сжатие.

5) Определим суммарные напряжения в стержнях

6) Найдем недонапряжения или перенапряжения в стержнях

- недонапряжение

- недонапряжение.

Пример 31.

Абсолютно жесткий брус АЕ (рис. 1, а), имеющий одну шарнирно неподвижную опору С и прикрепленный в точках В, Д и Е тремя тягами из упруго-пластического материала, нагружен переменной по величине силой Р. Площадь поперечного сечения тяг F₁, F₂, F₃, модуль упругости и предел текучести материала тяг МПа, = 240 МПа. Допускаемое напряжение , где коэффициент запаса прочности n принят равным 1,5.

Требуется:

1. Найти усилия в тягах, реакцию опоры С и угловое смещение (поворот бруса вокруг точки С) как функции от величины силы Р;

2. Определить в процессе увеличения нагрузки Р такую ее величину, при которой напряжение в одной из тяг достигает предела текучести;

4. Найти величины несущей способности конструкции из расчетов по методам допускаемых напряжений и разрушающих нагрузок при одном и том же коэффициенте запаса прочности. Сопоставить результаты и сделать вывод.

Дано: м²; м²; м²; a = 2 м; b = 1 м; c = 1 м; d = 2 м; l₁ = 1 м; l₂ = 1 м; l₃ = 1,2 м.

Решение.

1. Найти усилия в тягах, реакции в опоре С и угловое смещение (поворот бруса вокруг т. С), как функции от величины силы Р. Для определения величин усилий в тягах в зависимости от Р применим метод сечений. Сделав сечение по всем тягам и приложив в местах сечений усилия N₁, N₂и N₃, возникающие в тягах, рассмотрим равновесие оставшейся части, нагруженной продольными усилиями в тягах N₁, N₂ и N₃ реакциями опоры С (R_C и H_C) и силой Р (рис. 1, б). Составив уравнения равновесия статики для оставшейся части, получим:

1) , Н_C = 0; (1)

2) , -Р + N₁+ R_C - N₂ - N₃ = 0; (2)

3) , . (3)

Рис.1

Из уравнений равновесия видно, что система дважды статически неопределима, т.к. два уравнения равновесия (2) и (3) содержат в своем составе четыре неизвестных. Поэтому для решения задачи необходимо составить два дополнительных уравнения совместности деформаций, раскрывающих статическую неопределимость системы.

Для составления дополнительных уравнений рассмотрим деформированное состояние системы (рис. 1, в), имея в виду, что брус абсолютно жесткий и поэтому после деформации тяг останется прямолинейным.

Эти дополнительные уравнения совместности деформаций получим из подобия треугольников ВСВ₁=DCD₁ и BCB₁=ECE₁:

и .

Решая эти уравнения, получим:

(4)

. (5)

Выразив деформации тяг по формуле определения абсолютного удлинения:

и подставив эти значения в уравнения (4) и (5), получим:

(6)

. (7)

Подставив найденные значения N₂ и N₃в уравнение (3) определяем величину N₁:

; N₁=0,3333P.

Зная N₁, из уравнений (6) и (7), находим N₂ и N₃:

Опорную реакцию R_C определяем из уравнения (2), подставив найденные значения N₁, N₂ и N₃:

-P + 0,333P + R_C - 0,167P - 0,833P = 0; R_C = 1,667P.

После определения величин усилий в тягах N₁, N₂, N₃ и реакции R_C необходимо проверить правильность их вычисления. Для этого составим уравнение равновесия статики :

-N₁×a - R_C(a+b) + N₂(a+b+c) + N₃(a+b+c+d)= 0;

0 = 0.

Следовательно, N₁, N₂, N₃ и R_C определены правильно.

Угловое смещение бруса (угол ), ввиду его малости, находим как тангенс угла наклона бруса АЕ:

[рад].

2. Определить в процессе увеличения нагрузки Р такую ее величину, при которой напряжение в одной из тяг достигнет предела текучести. Для вычисления величины Р, при которой напряжение в одной из тяг достигнет предела текучести s_T, определим нормальные напряжения, возникающие в тягах, учитывая то, что тяги работают на растяжение:

Полученные величины напряжений показывают, что в тяге 3 напряжение достигнет предела текучести раньше, чем в тягах 1 и 2, так как и . Поэтому, приравняв напряжение пределу текучести , определим величину Р, при которой нормальное напряжение в тяге 3 достигнет предела текучести :

кПа,

откуда

кН.

3. Определить в процессе увеличения нагрузки Р ее предельную величину, при которой напряжения в трех тягах достигнут предела текучести, реакцию опоры С и соответствующий этому предельному состоянию угол. При исчерпании несущей способности всех тяг напряжения в них достигнут предела текучести . В этом случае предельные усилия, которые возникнут в тягах, будут равны:

кH;

кH.

Предельную величину внешней нагрузки, соответствующую исчерпанию несущей способности, найдем из уравнения (3), подставив в него предельные значения , , :

; кН.

Предельную величину реакции определяем из уравнения (2):

-72 + 48 +- 24 - 48 = 0; = 96 кН.

При определении наименьшего угла поворота бруса, соответствующего предельному состоянию системы, необходимо знать, в какой из тяг текучесть наступит позже.

Полученные величины напряжений (см. п. 2) показывают, что в тягах 1 и 2 напряжения достигнут предела текучести одновременно, но позже, чем в тяге 3. Поэтому предельный угол поворота бруса определяем для момента перехода материала тяг 1 и 2 в пластическое состояние:

рад,

или

рад.

4. Найти несущую способность из расчетов по методам допускаемых напряжений и разрушающих нагрузок при одном и том же коэффициенте запаса прочности. Сопоставить результаты и сделать вывод. Из предыдущих расчетов (см. п. 2) видно, что текучесть материала раньше появится в тяге 3, т.к. и . Поэтому для определения величины грузоподъемности из расчета по методу допускаемых напряжений приравниваем напряжение в этой тяге к допускаемому напряжению:

кПа,

кH.

Несущая способность конструкции из расчета по методу разрушающих нагрузок получим путем деления ранее полученного значения P_ПР = 72 кН на коэффициент запаса n₁ = 1,5:

кH.

Сравнивая полученные величины, видим, что несущая способность из расчета по методу разрушающих нагрузок больше несущей способности из расчета по методу допускаемых напряжений на , что подтверждает известное положение о том, что метод допускаемых напряжений, в отличии от метода разрушающих нагрузок, не позволяет определить полную несущую способность системы. Это объясняется тем, что для статически неопределимых систем, переход одного элемента в пластическую стадию работы, как правило, не означает наступления предельного состояния. Переход системы в предельное состояние отождествляется с превращением ее из неизменяемой в геометрически изменяемую систему. Известно, что в статически неопределимой системе разрушение “лишних связей” не превращает ее в геометрически изменяемую. Так как реальные сооружения чаще всего представляют собой многократно статически неопределимые системы, материал которых обладает свойством пластичности, поэтому метод предельного равновесия имеет важное значение для раскрытия истинных резервов их несущей способности.

Онлайн-калькулятор "Расчет прочности при растяжении-сжатии"

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00