Главная

Лекция 7 (продолжение). Задачи для самостоятельного решения

Содержание

Расчет стержней при внецентренном сжатии-растяжении

Расчет балок при косом изгибе

Задача 1.

Защемленная одним концом двутавровая балка №24а длиной 1,4 м, нагружена на собственном конце сосредоточенной силой F, прогнулась под силой на 3 мм. Направление прогиба совпала с биссектрисой угла между главными осями инерции поперечного сечения балки. Определить величину и направление силы F, а также наибольшее растягивающее напряжение в балке.

Ответ: F=17,65 кН; .

Задача 2.

Направление полного прогиба балки прямоугольного сечения вх2в составляет с главными осями сечения рад. Определить положение плоскости изгибающего момента.

Ответ: α=1,326 рад (с осью х).

Задача 3.

При установке на опоры I №60, предназначенного для работы на изгиб в вертикальной плоскости, совпадающей с плоскостью стенки, была допущена ошибка, и стенка двутавра отклонилась от вертикали на угол 3⁰. Определить связанное с этим увеличением наибольших нормальных напряжений и полного прогиба двутавра.

Ответ: Напряжения увеличились на 74%, полный прогиб – на 154%.

Задача 4.

Какое положение займет нейтральный слой в баке прямоугольного поперечного сечения, если плоскость действия нагрузки будет совпадать с одной из диагональных плоскостей?

Ответ: Совпадает с другой диагональной плоскостью.

Задача 5.

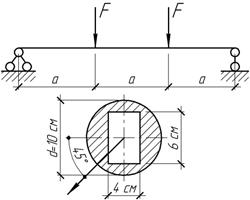
Консоль нагружена на свободном конце силой F. Поперечное сечение балки имеет две оси симметрии, моменты инерции относительно которых равны 250 см⁴ и 3400 см⁴. Направление силы F составляет с осями симметрии сечения угол, равный рад. Вычислить угол наклона нулевой линии к оси максимальной жесткости сечения.

Ответ: 1,497 рад.

Задача 6.

Стальная консольная балка двутаврового поперечного сечения (двутавр № 24) длиной 1 м загружена сосредоточенной вертикальной силой F = 40 кН. Найти максимальное нормальное напряжение в балке и вычислить прогиб конца консоли, если модуль упругости Е =2∙10⁵ МПа. Определить, как изменятся напряжения и прогиб балки, если сила F отклонится от вертикали на угол α= 5^о.

Ответ: при прямом изгибе σ_max= 138,5 МПа; w = 0,193 см; при косом изгибе напряжения и прогиб возрастают в 1,7 раза.

Задача 7.

При установлении опоры двутавра № 60 была допущена ошибка и стенка двутавра отклонилась от вертикали на угол равный 1^о. Определить связанное с этим увеличение нормальных напряжений и полного прогиба двутавра.

Ответ: напряжения увеличились на 20%, полный прогиб на 30%.

Задача 8.

Балка прямоугольного сечения 4х24 см была рассчитана для работы в вертикальной плоскости. Однако в процессе эксплуатации оказалось, что плоскость действия нагрузки может отклоняться от вертикали до 5⁰. Спрашивается, гарантирует ли безопасную работу конструкции принятый при расчете коэффициент запаса П=1,5?

Задача 9.

Ответ: 1,497 рад.

Задача 10.

Направление полного прогиба балки прямоугольного сечения bx2b составляет с главными осями сечения угол рад. Определить положение плоскости изгибающего момента.

Ответ: α=1,326 рад (с осью х).

Задача 11.

При установке на опоры двутавра № 60, предназначенного для работы на изгиб в вертикальной плоскости, совпадающей с плоскостью стенки, была допущена ошибка, и стенка двутавра отклонилась от вертикали на угол 3⁰. Определить связанное с этим увеличением наибольших нормальных напряжений и полного прогиба двутавра.

Ответ: Напряжения увеличились на 74%, полный прогиб – на 154%.

Задача 12.

Защемленная одним концом двутавровая балка № 24а длиной 1,4 м, нагруженная на свободном конце сосредоточенной силой F, прогнулось под силой на 3 мм. Направление прогиба совпало с биссектрисой угла между главными осями инерции поперечного сечения балки. Определить величину и направлении силы F, а также наибольшее растягивающее напряжение в балке.

Ответ: F=17,65 кН, (к вертикали),

Задача 13.

Балка прямоугольного сечения bxh подвергается косому изгибу моментами М_х и М_у. Определить из условия прочности отношение сторон сечения m=h/b, при котором балка имеет минимальный вес.

Ответ: m=h/b=М_х/М_у.

Задача 14.

Какое положение займет нейтральный слой в балке прямоугольного поперечного сечения, если плоскость действия нагрузки будет совпадать с одной из диагональных плоскостей?

Ответ: Совпадает с другой диагональной плоскостью.

Задача 15.

Для балки прямоугольного сечения плоскость действия нагрузки направлена по диагонали прямоугольника. Докажите, что нейтральная линия совпадает с другой диагональю прямоугольника.

Задача 16.

Балка квадратного сечения, защемлена одним концом, на свободном конце нагружена силой F. В первом случае сила направлена параллельно стороне квадрата, а во втором совпадает с его диагональю. Как изменится величина силы F при переходе от первого варианта ко второму при условии, что наибольшие нормальные напряжения в обоих случаях одинаковы.

Задача 17.

Чугунная балка треугольного поперечного сечения, шарнирно опертая по концам, в плоскости, параллельной стороне АВ, изгибается сосредоточенной силой F=24 кН, приложенной посредине пролета l=1.8 м. определить необходимые размеры поперечного сечения балки, если

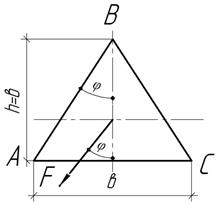
Ответ: в=18 см

Задача 18.

Определить величину допускаемого момента, плоскость которого наклонена к вертикали на угол φ=20⁰, если

Ответ: М_adm=40 кНм

Задача 19.

Проверить прочность стальной балки, если F=24 кН, а=1 м, в=8 см, .

Ответ:

Задача 20.

Подобрать размеры поперечного сечения балки и построить эпюру нормальных напряжений в опасном сечении. Найти также величину и направление полного прогиба сечения С. Дано: F=6 кН; Е=10 ГПа; а=1 м; h/в=2;

Ответ: в=13 см; .

Задача 21.

Проверить прочность и жесткость стальной балки, если и [f]=l/400.

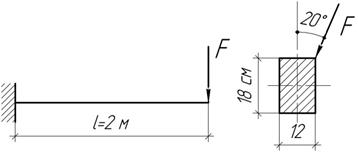
Ответ: f=5 мм; .

Задача 22.

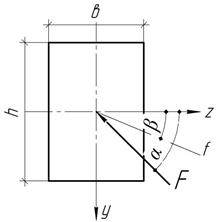
При косом изгибе балки прямоугольного сечения tgα=4tgβ, где α и β – углы, определяющие плоскости нагрузки и перемещений соответственно. Каким должно быть отношение h/в?

Задача 23.

Проверить прочность и жесткость стальной балки, если

Ответ:

Задача 24.

Для балки из I №55 определить величину допускаемой нагрузки из условия прочности и жесткости, если

Ответ:

Задача 25.

Балка прямоугольного сечения вхh подвергается косому изгибу моментами М_х и М_у. Определить из условия прочности отношение сторон сечения m=h/в, при котором балка имеет минимальный вес.

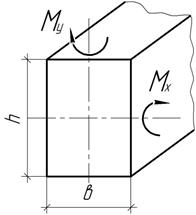
Ответ: m=h/в=М_х/М_у

Задача 26.

Для деревянной балки требуется определить величины допускаемых сил F и положение нулевой линии в опасном сечении, а также величину и направление полного прогиба свободного конца, если Е=10 ГПа,

Ответ: F=1,6 кН; f=13,34 мм;

Задача 27.

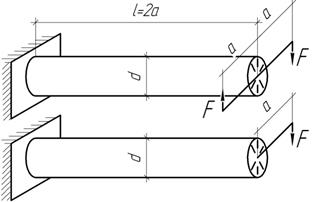
Консольные балки из двутавра и швеллера, имеющие одинаковую площадь поперечного сечения и длину, нагружены силой F под углом φ=18⁰ к вертикали. В балке из швеллера сила приложена в центре изгиба. Установите, какая из балок обладает большей несущей способностью и выполните количественную оценку.

Ответ: на 8,7% выше у швеллера.

Задача 28.

Определить допускаемое значение силы F, если При найденном значении силы построить эпюру нормальных напряжений в опасном сечении.

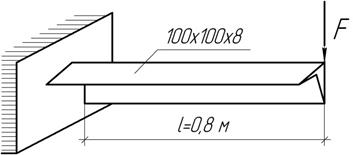
Задача 29.

Для балки заданного сечения известно положение плоскости действия внешней нагрузки. Определите положение нейтральной линии и плоскости кривизны оси балки.

Задача 30.

В результате изгиба балки под действием плоской системы сил центр тяжести некоторого сечения переместился в указанном направлении. Определите положение нейтральной и силовой линии для этого сечения.

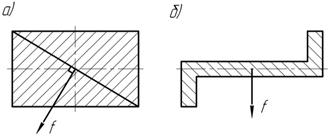
Задача 31.

При каком положении силы F консольная балка не испытывает косой изгиб, если ее сечение составлено из: а) квадрата и равновеликого ему равностороннего треугольника; б) двух одинаковых прямоугольников?

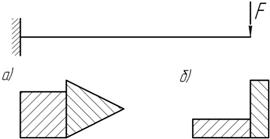
Задача 32.

Для опасного сечения балки, испытывающей косой изгиб, напряжение в точке К равно нулю. В каких точках возникают наибольшие напряжения?

Задача 33.

Стальной уголок (равнобокий а и неравнобокий б) нагружены по концам изгибающими парами, действующими в плоскости, параллельной одной из полок. Установите положение опасных точек и постройте качественно (без вычислений) эпюру нормальных напряжений.

Задача 34.

Балка квадратного сечения bxb длиной l шарнирно оперта по концам и нагружена моментами М и погонной нагрузкой интенсивности q. При каком значении момента М во всех сечениях по длине балки наибольшие напряжения будут одинаковы?

Задача 35.

Какой из трех видов нагружения бруса, выполненного из пластичного материала, является более опасным?

Задача 36.

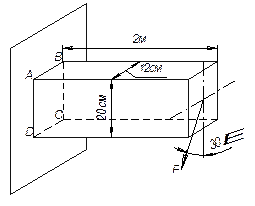
Деревянная балка длиной 2 м, имеющая прямоугольное поперечное сечение 12х20 см, защемлена одним концом и нагружена сосредоточенной силой F=2,4 кН на другом конце. Нагрузка лежит в плоскости поперечного сечения балки и проходит через его центр тяжести (см. рисунок). Построить эпюры нормальных напряжений по сторонам защемленного сечения и определить полный прогиб свободного конца балки.

Ответ: σ_A=+0,2 Мпа; σ_B=+10,2 Мпа; σ_С=-0,2 Мпа; σ_D=-10,2 Мпа; f=13,1 мм.

Задача 37.

Для балки, лежащей на двух опорах и загруженной тремя вертикальными сосредоточенными силами F₁ = F₃ = 10 кН, F₂ = 20 кН и равномерно распределенной горизонтальной нагрузкой q = 24 кН/м, требуется подобрать прямоугольное поперечное сечение с отношением сторон h = 1,5b. Пролет балки равен 1 м, R_y = 150 МПа, γ_с = 1 (см. рис.).

Ответ: b = 6 см, h = 9 см.

Задача 38.

Балка прямоугольного поперечного сечения b×h = 0,18м×0,24м нагружена так, как показано на рисунке. Найти наибольшее нормальное напряжение, если сила F = 60 кН, пролет балки l = 3 м, угол между линией действия силы F и вертикальной осью α = 30^o.

Подпись: h

Ответ: σ_max = 35,5 МПа.

Задача 39.

Определить наибольшие (по абсолютной величине) нормальные напряжения в балке пролетом 2 м, опирающейся на шарнирные подвижную и неподвижную опоры и несущую посередине пролета сосредоточенный груз F = 6кН. Сечение балки с прямоугольным отверстием показано на рис. 1.

У к а з а н и е Вначале необходимо определить положение нейтральной оси.

Балка прямоугольного сечения изгибается моментом М = 10 кНм (рис. 2). Найти точки с наибольшими нормальными напряжениями и вычислить эти напряжения.

Балка двутаврового сечения №20 свободно опирается на прогоны, наклоненные под углом 30^о к горизонтали (рис.3). Расстояние между осями прогонов 4 м. Балка посередине нагружена вертикальной сосредоточенной силой F = 8 кН. Пренебрегая собственным весом балки, определить напряжения в точках a, b, c, d и угол наклона β нейтральной оси сечения балки к главной оси z.

Подпись: h=6 см

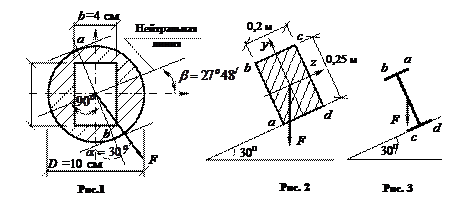
Ответ к рис.1: σ_max= 35,1 МПа.

Ответ к рис.2: σ_max=σ₍_a)= 7,15 МПа; σ_min=σ₍_c)= –7,15 МПа.

Ответ к рис.3: σ₍_a)= –210,9 МПа; σ₍_b)=–135,5 МПа; σ₍_c)= 210,9 МПа; σ₍_d) =135,5 МПа; β = 83^о48^/.

Задача 40.

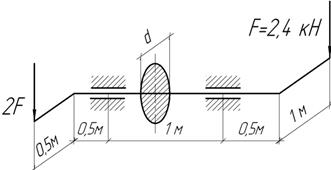
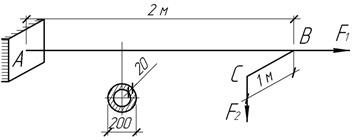
Стальная консольная балка двутаврового поперечного сечения длиной l=2 м изгибается силой F=8 кН, приложенной к ее свободному концу (см. рис.). Пренебрегая собственным весом балки, подобрать номер двутаврового профиля и определить прогиб свободного конца, если α= 30^o, R_y = 140 МПа, γ_c= 1 и модуль упругости Е = 2∙10⁵МПа.

У к а з а н и е. Для двутаврового сечения при предварительном подборе принимают W_y / W_z = 8–10.

Ответ: двутавр № 36; прогиб w = 1,03 см.

Задача 41.

Проверить прочность и жесткость стальной балки, если [σ]=140 МПа и [f]=l/400.

Ответ: а) мм =[f]; б) мм =[f].

Задача 42.

Подобрать размеры поперечного сечения деревянной балки и построить эпюру нормальных напряжений в опасном сечении балки, если [σ]=15 МПа и [τ]=3 МПа, q=3 кН/м.

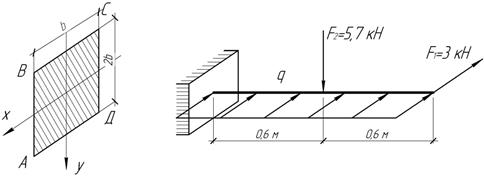
Ответ: b=12 см,

Задача 43.

Шарнирно опертый по концам швеллер нагружен равномерно распределенной нагрузкой интенсивности q=5 кН/м. определить нормальные напряжения в точках А, В, С и Д опасного сечения балки, а также величину и направление наибольшего прогиба, если длина балки l=4 м.

Ответ: (к оси х).

Задача 44.

Деформации в точках А и В стальной балки по направлениям баз датчиков, определенные с помощью электротензометрической установки, равны соответственно Найти величину и направление силы F, приложенной посредине балки.

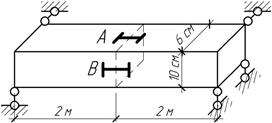
Ответ: F=10 кН, φ=30⁰ (к вертикали).

Задача 45.

Чугунная балка треугольного поперечного сечения, в плоскости, параллельной стороне АВ, изгибается сосредоточенной силой F=24 кН, приложенной посредине пролета l=1,8 м. определить необходимые размеры поперечного сечения балки, если и

Ответ: b=18 см.

Задача 46.

Подобрать сечение балки и определить полный прогиб ее на свободном конце по величине и направлению, если [σ]=10 МПа, Е=10 ГПа, F₁=0,8 кН; F₂=1,65 кН.

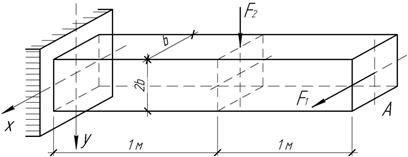
Ответ: b=9 см, см; (к оси х).

Задача 47.

Проверить прочность балки и построить эпюру нормальных напряжений в опасном сечении, если F=14 кН, а=1 м, [σ]=160 МПа.

Ответ: МПа (прочность обеспечена), (к оси х).

Задача 48.

Консольные балки из двутавра и швеллера, имеют одинаковую площадь поперечного сечения и длину, нагружены силой F под углом φ=18⁰ к вертикали. В балке из швеллера сила приложена в центре изгиба. Установите, какая из балок обладает большей несущей способностью и выполните количественную оценку.

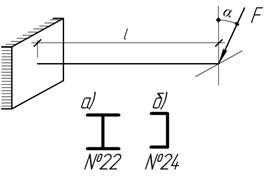
Ответ: На 8,7% выше у швеллера.

Задача 49.

Подобрать сечение балки и определить положение нейтральной оси в опасном сечении, если q=2,3 кН/м, F=6 кН, [σ]=70 МПа, а=0,5 м; φ=30⁰,

Ответ: d=10 см, к оси х.

Задача 50.

Установите наибольшее отклонение от вертикали силы F=80 кН, при котором еще сохраняется прочность стальной балки, если [σ]=150 МПа. При найденном значении φ определите деформации в направлении без тензометров Т₁ и Т₂.

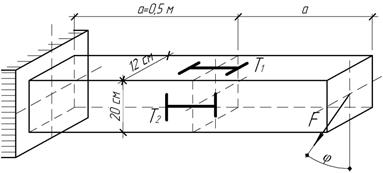
Ответ:

Задача 51.

Для балки двутаврового профиля № 55 определить величину допускаемой нагрузки из условия прочности и жесткости, если [σ]=160 МПа, [f]=1 см, а=1 м, φ=30⁰.

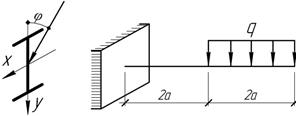
Ответ: [q]=2 кН/м (из условия жесткости).

Задача 52.

Проверить прочность деревянной балки и построить эпюру нормальных напряжений на плоскости и в аксонометрии для опасного сечения. Найти также величину и направление полного прогиба сечения С. Дано: F=6,4 кН, [σ]=10 МПа, Е=10 ГПа, а=1 м.

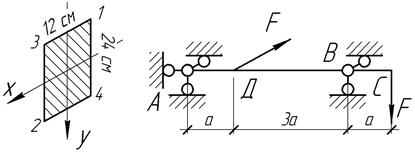
Ответ:

Задача 53.

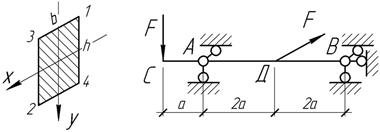
Ответ: .

Задача 54.

Определить допускаемое значение силы F и построить эпюру нормальных напряжений для опасного сечения. Найти также величину и направление полного прогиба сечения С. Дано: [σ]=11 МПа, Е=10 ГПа, а=1 м.

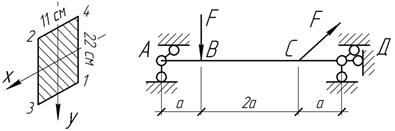
Ответ:

Задача 55.

Проверить прочность стальной балки, если F=24 кН, [σ]=150 МПа, а=1 м, b=8 см.

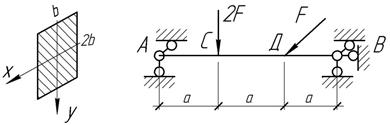
Ответ:

Расчет стержней при внецентренном сжатии-растяжении

Задача 1.

Как изменятся размеры ядра сечения, если круглое сплошное сечение диаметром D заменить трубчатым с наружным диаметром D и внутренним диаметром d.

Ответ: радиус ядра сечения увеличится в раз.

Задача 2.

Определить эксцентриситет продольной силы, при котором нормальные напряжения в крайних волокнах образца круглого сечения диаметром d отличаются от среднего значения напряжений не более, чем на 5%.

Ответ: е<0,0125d.

Задача 3.

Круглая цилиндрическая башня, имеющая высоту h, внутренний диаметр и наружный , слегка отклоняется от вертикали. Полагая, что на башню действует только ее собственный вес, определить максимальный угол φ отклонения от вертикали, при котором в башне нигде не возникают растягивающие напряжения. Выполнить количественную оценку, приняв h=5 м,

Ответ:

Задача 4.

Для круглого поперечного сечения с радиусом R ядро сечения представляет собой соосный круг меньшего радиуса r = R/4. Доказать, что при приложении к круглому поперечному сечению внешней силы на расстоянии, равном радиусу R от центра кругов, нейтральная линия коснется контура ядра сечения.

Задача 5.

Построить ядро сечения для прямоугольника с высотой h и шириной b. Главная ось z направлена параллельно стороне с высотой h.

У к а з а н и е . Учесть, что предельными будут такие положения нейтральных линий, при которых эти линии совпадут с контурами сечения.

Ответ: ядро сечения – ромб с большой диагональю, расположенной на оси z и равной h/3, малой – на оси y и равной b/3.

Задача 6.

От какого вида напряжений (растяжение или сжатие) произойдет разрушение бетонной колонны, если сжимающая ее сила будет приложена: а) в точке А? б) в точке В? Предел прочности бетона при сжатии в шесть раз больше предела прочности при растяжении. Зависимость между σ и ε считать линейной вплоть до разрушения.

Ответ: а) сжатие; б) растяжение.

Задача 7.

Листовой элемент рамы прямоугольного поперечного сечения, имеющее внецентренно-расположенное сквозное отверстие, нагружен растягивающими силами F=300 кН. Найти наибольшее растягивающие напряжение в ослабленном сечении.

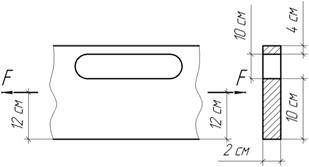
Ответ: 157 Мпа.

Задача 8.

Проверить прочность нижней части бетонного столба прямоугольного поперечного сечения, если F=6 кН,

Ответ:

Задача 9.

Колонны с поперечным сечением, изображенным на рисунке, сжаты продольной силой, приложенной в точке А. Определить, во сколько раз максимальное нормальное напряжение в данном случае меньше того, которое возникло бы в колонне, если бы толщина ее стенок везде была одинаковой и равной 6 см.

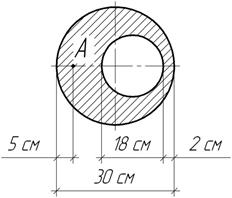
Ответ: в 1,15 раза.

Задача 10.

Жестко заделанный нижним концом короткий брус таврового поперечного сечения нагружен сжимающими силами F и 2F. Определить значение параметра сил F из условия, чтобы наибольшие напряжения не превышали: на сжатие 100 МПа, на растяжение 40 МПа.

Ответ: 394 кН.

Задача 11.

Полоса толщины t=10 мм растягивается силой Р=50 кН с эксцентриситетом е=в/4. определить ширину в при допускаемом напряжении

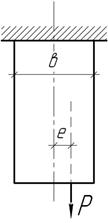
Ответ: в=7,8 см.

Задача 12.

К горизонтально расположенной крестовине, жестко скрепленной со стальной трубой диаметром d=50мм и толщиной t=2мм, симметрично подвешены четыре одинаковых груза G=1 кН. Определить наибольшее напряжение в трубе при четырех грузах, а также в том случае, когда один из грузов снят.

Ответ:

Задача 13.

Короткая чугунная колонна кольцевого поперечного сечения жестко заделана нижним концом. На свободном конце она нагружена продольными сжимающими силами в точке А F_А=800 кН и в точке В F_В=400 кН. Определить наибольшее сжимающие напряжение и построить эпюру нормальных напряжений для поперечного сечения колонны.

Ответ:

Задача 14.

Двутавровая стойка поддерживает платформу весом G=120 кН, на которую действует две силы F=80 кН. Определить необходимый номер двутавра при загружении платформы двумя силами или одной из них, если а=1 м, [σ]=140 МПа.

Ответ: двутавр № 36.

Задача 15.

Найти координаты точки приложения сжимающей силы F для короткой двутавровой колонны из условия, что нулевая линия занимает положение, показанное на рисунке.

Ответ:

Задача 16.

Колонны круглого и прямоугольного сечения нагружены сжимающими силами в точках А. При этом сжимающие напряжения в этих точках оказались одинаковыми. Сравните напряжения в точках В.

Ответ:

Задача 17.

Определить напряжения в опасном сечении растянутого стержня с местным ослаблением, показанным на рисунке. А=40 мм, F=10 кН.

Ответ:

Задача 18.

Определить диаметр круглой чугунной колонны, нагруженной силой F=16 кН, если допускаемое напряжение на растяжение для чугуна равно

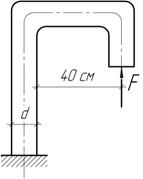
Ответ: d=125 мм.

Задача 19.

Определить допускаемую глубину х выреза в полосе сечения 60х10 мм, растягиваемой по оси силой F=15 кН. Допускаемое напряжение

Ответ: х=23,5 мм.

Задача 20.

Нормальное напряжение в точке А сжатого бруса равно 1,2 МПа (растяжение), а в точке В равно нулю. Чему равно напряжение в точке С? F- точка приложения силы.

Ответ:

Задача 21.

Как изменится максимальное напряжение в брусе квадратного сечения, если сила, действующая вдоль оси бруса, параллельно переместится на контур поперечного сечения в точку А? В точку В?

Ответ:

Задача 22.

Найти необходимую толщину полосы t, если F=90 кН, [σ]=100 МПа.

Ответ: t=1 см.

Задача 23.

Колонна квадратного сечения 60х60 см нагружена вертикальной силой F. Где надо приложить силу F, чтобы напряжения в точке А равнялись нулю?

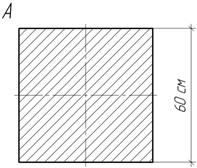
Задача 24.

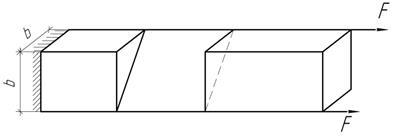
Найти в правом торцевом сечении точку приложения третьей силы F той же величины и направления, при которой в ослабленном сечении напряжения будут распределяться равномерно.

Задача 25.

Для колонны заданного сечения, испытывающей внецентренное сжатие, определите положение нейтральной линии и постройте качественно эпюру нормальных напряжений.

Задача 26.

Стальная полоса прямоугольного сечения имеет одностороннюю выточку глубиной на ¼ высоты. Повысится ли несущая способность полосы, если сделать аналогичную выточку и с другой стороны? Обоснуйте ваше заключение.

Задача 27.

Кирпич марки А более тяжелый, чес кирпич марки В. Из кирпича какой марки лучше всего делать высокую заводскую трубу, подверженную как действию собственного веса, так и значительной ветровой нагрузки?

Задача 28.

Сплошной стержень квадратного сечения bxb нагружен продольными силами F. Насколько изменятся наибольшие напряжения, если в средней части стержня сделать врубку, как показано на рисунке?

Задача 29.

При каком значении у показания тензометра Т, установленного на верхней грани стержня квадратного сечения в процессе нагружения меняться не будут?

Задача 30.

Измеренная относительная деформация верхнего волокна нагруженного стержня равна ε=0,002. Каково абсолютное удлинение центрального волокна?

Задача 31.

Опорный башмак шириной передает усилие F, которое распределяется по торцу колонны по закону треугольника. Определите длину башмака с, обеспечивающую минимально возможное контактное давление р при условии, что в поперечных сечениях колонны возникают только напряжения сжатия.

Задача 32.

Проверить прочность нижней части бетонного столба, имеющей прямоугольное поперечное сечение 18х20 см (см. рисунок). Допускаемое напряжение на растяжение равно 0,6 МПа, на сжатие - 7 МПа

Ответ: σ_p= 0,58 МПа < 0,6 МПа; σ_сж = 0,92 МПа < 7 МПа.

Задача 33.

Нормальное напряжение в точке А сжатого бруса (см. рис.) равно 2 МПа (растяжение), в точке В оно равно нулю. Чему равно напряжение в точке С?

Ответ: 6 МПа.

Задача 34.

При сверлении детали на шпиндель А сверлильного станка (см. рисунок) передается осевое давление 15 кН. Определить диаметр круглой чугунной колонны В, если допускаемое напряжение на растяжение равно 35 МПа.

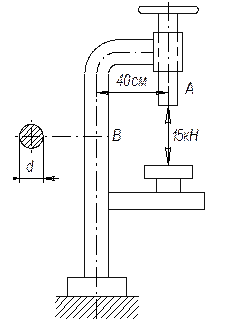
Ответ: 122 мм.

Задача 35.

Нормальное напряжение в точке А сжатого бруса равно 1,2 МПа (растяжение), а в точке В равно нулю. Чему равно напряжение в точке С?

Ответ:

Задача 36.

Колонны круглого и прямоугольного сечений нагружены сжимающими силами в точках А. При этом сжимающие напряжения в этих точках оказались одинаковыми. Сравните напряжения в точках В.

Ответ: .

Задача 37.

В точках А и В колонны приложены одинаковые сжимающие силы. Как изменится наибольшее сжимающее напряжение в колонне, если одну из сил удалить?

Ответ: Не изменится.

Задача 38.

Балка должна передавать на колонну силу F вдоль ее оси. В результате неточности монтажа балка оказалось сдвинутой относительно продольной оси колонны. На сколько процентов увеличилось расчетное нормальное напряжение в колонне по сравнению с проектом?

Ответ: На 30%.

Задача 39.

Стальная полоса растягивается центрально приложенными силами F. Какой глубины а может быть сделана в полосе односторонняя выточка при условии, что наибольшие нормальные напряжения в ней не превысят 150 МПа? Концентрацию напряжений в выточке во внимание не принимать.

Ответ: а=20,7 мм.

Задача 40.

Пружина фрикционной соединительной муфты изготовлена из стальной полосы шириной 40 мм и толщиной 5 мм. При сцеплении двух валов на пружину действуют силы F=2,5 кН. Определить наибольшие сжимающие напряжения, возникающие в сечении mn.

Ответ: .

Задача 41.

Листовой элемент рамы прямоугольного сечения, имеющий внецентренно расположенное сквозное отверстие, нагружен растягивающими силами F=180 кН. Найти наибольшие растягивающие напряжения в ослабленном сечении и построить эпюру напряжений для этого же сечения.

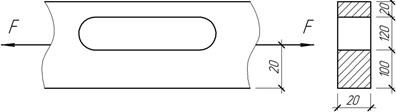
Ответ: .

Задача 42.

Стальной болт М36 (наружный диаметр резьбы 36 мм, внутренний – 30 мм) с костыльной головкой прижимает фланец А к корпусу В с усилием F=20 кН, приложенным с заданным эксцентриситетом е=2,2 см. определить наибольшие растягивающие напряжения в поперечном сечении болта. Во сколько раз изменятся напряжения в болте, если е=0.

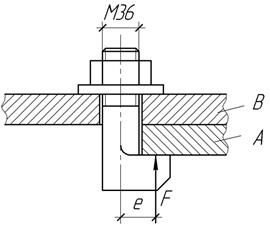
Ответ: , уменьшится в 6,9 раза.

Задача 43.

Стальная струбцина сжимает пакет металлических полос силами F. Какую наибольшую силу F можно принять для струбцины по условию ее прочности, если допускаемое напряжение материала равно [σ]=240 МПа.

Ответ: [F]=10 кН.

Задача 44.

Составить уравнение прямой линии, по которой должна перемещаться продольная сила F, если при этом нулевая линия будет занимать различные положения, вращаясь вокруг точки А.

Ответ:

Задача 45.

Для консольного бруса прямоугольного поперечного сечения определить нормальное напряжение в точке К и построить эпюру нормальных напряжений для заделки.

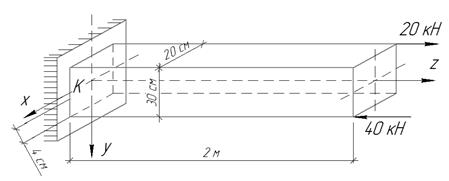
Ответ:

Задача 46.

Короткая чугунная колонна кольцевого поперечного сечения жестко заделана нижним концом. На свободном конце она нагружена продольными сжимающимися силами в точке А F_А=800 кН и в точке В F_В=400 кН. Определить наибольшее сжимающее напряжение и построить эпюру нормальных напряжений для поперечного сечения колонны.

Ответ:

Задача 47.

Определить наибольшее нормальное напряжение и положение нейтральной оси в опасном сечении ломаного стержня, если

Ответ:

Задача 48.

На короткую стойку двутаврового сечения, шарнирно закрепленную по концам, через кронштейн передается нагрузка F=65 кН. Определить необходимый номер двутавра при допускаемом напряжении [σ]=160 МПа.

Ответ: № 22.

Задача 49.

От каких напряжений (растягивающих или сжимающих) произойдет разрушение бетонной колонны, если сжимающая сила будет приложена: а) в точке А? б) в точке В? Зависимость σ от ε считать линейной вплоть до разрушения. Предел прочности при сжатии в 6 раз больше, чем при растяжении.

Ответ: а) сжатие, б) растяжение.

Задача 50.

Найти необходимую толщину полосы, если F=90 кН, [σ]=100 МПа.

Ответ: t=1 см.

Задача 51.

Бетонная дамба высотой Н_д=1,6 м и постоянной толщиной h=0,4 м опирается на прочное основание и служит для удержания воды. Найти максимальное и минимальное напряжения в основании дамбы, когда уровень воды достигнет его верхнего края. При каком максимальном уровне воды в бетоне не возникнут растягивающие напряжения? Принять

Ответ:

Задача 52.

Рама АВС изготовлена из двух стальных труб, сваренных в точке В. Каждая труба имеет площадь поперечного сечения А=100 см², осевой момент инерции I= 8700 см⁴ и наружный диаметр, равный d=30 см. найти наибольшие растягивающие и сжимающие напряжения, возникающие в раме, если F=60 кН, а=2,4 м; Н=1,8 м.

Ответ:

Задача 53.

Столб, служащий для подвески одиночного трамвайного провода состоит из двух швеллеров № 16. Определить напряжения в основании столба, учитывая вес провода G₁=400 Н, вес консоли G₂=600 Н и собственный вес столба G₃.

Ответ:

Задача 54.

Стойка прямоугольного сечения подвергается действию продольной сжимающей силой F. Зная напряжения определить величину силы F и координаты точек ее приложения, а также величину наибольшего сжимающего напряжения.

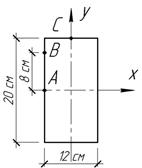
Ответ: F=60 кН,

Задача 55.

Сравнивая наибольшие нормальные напряжения в стойках при действии сжимающей силы F=360 кН.

Ответ:

Задача 56.

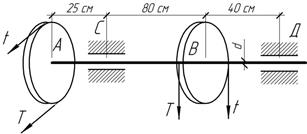
Найти наибольшие напряжения в сечениях 1 – 1 и 2 – 2 стального крюка постоянного круглого сечения диаметром d = 0,032 м, несущего груз F = 8 кН (рис. 1).

Вычислить наибольшее по абсолютной величине напряжение в шарнирно опертой балке прямоугольного поперечного сечения b×h = 0,04×0,06 м с пролетом l = 3 м и загруженной как показано на рис. 2.

При испытании на внецентренное растяжение стального бруса прямоугольного поперечного сечения b×h = 0,005 м×0,06 м поставлены три тензометра Т₁, Т₂, Т₃с одинаковыми коэффициентами увеличения k = 1000 и базой 20 мм (рис. 3). Вычислить какие приращения отсчетов Δ_i должны показать тензометры при ступени нагрузки F = 12 кН, если эксцентриситет сосредоточенной силы F равен е_y = 0,015 м, а модуль упругости материала Е = 2∙10⁵ МПа?

Ответ к рис.1: σ_1-1,_max= 9,95 МПа; σ_2-2,_max= 159 МПа.

Ответ к рис.2: σ= 210,5 МПа.

Ответ к рис.3: ∆₁= 10 мм; ∆₂ = 4 мм; ∆₃ = –2 мм.

Задача 57.

Насколько в процентах увеличится напряжение в короткой стойке квадратного поперечного сечения со стороной а, сжатой центрально приложенной силой F, если в ней сделать врубку, как показано на рис. 1? Насколько изменится напряжение, если сделать две симметричные врубки?

Определить максимально допустимое значение усилия, передаваемого со струбцины (рис.2) на абсолютно жесткое тело К, чтобы деформации в струбцине оставались упругими. Поперечное сечение струбцины прямоугольное b×h = 0,006 м × 0,025 м, размер с = 0,075 м, предел упругости материала струбцины σ_pr= 200 МПа.

Ответ к рис.1: на 70,2%; на 33,3%.

Ответ к рис.2: F_adm = 1,58 кН.

Расчет валов на изгиб с кручением

Задача 1.

Полый стальной вал () подвергается в опасном сечении действию изгибающего момента М_и=90 кНм и крутящего М_к=120 кНм моментов. Используя III гипотезу прочности, определить наружный и внутренний диаметры вала при допускаемом напряжении

Ответ:

Задача 2.

Круглый сплошной вал диаметром 100 мм передает мощность Р=32 кВт при угловой скорости 8 рад/с. Наибольший изгибающий момент равен М_и=3 кНм. Определить расчетные напряжения по III и IV гипотезам прочности.

Ответ:

Задача 3.

Текстолитовая труба с наружным диаметром мм и толщиной t=5 мм подвергается действию крутящего М_к=120 Нм и изгибающего М_и=60 Нм моментов. Определить запас прочности трубки, исходя из IV гипотезы прочности, если предел прочности текстолита .

Ответ:

Задача 4.

Определить диаметр вала круглого сечения, испытывающего действие крутящего момента Т=10 кНм и изгибающего момента М=4 кНм. Если σ_adm=100 МПа. Расчет производить по 3-й теории прочности.

Задача 5.

Керамическая труба подвержена действию крутящего момента Т = 0,08 кНм и изгибающего момента М = 0,06 кНм. Определить запас прочности трубы, если предел прочности материала σ_ut= 100 МПа, наружный диаметр трубы D = 0,05 м, внутренний d = 0,04 м. Расчет вести по критерию удельной потенциальной энергии формоизменения.

У к а з а н и е. Запасом прочности n_В считать отношение предела прочности к расчетному сопротивлению.

Ответ: n_В = 8,7.

Задача 6.

Определить безопасную нагрузку из расчета по III гипотезе прочности, если

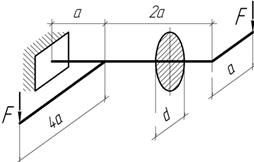
Ответ:

Задача 7.

Стержень АВСD имеет круглое сечение диаметра d. Построить М и Т. Найти взаимный угол поворота и взаимное расхождение торцов в месте приложения нагрузки, если G/Е=0,4. Указание. Использовать при определении перемещений способ Мора-Верещагина.

Задача 8.

Проверить прочность круглого стержня диаметром d=20 мм, пользуясь III гипотезой прочности, если F=1 кН, М=42,7 Нм, .

Ответ:

Задача 9.

Дорожный знак укреплен на круглой трубчатой стойке с наружным диаметром d=80 мм. Используя третью гипотезу прочности, определить необходимую толщину стенки стойки при допускаемом напряжении [σ]=80 МПа, если наибольшая ветровая нагрузка на знак равна Р=1,5 кПа.

Ответ: t=2,4 мм.

Задача 10.

Кронштейн выполнен из круглого стержня диаметром d=70 мм. Найти наибольшее эквивалентное напряжение по III гипотезы прочности, если F=4 кН, а=0,5 м.

Ответ:

Задача 11.

Определить размеры поперечного сечения ломанного стержня из расчета по III гипотезе прочности, если

Ответ: d=60 мм.

Задача 12.

Определить наибольшее расчетное напряжение в стольном стержне круглого сечения, нагруженном двумя одинаковыми силами F=1 кН. Чему будет равно это напряжение, если одну из сил убрать? Использовать IV гипотезу прочности.

Задача 13.

Какой вариант нагружения (а или б) наиболее благоприятен с точки зрения прочности стержня?

Задача 14.

Какое из нагружений круглого стержня, выполненного из пластического материала, наиболее опасно?

Задача 15.

Стержень квадратного сечения bxb нагружен тремя одинаковыми моментами М_х=М_у=М_z=М. В какой точке возникают наибольшие напряжения?

Задача 16.

Вал диаметром 70 мм несет шкив ременной передачи весом G=5 кН. Определить расчетное напряжение в вале по III гипотезе прочности, если натяжения ветвей равны Т=10 кН и t=5 кН, а диаметр шкива равен D=80 см.

Ответ:

Задача 17.

В зацепление на зубчатое колесо действует окружная сила F_х=2,5 кН и радиальная F_у=0,8 кН. Определить диаметр вала по III гипотезе прочности, если [σ]=80 МПа, D=40 см.

Ответ: d=45 мм.

Задача 18.

Промежуточный вал редуктора передает мощность Р=10 кВт при угловой скорости ω=10 рад/с. Определить диаметр вала по III гипотезе прочности, если F₁=4 кН, F₂=2 кН, [σ]=80 МПа, а=0,2 м.

Ответ: d=55 мм.

Задача 19.

Вал передает мощность Р=7 кВт при угловой скорости ω=10 рад/с. Обе ветви ремня на шкиве А горизонтальны, а на шкиве В вертикальны. Исходя из III гипотезы прочности, определить необходимый диаметр вала, если t=1,5 кН, [σ]=80 МПа, диаметры шкивов одинаковы и равны D=60 см.

Ответ: d=60 мм.

Задача 20.

Дюралюминиевая трубка с наружным диаметром 80 мм и толщиной стенки 5 мм скручивается равномерно распределенными по ее длине моментами интенсивностью m=300 кН/м и изгибается равномерно распределенной поперечной нагрузкой интенсивностью q=200 Н/м. Определить в опасном сечении трубки расчетное напряжение по III гипотезе прочности, а также найти наибольший прогиб и угол закручивания трубки, если Е=70ГПа, G=27 ГПа.

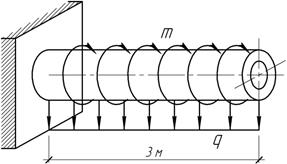
Ответ:

Задача 21.

Оба конца стального стержня АВ квадратного сечения 2х2 см жестко защемлены. посредине пролета l=160 см к нему жестко прикреплена стальная поперечина СД такого же сечения, длиной а=30 см; на свободном конце ее приложена сила F=300 Н. Определить расчетные напряжения в стержнях по III гипотезе прочности и найти перемещение точки Д в направлении силы F.

Ответ:

Задача 22.

Кронштейн выполнен из круглого стержня диаметром d=70 мм. Найти наибольшее эквивалентное напряжение по III гипотезе прочности, если F=4 кН, а=0,5 м.

Ответ: =133 МПа.

Задача 23.

Полукольцо круглого очертания, жестко заделанное одним концом, нагружено сосредоточенной силой F на свободном конце. Вычислить наибольшее значение допускаемой силы F, исходя из IV гипотезы прочности, если [σ]=120 МПа.

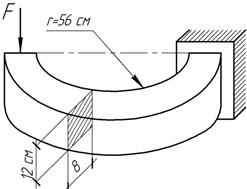
Ответ: [F]=10,2 кН

Задача 24.

Определить размеры поперечного сечения ломаного стержня из расчета по III гипотезе прочности, если [σ]=160 МПа.

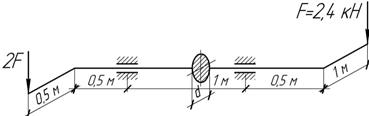
Ответ: d=60 мм.

Задача 25.

Определить безопасную нагрузку из расчета по третьей гипотезе прочности, если [σ]=160 МПа, а=39 см, d=10 см.

Ответ: [F]=8 кН.

Задача 26.

Определить размеры поперечного сечения стержня из расчета по III гипотезе прочности, если F=10 кН, [σ]=180 МПа.

Ответ: а=10 см.

Задача 27.

Проверить прочность круглого стержня диаметром d=20 мм, пользуясь III гипотезой прочности, если F=1 кН, М=42,7 Нм, [σ]=160 МПа.

Ответ:

Задача 28.

Стальной коленчатый стержень АВСД, имеющий на участке АВ круглое сечение диаметром 125 мм, нагружен в точке К силой F=20 кН, перпендикулярной к плоскости чертежа. Пренебрегая касательными напряжениями от поперечной силы, определить в наиболее опасной точке сечения mn главные напряжения и эквивалентные напряжения по третьей и четвертой гипотезам прочности.

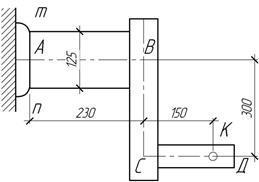
Ответ:

Задача 29.

К рукоятке подъемной лебедки приложены две сосредоточенные силы по 200 Н каждая. Определить наибольшее расчетное напряжение по четвертой гипотезе прочности, возникающее в поперечном сечении кривошипа АВ. Расчетное значение кривошипа принять на расстоянии 40 см от оси рукоятки.

Ответ:

Задача 30.

Посредине стального вала насажен шкив ременной передачи весом G=4 кН. Натяжение горизонтально расположенных ветвей ремня равны T=4 кН и t=2 кН. Вал вращается с угловой скоростью ω=16,7 рад/с и передает мощность 14,7 кВт. Определить диаметр вала, используя третью гипотезу прочности, если l=2 м, [σ]=60 МПа.

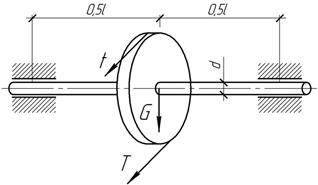
Ответ: d=86 мм.

Задача 31.

Определить размеры поперечного сечения ломаного стержня из расчета по третьей гипотезе прочности, если F=4,2 кН, [σ]=150 МПа, а=30 см.

Ответ: d=50 см.

Задача 32.

Из условия прочности по гипотезе наибольших касательных напряжений определить наибольшую допускаемую величину груза G, которую можно поднять при помощи ворота. Вал ворота круглого поперечного сечения диаметром d=30 мм. Допускаемое напряжение для материала вала [σ]=80 МПа.

Ответ: [G]=790 Н.

Задача 33.

Ответ: t=2,4 мм.

Задача 34.

Круглый дорожный знак укреплен на полой круглой стойке с наружным диаметром 6 см (см. рисунок). Исходя из условия прочности по теории касательных напряжений, определить толщину стенки стойки при допускаемом напряжении [σ] = 60 МПа, если наибольшая ветровая нагрузка на знак равна 20 МПа.

Ответ: 0,265 см.

Задача 35.

Исходя из условия прочности по теории касательных напряжений, определить наибольшую допускаемую величину груза F, который можно поднять при' помощи ворота (см. рисунок). Вал ворота круглого поперечного сечения диаметром 30 мм. Допускаемое напряжение для материала вала равно 80 МПа.

Ответ: 790 Н.

Задача 36.

Два одинаковых шкива А и В насажены на вал (см. рисунок). Ведущий шкив А передает 10 л. с. при 100 об/мин. Обе ветви ремня на шкиве А горизонтальны, на шкиве В - вертикальны. Натяжение ремня F₂ =1500 H. Диаметры шкивов равны 60 см. Весами шкивов можно пренебречь. Исходя из условия прочности по теории касательных напряжений, определить необходимый диаметр вала при допускаемом напряжении [σ] = 80 МПа.

Ответ: 59,6 мм ≈ 60 мм.

Задача 37.

Схема нагружения вала рулевой машины представлена на рисунке. Требуется подобрать диаметр вала, используя критерий наибольших касательных напряжений (d_I ) и критерий удельной потенциальной энергии формоизменения (d_II), и считая R_adm = 30 МПа.

Ответ: d_I =0,266 см; d_II =0,26 см.

Задача 38.

Вал со шкивами диаметрами D₁ = 0,4 м и D₂ = 0,6 м (см. рис.) вращается со скоростью n₀ = 100 об/мин и передает мощность U = 30 кВт. Собственный вес левого шкива G₁= 2 кН, правого шкива G₂= 3 кН, собственным весом вала пренебречь. Ремни левого шкива направлены вертикально, правого – горизонтально. У обоих шкивов натяжение в ведущем ремне вдвое больше, чем в ведомом. Рассчитать диаметр вала (единый по длине), используя критерий наибольших касательных напряжений (d_I) и критерий удельной потенциальной энергии формоизменения (d_II), и считая R_adm = 80 МПа.

У к а з а н и е. Для расчета скручивающего момента М_к нужно воспользоваться формулой

(U в кВт),

Ответ: d_I = 10,5 см; d_II = 10,4 см.

Задача 39.

Стержень с ломаной осью и диаметром D = 0,1 м одним концом защемлен, а на другом нагружен силой F = 5 кН. Размеры участков стержня указаны на рис.1. Найти эквивалентное напряжение, используя критерий удельной потенциальной энергии формоизменения.

Пользуясь критерием наибольших касательных напряжений, подобрать диаметр стального вала лебедки (рис.2) грузоподъемностью F = 40 кН при невыгоднейшем положении груза. Диаметр посаженного на вал барабана D = 0,4 м. Расстояние между осями подшипников вала равно 1 м. Допускаемое напряжение R_adm = 100 МПа.

Ответ к рис.1: σ_экв= 109 МПа.

Ответ к рис.2: d= 10,9 см.

Задача 40.

Подобрать диаметры вала на участках АВ и СD для коленчатого вала, нагруженного так, как показано на рисунке. Использовать критерий наибольших касательных напряжений (d_I) и критерий удельной потенциальной энергии формоизменения (d_II), считая R_adm =80 МПа. Принять F = 2 кН, а = 0,1 м.

Ответ: d_I = 3,08 см; d_II = 3,04 см.

Общий случай сложного сопротивления

Задача 1.

Грузовой винт домкрата имеет внутренний диаметр резьбы Грузоподъемность домкрата F=100 кН. На винт действует крутящий момент от трения в резьбе М_к=580 Нм. Определить по III гипотезе прочности величину наибольшего эквивалентного напряжения.

Ответ:

Задача 2.

Винт струбцинки для сжатия деталей испытывает действие сжимающей силы F=18 кН и крутящего момента М_к=200 Нм. Определить внутренний диаметр винта, исходя из III гипотезы прочности, если [σ]=80 МПа.

Ответ:

Задача 3.

Пользуясь IV гипотезой прочности, проверить прочность стержня АВ кольцевого сечения, если F₁=250 кН, F₂30 кН, [σ]=160 МПа.

Ответ:

Задача 4.

В опасном сечении вала действуют указанные на рисунке внутренние силовые факторы. Определить диаметр вала по III гипотезе прочности и указать положение опасной точки, если допускаемое напряжение [σ]=120 МПа.

Ответ: d=58 мм, х=1,42 см; у=-2,53 см.

Задача 5.

Тонкостенная стальная трубка с наружным диаметром d=10 мм и толщиной стенки t=0,5 мм нагружена одновременно внутренним гидростатическим давлением р=15 МПа, продольной растягивающей силой F=1 кН и крутящим моментом М_к=3 Нм. Определить расчетное напряжение в трубке, пользуясь III гипотезой прочности.

Ответ:

Задача 6.

На консольную часть трубчатого вала редуктора насажена коническая шестерня, на которую действуют три силы: F_х=1,8 кН, F_у=0,6 кН, F_z=0,3 кН. Определить наружный диаметр вала, исходя из III гипотезы прочности, если [σ]=100 МПа,

Ответ: d=27 мм.

Задача 7.

Цилиндрический баллон подвергается одновременному действию внутреннего давления р=6 МПа, изгибающего момента М_и=2 кНм и крутящего момента М_к=5 кНм. Проверить прочность баллона по IV гипотезе прочности, если наружный диаметр d=10 см, толщина стенки t=0,5 см, [σ]=160 МПа.

Ответ:

Онлайн-калькулятор "Напряжения при косом изгибе прямоугольного сечения"

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00