Главная
Лекция 3.
Теория сложного напряженно-деформированного состояния
(НДС) твердого тела
Содержание
Напряжённое и деформированное
состояние частицы тела
Основные виды
напряжённо-деформированного состояния (НДС)
Общий случай НДС. Обобщённый закон
Гука-Коши
Определение напряжений на
произвольно ориентированной площадке
Главные оси и главные напряжения в плоских
задачах
Главные деформации в плоских задачах
Главные нормальные напряжения
и направления в общем случае объёмного напряжённого состояния
Обзор различных типов напряженных
состояний
Общее решение кубического уравнения для определения главных напряжений
Напряжения на октаэдрических площадках
Определение удлинений и сдвигов для
произвольно направленных волокон
Общее решение кубического
уравнения для определения главных деформаций
Дифференциальные
уравнения равновесия Коши
Уравнение совместности
деформаций
Кручение призматических
стержней произвольного поперечного сечения
Кручение стержня
эллиптического сечения
Кручение стержня
прямоугольного сечения
Кручение стержня треугольного
сечения
Напряжённое и деформированное состояние частицы тела
Теория НДС ставит своей задачей определение внутренних напряжений, деформаций и перемещений в различных точках деформируемого твёрдого тела произвольной формы и размеров.
В нагруженном
какой-то нагрузкой теле в каждой точке сеченияв общем
случае возникают нормальное напряжение ![]() ,
направленное перпендикулярно к сечению, и касательное
,
направленное перпендикулярно к сечению, и касательное ![]() ,
лежащее в плоскости сечения. Как известно, через точку можно провести
бесконечное количество плоскостей и в этой точке будут напряжения
,
лежащее в плоскости сечения. Как известно, через точку можно провести
бесконечное количество плоскостей и в этой точке будут напряжения ![]() и
и ![]() ,
перпендикулярные и лежащие в этих плоскостях. Таким образом, напряженное
состояние в точке можно представить совокупностью всех
,
перпендикулярные и лежащие в этих плоскостях. Таким образом, напряженное
состояние в точке можно представить совокупностью всех ![]() и
и ![]() ,
возникающих в ней. Для характеристики напряженного состояния в точке достаточно
знать значения нормальных и касательных напряжений на трех взаимно
перпендикулярных площадках (будет доказано позднее). Их удобнее представить в
виде параллелепипеда с бесконечно малыми гранями. Поскольку расстояние между
гранями бесконечно мало, то можно считать, что на противоположных гранях параллелепипеда
возникают одинаковые по величине напряжения, но направленные противоположно.
,
возникающих в ней. Для характеристики напряженного состояния в точке достаточно
знать значения нормальных и касательных напряжений на трех взаимно
перпендикулярных площадках (будет доказано позднее). Их удобнее представить в
виде параллелепипеда с бесконечно малыми гранями. Поскольку расстояние между
гранями бесконечно мало, то можно считать, что на противоположных гранях параллелепипеда
возникают одинаковые по величине напряжения, но направленные противоположно.
Напряженным
состоянием тела в точке называют
совокупность нормальных и касательных напряжений, действующих по трем взаимно
перпендикулярным площадкам (сечениям), содержащим данную точку.
Отнесём тело к координатным осям x, y, z и выделим мысленно из него материальную частицу в виде параллелепипеда или кубика размерами dx, dy, dz (рис. 3.1).
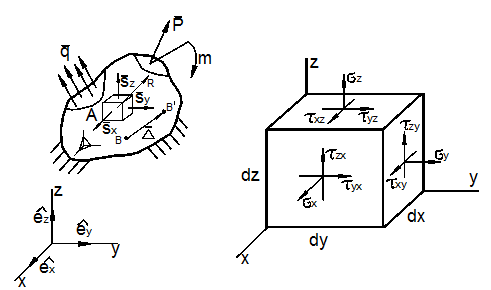
а)
б)
Рис. 3.1
Действия отброшенной
части тела заменим векторами – напряжениями ![]() и разложим их на составляющие по координатным
осям.
и разложим их на составляющие по координатным
осям.

где ex, ey, ez -
единичные векторы, направленные вдоль координатных осей x, y, z; ![]() -
нормальные напряжения,
-
нормальные напряжения, ![]() -
касательные напряжения. У касательных напряжений первый индекс указывает на
направление его действия, второй индекс – на нормаль к площадке, на которой оно
действует. Например,
-
касательные напряжения. У касательных напряжений первый индекс указывает на
направление его действия, второй индекс – на нормаль к площадке, на которой оно
действует. Например, ![]() — это касательное напряжение, действующее на
площадке, перпендикулярной оси Х и
направленное вдоль оси У. У нормальных напряжений индекс соответствует
одновременно как направлению, так и нормали к площадке их действия. На невидимых на рис. 3.1 гранях частицы действуют такие же, но
противоположно направленные напряжения.
— это касательное напряжение, действующее на
площадке, перпендикулярной оси Х и
направленное вдоль оси У. У нормальных напряжений индекс соответствует
одновременно как направлению, так и нормали к площадке их действия. На невидимых на рис. 3.1 гранях частицы действуют такие же, но
противоположно направленные напряжения.
Совокупность указанных напряжений полностью характеризует напряжённое состояние частицы тела. Эту совокупность записывают в виде квадратной матрицы
![]()
и называют тензором напряжений Коши. Система напряжений, приложенных к частице тела, должна удовлетворять условиям равновесия. Первые три условия в проекциях на оси x, y, z дают тождества, т.к. на противоположных гранях мы считаем напряжения равными по величине. Остаётся проверить, обращаются ли в нуль суммы моментов всех сил относительно координатных осей. Составим условие равновесия моментов относительно оси х:
![]()
откуда следует
![]() . Аналогично можно составить два
уравнения равновесия моментов относительно осей y и z. В
результате получим соотношения:
. Аналогично можно составить два
уравнения равновесия моментов относительно осей y и z. В
результате получим соотношения:
![]()
которые
называют законом парности касательных
напряжений: на двух взаимно перепендикулярных площадках составляющие касательных
напряжений, ортогональные их общему ребру, равны по величине и направлены оба
либо к ребру, либо от него. На основании этого закона тензор-матрица
напряжений ![]() является симметричной относительно главной
диагонали, состоящей из нормальных напряжений.
является симметричной относительно главной
диагонали, состоящей из нормальных напряжений.
Напряжение
![]()
называют средним
напряжением. Тензор напряжений, для которого ![]() ,
называется тензором–девиатором напряжений.
,
называется тензором–девиатором напряжений.
Напряженное состояние в точке можно представить как сумму состояний:
напряженное состояние, в котором все три главные
напряжения равны ![]() (всестороннее
растяжение или сжатие) и напряженное состояние, на гранях которого нормальные
напряжения представляют собой разность
(всестороннее
растяжение или сжатие) и напряженное состояние, на гранях которого нормальные
напряжения представляют собой разность ![]() и
и ![]() .
.
В общем случае тензор напряжений можно разложить на сумму двух тензоров:
![]()
Первый из них
![]()
носит название шарового тензора напряжений, а второй:
![]()
тензора–девиатора или просто девиатора
напряжений.
Иногда компоненты девиатора напряжений обозначают:

Шаровой тензор характеризует напряженное состояние всестороннего растяжения – сжатия частицы тела, а девиатор – напряженное состояние её формоизменения.
На каждую частицу тела кроме напряжений действуют объёмные силы:
![]()
где Rx, Ry, Rz – проекции этих сил на координатные оси. Каждая вектор-сила ![]() действует на единицу объёма.
действует на единицу объёма.
На поверхности тела F на каждую единицу её площади могут действовать распределённые силы:
![]()
где qx, qy, qz – проекции этих сил.
Если последние
действуют на малых площадках контакта ![]() поверхности
тела, то их, согласно принципу смягчения граничных условий Сен-Венана, заменяют
главными вектором
поверхности
тела, то их, согласно принципу смягчения граничных условий Сен-Венана, заменяют
главными вектором ![]() и моментом
и моментом ![]() всех сил, действующих на этих малых площадках:
всех сил, действующих на этих малых площадках:
![]()
где ![]() - радиус – вектор, проведённый из заданной
точки (центра приведения сил) на
- радиус – вектор, проведённый из заданной
точки (центра приведения сил) на ![]() до текущей силы
до текущей силы ![]() .
.
В результате
действия на тело внешних сил ![]() температуры Т каждая точка В совершает перемещение
температуры Т каждая точка В совершает перемещение ![]() в новое положение В’. Это перемещение характеризуется направленным отрезком
в новое положение В’. Это перемещение характеризуется направленным отрезком ![]() ,
т.е. вектором перемещения:
,
т.е. вектором перемещения:
![]()
где u, v, w – проекции этого перемещения на координатные оси.
Перемещения ![]() характеризуют деформацию тела в целом.
Например, прогибы точек оси балки V и поворот поперечных сечений,
проходящих через эти же точки, характеризуют деформацию балки в целом при её изгибе.
характеризуют деформацию тела в целом.
Например, прогибы точек оси балки V и поворот поперечных сечений,
проходящих через эти же точки, характеризуют деформацию балки в целом при её изгибе.
Деформация
тела складывается из деформации её материальных (физических) частиц, каждая из
которых испытывает удлинения ![]() в направлении её рёбер и искажения прямых
углов:
в направлении её рёбер и искажения прямых
углов:
![]()
между её гранями в каждой из координатных плоскостей (рис. 3.2).
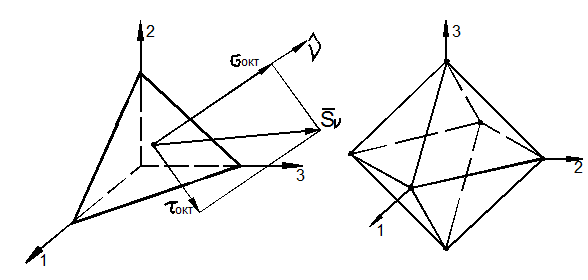
Величины
![]()
называют относительными удлинениями или деформациями частиц тела. Половины сдвигов обозначают:
![]()
Совокупность шести компонентов деформации полностью характеризует деформированное состояние частицы тела. Эту совокупность запишем в виде квадратной матрицы:
![]()
и назовем тензором деформаций Коши.

а)
б)
Рис. 3.2
Величину
![]()
называют средней деформацией.
Если для
рассматриваемого тензора деформация ![]() ,
то он называется тензором-девиатором или просто девиатором
деформации.
,
то он называется тензором-девиатором или просто девиатором
деформации.
В общем случае
![]() тензор (7) можно разложить на сумму двух
тензоров:
тензор (7) можно разложить на сумму двух
тензоров:
![]()
Первый из них:
![]()
носит название шарового тензора деформации и описывает объёмную деформацию всестороннего растяжения – сжатия.
Второй тензор:
![]()
представляет собой тензор-девиатор и характеризует деформацию изменения формы частиц тела.
Основные виды напряжённо-деформированного состояния (НДС)
До сих пор мы рассматривли в основном простейшие виды НДС – растяжение – сжатие, плоский чистый сдвиг и их комбинацию (рис. 3.3).

а)
б)
в)
Рис. 3.3
Они
встречаются при растяжении и сжатии стержня и его кручении, а также при изгибе
(рис. 3.4). При растяжении и сжатии (рис. 3.4,а) осевая ![]() и поперечные деформации
и поперечные деформации ![]() определяются законами Гука и Пуассона:
определяются законами Гука и Пуассона:
![]()
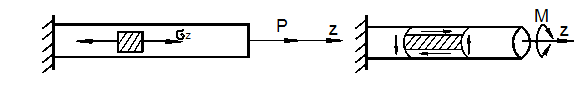
а) Растяжение
б) Кручение

в) Изгиб
Рис. 3.4
При плоском чистом сдвиге (рис. 3.4,б) деформация сдвига
![]()
Часто на практике встречаются двухосное растяжение и его комбинация с чистым сдвигом (рис. 3.5).

а)
б)
Рис. 3.5
В последнем случае состояние называют плоским напряжённым состоянием. Оно возникает в тонкостенных элементах конструкций, таких как плиты (пластины) и оболочки (рис. 3.6).
При двухосном
растяжении деформации в направлениях x и y
могут быть найдены на основании законов (11) для одноосного растяжения.
Представим ![]() на основании принципа независимости действия
сил (напряжений
на основании принципа независимости действия
сил (напряжений ![]() )
в виде суммы деформаций в каждом из направлений x и y от этих сил:
)
в виде суммы деформаций в каждом из направлений x и y от этих сил:


а)
б)
Рис. 3.6
Для плоского напряжённого состояния (рис. 3.6,б) с учётом (12) получаем:
При трёхосном растяжении (рис. 3.7,а) на основании законов (11) аналогичным образом получаем:

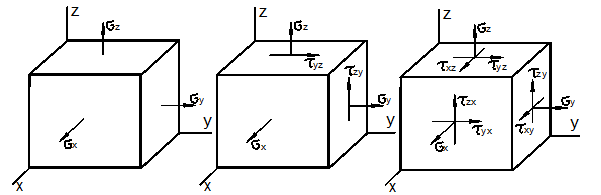
а) Трёхосное б)
Плоская в) Объёмное
напряжённое
растяжение
деформация
состояние
Рис. 3.7
Если сложить соотношения (15), то получим закон упругого изменения объёма:
![]()
где ![]() – относительное изменение объёма, (17)
– относительное изменение объёма, (17)
![]() –
модуль объёмной деформации.
(18)
–
модуль объёмной деформации.
(18)
На практике часто встречается напряжённое состояние, изображённое на рис. 3.7,б. Оно возникает в удлинённых телах со стеснённой в этих направлениях деформацией. Примером могут служить подпорная стенка, тело плотины, железнодорожный рельс и др. В этих случаях призматическое тело как бы зажато между двумя опорами, а нагрузка вдоль тела остаётся неизменной (рис. 3.8).

а)
б)
в) г)
Рис. 3.8
Произвольная
точка А тела
при деформации остаётся лежать в одной плоскости, параллельной плоскости x, y. Напряжённое состояние отличается от
плоского тем, что возникает напряжение ![]() .
Соответствующее деформированное состояние тела носит название плоской
деформации. Относительные деформации определяются соотношениями закона
Гука, полученные использованием принципа независимости действия сил (напряжений).
Накладывая на соотношения (5) при трёхосном растяжении плоский чистый сдвиг с
напряжениями
.
Соответствующее деформированное состояние тела носит название плоской
деформации. Относительные деформации определяются соотношениями закона
Гука, полученные использованием принципа независимости действия сил (напряжений).
Накладывая на соотношения (5) при трёхосном растяжении плоский чистый сдвиг с
напряжениями ![]() ,
получаем:
,
получаем:

Характерным примером возникновения объёмной НДС могут служить контактные задачи. Например, задачи о контакте колёс вагона с рельсами, задача о вдавливании шарика в подшипнике, шаровой опоры в фундамент и др. (рис. 3.9,а).
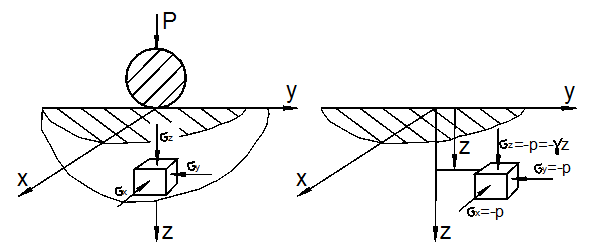
а) б)
Рис. 3.9
Кубик, опущенный в воду (рис. 3.9,б), будет испытывать всестороннее сжатие напряжениями
![]()
![]()
где ![]() - удельный вес воды.
- удельный вес воды.
Другим близким
примером могут служить полупространства, представляющие собой модель грунтовой
среды. Слой грунта толщины z
оказывает на нижележащие слои давление ![]() ,
где
,
где ![]() -
удельный вес грунта. Напряжения
-
удельный вес грунта. Напряжения ![]() .
Деформации
.
Деформации ![]() , и согласно (12):
, и согласно (12):
![]()
откуда
![]()
где
![]()
называется коэффициентом
бокового давления среды. Если ![]() =0,5,
то
=0,5,
то ![]() и частица будет испытывать всестороннее сжатие,
т.к.:
и частица будет испытывать всестороннее сжатие,
т.к.:
![]()
При этом
изменение объёма ![]() так как
так как ![]() .
Такая среда называется несжимаемой.
.
Такая среда называется несжимаемой.
Общий случай НДС. Обобщённый закон Гука-Коши
Рассмотрим далее общий случай объёмного напряжённо-деформированного состояния (рис. 3.10).

Рис. 3.10
Его можно
разложить на сумму двух состояний – трёхосное растяжение и сложный сдвиг в трёх
координатных плоскостях. На основании принципа независимости действия сил
(напряжений), используя (19) и ![]() ,
получаем:
,
получаем:
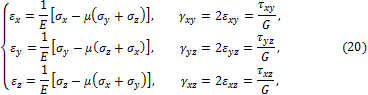
Уравнения (20) можно разрешить относительно напряжений:

где
![]()
Коэффициент ![]() называют модулем Коши – Ламе.
называют модулем Коши – Ламе.
Из (20), (21) следует ещё одна форма записи обобщённого закона Коши – Гука в форме трёх законов:
1. Закон упругого изменения объёма
Складывая в (20) относительные удлинения, получаем:
![]()
где ![]() -
относительное изменение объёма,
-
относительное изменение объёма, ![]() -
модуль деформации.
-
модуль деформации.
2. Закон упругого формоизменения
Составим на основании (20), (23) выражение:
![]()
Аналогично
можно найти разности ![]() .
В результате получаем соотношения
.
В результате получаем соотношения

представляющие закон упругого формоизменения. Соотношения (24) связывают компоненты девиаторов напряжений и деформаций.
3. Закон
упругого упрочнения материала
Величину
![]()
называют модулем
девиатором напряжений.
Из (24) следует:

Подставляя полученные выражения в (25), находим:
![]()
где величина
![]()
носит название
модуля-девиатора
деформаций. Соотношение
(26) выражает собой закон упругого упрочнения материала. В частном случае
простого растяжения ![]() и соотношение (26) принимает вид
и соотношение (26) принимает вид
![]()
Таким образом,
закон упругого упрочнения (26) с точностью до постоянного множителя ![]() совпадает графически с упругим участком
диаграммы растяжения.
совпадает графически с упругим участком
диаграммы растяжения.
Определение напряжений на произвольно ориентированной площадке
Рассечём частицу тела около произвольной точки А (рис. 3.11) наклонной плоскостью, направление единичной нормали
![]()
к которой определено направляющими косинусами ![]() (рис. 3.11,а).
В результате мы получили фигуру четырёхугольник, или тетраэдр. При уменьшении расстояния AN = h до нуля наклонная плоскость пройдёт через
точку А. Обозначим площадь
наклонной грани через dF, а площади
координатных граней
(рис. 3.11,а).
В результате мы получили фигуру четырёхугольник, или тетраэдр. При уменьшении расстояния AN = h до нуля наклонная плоскость пройдёт через
точку А. Обозначим площадь
наклонной грани через dF, а площади
координатных граней ![]() .
Вектор
.
Вектор ![]() на произвольно ориентированной площадке с
нормалью v и площадью dF
разложим на составляющие:
на произвольно ориентированной площадке с
нормалью v и площадью dF
разложим на составляющие:
![]()
где ![]() - проекции напряжения на координатные оси.
- проекции напряжения на координатные оси.
Проецируя все силы, действующие на тетраэдр, последовательно на оси x, y, z и сокращая на dF, получим:
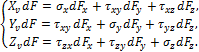

а)
б)
Рис. 3.11
Очевидно, что площади координатных граней:
![]()
Поэтому после сокращения на dF, получаем формулы

называемые формулами
Коши.
Таким образом,
проекции вектора напряжений ![]() на произвольно ориентированной площадке с
направляющими косинусами
на произвольно ориентированной площадке с
направляющими косинусами ![]() выражается через шесть компонент напряжённого
состояния, совокупность которых образует тензор напряжений. При помощи формул Коши
(29) можно найти величину полного напряжения:
выражается через шесть компонент напряжённого
состояния, совокупность которых образует тензор напряжений. При помощи формул Коши
(29) можно найти величину полного напряжения:
![]()
Вектор
напряжений ![]() может быть разложен также на нормальную
может быть разложен также на нормальную ![]() и касательную
и касательную ![]() составляющие:
составляющие:
![]()
где t – единичный вектор касательной. Тогда
![]()
Выразим
нормальное напряжение ![]() через проекции
через проекции ![]() вектора
вектора ![]() :
:
![]()
и заменим эти проекции согласно (29). Получим формулу:
![]()
Если единичный
касательный вектор
![]()
то
![]()
где ![]() направляющие
косинусы вектора t,
определяющие направление действия касательного напряжения
направляющие
косинусы вектора t,
определяющие направление действия касательного напряжения ![]() .
.
Подставляя в
(33) вместо ![]() их выражения (29), получаем:
их выражения (29), получаем:
![]()
В частном случае плоской задачи имеем (рис. 3.12):
![]()
Из (32), (34) находим:

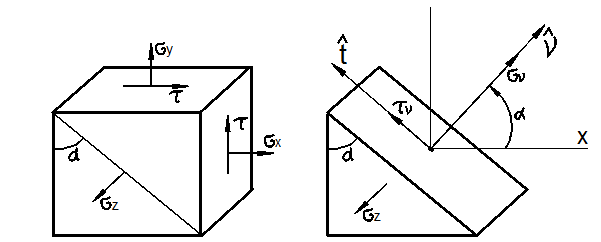
Рис. 3.12
где использованы соотношения
![]()
Главные оси и главные напряжения в плоских задачах
Рассмотрим напряжённое состояние, характеризуемое тензором напряжений:

Если ![]() ,
то напряжённое состояние называется плоским. Если
,
то напряжённое состояние называется плоским. Если ![]() ,
то напряжённое состояние соответствует плоской деформации. Найдём
экстремальные значения нормального напряжения
,
то напряжённое состояние соответствует плоской деформации. Найдём
экстремальные значения нормального напряжения ![]() для плоских задач.
для плоских задач.
Дифференцируя
выражение (35) для ![]() по
по ![]() , и приравниваем полученный результат к
нулю:
, и приравниваем полученный результат к
нулю:
![]()
откуда получаем:
![]()
Из (36)
находим два значения угла ![]() и
и ![]() (рис. 3.13), определяющие два направления и
две площадки, называемые главными.
(рис. 3.13), определяющие два направления и
две площадки, называемые главными.

Рис. 3.13
Экстремальные
значения напряжений ![]() и
и ![]() называются главными нормальными
напряжениями. На главных площадках касательные напряжения отсутствуют.
Поэтому третья площадка, на которой действует нормальное напряжение
называются главными нормальными
напряжениями. На главных площадках касательные напряжения отсутствуют.
Поэтому третья площадка, на которой действует нормальное напряжение ![]() ,
будет также главной. Главным будет напряжение
,
будет также главной. Главным будет напряжение ![]() .
.
Так как
![]()
то, с учётом (36) из (35), получаем значения главных нормальных напряжений:
![]()
Обычно принято
главные напряжения нумеровать так, чтобы ![]()
В частном
случае чистого сдвига ![]() (рис. 3.14).
(рис. 3.14).

Рис. 3.14
Из (37)
получаем: ![]()
В случае
растяжения напряжениями ![]() и чистого сдвига напряжениями
и чистого сдвига напряжениями ![]() имеем:
имеем:
![]()
Если частица отнесена к главным осям (рис. 3.15), то формулы (35) принимают вид

Из (38) видно,
что максимальное касательное напряжение по модулю возникает при ![]() т.е. на площадках, наклонённых к главным
осям под углом
т.е. на площадках, наклонённых к главным
осям под углом ![]() .
В этом случае
.
В этом случае
![]()
![]()
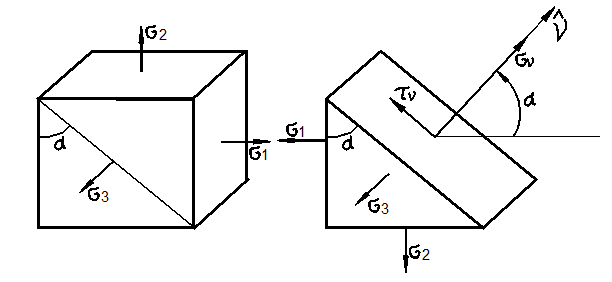
Рис. 3.15
Как видно из
(39), на площадке, где действует ![]() ,
нормальное напряжение
,
нормальное напряжение ![]() отлично от нуля и равно полусумме нормальных
напряжений
отлично от нуля и равно полусумме нормальных
напряжений ![]() .
.
Главные деформации в плоских задачах
Рассмотрим
частицу тела с напряжениями ![]() (рис. 3.16,а).
Повернём её на угол
(рис. 3.16,а).
Повернём её на угол ![]() относительно оси z. На гранях такой частицы действуют
напряжения
относительно оси z. На гранях такой частицы действуют
напряжения ![]() (рис. 3.16,б).
(рис. 3.16,б).
Предположим,
что имеет место плоское напряжённое состояние ![]() Тогда, на основании (35), получаем:
Тогда, на основании (35), получаем:

Рис. 3.16
Заметим, что
направление касательного вектора ![]() отличается от
отличается от ![]() на 900 и поэтому при вычислении
на 900 и поэтому при вычислении ![]() угол
угол ![]() следует заменить на
следует заменить на ![]() .
.
Найдём деформации повёрнутой частицы, используя закон Гука для плоских задач:

Из (40), (41) получаем:
![]()

Формулы (42) аналогичны (35). Найдём теперь экстремальные (главные) значения деформации. Из условия экстремума:
![]()
получаем
![]()
Используя выражение (43) находим главные значения деформаций:
![]()
Как видно, при
использовании закона Гука главные направления тензоров напряжений и деформаций
совпадают. Это предположение было сделано Коши. Если ![]() 0 (плоская деформация,
0 (плоская деформация, ![]() ),
то формулы для главных деформаций
),
то формулы для главных деформаций ![]() не изменяется.
не изменяется.
Главные нормальные напряжения и направления в общем случае объёмного напряжённого состояния
Плоские задачи
являются частным случаем объёмного напряжённого состояния. Поставим задачу по
определению таких площадок, на которых действуют только экстремальные
нормальные напряжения, а касательные обращаются в нуль (рис. 3.17). Такие
площадки назовём главными, а соответствующие экстремальные значения нормальных
напряжений – главными нормальными напряжениями. Будем обозначать их ![]() и считать, что
и считать, что ![]() .
.
Направляющие
косинусы нормали ![]() на площадке общего положения удовлетворяют
условию
на площадке общего положения удовлетворяют
условию
![]()
Следовательно,
возникает задача об отыскании условного экстремума напряжения ![]() при дополнительном условии (45).
при дополнительном условии (45).

Рис. 3.17
Составим функцию Лагранжа:
![]()
где ![]() играет роль неопределённых множителей
Лагранжа. Найдём безусловный экстремум функции F по переменным
играет роль неопределённых множителей
Лагранжа. Найдём безусловный экстремум функции F по переменным ![]() .
Для этого найдём частные производные по этим переменным и приравняем их к нулю:
.
Для этого найдём частные производные по этим переменным и приравняем их к нулю:

![]()
Так как ![]() одновременно обратиться в нуль не могут, то
система трёх однородных алгебраических уравнений (46) имеет заведомо отличные
от нуля решения.
одновременно обратиться в нуль не могут, то
система трёх однородных алгебраических уравнений (46) имеет заведомо отличные
от нуля решения.
В этом случае определитель системы (46) должен равняться нулю:
![]()
Раскрывая определитель
(48), приходим к кубическому уравнению для определения трёх главных напряжений ![]() :
:
![]()
где коэффициенты:
![]()
![]()
![]()
являются инвариантами
тензора напряжений по отношению к преобразованиям координат x, y, z. Все три
корня уравнения (49) позволяют найти направляющие косинусы главных направлений
напряжённого состояния частицы тела. Поскольку из трёх уравнений (46) только
два независимы, то беря, например, два первых уравнения и решая их совместно с
(47) относительно ![]() по методу Крамера, получим:
по методу Крамера, получим:
![]()
где

В частном
случае плоской задачи ![]() и определитель
(48) приводит к уравнению
и определитель
(48) приводит к уравнению
![]()
откуда находим ранее полученную формулу
![]()
Полагая в (46)
![]() получим
систему уравнений:
получим
систему уравнений:
![]()
Умножая первое
уравнение на ![]() ,
а второе на
,
а второе на ![]() и вычитая, находим:
и вычитая, находим:
![]()
откуда, с
учётом ![]() ,
получим уже известную нам формулу (43):
,
получим уже известную нам формулу (43):
![]()
для
определения углов ![]() ,
характеризующих направление главных осей.
,
характеризующих направление главных осей.
Обзор различных типов напряженных состояний
При исследовании вопросов прочности в сложном напряженном состоянии существенное значение имеет вид напряженного состояния. Большинство материалов по-разному разрушается в зависимости от того, являются ли напряжения растягивающими или сжимающими. Как показывает опыт, все материалы без исключения способны воспринимать весьма большие напряжения в условиях всестороннего сжатия, в то время как при одноосном растяжении разрушение наступает при сравнительно низких напряжениях. Имеются напряженные состояния, при которых разрушение происходит хрупко, без образования пластических деформаций, а есть такие, при которых тот же материал способен пластически деформироваться.
В связи со сказанным очевидна необходимость более подробно остановиться на типовых признаках напряженных состояний и проследить, в каких условиях возникает то или иное состояние.
На основе такого обзора в дальнейшем проще будет ориентироваться в вопросах прочности и легче дать оценку степени опасности напряженного состояния материала. Выше было произведено деление напряженных состояний на трехосное, двухосное и одноосное. При решении вопросов прочности, однако, такая классификация не является достаточной и принято делить напряженные состояния на три класса в зависимости от знака главных напряжений.
К первому классу относятся трехосные растяжения, т. е. такие
напряженные состояния, в которых ни одно из главных напряжений не является
сжимающим. В частном случае все три главных растягивающих напряжения могут быть
равными; такое напряженное состояние называется чистым трехосным растяжением.
Оно возникает, например, в центральной части сплошного шара, быстро
нагреваемого извне (рис. 3.17.1, а).
Расширение внешних нагретых слоев приводит к тому, что внутренняя нагретая
область шара оказывается под воздействием всестороннего «растягивающего
давления». Круговые диаграммы при чистом трехосном растяжении вырождаются в
точку (рис. 3.17.1, а). Трехосное
растяжение, при котором два главных напряжения равны, но отличны от третьего,
возникает в точках, лежащих на оси растянутого образца, имеющего кольцевую
выточку (рис. 3.17.1,б). Весьма часто
встречается напряженное состояние, в котором ![]() ,
т. е. двухосное растяжение, также относящееся к рассматриваемому классу.
Двухосное растяжение, при котором
,
т. е. двухосное растяжение, также относящееся к рассматриваемому классу.
Двухосное растяжение, при котором ![]() ,
возникает, например, в быстровращающихся тонких дисках постоянной толщины (рис.
3.17.1, в). Равное двухосное
растяжение
,
возникает, например, в быстровращающихся тонких дисках постоянной толщины (рис.
3.17.1, в). Равное двухосное
растяжение ![]() возникает в точках, расположенных у внешней
поверхности сферического сосуда, нагруженного внутренним давлением (рис.
3.17.1, г). К рассматриваемому классу
напряженных состояний относится, наконец, и простое одноосное растяжение,
возникающее в однородном стержне при его растяжении или чистом изгибе (рис.
3.17.1, д).
возникает в точках, расположенных у внешней
поверхности сферического сосуда, нагруженного внутренним давлением (рис.
3.17.1, г). К рассматриваемому классу
напряженных состояний относится, наконец, и простое одноосное растяжение,
возникающее в однородном стержне при его растяжении или чистом изгибе (рис.
3.17.1, д).
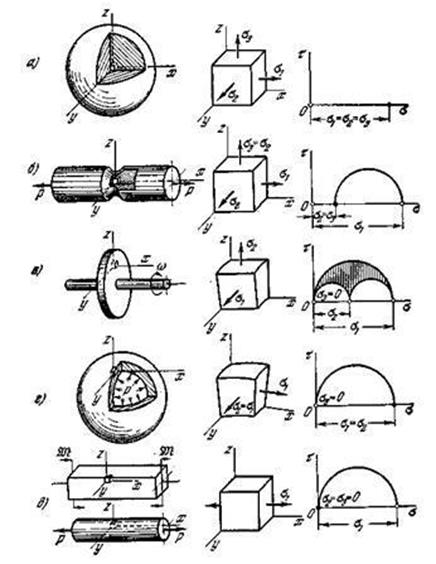
Рис.3.17.1
Второй распространенный класс составляют такие напряженные состояния, в
которых ни одно из главных напряжений не является растягивающим. Это — так
называемые трехосные сжатия. Для напряженных состояний этого класса
круговые диаграммы располагаются в левой части плоскости ![]() (рис.3.17.2).
(рис.3.17.2).
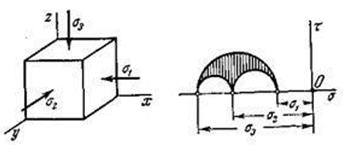
Рис.3.17.2
Чистое трехосное сжатие возникает в любом теле, независимо от его
формы, при всестороннем гидростатическом давлении (рис. 3.17.3, а). Неравномерное трехосное сжатие
характерно для точек, расположенных в окрестности контактирующих тел, таких,
как, например, ролики и обоймы подшипников, втулки и валы, и др. (рис. 3.17.3, б). Пример возникновения двухосного сжатия
показан на рисунке 3.17.3, в.
Двухосное равное сжатие (![]() )
возникает при нагружении давлением вала, имеющего свободные торцы (рис. 3.17.3,
г).
)
возникает при нагружении давлением вала, имеющего свободные торцы (рис. 3.17.3,
г).
Одноосное сжатие также относится к рассматриваемому классу напряженных состояний и возникает, в частности, при чистом изгибе и сжатии однородного стержня (рис. 3.17.3, д).
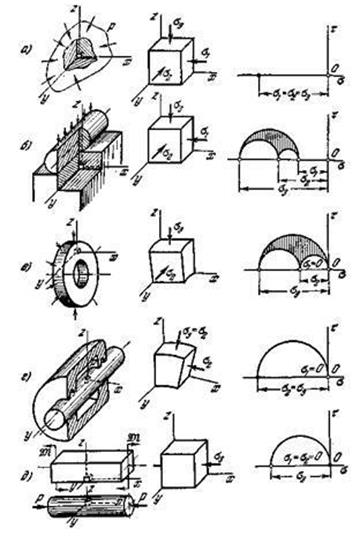
Рис.3.17.3
К третьему классу относятся так называемые смешанные напряженные
состояния, в которых наибольшее и наименьшее из главных напряжений имеют разные
знаки. Напряжение ![]() может быть положительным, так и отрицательным.
Круговые диаграммы напряженных состояний этого класса располагаются в средней
части плоскости
может быть положительным, так и отрицательным.
Круговые диаграммы напряженных состояний этого класса располагаются в средней
части плоскости ![]() (рис.3.17.4). Смешанное трехосное напряженное
состояние возникает, например, при нагружении толстостенного цилиндра
внутренним давлением (рис. 3.17.5, а).
Для изгибаемого и одновременно закручиваемого бруса характерно возникновение
двухосного смешанного напряженного состояния (рис. 3.17.5, б). Чистый сдвиг также представляет собой смешанное двухосное
напряженное состояние (рис. 3.17.5, в).
(рис.3.17.4). Смешанное трехосное напряженное
состояние возникает, например, при нагружении толстостенного цилиндра
внутренним давлением (рис. 3.17.5, а).
Для изгибаемого и одновременно закручиваемого бруса характерно возникновение
двухосного смешанного напряженного состояния (рис. 3.17.5, б). Чистый сдвиг также представляет собой смешанное двухосное
напряженное состояние (рис. 3.17.5, в).
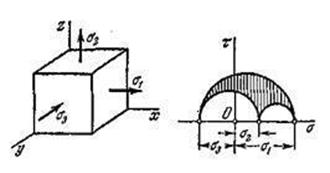
Рис.3.17.4
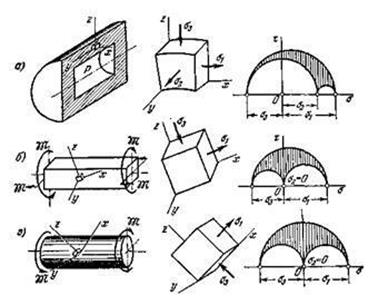
Рис.3.17.5
Пример
1.
Пусть ![]() .
Такое напряжённое состояние называется пространственным чистым сдвигом (рис.
3.18,а). Инварианты тензора
.
Такое напряжённое состояние называется пространственным чистым сдвигом (рис.
3.18,а). Инварианты тензора ![]() Кубическое уравнение:
Кубическое уравнение:
![]()
или, с учётом ![]() получаем
получаем
![]()
откуда
![]()
Если все
касательные напряжения ![]() ,
где k - предел текучести, то состояние частицы
называют полным пластическим.
,
где k - предел текучести, то состояние частицы
называют полным пластическим.
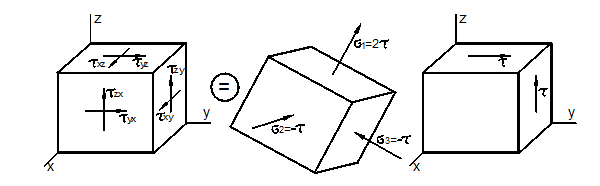
а)
б)
Рис. 3.18
При плоском
чистом сдвиге касательные напряжения ![]() параллельны одной плоскости xy (рис. 3.18,б). В этом случае, согласно диаграмме
чистого сдвига, частица тела переходит в пластическое состояние при
параллельны одной плоскости xy (рис. 3.18,б). В этом случае, согласно диаграмме
чистого сдвига, частица тела переходит в пластическое состояние при ![]() ,
где
,
где ![]() - предел текучести для плоского чистого сдвига. Такое состояние
частицы является неполным пластическим, т.к. в направлении z частица остаётся в упругом состоянии.
Заметим, что
- предел текучести для плоского чистого сдвига. Такое состояние
частицы является неполным пластическим, т.к. в направлении z частица остаётся в упругом состоянии.
Заметим, что ![]() .
.
Пример
2.
При растяжении
стержня напряжения ![]() (рис. 3.19).
(рис. 3.19).

а)
б)
Рис. 3.19
В этом случае
инварианты ![]() .
Кубическое уравнение (49) принимает вид:
.
Кубическое уравнение (49) принимает вид:
![]()
откуда находим
![]()
Пример
3.
Пусть
требуется найти главные напряжения, если все компоненты тензора напряжений
равны одной и той же величине ![]() .
В этом случае
.
В этом случае ![]() Из (49) получаем
Из (49) получаем ![]() Следовательно, заданное напряжённое состояние
представляет собой одноосное растяжение. Данное напряжённое состояние можно
разложить на напряжённое состояние всестороннего растяжения напряжениями
Следовательно, заданное напряжённое состояние
представляет собой одноосное растяжение. Данное напряжённое состояние можно
разложить на напряжённое состояние всестороннего растяжения напряжениями ![]() и пространственный чистый сдвиг с напряжениями
и пространственный чистый сдвиг с напряжениями
![]() .
Если считать объёмную деформацию упругой, т.е.
.
Если считать объёмную деформацию упругой, т.е. ![]() ,
то рассматриваемое напряжённое состояние за пределом упругости представляется
состоянием полной пластичности. Такое состояние возникает при одноосном
растяжении.
,
то рассматриваемое напряжённое состояние за пределом упругости представляется
состоянием полной пластичности. Такое состояние возникает при одноосном
растяжении.
Общее решение кубического уравнения для определения главных напряжений
Примем в (49) ![]() ,
где
,
где ![]() - главные значения девиатора напряжений. В
результате получим:
- главные значения девиатора напряжений. В
результате получим:
![]()
где коэффициенты:

являются инвариантами девиатора напряжений при преобразовании координатных осей.
Удобная форма ![]() получается прибавлением нулевого члена
получается прибавлением нулевого члена

к правой части
![]() В результате получаем
В результате получаем

или
![]()
где
использовано, что ![]()
Второй инвариант девиатора напряжений играет фундаментальную роль в сопротивлении материалов пластическому деформированию.
Величину
![]()
или

называют модулем тензора–девиатора напряжений.
Величину
![]()
называют модулем
тензора напряжений, а ![]() - модулем
шарового тензора напряжений.
- модулем
шарового тензора напряжений.
Общее решение кубического уравнения (52) в тригонометрической форме Кордано имеет вид:
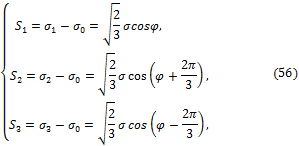
где угол ![]() называется фазой девиатора или углом вида
напряжённого состояния формоизменения. Для определения
называется фазой девиатора или углом вида
напряжённого состояния формоизменения. Для определения ![]() имеет место
соотношение:
имеет место
соотношение:
![]()
Определив ![]() из (57) находим по формулам (56) главные
напряжения
из (57) находим по формулам (56) главные
напряжения ![]() девиатора и тензора
напряжений.
девиатора и тензора
напряжений.
Эллипсоид напряжений Ламе
Пусть координатные оси в данной точке А тела совпадают с главными осями (рис. 3.20).

а)
б)
Рис. 3.20
Тогда на основании формул Коши получаем:
![]()
где
направляющие косинусы ![]() удовлетворяют соотношению:
удовлетворяют соотношению:
![]()
Подставляя в
это соотношение ![]() получим уравнение эллипсоида:
получим уравнение эллипсоида:
![]()
называемого эллипсоидом напряжений Ламе.
Так как ![]() -
координаты конца вектора напряжений, то конец этого вектора всегда находится на
поверхности эллипсоида с полуосями
-
координаты конца вектора напряжений, то конец этого вектора всегда находится на
поверхности эллипсоида с полуосями ![]() .
.
Эллипсоид Ламе (58) представляет собой геометрический образ напряжённого состояния частицы тела, т.е. тензора напряжений.
Тензор
напряжений можно представить как совокупность векторов напряжений ![]() в точке А на различно ориентированных площадках, т.е. своего рода
«ёжик» эллипсоидальной формы. Из рис. 3.20 видно, что главное напряжение
в точке А на различно ориентированных площадках, т.е. своего рода
«ёжик» эллипсоидальной формы. Из рис. 3.20 видно, что главное напряжение ![]() есть одновременно наибольшее значение полного
и максимального нормального напряжения
есть одновременно наибольшее значение полного
и максимального нормального напряжения ![]() ,
т.е.
,
т.е. ![]() .
Если
.
Если ![]() ,
то эллипсоид превращается в шар. Соответствующий тензор напряжений:
,
то эллипсоид превращается в шар. Соответствующий тензор напряжений:
![]()
называется
поэтому шаровым, а среднее напряжение ![]() -
его модулем.
-
его модулем.
Круги напряжений Мора
Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 3.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 3.21,а). Тогда, согласно (35), имеем:
![]()
Уравнения (59)
представляют собой параметрические уравнения окружности, каноническое уравнение
которой имеет в системе координат ![]() вид (рис. 3.22):
вид (рис. 3.22):
![]()
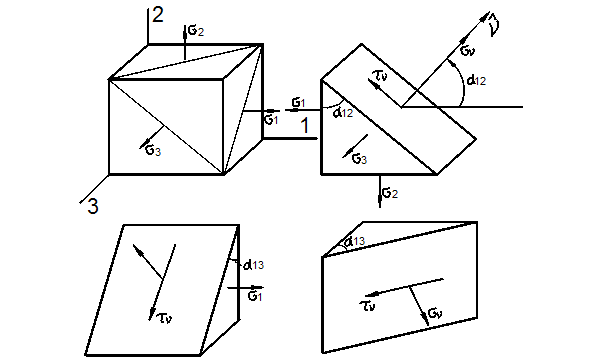
Рис. 3.21
Координаты
центра окружности ![]() радиус
радиус ![]() .
.

Рис. 3.22
Окружность Мора позволяет графически найти напряжение ![]() на любой площадке, положение
которой характеризуется углом
на любой площадке, положение
которой характеризуется углом ![]() . Для этого нужно отложить по часовой стрелке угол
. Для этого нужно отложить по часовой стрелке угол ![]() и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения
и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения ![]() . Наибольшее касательное напряжение возникает при
. Наибольшее касательное напряжение возникает при ![]() и равно численно радиусу
окружности Мора:
и равно численно радиусу
окружности Мора:
![]()
Минимальное
значение ![]() возникает на площадке при
возникает на площадке при ![]() и равно:
и равно:
![]()
Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 3.23).

Рис. 3.23
Их уравнения в параметрической форме имеют вид:

откуда следует, что наибольшее касательные напряжения в этих случаях:
![]()
также равны радиусам соответствующих кругов Мора.
Касательные напряжения:
![]()
носят название главных касательных напряжений. Они удовлетворяют тождеству
![]()
Каждой точке
на любой из окружности Мора отвечают напряжения ![]() и площадки, направление которой характеризуется
одним из углов
и площадки, направление которой характеризуется
одним из углов ![]() Те площадки, которые не содержат ни одну из
главных осей, окружностями Мора не описываются. Можно показать, что напряжения
на этих площадках задаются точками, расположенными между окружностями в заштрихованной
области. Из рис. 3.24 видно, что:
Те площадки, которые не содержат ни одну из
главных осей, окружностями Мора не описываются. Можно показать, что напряжения
на этих площадках задаются точками, расположенными между окружностями в заштрихованной
области. Из рис. 3.24 видно, что:
![]()
если принято
условие ![]()
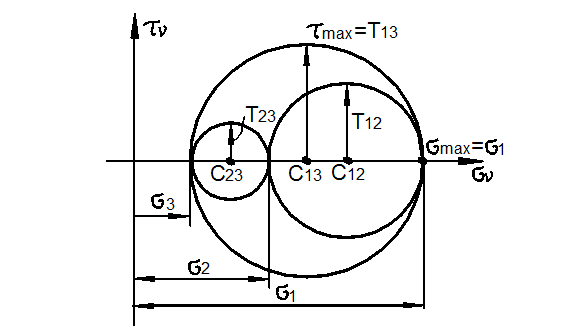
Рис. 3.24
Следовательно,
![]() определяется радиусом большого круга Мора.
Величину
определяется радиусом большого круга Мора.
Величину
![]()
называют параметром
вида напряжённого состояния Лоде. При
наложении на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения ![]() имеем
имеем ![]() ,
для сжатия
,
для сжатия ![]() имеем
имеем ![]() ,
для плоского чистого сдвига
,
для плоского чистого сдвига ![]() Соответствующие круги Мора приведены на рис.
3.25.
Соответствующие круги Мора приведены на рис.
3.25.
Таким образом,
параметр Лоде ![]() характеризует вид напряжённого состояния.
характеризует вид напряжённого состояния.
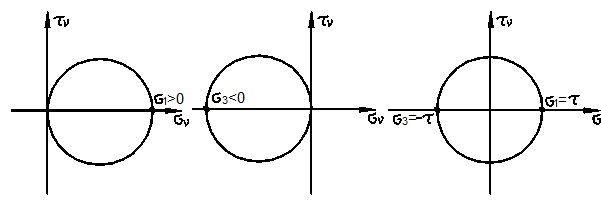
а)
б)
в)
Рис. 3.25
Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (35):
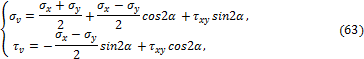
Поступая так же, как и в случае двухосного растяжения сводим параметрические уравнения окружности (63) к каноническому виду (рис. 3.26):
![]()
В (64) мы имеем более сложное выражение радиуса окружности:
![]()
При ![]() уравнение (64) сводится к (60) как частному
случаю.
уравнение (64) сводится к (60) как частному
случаю.
При ![]() построение круга Мора показано на рис. 3.26.
Сначала определяется положение центра С круга как точки с координатами
построение круга Мора показано на рис. 3.26.
Сначала определяется положение центра С круга как точки с координатами ![]()

Рис. 3.26
Затем
определяется положение точки А, характеризующей напряжения на грани x элемента при ![]() =0,
т.е.
=0,
т.е. ![]() .
Здесь следует помнить правило знаков для
.
Здесь следует помнить правило знаков для ![]() и других напряжений, указанных на рис. 3.12.
Заметим, что точки А
и В, характеризующие напряжения на
площадках, расположенных под углом 900 друг к другу, лежат на
противоположных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения
и других напряжений, указанных на рис. 3.12.
Заметим, что точки А
и В, характеризующие напряжения на
площадках, расположенных под углом 900 друг к другу, лежат на
противоположных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения ![]() на произвольной площадке, лежащей под углом
на произвольной площадке, лежащей под углом ![]() к оси x, можно определить следующим образом. Откладываем от точки А по часовой
стрелке угол
к оси x, можно определить следующим образом. Откладываем от точки А по часовой
стрелке угол ![]() 2 и определяем положение точки М на круге с искомыми координатами
2 и определяем положение точки М на круге с искомыми координатами ![]() .
Точка М’, диаметрально
противоположная Д, даёт напряжения
.
Точка М’, диаметрально
противоположная Д, даёт напряжения ![]() для площадки, составляющей угол 900
с той, которая имеет нормаль
для площадки, составляющей угол 900
с той, которая имеет нормаль ![]() ,
т.е. для площадки с углом
,
т.е. для площадки с углом ![]() с осью x. Точка Д даёт
максимальное касательное напряжение, равное радиусу круга Мора:
с осью x. Точка Д даёт
максимальное касательное напряжение, равное радиусу круга Мора:
![]()
Одной из
важных задач использования круга Мора является определение главных нормальных
напряжений ![]() и
и
![]() .
Этим напряжениям отвечают точки Р1 и Р2
круга. Из рис. 3.26 следует, что угол между направлениями на точки А и Р1 равен удвоенному углу
.
Этим напряжениям отвечают точки Р1 и Р2
круга. Из рис. 3.26 следует, что угол между направлениями на точки А и Р1 равен удвоенному углу ![]() ,
определяющему первое главное напряжение, а угол между направлениями А и Р2
– удвоенный угол
,
определяющему первое главное напряжение, а угол между направлениями А и Р2
– удвоенный угол ![]() ,
определяющий второе главное направление. Имеет место соотношение
,
определяющий второе главное направление. Имеет место соотношение
![]()
которое совпадает с формулой (36).
Из изложенного следует, что круг Мора можно использовать в качестве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напряжений.
Напряжения на октаэдрических площадках
Рассмотрим площадки, равнонаклонённые к главным осям (рис. 3.27,а). Такие площадки называются октаэдрическими. Они образуют геометрическую фигуру, называемую главным октаэдром (восьмигранником) (рис. 3.27,б).
Для первого октаната, образуемого положительными направлениями главных
осей, направляющие косинусы ![]() . Поэтому из формул Коши (29) следует:
. Поэтому из формул Коши (29) следует:
![]()
Нормальное напряжение, согласно (31), равно:
![]()
т.е. равно среднему напряжению.
а)
б)
Рис. 3.27
Касательное напряжение находим по формуле
![]()
Заменяя ![]() их выражениями (66), (67) получим:
их выражениями (66), (67) получим:
![]()
Направление
действия ![]() определяется углом виды напряжённого состояния
определяется углом виды напряжённого состояния
![]() на октаэдрической площадке (рис. 3.28),
который совпадает с фазой напряжённого состояния. На рис. 3.28 занумерованные
направления со штрихами представляют собой проекции главных направлений на октаэдрическую плоскость.
на октаэдрической площадке (рис. 3.28),
который совпадает с фазой напряжённого состояния. На рис. 3.28 занумерованные
направления со штрихами представляют собой проекции главных направлений на октаэдрическую плоскость.
Угол ![]() связан с параметром Лоде
связан с параметром Лоде ![]() простым соотношением:
простым соотношением:
![]()
Для
растяжения ![]() сжатия
сжатия ![]() для чистого сдвига
для чистого сдвига ![]()
Таким образом,
на всех гранях главного октаэдра действуют одинаковые нормальные напряжения ![]() (67) и одинаковые касательные напряжения
(67) и одинаковые касательные напряжения ![]() (68).
(68).

Рис. 3.28
Первые подвергают октаэдр всестороннему растяжению или сжатию, что можно сравнить с давлением воды на погружённый в неё октаэдр. Вторые приводят к изменению формы октаэдра и к его пластическому деформированию. Октаэдрическое касательное напряжение не изменяется, если наложить на частицу всестороннее растяжение – сжатие. С точностью до множителя модуль девиатора напряжений:
![]()
и этим самым, с точностью до постоянного множителя, определяет его физический смысл.
Введём два
важных понятия о простом (пропорциональном) и сложном нагружении.
Нагружение назовём простым (пропорциональным), если все компоненты тензора
напряжений изменяются пропорционально одному параметру t, т.е. ![]() В этом случае параметр Лоде
В этом случае параметр Лоде ![]() и угол вида (фаза) напряжённого состояния
и угол вида (фаза) напряжённого состояния ![]() остаются неизменными. В противном случае
нагружение называют сложным. Эти понятия были введены великим русским
учёным-механиком, профессором Московского государственного университета А.А.
Ильюшиным (1911 – 1999).
остаются неизменными. В противном случае
нагружение называют сложным. Эти понятия были введены великим русским
учёным-механиком, профессором Московского государственного университета А.А.
Ильюшиным (1911 – 1999).
Определение удлинений и сдвигов для произвольно направленных волокон
Рассмотрим частицу тела, отнесённую к координатным осям x, y, z (рис. 3.29).

а)
б) в)
Рис. 3.29
Направление диагонали ОА = dS определим до деформации единичным вектором:
![]()
а после
деформации – единичным вектором ![]() ,
повёрнутым на угол
,
повёрнутым на угол ![]() .
После деформации длина волокна изменится и станет равной ОА’ = dS’ , так, что будет выполнено векторное
равенство:
.
После деформации длина волокна изменится и станет равной ОА’ = dS’ , так, что будет выполнено векторное
равенство:
![]()
Волокно ОА получит относительную деформацию:
![]()
откуда
![]()
Соотношение (70), с учётом (71), (72), запишем в виде:
![]()
Соотношение
(73) названо профессором Л.А. Толоконниковым (1923 – 1998) фундаментальным соотношением теории
деформаций.
Так как вектор перемещения
![]()
то
![]()
где

![]()
Возводя (73) в квадрат, получим:
![]()
Считая деформации малыми по сравнению с единицей и пренебрегая в (76) нелинейными членами, находим:
![]()
Учитывая (69), (74), (75) и производя скалярное умножение, находим:
![]()
где обозначено:

Формулы (79) связывают компоненты малой линейной деформации и перемещения и носят название геометрических соотношений Коши для деформаций.
Рассмотрим теперь два ортогональных волокна, направление которых характеризуется единичными векторами:
![]()
где
![]()
![]()
Для них можно составить два фундаментальных соотношения (рис. 3.29,в):
![]()
Для
производной ![]() имеем соотношение (74), а для
имеем соотношение (74), а для
![]() аналогичное соотношение с заменой ds на dt.
аналогичное соотношение с заменой ds на dt.
В результате перемножения соотношений (80) получим:
![]()
Считая деформации малыми и пренебрегая нелинейными слагаемыми, находим:
![]()
Легко установить геометрический смысл введённых в формулах Коши (79) обозначений, названных компонентами малой линейной деформации.
Пусть мы имеем
волокно dx. Для него ![]()
Из (79)
получаем ![]() Следовательно,
Следовательно, ![]() есть действительно относительное удлинение
частицы вдоль оси x.
Аналогично выясняется геометрический смысл компонент деформации
есть действительно относительное удлинение
частицы вдоль оси x.
Аналогично выясняется геометрический смысл компонент деформации ![]() .
.
Пусть теперь
мы имеем два ортогональных волокна dx и dy. Тогда для первого ![]() а для второго
а для второго ![]() Из (81) получаем
Из (81) получаем ![]() Следовательно,
Следовательно, ![]() представляет собой половины сдвига между
волокнами dx и dy. Аналогично можно выяснить геометрический смысл остальных компонент:
представляет собой половины сдвига между
волокнами dx и dy. Аналогично можно выяснить геометрический смысл остальных компонент: ![]() и
и ![]()
В частном
случае плоской деформации ![]() имеем:
имеем:
![]()
и из формул (78), (81) следуют полученные нами ранее формулы

Формулы Коши
(35) можно получить значительно проще. Рассмотрим одну из граней ОАСВ частицы тела в плоскости ху со сторонами dx
и dy (рис. 3.30). В результате малой линейной
деформации эта грань элемента удлинится в направлениях осей х, у и изменит прямой угол на величину
деформации сдвига ![]()
Рассмотрим деформацию волокна ОА = dx. Её можно вычислить следующим образом. Представим сначала, что волокно переместилось в положение О/А/ = dx как жёсткое целое, сохранив свою длину. Затем волокно удлинилось на величину А//А/// и по перпендикуляру А///А/ перешло в положение ОА/.
В соответствии с принципом малости перемещений перемещение А///А/ не вызывает дополнительного удлинения волокна ОА.

Рис. 3.30
Поэтому
![]()
Аналогично можно найти деформации в направлениях осей y и z:
![]()
Рассмотрим
теперь деформацию сдвига между волокнами
ОА и ОВ (рис. 3.30). Малые углы
поворота ![]() и
и ![]() волокон отождествим с их тангенсом. Тогда:
волокон отождествим с их тангенсом. Тогда:

где считается ![]() в силу малости относительных деформаций по
сравнению с единицей.
в силу малости относительных деформаций по
сравнению с единицей.
Таким образом:
![]()
Аналогично находим деформации сдвига (угловые деформации) в двух других координатных плоскостях.
В результате получаем шесть геометрических зависимостей Коши между компонентами тензора деформации и составляющих перемещения:
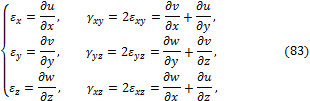
Деформации ![]() считаются положительными, если отвечают
удлинениям волокон, и отрицательными, если они укорачиваются. Положительные
сдвиги отвечают уменьшению прямого угла между положительными направлениями
координатных осей. Отрицательные сдвиги отвечают увеличению прямого угла между
этими же волокнами.
считаются положительными, если отвечают
удлинениям волокон, и отрицательными, если они укорачиваются. Положительные
сдвиги отвечают уменьшению прямого угла между положительными направлениями
координатных осей. Отрицательные сдвиги отвечают увеличению прямого угла между
этими же волокнами.
Объёмная деформация
![]()
т.е. может быть выражена через составляющие перемещения.
Главные деформации и сдвиги
Поставим
вопрос об отыскании таких направлений в данной точке тела, в которых волокна
испытывают экстремальные удлинения, а сдвиг отсутствует. Такие направления
назовём главными направлениями деформации, а сами деформации – главными
деформациями. Обозначим их ![]() Пусть
Пусть ![]() - направляющие косинусы главного направления,
удовлетворяющие условию:
- направляющие косинусы главного направления,
удовлетворяющие условию:
![]()
Составим функцию Лагранжа:
![]()
и условия экстремума этой функции. Получим систему трёх однородных алгебраических уравнений:

Приравнивая к нулю определитель системы (85), получаем:
![]()
Раскрывая этот определитель, приходим к кубическому уравнению для определения главных удлинений:
![]()
где обозначено:
![]()
![]()
![]()
Величины ![]() являются инвариантами тензора деформаций по
отношению к повороту координатных осей. Направления волокон,
испытывающих главные удлинения называются главными направлениями или осями
деформации. Они взаимно ортогональны и сдвигов между ними не
происходит.
являются инвариантами тензора деформаций по
отношению к повороту координатных осей. Направления волокон,
испытывающих главные удлинения называются главными направлениями или осями
деформации. Они взаимно ортогональны и сдвигов между ними не
происходит.
В частном
случае плоской деформации ![]() Из (87) следует уравнение
Из (87) следует уравнение
![]()
откуда находим:
![]()
Система (85)
при ![]() принимает вид
принимает вид
![]()
откуда следует формула
![]()
для определения главных направлений деформации.
Аналогично кругам напряжений Мора имеют место круги деформации Мора. Параметрические уравнения наибольшего из кругов Мора имеют вид:

Из (91) следует каноническое уравнение окружности Мора для деформации:
![]()
На рис. 3.31 дано геометрическое изображение кругов деформаций Мора, из которых следует:
![]()
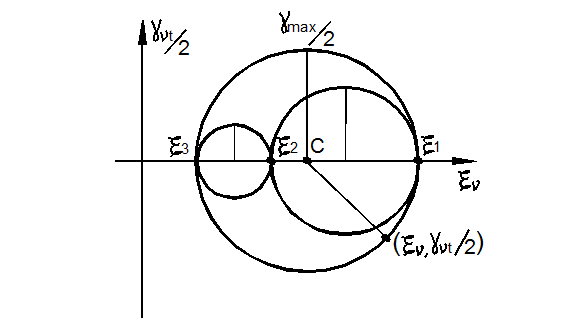
Рис. 3.31
Величина:
![]()
называется параметром Лоде для деформированного состояния. Она характеризует вид деформированного состояния.
Радиусы кругов Мора дают экстремальные значения сдвигов:
![]()
которые называются главными сдвигами.
В соответствии с законом Гука (15) и с учётом (61), (93) получаем:
![]()
Общее решение кубического уравнения для определения главных деформаций
Как и при
определении главных напряжений, сделаем в уравнении (87) замену ![]() где Эк
– главные деформации тензора- девиатора
деформаций. В результате получим:
где Эк
– главные деформации тензора- девиатора
деформаций. В результате получим:
![]()
где коэффициенты:

являются инвариантами относительно поворота координатных осей x, y, z.
Фундаментальную роль в сопротивлении материалов играет второй инвариант. Величину
![]()
или

называют модулем тензора–девиатора деформаций. Величину
![]()
называем модулем тензора деформаций.
Общее решение кубического уравнения (65) имеет вид:
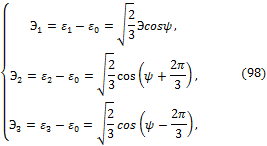
где угол ![]() называется фазой девиатора
или углом вида деформированного состояния формоизменения. Для определения
называется фазой девиатора
или углом вида деформированного состояния формоизменения. Для определения ![]() имеет место соотношения:
имеет место соотношения:
![]()
Определив из
(99) ![]() ,
находим по формулам (98) главные деформации Эк и
,
находим по формулам (98) главные деформации Эк и ![]() девиатора и тензора деформаций.
девиатора и тензора деформаций.
Угол ![]() связан с параметром Лоде
связан с параметром Лоде
![]() соотношением:
соотношением:
![]()
Модуль Э девиатора
деформаций имеет простой геометрический смысл. С точностью до множителя Э совпадает с октаэдрическим сдвигом, т.е. ![]() .
Под октаэдрическим сдвигом понимается сдвиг между октаэдрическими волокнами, которые равнонаклонены
к главным осям. Модули девиаторов деформаций Э и напряжений
.
Под октаэдрическим сдвигом понимается сдвиг между октаэдрическими волокнами, которые равнонаклонены
к главным осям. Модули девиаторов деформаций Э и напряжений ![]() связаны простым соотношением (26).
связаны простым соотношением (26).
Из закона Гука (15) для главных направлений имеем:
![]()
тогда
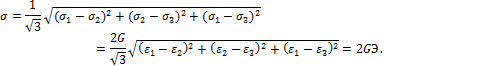
Дифференциальные уравнения равновесия Коши
Для равновесия тела необходимо и достаточно, чтобы каждая его частица находилась в равновесии. Выделим из тела материальную частицу в форме параллелепипеда со сторонами dx, dy, dz (рис. 3.32).
Действие отброшенной части тела заменим напряжениями, равномерно распределёнными по его граням. Напряжения на противоположных гранях могут отличаться на малые частные приращения вследствие приращения координат.

Рис. 3.32
Составим три уравнения равновесия в проекциях на оси x, y, z.
Проецируя все силы на ось х, получаем:

где ![]() – проекция объёмной силы.
– проекция объёмной силы.
Аналогично можно записать уравнения равновесия в направлении осей y и z. После сокращений три уравнения равновесия Коши принимают вид:
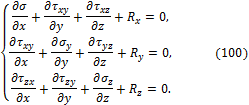
Составим ещё три уравнения равновесия моментов относительно осей x, y, z. Сумма моментов относительно оси х равна:
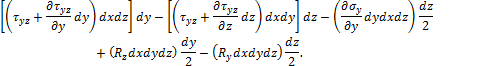
Аналогично можно записать ещё два уравнения равновесия моментов относительно осей y и z.
Сокращая на dxdydz и пренебрегая бесконечно малыми величинами высшего порядка, получаем закон парности касательных напряжений:
![]()
Система уравнений равновесия (100) Коши представляет собой дифференциальные уравнения равновесия в напряжениях. Они показывают с учётом (101), что задача определения напряжений трижды статически неопределима. При интегрировании уравнений (100) появятся произвольные функции, для определения которых используются статические граничные условия:

Иногда удобно иметь уравнения равновесия в перемещениях. Согласно закону Коши – Гука (21) и соотношений (83):
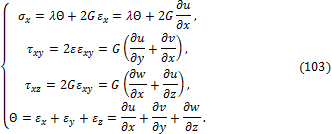
Подставляя (103) в первое уравнение (100), получим уравнение:
![]()
где
![]()
Аналогично получаются два других уравнения. В результате вместо (100) получаем систему уравнений Ламе в перемещениях:

где
![]()
дифференциальный оператор Лапласа.
При интегрировании уравнений (104) используются геометрические граничные условия вида:
![]()
на поверхности
тела ![]() .
.
Уравнение совместности деформаций
Компонент
тензора малых линейных деформаций Коши (83) можно рассматривать как систему
шести дифференциальных уравнений в частных производных для определения трёх
компонент перемещений u,
v, w. При произвольном выборе ![]() система (83) не имеет решения. Компоненты
деформации должны удовлетворять шести соотношениям интегрируемости уравнений
(83), которые носят название уравнений совместности деформаций Сен- Венана.
система (83) не имеет решения. Компоненты
деформации должны удовлетворять шести соотношениям интегрируемости уравнений
(83), которые носят название уравнений совместности деформаций Сен- Венана.
Они имеют вид:
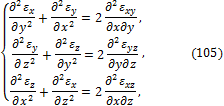

При подстановке в соотношения (105), (106) выражений (83) для деформаций они обращаются в тождества. Поэтому их иногда называют тождествами Сен-Венана.
Получим, например, первое из соотношений (100):
![]()
Аналогично можно получить другие соотношения.
Подставляя в (105), (106) вместо компонент деформации их выражения согласно обобщённому закона Гука (20) и, используя уравнения равновесия Коши, можно получить уравнения совместности деформации Бельтрами через составляющие напряжений.
При отсутствии объёмных сил эти уравнения имеют вид:

![]() - среднее напряжение.
- среднее напряжение.
Кручение призматических стержней произвольного поперечного сечения
Рассмотрим стержень произвольного сплошного поперечного сечения, который закреплён на одном конце и скручивается моментом М на другом (рис. 3.33).

Рис. 3.33
Вводим гипотезу жёсткого контура, согласно которой контур сечения поворачивается как жёсткое целое, а площадь сечения может исказиться.
Под действием момента правое свободное торцевое сечение повернётся относительно левого на угол:
![]()
где ![]() - угол закручивания на единицу длины.
Перемещения u и v
произвольной точки А
в плоскости сечения:
- угол закручивания на единицу длины.
Перемещения u и v
произвольной точки А
в плоскости сечения:
![]()
Так как гипотеза плоских сечений в общем случае произвольного сечения на выносливость, осевое перемещение
![]()
где функция ![]() называется функцией кручения Сен-Венана.
Она характеризует искажение (депланацию) поперечного
сечения.
называется функцией кручения Сен-Венана.
Она характеризует искажение (депланацию) поперечного
сечения.
Согласно (109), (110) и соотношениям Коши (83) получаем:
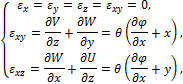
В соответствии с обобщённым законом Гука (21) находим:
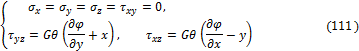
Считая в уравнениях равновесия Коши (100) объёмные силы равными нулю и подставляя в них выражения (111), получим, что первые два уравнения тождественно удовлетворятся, а третье примет вид:
![]()
Полученное уравнение в частных производных (112) называется гармоническим уравнением Лапласа.
На боковой
поверхности стержня внешние силы ![]() и граничные условия (102) принимают вид
и граничные условия (102) принимают вид
![]()
или
![]()
Крутящий момент в поперечном сечении
![]()
где
![]()
- геометрическая жёсткость стержня при кручении.
Из (114) следует:
![]()
Полное касательное напряжение:
![]()
где ![]()
Из (117),
(118) видно, что ![]() возникает при
возникает при ![]() в опасной точке сечения, которая не
обязательно наиболее удалённая.
в опасной точке сечения, которая не
обязательно наиболее удалённая.
Таким образом,
задача о кручении призматического стержня сводится к решению гармонического
уравнения (112) для функции ![]() с граничным условием (113) на контуре L поперечного сечения.
Предложенный метод решения называется полуобратным
методом Сен-Венана, в котором часть искомых величин задаётся, а
остальные неизвестные определяются из общих уравнений теории упругости при заданных статических граничных условий.
с граничным условием (113) на контуре L поперечного сечения.
Предложенный метод решения называется полуобратным
методом Сен-Венана, в котором часть искомых величин задаётся, а
остальные неизвестные определяются из общих уравнений теории упругости при заданных статических граничных условий.
Можно вместо
функции кручения ![]() ввести функцию напряжений F(x,y) Прандтля:
ввести функцию напряжений F(x,y) Прандтля:
![]()
В этом случае все три уравнения равновесия Коши будут тождественно удовлетворены. Составим гармоническую операцию над F.
С учётом (119) получаем:
![]()
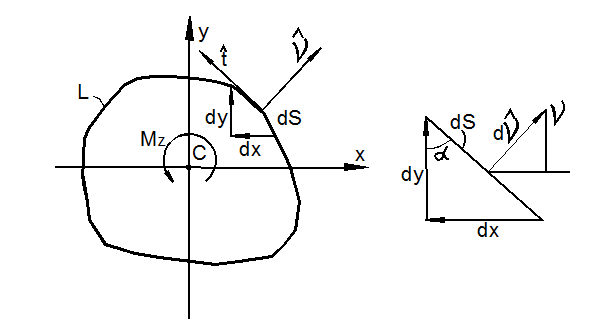
Уравнение (120) называется уравнением Пуассона. Граничные условия:
![]()
с учётом ![]() (рис. 3.34) преобразуется к виду
(рис. 3.34) преобразуется к виду
![]()
или
![]()
на контуре L поперечного сечения.
а)
б)
Рис. 3.34
Крутящий момент (114) может быть представлен в виде
![]()
Таким образом, задача о кручении в напряжениях сводится к нахождению функции напряжений F из уравнения Пуассона при граничном условии F = 0 на контуре поперечного сечения.
Кручение стержня эллиптического сечения
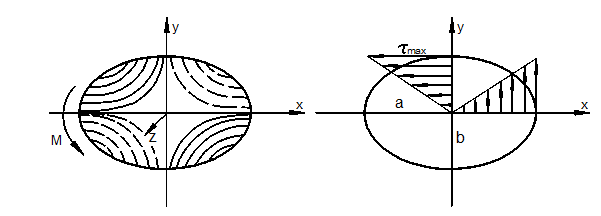
В качестве примера рассмотрим стержень эллиптического сечения (рис. 3.35).
а)
б)
Рис. 3.35
Уравнение контура эллипса:
![]()
Для функции напряжений примем выражение
![]()
которое удовлетворяет граничному условию F = 0, на контуре сечения.
Подставляя выражение (123) в уравнение Пуассона (120), получим:
![]()
Крутящий момент, согласно (122), равен:
![]()
откуда
![]()
Напряжения (119):
![]()
Полное напряжение (117):
![]()
Или
![]()
Распределение напряжений показано на рис. 3.35,б. Максимальное напряжение имеет место на концах малой оси эллипса.
Кручение стержня прямоугольного сечения
Рассмотрим сначала стержень узкого прямоугольного поперечного сечения (рис. 3.36,а).

а)
б)
Рис. 3.36
В этом случае
будем пренебрегать выполнением граничных условий на коротких сторонах при ![]() .
Примем функцию напряжений в виде
.
Примем функцию напряжений в виде
![]()
В таком виде
граничное условие F = 0 на длинных сторонах при ![]() будет удовлетворено.
будет удовлетворено.
Подставляя
предполагаемое решение в уравнение (120) Пуассона, получим ![]() .
Напряжения (119):
.
Напряжения (119):
![]()
Полное напряжение (117):
![]()
где r=2x.
Крутящий
момент ![]() (122):
(122):
![]()
где
![]()
Из (125), (126) следует:
![]()
Максимальное
напряжение имеет место в середине длинной стороны сечения, где ![]() :
:
![]()
где
![]()
- момент сопротивления узкого прямоугольного сечения.
Пусть теперь отношение сторон h/b одного порядка. Решение уравнения Пуассона представим в виде:
![]()
где первое
слагаемое представляет его частное решение, а второе – решение однородного
уравнения Лапласа ![]() в форме Фурье. На контуре сечения F = 0. Поэтому граничные условия можно записать в виде:
в форме Фурье. На контуре сечения F = 0. Поэтому граничные условия можно записать в виде:

Подставляя (131) в уравнение Пуассона (120), получим:
![]()
откуда, разделяя переменные:
![]()
или
![]()
Решения этих уравнений имеют вид:
![]()
Удовлетворяя
полученное решение граничным условиям (132) и учитывая симметрию функций X(x), Y(y)
относительно осей х, у, получим, что А = 0, С = 0, ![]() откуда следует
откуда следует ![]() где i = 1,2,3,….
где i = 1,2,3,….
В результате функция F принимает вид
![]()
Далее, согласно (122), вычисляем:
![]()
где

Напряжения (119):
![]()
где

![]()
или
![]()
а величины ![]() определяются согласно (136).
определяются согласно (136).
Наибольшее
значение ![]() имеет место при h > b в середине длинной стороны при
имеет место при h > b в середине длинной стороны при ![]() .
В этом случае
.
В этом случае ![]()
![]()
где
![]()
-
геометрический момент сопротивления кручению, ![]() .
.
![]()
Для практических расчётов достаточно взять i = 1, т.е. сохранив в рядах одно слагаемое.
Для вычисления
![]() в середине короткой стороны следует принять в
(136)
в середине короткой стороны следует принять в
(136) ![]() . В результате получим
. В результате получим ![]()
![]()
Значения
коэффициентов ![]() в зависимости от отношения сторон h/b приведены
в справочных данных.
в зависимости от отношения сторон h/b приведены
в справочных данных.
Таким образом, мы показали, что задача о кручении стержня прямоугольного сечения может быть решена строгими методами теории упругости.
Кручение стержня треугольного сечения
Рассмотрим стержень с равносторонним треугольным сечением (рис. 3.37).

Рис. 3.37
Контур сечения определяется уравнением
![]()
Примем функцию
депланации ![]() в виде
в виде
![]()
Она
удовлетворяет уравнению Лапласа ![]() и поэтому является решением задачи Сен-Венана
о кручении.
и поэтому является решением задачи Сен-Венана
о кручении.
Подставляя (142) в граничные условия (113), получаем:
![]()
откуда следует:
![]()
где С – постоянная интегрирования.
Если в (143)
положить ![]() ,
то получим:
,
то получим:
![]()
Первая часть полученного уравнения (144) представляет собой произведение левых частей уравнений сторон равностороннего треугольника (рис. 3.37). Поэтому контурные условия всегда выполняются.
Вычислим геометрическую жёсткость:
![]()
Интегрирование
по x ведётся от ![]() до x=a и по y от нуля до
до x=a и по y от нуля до ![]() .
В результате получим:
.
В результате получим:
![]()
где ![]()
Относительный угол поворота:
![]()
Вычисляем напряжения:

Полагая x=a, y=0, получаем:
![]()
Эпюра ![]() для у = 0 показана на рис. 3.37.
для у = 0 показана на рис. 3.37.
Вопросы для самопроверки
- Что понимается под напряженным состоянием в точке твердого тела, если оно нагружено внешними силами?
- Объясните понятие тензор напряжений?
- Какие напряжения называются главными?
- Чем характеризуется и как изображается напряженное состояние в точке?
- Какие площадки и какие напряжения называют главными?
- Чем характеризуется деформированное состояние в точке?
- Сколькими параметрами определяется плоское напряженное состояние точки? Назовите эти параметры?
- В каких случаях возникают предельные напряженные состояния у пластичных и хрупких материалов?
- Сформулируйте закон парности касательных напряжений?
- Какие существуют типы напряженного состояния в точке тела, чем они отличаются?
- Что понимается под линейным напряженным состоянием?
- Что понимается под плоским напряженным состоянием?
- Что понимается под объемным напряженным состоянием?
- Какое напряженное состояние называется пространственным (трехосным), плоским (двухосным) и линейным (одноосным)?
- Понятие о сложном напряженном состоянии.
- Дайте определение главных площадок и главных напряжений. Получите выражения для определения положения главных площадок и величин главных напряжений?
- Какие площадки называются главными?
- Соотношение между главными напряжениями.
- Каково правило законов для нормальных и касательных напряжений?
- Чему равна сумма нормальных напряжений, действующих на любых двух взаимно перпендикулярных площадках?
- Что такое главные напряжения и главные площадки? Как расположены главные площадки относительно друг друга?
- Чему равны касательные напряжения на главных площадках?
- Как вычислить максимальные касательные напряжения в точке тела при одноосном напряженном состоянии? По каким площадкам они действуют?
- Как вычислить максимальные нормальные и касательные напряжения при плоском и объемном напряженных состояниях?
- Как связаны главные напряжения и максимальные касательные напряжения при чистом сдвиге?
- Как определить значение главных напряжений при плоском напряженном состоянии?
- Напишите формулы для определения главных напряжений и углов наклона главных площадок.
- Как
определить положение главной площадки, по которой действует главное напряжение ![]() в общем случае плоского напряженного
состояния?
в общем случае плоского напряженного
состояния?
- Чему равны максимальные значения касательных напряжений в случае плоского напряженного состояния?
- Какие площадки называются площадками сдвига и под каким углом они наклонены к главным площадкам?
- Чему равна сумма нормальных напряжений на любых трех взаимно перпендикулярных площадках?
- Чему равны
максимальные и минимальные касательные напряжения (при заданных напряжениях ![]() )
и по каким площадкам они действуют?
)
и по каким площадкам они действуют?
- Докажите свойство парности (взаимности) касательных напряжений и получите выражения для нормального и касательного напряжения в наклонной площадке?
- Какими выражениями определяются величины экстремальных касательных напряжений и как расположены площадки, в которых они действуют?
- Докажите возможность определения напряжений на наклонной площадке, пользуясь кругом напряжений (Мора)?
- Опишите последовательность построения круга напряжений (Мора) и технику определения с помощью его главных напряжений и главных площадок, величин экстремальных касательных напряжений и площадок, в которых они действуют?
- Получите выражения для относительных линейных деформаций по координатным направлениям при объемном напряженном состоянии? Сформулируйте обобщение этих выражений на случай определения линейных деформаций по произвольному направлению при плоском напряженном состоянии?
- Получите выражение относительной объемной деформации в точке через напряжения?
- Докажите, что коэффициент Пуассона не может быть более 0,5?
- Получите выражение удельной потенциальной энергии в точке через главные напряжения?
- Какие напряженные состояния называются предельными?
- Как определяются предельные состояния при линейном напряженном состоянии?
- Почему нельзя экспериментально исследовать предельные состояния при сложных напряженных состояниях (плоском или объемном)?
- Что представляет собой обобщенный закон Гука?
- Какое напряженное состояние в точке считают предельным?
- Какие напряженные состояния в точке называют подобными?
- Напишите формулы обобщенного закона Гука?
- Какая разница между прямой и обратной задачей при исследовании напряженного состояния твердого тела?
- Как можно определить нормальное и касательное напряжения в наклонной площадке с помощью круга Мора?
- Что понимается под обобщенным законом Гука? Как он записывается аналитически?
- Какая зависимость существует между модулями продольной Е и поперечной G упругости?
- На основе какого из допущений, принятых в курсе сопротивления материалов, получен обобщенный закон Гука?
- Что называется полной удельной потенциальной энергией деформации, удельной потенциальной энергией изменения объема и формы?
- Как определяется потенциальная энергия упругой деформации при линейном и объемном напряженном состоянии?
- Из каких составляющих складывается полная потенциальная энергия твердого тела?
- Какой случай плоского напряженного состояния называется чистым сдвигом?
- Напишите закон Гука при сдвиге.
- Докажите, что объемная деформация при чистом сдвиге равна нулю.
- Напишите зависимость между модулем упругости Е и модулем сдвига G.
- Какой случай напряженного состояния называется чистым сдвигом и каковы его особенности?
- Опишите деформацию при чистом сдвиге и сформулируйте закон Гука при сдвиге.
- Что называется модулем упругости при сдвиге и какова его размерность?
- Получите соотношение между упругими постоянными изотропных тел Е, G, v?
- Что называется предельным опасным состоянием материала? Чем характеризуется наступление опасного состояния для пластичных и хрупких материалов?
- Какая точка тела называется опасной?
- Что называется допускаемым напряженным состоянием?
- Почему определение прочности в случаях сложного (плоского или пространственного) напряженного состояния приходится производить на основе результатов опытов, проводимых при одноосном напряженном состоянии?
- Понятие о теориях (гипотезах) прочности.
- Какие теории (гипотезы) прочности применяются наиболее часто?
- Что представляют собой теории прочности?
- Для чего служат теории прочности?
- Сформулируйте первую и вторую теории прочности. Укажите область применения.
- Сформулируйте третью и четвертую теории прочности? Укажите область применения этих теорий.
- Какие теории прочности считаются классическими?
- На каких предположениях основаны первая, вторая, третья, четвертая и пятая теории прочности? Кто является их основоположниками?
- Какие теории прочности считаются рабочими?
- Какая из теорий используется при расчете конструкций из анизотропных материалов?
- Как определить меридиональные и окружные напряжения в тонкостенной оболочке, находящейся под действием внутреннего давления газа?
Онлайн-калькулятор "Расчет по различным теориям прочности"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов