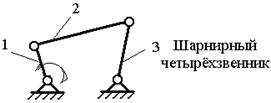
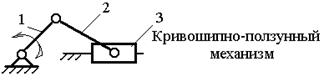
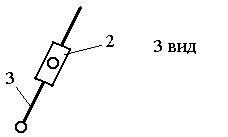
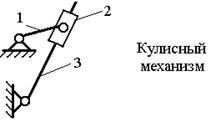
Главная

Лекция 2. Структура механизмов.

Система – полный, целостный набор элементов, взаимосвязанных между собой так, чтобы могла реализоваться функция системы.

В любой научной теории переход от описания к объяснению, от явлений к сущности, от формы к содержанию совпадает с познанием структуры исследуемых систем и процессов, с переходом от одних структурных уровней к другим, более глубоким. Структура – строение и внутренняя форма организации системы, выступающая как единство устойчивых взаимосвязей между ее элементами, а также законов данных взаимосвязей. Структура – неотъемлемый атрибут всех реально существующих объектов и систем. Связь элементов в структуре подчиняется диалектике взаимоотношения части и целого.

Все многообразие существующих механизмов можно представить как внешнее проявление состояния внутренних параметров системы, имя которой механизм. Для изучения этих параметров удобно и естественно использовать структурные модели различного уровня сложности.

Знакомство с механизмом начинается с выделения его составных частей и определения связей между ними, т.е. с изучения структуры.

От структуры зависят вид и все основные свойства механизма, например, механическая система в зависимости от ее строения может быть манипулятором, имитирующим движение руки человека, зубчатым механизмом или статически неопределенной фермой. Поэтому естественно, что структурная теория является одним из фундаментальных разделов теории механизмов и машин.

Структурная теория как подсистема теории механизмов дает возможность понять законы строения и работу механизма и на этой основе строить его расчетные схемы; проектировать схему механизма по заданным свойствам, судить о технологичности существующих и вновь создаваемых конструкций механизмов и их эксплуатационных свойствах; систематизировать механизмы и с помощью классификаций охватить все их многообразие; использовать аналогичные методы анализа и синтеза для родственных групп механизмов. Целью учения о структуре как системы является познание составных частей механизма и связей между ними, отражающих их взаимодействие, а также общих методов исследования строения механизма (структурный анализ) и проектирования его структуры по заданным свойствам (структурный синтез).

Первый камень в конструкцию учения о структуре заложили Г. Монж (1746-1818) и его ученики, разложившие машину на ее элементарные составляющие – механизмы, задачей которых являлось преобразование движений [12]. До этого считалось, что любую машину можно свести к «простым машинам» - рычагу, блоку, вороту, наклонной плоскости, клину, принцип работы которых основан на равновесии сил. Следующий шаг сделал А. Баумгартнер (1793-1855), который выделил последовательное и параллельное соединения механизмов. Немецкий машиновед Ф. Рело (1829-1905) создал учение о кинематических парах (подвижных соединениях звеньев). Он сделал вывод, что сущность механизма состоит не в физической весомости звеньев, а в связывающей их пустоте – паре. Рело ввел понятие кинематических цепей как совокупности звеньев и кинематических пар и представил механизм как частный случай кинематической цепи. Он положил начало структурному анализу, разложив механизм на звенья и пары, и структурному синтезу, показав, что механизм можно получить, закрепив одно из звеньев кинематической цепи. Ф. Грасгоф (1826-1893) при классификации кинематических пар использовал понятие степеней свободы. После опубликования его работы на повестку дня встал вопрос определения связи между числом степеней свободы механизма и числом звеньев и кинематических пар. Первым эту задачу решил П. Л. Чебышев (1821-1894), опубликовав в 1869 г. структурную формулу для плоских шарнирных механизмов с одной степенью свободы. Исследования в этом направлении продолжили М. Грюблер (1851-1935) и П.О. Сомов (1852-1919). Грюблер разработал ряд частных структурных формул для стержневых систем, в том числе для статически неопределимых механизмов и ферм, а Сомов предложил структурную формулу для кинематической цепи общего вида. Х.И. Гохман (1851-1916) нашел формулу, связывающую число замкнутых контуров механизма с числом образующих его звеньев и пар. Появление структурных формул расширило возможности структурного анализа и синтеза механизмов.

Структурная теория двигалась вслед за машиностроением, но никак не могла его догнать. Проектирование схемы механизма по заданным структурным свойствам с использованием структурных формул оказалось малоэффективным. Требовались новые, более мощные методы. Вплотную к решению этой задачи подошел Л. Бурместер (1840-1927), который использовал такие понятия, как элементарный механизм, состоящий из двух звеньев и одной пары, простой механизм, представляющий собой замкнутую кинематическую цепь, и составной механизм. Однако основоположником нового метода структурного синтеза механизмов стал Л.В. Ассур (1878-1920). До него были известны примеры построения механизмов путем присоединения к исходному механизму ферм, состоящих из двух звеньев и трех кинематических пар и даже фермы из четырех звеньев и шести пар. Ассур обобщил полученные индуктивным способом частные решения и сформулировал общий принцип образования плоских шарнирных механизмов, в соответствии с которым любой плоский шарнирный многозвенник можно получить путем последовательного наслоения на исходный элементарный механизм кинематических цепей нулевой подвижности (структурных групп). Он также разработал метод получения новых (ранее неизвестных) структурных групп. Первый этап развития структурной теории закончился в начале XX в. с появлением структурных классификаций механизмов по М. Грюблеру и Л. Ассуру. В основе классификации Грюблера лежала замкнутая кинематическая цепь, а у Ассура – структурная группа.

Отличительными чертами первого этапа развития структурной теории являются, с одной стороны, создание отдельных тематических компонент системы знаний о строении механизма: учений о кинематических парах и кинематических цепях, структурных формул, теории структурных групп, структурный анализ и структурный синтез, структурные классификации, а с другой,– отсутствие или слабая связь этих компонент между собой и с практикой проектирования.

Второй этап развития структурной теории (с середины 20-х до середины 60-х годов XXв.) характеризуется переосмыслением ранее полученных теоретических результатов с учетом нового фактического материала. А.П. Малышев (1879-1962) уточнил структурные формулы Чебышева и Сомова с учетом избыточных связей и произвольного числа степеней свободы. Он разделил кинематические пары на классы по числу условий связи, накладываемых на относительное движение звеньев. В.В. Добровольский (1880-1957) предложил различать кинематические пары по числу степеней свободы в относительном движении звеньев, выделив одноподвижные, двухподвижные и т.д. пары. Г.Г. Баранов (1899-1968) и В.В. Добровольский нашли новые способы получения структурных групп, а Г.Г. Баранов и И.И. Артоболевский (1905-1977) разработали их классификации. Накопившийся за годы исследований справочный материал по кинематическим и динамическим свойствам механизмов сделал возможным подбирать структурную схему механизма исходя не только из структурных, но и кинематических и динамических условий.

Главным достижением второго периода развития структурной теории стало создание И.И. Артоболевским и В.В. Добровольским учения о строении механизмов как системы, в которой отдельные тематические компоненты (теории кинематических пар и структурных групп, структурные анализ и синтез, структурная классификация) стали взаимосвязаны. Универсальная структурная классификация позволила связать между собой строение механизмов и методы их кинематического и силового анализа. Структурная теория стала каркасом новой науки и учебной дисциплины – теории механизмов, выделившейся из механики машин в конце 30-х гг. XX в.

На современном этапе развития структурной теории наряду с продолжением работ в традиционных разделах получили развитие новые направления. В связи с развитием вычислительной техники стало возможным на базе построения математических моделей структуры механизма проводить оценки функциональных возможностей сложных механизмов, что расширяет возможности структурного синтеза. В последние годы усилиями Л.Н. Решетова, О.Г. Озола, С.Н. Кожевникова (1906-1988) и их учеников интенсивно развивается новое направление в структурном синтезе механизмов – проектирование самоустанавливающихся (без избыточных связей) механизмов.

Понятие о структурном синтезе и анализе

Cтруктура любой технической системы определяется функционально связанной совокупностью элементов и отношений между ними. При этом для механизмов под элементами понимаются звенья, группы звеньев или типовые механизмы, а под отношениями подвижные (КП) или неподвижные соединения. Поэтому под структурой механизма понимается совокупность его элементов и отношений между ними, т.е. совокупность звеньев, групп или типовых механизмов и подвижных или неподвижных соединений. Геометрическая структура механизма полностью описывается заданием геометрической формы его элементов, их расположения, указания вида связей между ними. Структура механизма может быть на разных стадиях проектирования описываться различными средствами, с разным уровнем абстрагирования: на функциональном уровне - функциональная схема, на уровне звеньев и структурных групп - структурная схема и т.п. Структурная схема (рис.2.1) - графическое изображение механизма, выполненное с использованием условных обозначений рекомендованных ГОСТ (см. например ГОСТ 2.703-68) или принятых в специальной литературе, содержащее информацию о числе и расположении элементов (звеньев, групп), а также о виде и классе кинематических пар, соединяющих эти элементы. В отличие от кинематической схемы механизма, структурная схема не содержит информации о размерах звеньев и вычерчивается без соблюдения масштабов.

Любой механизм является трехмерным объектом, поэтому для описания его строения используют трехмерные (пространственные) структурные модели. Для описания строения плоских механизмов используют также двумерные (плоские) структурные модели, представляющие собой проекцию трехмерных на плоскость.

Кинематическая схема механизма – структурная схема механизма с указанием размеров звеньев, необходимых для кинематического анализа механизма.

Стойка на структурной схеме отмечается штриховкой; все звенья нумеруются; кинематические пары обозначаются латинскими буквами. Звено, входящее в одну или две низшие пары, изображается в виде стержня, а звенья, входящие в три и более кинематические пары, могут изображаться также в виде треугольника, четырехугольника и т.д. и заштриховываться. Если на схеме несколько звеньев соединяются одним шарниром, то это многократный шарнир и число кинематических пар в нем на единицу меньше числа сходящихся звеньев. Следует отметить, что треугольник, образованный тремя звеньями и тремя кинематическими парами, является одним звеном, так как образовавшие его стержни не имеют относительного движения. Поэтому в структурной схеме такой жесткий треугольник часто заштриховывается (рис.2.1). Для звеньев, образующих высшую кинематическую пару, показываются элементы кинематических пар. Структурная схема механизма может быть представлена и аналитической записью.

Рис.2.1. Структурная схема механизма

Как на любом этапе проектирования при структурном синтезе различают задачи синтеза и задачи анализа.

Задачей структурного анализа является задача определения параметров структуры заданного механизма - числа звеньев и структурных групп, числа и вида КП, числа подвижностей (основных и местных), числа контуров и числа избыточных связей.

Задачей структурного синтеза является задача синтеза структуры нового механизма, обладающего заданными свойствами: числом подвижностей, отсутствием местных подвижностей и избыточных связей, минимумом числа звеньев, с парами определенного вида (например, только вращательными, как наиболее технологичными) и т.п.

Основные понятия структурного синтеза и анализа

Подвижность механизма - число независимых обобщенных координат однозначно определяющее положение звеньев механизма на плоскости или в пространстве.

Связь - ограничение, наложенное на перемещение тела по данной координате.

Избыточные (пассивные) - такие связи в механизме, которые повторяют или дублируют связи, уже имеющиеся по данной координате, и поэтому не изменяющие реальной подвижности механизма. При этом расчетная подвижность механизма уменьшается, а степень его статической неопределимости увеличивается. Иногда используется иное определение: Избыточные связи - это связи число которых в механизме определяется разностью между суммарным числом связей, наложенных кинематическими парами, и суммой степеней подвижности всех звеньев, местных подвижностей и заданной (требуемой) подвижностью механизма в целом.

Местные подвижности - подвижности механизма, которые не оказывают влияния на его функцию положения (и передаточные функции), а введены в механизм с другими целями (например, подвижность ролика в кулачковом механизме обеспечивает замену в высшей паре трения скольжения трением качения).

Свойства связей

В классической механике связями называют ограничения, налагаемые на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах. Они могут быть записаны в виде уравнений или неравенств. Уравнения, которым в силу наложенных связей должны удовлетворять координаты точек механической системы и их скорости (первые производные от координат по времени), называются уравнениями связей. Самыми распространенными в механизмах являются геометрические связи, которые ограничивают относительные перемещения звеньев и уравнения которых содержат только координаты точек (и, может быть, время). Такие связи имеют все кинематические пары и кинематические соединения с твердыми промежуточными элементами.

Кроме геометрических связей, в механизмах могут быть дифференциальные (кинематические) связи, уравнения которых содержат координаты точек и производные от этих координат по времени (и, может быть, время). Если эти уравнения интегрируются, то дифференциальная связь приводится к геометрической. Дифференциальные интегрируемые и геометрические связи называются голономными связями. Дифференциальные связи, уравнения которых не могут быть проинтегрированы, являются неголономными связями. Неголономные связи появляются в кинематических парах при учете трения.

Особое место занимает фрикционная пара. Рассмотрим фрикционную передачу (рис.2.1.1), состоящую из цилиндрических катков 1 и 2, стержня 3, стойки 5 и пружины 4, которая не входит в число звеньев и предназначена для обеспечения необходимого прижатия катков.

Рис.2.1.1

Выясним, какие связи накладывает высшая кинематическая пара В, которая образуется в месте соприкосновения катков. Цилиндрические колеса соприкасаются по общей образующей, совпадающей с осью Х, проходящей перпендикулярно плоскости чертежа. Кинематическая пара ликвидирует перемещение вдоль оси У и вращение вокруг оси Z, накладывая две геометрические связи. Если трение между катками настолько велико, что нет проскальзывания, то наложена еще одна (дифференциальная) связь. Уравнение этой связи следует из кинематического условия Vв = ω₁r₁ = ω₂r₂.

Интегрируя и принимая, что в начале φ₁ = 0 и φ₂ = 0, получаем φ₂ = φ₁r₁/r₂. Полученное уравнение связи выражает зависимость между угловыми перемещениями колес и имеет вид геометрической связи. Известно, что передача движения во фрикционной передаче обусловлена упругим скольжением деформированных участков катков, поэтому приведенное уравнение связи можно рассматривать только как первое приближение к действительному. С учетом упругого скольжения φ₂ = φ₁r₁ (1-λ)/r₂, где λ – коэффициент скольжения, зависящий от силы прижатия катков, материала катков и вида смазочного материала. Во втором приближении коэффициент скольжения λ считается постоянным (определяется опытным путем). Второе приближение оказывается достаточно точным в инженерных расчетах при оценке сил и прочности в передаче ('' Детали машин ''). Ввиду малости коэффициента λ (0,03…0,001) для кинематического анализа обычно достаточно и первого приближения. Связь, обусловленную трением между катками во фрикционной передаче, называют псевдокинематической.

Кроме голономной или неголономной связь может быть удерживающей или неудерживающей, стационарной или нестационарной. Связи, в уравнения которых время явно не входит, называют стационарными. В уравнение нестационарной связи время входит в явной форме. Удерживающими называют связи, при наличии которых для любого возможного перемещения точки механической системы противоположное ему перемещение также является возможным. Удерживающие связи описываются равенствами, а неудерживающие - неравенствами. Неудерживающие связи характерны для гибких звеньев.

В курсе «Теория механизмов» рассматриваются механизмы с голономными, стационарными и удерживающими связями. В механизмах связи обычно действуют постоянно. Однако существуют механизмы переменной структуры, в которых связи, оставаясь стационарными, изменяются в какой-то момент времени. Например, в планетарной коробке скоростей из одного зубчатого механизма с несколькими степенями свободы путем включения элементов управления (муфт и тормозов) получают несколько различных по строению механизмов с одной степенью свободы. Другим примером механизма переменной структуры может служить фрикционный механизм (рис.2.1.1), в котором при недостаточной силе прижатия катков начинается буксование: входное звено вращается, а выходное - неподвижно.

Степень свободы и классы кинематических пар

Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой.

Совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару, называется элементом кинематической пары.

Если звенья подвижно соединяются в нескольких местах, то кинематическая пара является разветвленной, а отдельные части этого соединения называются ветвями кинематической пары.

Любой механизм состоит из звеньев, соединенных между собой кинематическими парами. Возможные подвижные соединения звеньев весьма разнообразны. Например, на рис.2.1.2,а показана так называемая вращательная кинематическая пара, в которой соединение звеньев А и В образуется двумя цилиндрами, находящимися в постоянном соприкосновении.

На рис.2.1.2,б изображен другой способ соединения двух звеньев А и В. Эта пара допускает относительное перекатывание, скольжение или верчение.

а) б)

Рис.2.1.2

Таким образом, на относительное движение каждого звена кинематической парой накладываются ограничения, зависящие от способа соединения звеньев в пары. Эти ограничения называются числом условий связи S. Рассмотрим теперь, какие же связи и в каком количестве могут быть наложены на относительное движение звеньев кинематической парой.

Для абсолютно твердого тела, свободно движущегося в пространстве пространстве (в декартовой системе координат X, Y, Z), число независимых параметров, определяющих его положение в пространстве или число степеней свободы, равно шести (рис.2.2): три возможных перемещения вдоль неподвижных координатных осей X, Y и Z и три возможных вращения вокруг этих осей.

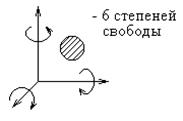
Рис. 2.2. Степени свободы тела в пространстве

Для звеньев, вошедших в кинематическую пару, число степеней свободы всегда меньше шести, так как кинематическая пара уменьшает число возможных перемещений и накладывает число условий связи S на относительное движение каждого звена, зависящих от способа соединения звеньев в пары. В таком случае число степеней свободы H кинематической пары равно

H = 6 − S. (1)

Все кинематические пары делятся на классы в зависимости от числа условий связи, налагаемых ими на относительное движение звеньев. Так как число условий связи может быть от одного до пяти, то число классов пар равно пяти. В соответствии с этим имеем кинематические пары I −V классов. Например, если телами (звеньями), образовавшими кинематическую пару, утрачено по 5 степеней свободы каждым, эту пару называют кинематической парой 5-го класса. Если утрачено 4 степени свободы – 4-го класса и т.д. (рис.2.3). При S=0 пары не существует, а есть два тела, движущихся независимо друг от друга. При S=6 кинематическая пара становится жестким соединением двух звеньев, т.е. одним звеном.

Класс кинематической пары может быть определен из зависимости (1):

S = 6 – H. (2)

На рис. 2.3 представлены кинематические пары различных классов.

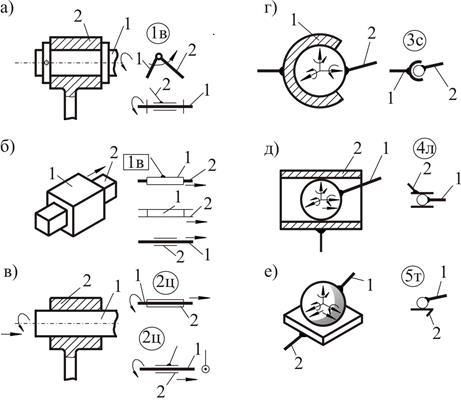
Рис.2.3

Одноподвижные кинематические пары V класса (Н=1, S=5) могут быть двух видов: одноподвижная вращательная пара (условное обозначение , рис. 2.3,а) допускает лишь одно относительное вращательное движение звеньев вокруг оси (показано стрелкой); звенья 1 и 2 соприкасаются по цилиндрической поверхности; следовательно, это низшая пара, замкнута геометрически. Роль такой кинематической пары выполняет более сложная конструкция - шарикоподшипник.

Одноподвижная поступательная кинематическая пара V класса (условное обозначение , рис. 2.3,б) с геометрическим замыканием, низшая, допускает лишь одно прямолинейное поступательное относительное движение звеньев.

Двухподвижная цилиндрическая кинематическая пара IV класса (Н=2, S=4, условное обозначение , рис. 2.3,в) с геометрическим замыканием, низшая, допускает независимые относительные движения звеньев – вращательное вокруг оси и поступательное вдоль оси кинематической пары.

Трехподвижная сферическая кинематическая пара III класса (Н=3, S=3, условное обозначение , рис. 2.3,г) с геометрическим замыканием, низшая, допускает три независимых относительных вращения звеньев вокруг осей x, y, z.

Четырехподвижная линейная кинематическая пара II класса (Н=4, S=2) и пятиподвижная точечная кинематическая пара I класса (Н=5, S=1) и их условные обозначения ( и , даны на рис. 2.3,д,е). Возможные независимые относительные движения звеньев (вращательные и поступательные) показаны стрелками. Это высшие пары, поскольку контакт элементов звеньев линейный (шар в цилиндре) и точечный (шар на плоскости). Пара – с геометрическим замыканием, а пара требует силового замыкания.

Таблица 1. Возможные комбинации независимых вращательных (В)

и поступательных (П) движений в кинематических парах

Кинематические пары	Возможные движения
Одноподвижные	В П
Двухподвижные	ВВ ВП
Трехподвижные	ВВВ ВВП ВПП
Четырехподвижные	ВВВП ВВПП
Пятиподвижные	ВВВПП

Пример 1.

Рис.2.4. Пятиподвижная кинематическая пара

Число степеней свободы звеньев данной кинематической пары (рис.2.4) H = 5. Действительно, движение шара вдоль оси z ограничено плоскостью, а в сторону, обратную плоскости, невозможно, так как нарушило бы соприкосновение звеньев. Таким образом, движение шара может быть представлено как вращение вокруг трех осей и движение вдоль двух осей: число простейших движений шара равно пяти. Следовательно, число степеней свободы звеньев данной кинематической цепи H=5. Тогда число условий связи равно

S = 6 – H = 6 – 5=1.

Поэтому пара, изображенная на рис. 2.4, относится к парам I класса (пятиподвижная пара).

Для решения вопроса, к какому классу относится та или иная кинематическая пара, целесообразно использовать следующий метод.

Одно из звеньев, входящих в кинематическую пару, представить неподвижным. Связать с ним систему координат Oxyz и, ориентируясь по ней, проследить, какие движения другого звена пары невозможны из шести движений, которые оно имело бы возможность совершать, не входя в пару. Число этих невозможных движений (как равное числу связей в паре) представит собой номер класса пары.

Пример 2.

Рис.2.5. Четырехподвижная кинематическая пара

Свяжем систему координат Oxyz с плоскостью. Рассмотрим цилиндр. Находясь в кинематической паре с плоскостью, он лишен возможности совершать поступательное движение вдоль оси Oz, а также вращательное движение вокруг оси Oy Таким образом, число условий связи равно двум.

Поэтому данная кинематическая пара относится к парам II класса (четырехподвижная пара).

Пример 3.

Рассмотрим кинематическую пару «винт-гайка» (рис.2.4). Число степеней подвижности этой пары H равно 1, а число налагаемых связей S равно 5. Это пара будет являться парой пятого класса, свободным можно выбрать только один вид движения для винта или гайки, а второе движение будет сопутствующим.

Рис.2.6

Таким образом, существует следующее соответствие между классом кинематической пары и числом степеней свободы ее звеньев:

Кинематическая пара I класса – пятиподвижная пара;

кинематическая пара II класса – четырехподвижная пара;

кинематическая пара III класса – трехподвижная пара;

кинематическая пара IV класса – двухподвижная пара;

кинематическая пара V класса – одноподвижная пара.

Классификация кинематических пар

Кинематические пары (КП) классифицируются по следующим признакам:

1) по виду места контакта (места связи) поверхностей звеньев:

- низшие, в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения). К низшим парам относятся: вращательная, поступательная, винтовая, цилиндрическая, сферическая, плоскостная и т.п. (Пример низшей кинематической пары: два цилиндра, находящиеся в постоянном соприкосновении, из которых один вращается внутри другого).

- высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием). Они имеются, например, в зубчатых и кулачковых механизмах. При этом линейный или точечный контакт понимается как первоначальный - при соприкосновении звеньев без усилия, а под нагрузкой звенья, образующие высшую пару, будут соприкасаться по некоторой фактической поверхности, называемой пятном контакта.

Преимуществом низших кинематических пар по сравнению с высшими является возможность передачи больших нагрузок, поскольку контактная поверхность соприкасающихся звеньев низшей пары может быть весьма значительной, имеют большие потери на трение, сложнее синтезируются. Имеют простые формы в виде плоскостей, цилиндрических поверхностей, поэтому более технологичны, т. е. просты в изготовлении.

Применение высших пар позволяет передавать меньшие нагрузки, легко проектируются, а также позволяют уменьшить трение в машинах (пример – шариковый или роликовый подшипник), а также получить самые различные законы движения выходного звена механизма путем придания определенной формы звеньям, образующим высшую пару. Элементы этих пар сложны в изготовлении.

2) по относительному движению звеньев, образующих пару:

- вращательные;

- поступательные;

- цилиндрические;

- сферические;

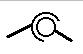
- винтовые;

- плоские.

Механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары, называют рычажным.

3) по способу замыкания (обеспечения контакта звеньев пары):

Для того чтобы элементы кинематических пар находились в постоянном соприкосновении, они должны быть замкнуты. Замыкание бывает:

- силовое (за счет действия сил тяжести, силы упругости пружины, инерции, давления жидкости и газа, рис.2.7);

- геометрическое (за счет конструкции рабочих поверхностей пары, рис.2.8).

Низшие кинематические пары (вращательная, поступательная, винтовая, цилиндрическая, плоскостная и сферическая ) выполняются, как правило, с геометрическим замыканием, а высшие – с силовым.

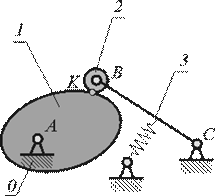
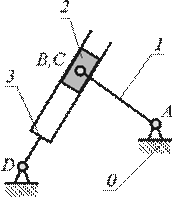
Рис.2.7 Рис.2.8

4) по числу подвижностей в относительном движении звеньев.

5) по числу условий связи, накладываемых на относительное движение звеньев (число условий связи определяет класс кинематической пары).

Таблица 2. Условные обозначения кинематических пар

Класс пары	Число условий связи	Число степеней свободы	Название пары	Рисунок	Условное обозначение
I	1	5	Шар-плоскость
II	2	4	Шар-цилиндр
III	3	3	Сферическая
III	3	3	Плоскостная
IV	4	2	Цилиндрическая
IV	4	2	Сферическая с пальцем
V	5	1	Поступательная
V	5	1	Вращательная
V	5	1	Винтовая

Классификация кинематических цепей

Кинематической цепью называется система звеньев, связанных между собой кинематическими парами.

Кинематические цепи бывают:

- замкнутые (простые).

Простой кинематической цепью называется такая, у которой каждое звено входит не более чем в две кинематические пары.

Замкнутой кинематической цепью называется кинематическая цепь, звенья которой образуют один или несколько замкнутых контуров.

- незамкнутые (простые).

Незамкнутой кинематической цепью называют такую, в которой имеются звенья, входящие только в одну кинематическую пару. Простейшая незамкнутая цепь является двухзвенной.

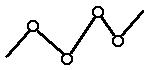
- сложные. Сложной кинематической цепью называется цепь, в которой имеется хотя бы одно звено, входящее более чем в две кинематические пары.

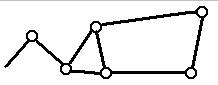
По признаку наличия разветвлений различают цепи простые (каждое звено цепи входит не более, чем две кинематических пары) и сложные или разветвленные (некоторые звенья входят в три, или более пары); в разветвленных цепях могут присутствовать так называемые кратные (двойные, тройные и т.д.) шарниры.

По области движения звеньев цепи бывают плоские и пространственные. В пространственных кинематических цепях траектории точек звеньев являются пространственными кривыми или плоскими, но расположенными в непараллельных плоскостях. В плоских цепях точки звеньев описывают траектории, лежащие в параллельных плоскостях.

Механизм − это кинематическая цепь, в которой при заданном движении одного или нескольких звеньев относительно одного из них все остальные звенья совершают однозначно определяемые движения.

Ведущим звеном называется звено, для которого сумма элементарных работ внешних сил, приложенных к нему, является положительной. Ведомым звеном называется звено, для которого сумма элементарных работ всех внешних сил, приложенных к нему, является отрицательной или равна нулю.

Входное звено может быть как ведущим, так и ведомым. То же относится и к ведомому звену.

В зависимости от вида кинематической цепи механизмы делятся на плоские и пространственные.

Чтобы изучить движение механизма, недостаточно знать его структуру, необходимо также знать размеры отдельных звеньев, взаимное положение звеньев. Поэтому при изучении движения звеньев механизма обычно составляют так называемую кинематическую схему механизма. Кинематическая схема механизма строится в выбранном масштабе с точным соблюдением всех размеров и форм.

Чтобы из кинематической цепи получить механизм, необходимо:

- одно звено сделать неподвижным, т.е. образовать станину (стойку);

- одному или нескольким звеньям задать закон движения (сделать ведущими) таким образом, чтобы все остальные звенья совершали требуемые целесообразные движения.

Степень свободы и структурная формула механизма

Число степеней свободы механизма – это число степеней свободы всей кинематической цепи относительно неподвижного звена (стойки).

Если на движение звена в пространстве не наложено никаких условий связи, то оно обладает шестью степенями свободы. Тогда если число звеньев кинематической цепи равно к, то общее число степеней свободы, которым обладают к звеньев до их соединения в кинематические пары, равно 6к. Соединение звеньев в кинематические пары накладывает различное число условий связи S на относительное движение звеньев, зависящее от класса пар.

Если число пар I класса, у которого S₁=1, а H₁=5, в которые входят звенья рассматриваемой кинематической цепи, равно р₁, число пар II класса, у которого S₁=2, а H₁=4 – р₂, число пар III класса, у которого S₁=3, а H₁=3 – р₃, число пар IV класса, у которого S₁=4, а H₁=2 – р₄, число пар V класса, у которого S₁=5, а H₁=1 – р₅, то из 6к степеней свободы, которыми обладали звенья до вхождения в кинематические пары, необходимо исключить те степени свободы, которые отнимаются вхождением звеньев в кинематические пары (одна пара V класса (одноподвижная) лишит кинематическую цепь пяти степеней свободы; p₅ таких пар лишит данную кинематическую цепь 5p₅ степеней свободы. Все пары IV класса отнимут у кинематической цепи 4p₄ степеней свободы и т. д.). Тогда число степеней свободы Н кинематической цепи равно

Н = 6к - 5р₅ - 4р₄ - 3р₃ - 2р₂ – р₁. (3)

Формула (3) − это формула подвижности или структурная формула кинематической цепи общего вида. Данная формула называется формула Малышева, получена П.И. Сомовым в 1887 году и развита А.П. Малышевым в 1923 году.

При изучении движения механизма рассматриваем абсолютные перемещения, происходящие относительно одного из звеньев, принятого за неподвижное (стойку). Так как одно звено неподвижно, то число степеней свободы цепи уменьшится на шесть и число степеней свободы W механизма относительно неподвижного звена будет равно

W = H – 6 или W = 6(к-1) - 5p₅ - 4p₄ - 3p₃ - 2p₂ – p₁

или

W = 6n -5p₅ - 4p₄ - 3p₃ - 2p₂ – p₁, (4)

где n=k-1 − число подвижных звеньев кинематической цепи. Формула (4) носит название формулы подвижности, или структурной формулы механизма общего вида.

Величина W показывает, сколько должно быть у механизма ведущих звеньев (если W = 1 – одно, W = 2 – два ведущих звена и т.д.).

Если механизм обладает одной степенью свободы, то одному из звеньев механизма можем предписать относительно стойки какой-либо определенный закон движения (одну обобщенную координату механизма), например вращательное, поступательное или винтовое движение с заданными скоростями. При этом все остальные звенья механизма получат вполне определенные движения, являющиеся функциями заданного. Если механизм обладает двумя степенями свободы, то необходимо задать одному из звеньев два независимых движения (две обобщенные координаты механизма) относительно стойки или двум звеньям по одному независимому движению относительно стойки.

Обобщенными координатами механизма называют независимые между собой координаты, однозначно определяющие положение всех звеньев механизма относительно стойки. Например, в кривошипно-ползунном механизме за обобщенную координату можно принять угол поворота кривошипа α₁, так как положение звена 1, определяемое этим углом, определяет также положение всех других подвижных звеньев. Звено, которому приписывается одна или несколько обобщенных координат, называется начальным. Начальное звено не всегда совпадает с входным звеном.

Для определения числа степеней свободы механизма достаточно найти общее число координат, определяющих положение всех звеньев механизма, и число уравнений, связывающих эти координаты.

Рис.2.9. Шарнирный параллелограмм с избыточной связью (а), шарнирный четырехзвенник без избыточной связи и его

крайнее положение (б)

Дополнительные требования существенно изменяют характер движения механизма и соответственно вид структурной формулы. Пусть, например, у механизма (рис.2.9), который состоит из кинематических пар пятого класса р₅ = 4 (А,В,С,D), оси всех пар параллельны. Выберем неподвижную систему координат xyz так, чтобы ось x совпала с направлением осей пар, в результате получим плоский механизм, т.е. механизм, точки звеньев которого описывают траектории, лежащие в параллельных плоскостях. В таком случае звенья механизмов не могут совершать вращательное движение вокруг осей y и z и поступательное движение вдоль оси х, т.е. из шести возможных движений три не могут быть осуществлены. Так как три связи уже наложены условием параллельности осей, структурная формула будет такой:

W = (6-3)n - (5-3)p₅ - (4-3)p₄ - (3-3)p₃,

или

W = 3n - 2p₅ – p₄. (5)

Формула (5) есть структурная формула для плоских механизмов общего вида. Формулу (5) называют также формулой П.Л. Чебышева (1869). Она может быть получена из формулы Малышева при условии, что на плоскости тело обладает не шестью, а тремя степенями свободы.

В состав плоских механизмов пары I, II и III классов входить не могут, как обладающие пространственным характером возможных относительных движений. Из рассмотренного примера следует, что если на движение всех звеньев механизма в целом наложено некоторое общее для всего механизма число связей, то необходимо число этих общих связей из структурной формулы механизма (4) исключить путем вычитания числа этих связей из числа степеней свободы всех подвижных звеньев механизма и из числа условий связи всех входящих в механизм кинематических пар. По наличию общих условий связи определяется семейство механизмов.

При расчете степени подвижности механизма по формуле (5) необходимо учитывать следующие, нередко встречающиеся ситуации:

1) наличие кратных шарниров; так, соединение звеньев, показанное на рис. 2.10, необходимо считать как два шарнира, иначе расчет по (5) даст завышенное значение W;

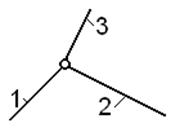
Рис.2.10. Двойной шарнир

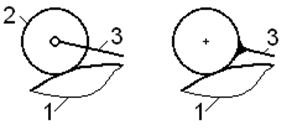
2) наличие местных подвижностей, т.е. таких, устранение которых не повлияет на кинематику механизма; у механизма по рис. 2.11 при любом положении кулачка 1 коромысло 3 может занимать только одно (единственно возможное) положение; следовательно, у этого механизма заведомо W=1, однако расчет по формуле (1) приводит к явно завышенному значению

W= 3∙3 – 1 - 2∙3 = 2;

для получения достоверного результата нужно ролик 2 мысленно объединить с коромыслом 3 в одно звено (рис. 2.11, б), тогда фактическая подвижность механизма

W= 3∙2 – 1 - 2∙2 = 1.

.

а) б)

Рис.2.11. Устранение местной подвижности

Отметим, что эти действия корректны только при круглом ролике, у которого геометрический центр совпадает с центром шарнира;

3) наличие пассивных (или избыточных) связей.

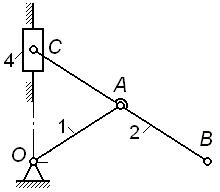
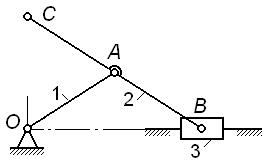
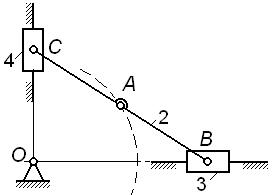
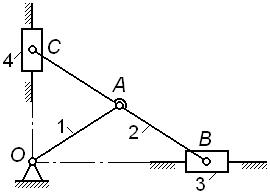
На рис. 2.12, а – г показаны четыре варианта исполнения механизма эллипсографа (длины звеньев OA=AB=AC).

Анализ кинематических свойств этих схем показывает следующее:

- у механизма по рис. 2.12, а подвижность W=1, траектория точки B – горизонтальная прямая; следовательно, без ущерба для подвижности и кинематики механизма допускается включение в его схему ползуна 3 (как в схеме по рис. 2.12, г);

- аналогично у механизма по рис. 2.12, б также W=1, а траектория точки C – вертикальная прямая и его схему можно заменить той же схемой 2.12, г постановкой ползуна 4;

- у механизма по рис. 2.12, в степень подвижности W=1 и траектория точки A – окружность радиуса OA; следовательно, без ущерба для подвижности и кинематики механизма в его схему можно включить кривошип 1 длиной OA=AB=AC, как в схеме по рис. 2.12, г.

Подытоживая, заключаем, что механизм по рис. 2.12, г кинематически эквивалентен любому из трех остальных механизмов; однако расчет по формуле (5) приводит к заведомо заниженному результату

W = 3∙4 – 0 - 2∙6 = 0,

т.е. формально – это не механизм, а ферма, что противоречит фактам. В таких случаях говорят, что механизм имеет избыточные или пассивные связи, которые, хотя и присутствуют в механизме, не влияют на его кинематику.

а) б)

в) г)

Рис.2.12

От пассивных связей при структурном анализе механизмов следует избавляться: в данном случае, в зависимости от смысла решаемой задачи, цель достигается удалением одного из звеньев – 1, 3 или 4 (вместе с соответствующим кинематическими парами). Тогда

W= 3∙3 – 0 - 2∙4 = 1,

что соответствует истине.

Лишние степени свободы

Необходимо отметить, что, кроме степеней свободы и связей, активно воздействующих на характер движения механизмов, в них могут встретиться степени свободы и условия связи, не оказывающие никакого влияния на характер движения механизма в целом или повторяют ограничения наложенные другими связями. Такие степени свободы называются лишними степенями свободы, или соответственно местными или групповыми подвижностями, а связи – избыточными или пассивными.

Местные подвижности бывают полезными или вредными для работы механизма. Их часто специально вводят в механизм для уменьшения износа элементов пары, улучшения условий смазки, самоустановки звеньев под нагрузкой, повышения надежности и КПД. Например, применение ролика 2 (рис.2.12.1) позволяет заменить трение скольжения между кулачком 1 и коромыслом 3 на трение качения, уменьшая при этом износ.

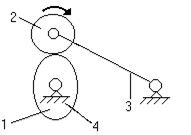
Рис.2.12.1. Схема механизма с местной подвижностью

В тоже время лишние степени свободы могут приводить к возникновению дополнительных вибраций и инерционных сил. Вращение шатуна 2 вокруг своей оси в четырехзвеннике (рис.2.12.2) может оказаться полезной или вредной лишней степенью свободы, что может быть установлено только при специальном исследовании.

Рис.2.12.2. Схема механизма с местной подвижностью

Если местная подвижность часто оказывается полезной, то групповая подвижность в большинстве случаев недопустима, например, в четырехзвеннике (рис.2.12.3) шатун 2 и коромысло 3 имеют возможность поворота вокруг оси, проходящей через шарниры В и D, что может привести к заклиниванию механизма.

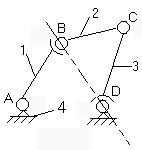
Рис.2.12.3. Схема механизма с групповой подвижностью

В то же время у манипуляторов промышленных роботов подвижность группы звеньев позволяет обеспечить необходимую маневренность. Маневренность манипулятора – способность манипулятора обходить препятствия в рабочем пространстве. Она дает возможность некоторым звеньям манипулятора располагаться в более удобной позиции при одном и том же положении захвата.

В некоторых механизмах встречается мгновенная подвижность, под которой понимается степень свободы механизма, существующая только в определенных его положениях. Например, в механизме шарнирного параллелограмма (рис.2.12.4) AB=DC и BC=AD, поэтому угловые скорости входного 1 и выходного 3 звеньев совпадают.

Рис.2.12.4. Схема механизма с мгновенной подвижностью

В положении, когда все звенья располагаются на одной линии (показано штриховой линией), появляется еще одна степень свободы – возможность поворота точки вокруг шарниров и D при неподвижном звене 1. Мгновенная подвижность появилась вследствие того, что в данном положении механизма две разные связи стали тождественными, то есть появилась мгновенная избыточная связь (рис.2.12.5).

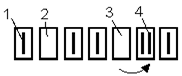
Рис. 2.12.5. Схема образования мгновенной подвижности

в механизме с одной степенью свободы: 1- связь;

2 – степень свободы; 3 – мгновенная степень свободы;

4 – мгновенная избыточная связь

Для устранения мгновенной подвижности, которая создает неопределенность движения (точка может поворачиваться вокруг шарниров как по, так и против часовой стрелки), применяют разные методы, в том числе и постановку дополнительного пассивного звена.

При анализе колебаний в механизмах с упругими звеньями и промежуточными элементами (виброизоляторами, пружинами), кроме рассмотренных структурных степеней свободы, обусловленных геометрическими связями, вводят параметрические степени свободы, зависящие от конструктивных (масса, жесткость) параметров звеньев и режима движения механизма.

Рассмотрим кулачковый механизм с роликовым толкателем (рис.2.12.6). Между кулачком 1 и толкателем 2 кулачкового механизма устанавливается ролик 3 для устранения трения.

Рис. 2.12.6. Кулачковый механизм

с роликовым толкателем

В этом случае степень подвижности механизма, вычисленная по формуле П.Л. Чебышева, будет равна 2:

W = 3n – 2p₅ - p₄= 3∙3 - 2∙3 – 1 = 2.

Здесь явно присутствует лишняя степень свободы, а именно вращение ролика под действием силы трения качения. Её следует учитывать при проведении структурного анализа данного механизма. Ведь очевидно, что данный механизм может функционировать и без ролика 3. Но при этом трение качения будет заменено трением скольжения между кулачком и толкателем (высшей кинематической парой), что увеличивает потери мощности в механизме на преодоление сил трения.

Тогда степень свободы такого механизма вычисляется по формуле

W = 3n – 2p₅ - p₄ - q,

где q – количество лишних степеней свободы.

Избыточные связи

Избыточные (повторяющиеся) связи имеют следующие свойства:

-устранение избыточных связей не влияет на кинематику механизма;

-каждая избыточная связь увеличивает статическую неопределимость механизма на единицу.

Различают три типа избыточных связей.

1. Избыточные связи на элементах кинематических пар. В трехподвижной плоскостной паре требуемое относительное движение может быть получено постоянным соприкосновением ее элементов по поверхности. Эта кинематическая пара накладывает на относительное движение звеньев три геометрические связи и позволяет передавать силу вдоль оси перпендикулярной плоскости соприкосновения и две пары сил вокруг осей, лежащих в этой плоскости. Однако для реализации этой функции достаточно было бы соприкосновения обоих звеньев только в трех точках. Соприкосновение во всех остальных точках создает в неограниченном количестве избыточные связи. В результате этого реакции связей становятся статически неопределимыми, и для их расчета необходимо применять гипотезы о распределении напряжений по площадке контакта. Поступая аналогично, в любой кинематической паре соприкосновение по поверхностям и линиям можно заменить соприкосновением в точках, число которых равно классу пары (S).

Эти избыточные связи желательны, так как они снижают контактные давления, увеличивают допустимую нагрузку на подвижные соединения и уменьшают износ. Число таких связей увеличивают с помощью ручной обработки (шабровки), на металлорежущих станках и в процессе приработки легко нагруженного механизма в условиях хорошей смазки (обкатка механизма).

2. Избыточные связи в разветвленных подвижных соединениях. В механизмах часто встречаются разветвленные подвижные соединения двух звеньев, состоящие из отдельных частичных соединений (ветвей), например, вал и стойка (рис.2.12.7,а) образуют вращательную кинематическую пару А, имеющую две ветви А₁ и А₂.

Рис.2.12.7

Каждое из частичных соединений накладывает на относительное движение вала по 5 связей, допускающих только вращение вала вокруг своей оси. При абсолютно точном изготовлении жестких вала и опор уравнения связей в ветвях А₁ и А₂ тождественны. Так как для реализации требуемого вращательного движения вала достаточно 5 связей, то остальные 5 являются повторяющимися, причем нельзя указать, связи какой ветви А₂ или А₁ являются основными, а какой избыточными. При неточном изготовлении опор (рис. 2.12.7,б) избыточные связи превращаются в дополнительные к имеющимся ограничения на относительное движение вала. Уравнения связей в ветвях А₁ и А₂ уже не тождественны, сборка такой кинематической пары возможна только за счет деформации вала, а подвижное соединение из–за заклинивания вала в опорах может превратиться в неподвижное. Если вал установить на опоры в виде сферических подшипников, из которых один (А₂) плавающий, а второй (А₁) неподвижен в осевом направлении (рис.2.1.7,в), то число избыточных связей будет равно нулю, а система станет статически определимой и нечувствительной к неточностям изготовления и монтажа. Задача выбора подвижных соединений при установке вала редуктора на опоры конструктивно решается в деталях машин.

Главным показателем качества конструкции разветвленного соединения является число избыточных связей. Чем больше этих связей в соединении, тем точнее его надо изготовить, тем чувствительнее соединение к деформациям и самозаклиниванию, тем труднее его монтаж и демонтаж. Тем не менее, в случаях, когда удается обеспечить при изготовлении и сборке требуемую точность разветвленных соединений, они широко применяются на практике, так как повышают жесткость и прочность подвижных соединений, например, в зубчатой передаче стремятся увеличить число пар зубьев, одновременно находящихся в зацеплении, уменьшая тем самым нагрузку, приходящуюся на один зуб; шлицевое (зубчатое) соединение используют в качестве поступательной кинематической пары; в подшипнике качения размещают большое число шариков или роликов между наружным и внутренним кольцами.

3. Контурные избыточные связи. Избыточные связи этого типа образуются в замкнутых контурах кинематических цепей. В незамкнутых кинематических цепях контурные избыточные связи отсутствуют. Если говорят о необходимости устранения избыточных связей, то обычно имеют в виду контурные связи. Эти связи родственны избыточным связям второго типа, но их труднее обнаружить и от них в большей степени зависят эксплуатационные свойства и технологичность механизма. В механизме двойного параллелограмма (рис.2.12.8) для основного четырехзвенного механизма ACDF выполняется условие AC=DF и CD=AF, т.е. ACDF – параллелограмм. Постановка дополнительного звена BE=CD при условии AB=FE вносит в механизм избыточную геометрическую связь, тождественную внесенной ранее звеном CD. Если точность выполнения указанных геометрических соотношений окажется недостаточной, то сборка и последующее движение механизма будут сопровождаться деформациями (натягами) звеньев.

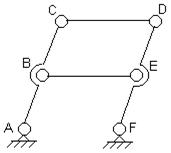
Рис.2.12.8

Вследствие нагрузки и температуры в механизмах с избыточными связями возникают дополнительные напряжения, которые увеличивают износ и снижают КПД. Изготовление таких механизмов дороже, затруднен их монтаж и демонтаж, существует угроза заклинивания и поломок. Распределение давлений на элементах кинематических пар неравномерно, поэтому необходима длительная обкатка механизма.

Если избыточные связи отсутствуют, то сборка механизма происходит без деформирования звеньев, последние как бы самоустанавливаются; поэтому такие механизмы называют самоустанавливающимися или оптимальными. Механизмы с избыточными связями (q>1) нельзя собрать без деформации звеньев. Такие механизмы требуют повышенной точности изготовления, в противном случае в процессе сборки звенья деформируются, трение в кинематических парах может сильно увеличиться и привести к заклиниванию звеньев. Поэтому с этой точки зрения избыточные связи в механизме нежелательны.

Однако в целом ряде случаев приходится сознательно проектировать и изготавливать статически неопределимые механизмы с избыточными связями для обеспечения нужной прочности и жесткости системы, особенно при передаче больших сил.

Таким образом, на практике при конструировании машин не следует стремиться устранять или же оставлять минимальное количество избыточных связей, т.к. это может оказаться невыгодным из-за усложнения конструкции или по каким-либо другим соображениям. В общем случае оптимальное решение следует искать, учитывая наличие необходимого технологического оборудования, стоимость изготовления, требуемые ресурс работы и надежность машины, следовательно, это весьма сложная задача на оптимизацию для каждого конкретного случая.

Методику определения и устранения избыточных связей в кинематических цепях механизмов рассмотрим на примерах.

На рис. 2.9,а показан механизм параллельных кривошипов с дополнительным шатуном 5. Подсчет подвижности по формуле (5) дает

W = 3 ∙ 4 – 2 ∙ 6 = 0,

т.е. кинематическая цепь в общем случае представляет ферму с нулевой подвижностью. Однако если длины звеньев EF = BC = AD, а AE = DF и BE = FC, то наличие звена 5 не изменит движения шарнирного четырехзвенника ABCD, исключающего W = 1. Поэтому связь EF и называют избыточной.

В рассматриваемом механизме дополнительный шатун EF позволяет устранить лишнюю степень свободы в случае, когда при движении в этом механизме три центра вращения (постоянные или мгновенные) попадают на одну прямую (рис.2.9,б). В данном положении ведомое звено 3 может вращаться как в прямом, так и обратном направлениях.

Показательным в этом отношении является пример зубчатого механизма планетарного типа, изображённый на рис. 2.13.

Рис.2.13

В состав механизма входит центральное колесо 1, являющееся ведущим, три параллельно работающих сателлита 2 и стержневое звено 3, образующее вращательные пары с сателлитами. Все подвижные звенья размещены внутри неподвижного колеса 0 с внутренними зубьями. Данные для расчёта таковы: количество пар 5-го класса p₅=5 (они на схеме отмечены римскими цифрами), каждый сателлит 2 образует зацепление (две кинематические пары) с колёсами 0 и 1, поэтому p₄=6, количество подвижных звеньев механизма n=5, количество степеней свободы механизма W=1. В результате расчёта получаем

q= (2p₅ + p₄) – (3n – W) = (2∙5 + 6) – (3∙5 - 1) = 2.

Таким образом, видим, что в данном механизме имеется две избыточных связи, это – два из трёх сателлитов, которые повторяют функции одного сателлита. Следует отметить, что в обоих механизмах избыточные связи играют положительную роль, разделяя общий силовой поток и уменьшая нагрузку на звенья.

Избыточные связи могут играть и отрицательную роль, когда они ограничивают движение звена в кинематической паре, уже ограниченное связью в другой кинематической паре. Рассмотрим, например, четырёхшарнирный механизм (рис. 2.13.1), все звенья которого образуют друг с другом только вращательные кинематические пары 5-го класса.

Рис.2.13.1

При идеальном изготовлении звеньев оси всех шарниров должны быть параллельны друг другу (на рис. 2.13.1 отмечены только шарниры шатуна A и B), и механизм должен легко собираться и нормально функционировать. Так как точно изготовить звенья невозможно, то в результате ошибок оси шарниров перекашиваются, звенья уходят из одной плоскости, и механизм становится пространственным (на рис. 2.13.1 такой механизм изображён штриховыми линиями, и шарниры шатуна занимают положение и ). Для возвращения его в плоское состояние необходимо приложить немалые усилия. Однако после такой операции звенья деформируются, в кинематических парах образуется кромочный контакт, и всё это приводит к интенсивному износу элементов кинематических пар и к сокращению срока службы механизма. Чтобы обнаружить такого рода избыточные связи, необходимо рассматривать механизм как пространственный. Тогда формула и расчёт количества избыточных связей будет

q= 5p₅ – (6n – 1) = 5∙4 – (6∙3 - 1) = 3.

То есть в данном механизме имеются три избыточных связи. Для приведения механизма в работоспособное состояние необходимо вместо пар пятого класса по концам шатуна расположить пары третьего класса (сферические шарниры) и , которые в сумме дадут четыре дополнительных движения. При необходимых трёх движениях одно из них останется неиспользованным – а именно, вращательное движение вокруг собственной оси шатуна. Это движение будет местной подвижностью и на движение механизма в целом влиять не будет.

Количество местных подвижностей в механизме можно определить вычитанием количества потерянных степеней свободы (2p₅ + p₄) из того количества, которое должно быть потеряно для нормального функционирования механизма (3n – W). Если обозначить количество местных подвижностей буквой f, то получается следующая формула для расчёта этого количества

f= (3n – W) - (2p₅ + p₄).

Для кулачкового механизма (рис. 2.13.2) получается следующий результат.

Рис.2.13.2

Число подвижных звеньев n=3, число кинематических пар 5-го класса p₅=3, число кинематических пар 4-го класса p₄=1 и, наконец, W=1. Подставляя все эти данные в приведённую формулу, получаем

f= (3n – W) - (2p₅ + p₄) = (3∙3 - 1) – (2∙3 + 1) =1.

Этот расчёт показывает, что в механизме имеется одна лишняя степень свободы или местная подвижность. Местной подвижностью здесь является вращение ролика 2 относительно толкателя 3, так как это движение не участвует в преобразовании движения. В данном случае это движение необходимо для замены трения скольжения трением качения, что является более выгодным с точки зрения потерь на трение (повышение КПД).

На рис.2.14,а показан пятизвенный механизм двойного параллелограмма, выполненный по плоской схеме. В этом случае W_П=1 (одна обобщенная координата φ₁), n=4, p_Н=6, p_В=0. Следовательно, по формуле Чебышева q_n = 1 - 3∙4 + 2∙6 = 1, т.е. механизм статически неопределимый, с одной избыточной связью. Действительно, основной четырехзвенный механизм ABCD может быть собран без деформаций звеньев при любых (в некоторых пределах) длинах звеньев, однако, постановка дополнительного звена 5 произвольной длины невозможна, для сборки придется выполнить условие равенства длин параллельных звеньев, что практически возможно лишь при высокой точности изготовления.

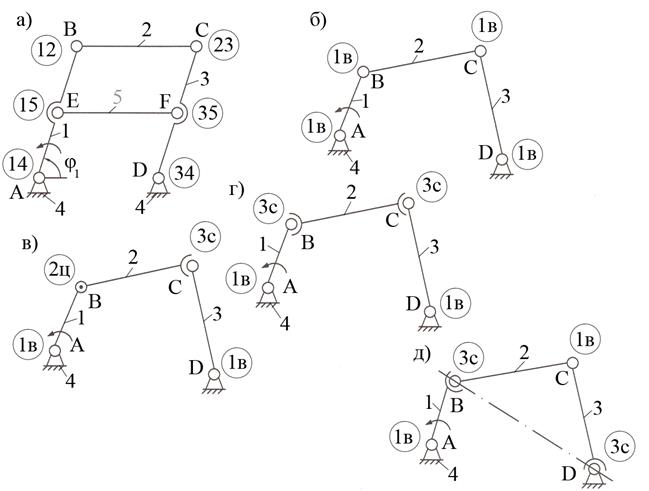
Рис.2.14

Следует отметить то обстоятельство, что при структурном анализе не учитывались зазоры в кинематических парах: благодаря им подвижность кинематической пары повышается и влияние избыточных связей несколько смягчается.

Полученный после удаления звена 5 плоский четырехзвенный механизм с четырьмя одноподвижными вращательными парами (W=1, n=3, p_Н=4, рис. 2.14,б) является оптимальным: q = 1 - 3∙3 + 2∙4 = 0. Реальный механизм за счет неточностей изготовления (например, вследствие непараллельности осей A и D) оказывается пространственным. По формуле Малышева тогда в механизме оказываются три избыточные связи:

q = W – 6n +5p₁ = 1 - 6∙3 + 5∙4 = 3.

Чтобы данный пространственный механизм был статически определимым, нужна его другая структурная схема, полученная понижением класса некоторых кинематических пар, например схема, изображенная на рис. 2.14,в, для которой q = W – 6n +5p₁ + 4p₂ + 3p₃ = 1 - 6∙3 + 5∙2 + 4∙1 + 3∙1 = 0. Это механизм оптимальной структуры, но стоимость его изготовления повышается.

Возможен вариант механизма (рис. 2.14,г) с двумя сферическими парами (p₁=2, p₃=2); в этом случае помимо основной подвижности механизма W₀=1 появляется местная подвижность W_M=1 – возможность вращения шатуна 2 вокруг своей оси BC. Эта подвижность не влияет на основной закон движения механизма и может быть даже полезна с точки зрения выравнивания износа шарниров B и C: при работе механизма шатун 2 может самопроизвольно поворачиваться вокруг своей оси за счет переменных динамических нагрузок и вибраций. Следовательно, W = W₀ + W_M=2 и формула Малышева подтверждает, что такой механизм будет оптимальным: q = 2 - 6∙3 + 5∙2 + 3∙2 = 0.

На рис.2.14,д показан вариант схемы механизма, который имеет групповую подвижность звеньев W_Г =1. Здесь две сферические пары установлены в шарнирах B и D, и звенья 2 и 3 будут иметь дополнительную общую (групповую) подвижность в виде возможного совместного вращения вокруг оси BD. Такой вариант механизма не допустим, т.к. поведение выходного звена становится не предсказуемым.

Механизмы с незамкнутой кинематической цепью собираются без натягов, поэтому они всегда оптимальны, без избыточных связей (q=0).

Итак, для реальных механизмов общее число степеней свободы определяется как W = W₀ + W_M + W_Г.

4. Локальные избыточные связи возникают в сложных кинематических парах. На рис. 2.15,а показан консольный вал 1, образующий со стойкой 2 вращательную пару V класса. Прогиб вала в точке С под действием силы F может иметь недопустимо большие значения.

Рис.2.15

Если вместо простой вращательной пары вал установить на двух опорах (рис. 2.15,б), то прогиб вала может быть уменьшен, но такая сложная кинематическая пара дает 5 избыточных связей: W=1, n=1, p₁=2; q = 1 - 6∙1 + 5∙4 = 5 Число избыточных локальных связей в кинематической паре, способствуя уменьшению податливости конструкции, может оказаться вредным в случае изменения температурного режима работы, при деформации стойки, при отклонениях размеров, формы и расположения поверхностей элементов кинематической пары. Поэтому число избыточных локальных связей приходится уменьшать. Так, если для вала правый подшипник выполнить четырехподвижным линейным II класса (рис. 2.15,в), то число связей будет уменьшено до двух, и прогиб вала в точке С (при а=в) уменьшится в 8 раз по сравнению с консольной установкой вала (рис. 2.15,а). Если оба подшипника выполнить со сферическими элементами (рис.2.15,г), причем левый подшипник неподвижен в осевом направлении (фиксированная опора), а правый имеет осевую подвижность (плавающая опора), то максимальный прогиб от нагрузки F в точке С (при а=в) уменьшится только в два раза по сравнению с консольной опорой вала только на левом конце (рис.2.15,а), однако вал будет статически определимым: q = 1 - 6∙1 + 2∙1 +3∙1=0.

При выполнении структурного анализа механизмов избыточные связи и местные подвижности должны быть исключены.

Рассмотрим примеры исследования кинематических цепей.

Пример 4.

Рассмотрим пример на определение числа степеней свободы замкнутой кинематической цепи (рис.2.16).

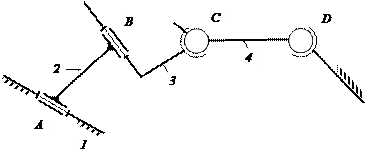
Рис. 2.16. Четырехзвенный пространственный механизм (к примеру 4)

Решение.

Звенья 1 (стойка) и 2 входят в пару A (V класса), звенья 2 и 3 – в пару B (V класса), звенья 3 и 4 – в пару С (IV класса) и, наконец, звенья 4 и 1 (стойка) входят в пару D (III класса). Число подвижных звеньев: n=3;

число пар V класса p₅ равно двум;

число пар IV класса p₄ равно единице;

число пар III класса p₃ также равно единице.

Подставляя числа звеньев и пар в формулу (4), получаем

W = 6n – 5p₅ – 4p₄ – 3p₃ =6∙3 – 5∙2 – 4∙1 – 3∙1 = 1,

т. е. рассматриваемая кинематическая цепь обладает одной степенью свободы.

Пример 5.

Определить число степеней свободы незамкнутой кинематической цепи, показанной на рисунке 2.17.

Рис. 2.17. Незамкнутая пространственная кинематическая цепь (к примеру 5)

Решение.

Звенья 1 (стойка) и 2 входят в пару A (III класса),

звенья 2 и 3 – в пару B (IV класса),

звенья 3 и 4 – в пару С (V класса).

Число подвижных звеньев: n=3.

Подставляя числа звеньев и пар в формулу (4), получаем

W = 6n – 5p₅ – 4p₄ – 3p₃ =6∙3 – 5∙1 – 4∙1 – 3∙1 = 6,

т. е. рассматриваемая кинематическая цепь обладает шестью степенями свободы.

Пример 6.

На рисунке 2.18 представлен механизм поперечно - строгального станка.

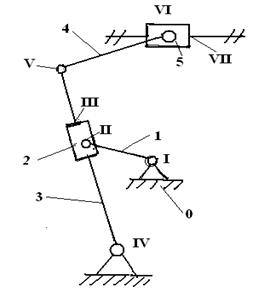
Рис.2.18. Механизм поперечно - строгального станка (к примеру 6)

Обозначим номера подвижных звеньев данной схемы арабскими цифрами, их количество составит n = 5, римскими цифрами обозначим номера кинематических пар 5-го класса, получив их количество p₅ = 7, пары 4-го класса в этом механизме отсутствуют, т. е. p₄ = 0. Расчёт по формуле Чебышева (5) даёт

W = 3n - 2p₅ – p₄ = 3∙5 - 2∙7 - 1∙0 = 1.

Следовательно, в этом механизме одна степень свободы, что означает необходимость выбрать одно ведущее звено для его нормального функционирования.

Структура механизмов

Среди всего многообразия конструкций механизмов различают: стержневые (рычажные), кулачковые, фрикционные, зубчатые механизмы, механизмы с гибкими звеньями (например, ременные передачи) и др. виды.

Менее распространенные классификации подразумевают наличие механизмов с низшими или высшими парами в плоском или пространственном исполнении и т.д.

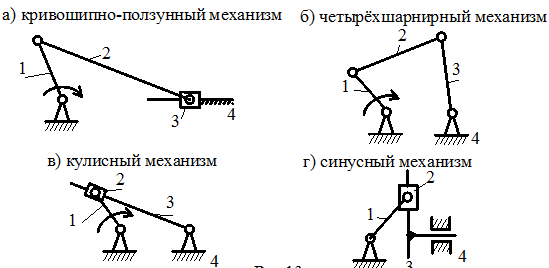
Рис.2.19

Учитывая возможность условного превращения практически любого механизма с высшими парами в рычажный, в дальнейшем наиболее подробно рассматривается именно эти механизмы, а структурные схемы других механизмов изложены в соответствующих разделах.

Рычажные механизмы применяют в машинах, приборах и аппаратах для обеспечения требуемого движения рабочего органа. В рычажных механизмах, в отличии от зубчатого, кулачкового и других механизмов, каждое из звеньев представляет собой рычаг. Достоинства рычажных механизмов перед другими типами механизмов состоят в способности передавать большие силы, разнообразии движения выходного звена, высокой надежности, сравнительно низкой стоимости и др.

Среди рычажных механизмов наиболее распространенны так называемые четырехзвенные, примеры которых представлены на рис.2.19,а-г.

Виды звеньев (рис. 2.20 и рис.2.21):

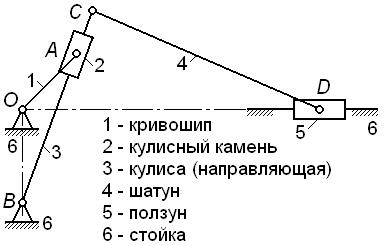
Рис.2.20

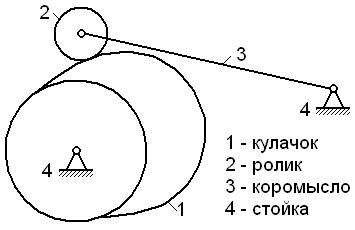
Рис.2.21

стойка – звено, принимаемое за неподвижное; такое звено в механизме может быть только одно;

кривошип – вращающееся звено рычажного механизма, которое может совершать полный оборот вокруг неподвижной оси;

коромысло – вращающееся звено рычажного механизма, которое может совершать только неполный оборот вокруг неподвижной оси;

шатун – звено рычажного механизма, образующее кинематические пары только с подвижными звеньями;

кулиса – звено рычажного механизма, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару; в зависимости от степени протяженности элемента поступательной пары различают «камень» (звено меньшей протяженности) и «направляющую»;

ползун – звено рычажного механизма, образующее поступательную пару со стойкой;

кулачок – звено, имеющее элемент высшей пары, выполненный в виде поверхности переменной кривизны;

камень – звено, совершающее поступательное движение относительно подвижной направляющей, называемой кулисой;

зубчатое колесо – звено с замкнутой системой зубьев, обеспечивающее непрерывное движение другого зубчатого колеса или рейки.

Количество типов и видов механизмов исчисляется тысячами, поэтому классификация их необходима для выбора того или иного механизма из большого ряда существующих, а также для проведения синтеза механизма.

Универсальной классификации нет, но наиболее распространены 3 вида классификации:

Функциональная. По принципу выполнения технологического процесса механизмы делятся на механизмы: приведения в движение режущего инструмента; питания, загрузки, съёма детали; транспортирования и т.д.;

Структурно-конструктивная. Предусматривает разделение механизмов как по конструктивным особенностям, так и по структурным принципам. К этому виду относят механизмы: кривошипно-ползунный; кулисный; рычажно-зубчатый; кулачково-рычажный и т.д.;

Структурная. Проста, рациональна, тесно связана с образованием механизма, его строением, методами кинематического и силового анализа, была предложена Л.В. Ассуром в 1916 году и основана на принципе построения механизма путем наслоения (присоединения) кинематических цепей (в виде структурных групп) к начальному механизму. Согласно этой классификации, любой механизм можно получить из более простого присоединением к последнему кинематических цепей с числом степеней свободы W = 0, получивших название структурных групп, или групп Ассура. Недостаток классификации – неудобство для выбора механизма с требуемыми свойствами.

Классификация плоских механизмов по Л. В. Ассуру

Основной принцип образования механизмов был впервые сформулирован в 1914 г. русским ученым Л.В.Ассуром.

Он состоит в следующем. Схема любого механизма может быть составлена последовательным присоединением к начальному звену (к начальным звеньям) группы звеньев с нулевой степенью подвижности относительно тех звеньев, к которым группа присоединяется (рис.2.21.1).

Рис.2.21.1

Начальное звено и стойку, образующие кинематическую пару V класса, называют механизмом I класса. Механизм должен иметь число начальных звеньев, равное числу его степеней свободы. В целом группа начальных звеньев со стойкой образует исходный механизм. Группы звеньев с нулевой подвижностью носят названия групп Ассура или структурной группой (в дальнейшем просто группой).

Группой Ассура будем называть кинематическую цепь с нулевой степенью свободы относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев, и не распадающуюся на более простые цепи, обладающие также нулевой степенью свободы. Таким образом, механизм можно представить в виде следующей блочной структуры:

Механизм

+

Группа начальных звеньев W = Wмех, механизм I класса

+

Группа Ассура Wгр = 0

+

Группа Ассура Wгр = 0

Из сказанного следует, что группа, присоединенная к стойке, имеет нулевую подвижность, но тогда она является и кинематически и статически определимой системой.

Для плоских механизмов, звенья которых образуют пары IV и V классов, группа Ассура отвечает условию

W_гр = 3n – 2р₅ – р₄ = 0. (6)

Входящие в состав плоского механизма высшие кинематические пары IV и V классов могут быть условно заменены кинематическими цепями, образованными только парами V класса.

При замене должны соблюдаться:

- структурная эквивалентность замены;

- кинематическая эквивалентность замены.

Если принять р₄ = 0, то соотношение звеньев и пар в группе

W = 3n - 2p₅ =0.

или

Из (7) заключаем, что группа может состоять только из четного числа звеньев, число пар пятого класса в группе всегда в полтора раза больше числа звеньев. Те пары, с помощью которых группа присоединяется к механизму, называют внешними, их количество определяет порядок группы; остальные пары, посредством которых звенья группы соединяются между собой, называют внутренними.

Все структурные группы принято разделять на классы – со 2-го по 4-й.

Класс структурной группы (по И.И. Артоболевскому) определяется числом кинематических пар, образующих наиболее сложный замкнутый контур группы.

Самая простая структурная группа (n=2, p₅=3) состоит из двух звеньев и трех пар. Это группа II класса 2-го порядка или двухповодковая группа. Поводки – это звенья группы, обладающие свободным элементом кинематической пары, служащим для присоединения группы к механизму.

Порядок структурной группы равен числу свободных кинематических пар, которыми группа присоединяется к более простому механизму. Свободные пары показаны стрелками (рис. 2.22).

Структурная группа 2-го кл., 2-го порядка (все структурные группы 2-го кл. имеют 2-й порядок)

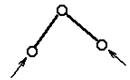
Структурная группа 3-го кл., 3-го порядка

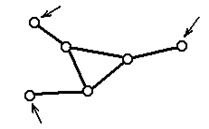
Структурная группа 4-го кл., 2-го порядка

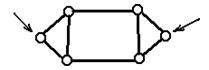
Рис. 2.22. Примеры структурных групп различных классов

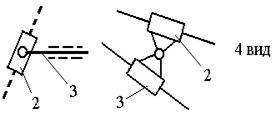
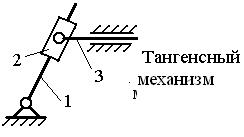
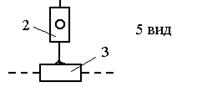
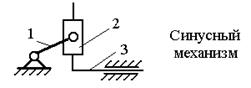
Наиболее распространённые структурные группы 2-го класса подразделяются на 5 видов (модификаций) (см.табл.3).

Таблица 3.

Кинематическая схема структурной группы, вид	Механизм, содержащий такую структурную группу

Примечание. 1 – ведущее звено; 2 и 3 – звенья, образующие структурную группу.

Т.к. кинематические пары V класса могут быть вращательными и поступательными, двухповодковые группы имеют пять видов, различающихся числом и местом размещения поступательных пар (рис. 2.23). Штриховой линией показана условная стойка, обеспечивающая нулевую степень подвижности группы.

Рис.2.23

На рис. 2.24,а показана группа III класса 3 порядка или трехповодковая группа со звеном 4, входящим в три кинематические пары; такое звено называют базисным. На рис. 2.24,б показана группа IV класса 2 порядка. Обе группы имеют одни вращательные пары, но они могут содержать одну или несколько поступательных пар и имеют соответственно большее число видов.

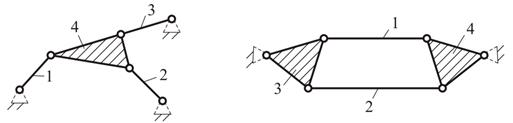
а) б)

Рис.2.24

Могут быть образованы группы и более высоких классов, но они редко применяются в реальных механизмах.

Примеры структурных групп и начального механизма приведены на рис. 2.25.

- Двухповодковая структурная группа 2-го кл.

- Структурная группа 2-го кл.

- Структурная группа 3-го кл.

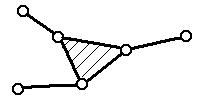
- Структурная группа 4-го кл.

- Механизм 1-го кл. (начальный механизм)

Рис. 2.25. Примеры структурных групп

Механизмам присваивается определённый класс, соответствующий наивысшему классу входящих в него структурных групп. Примеры механизмов различных классов приведены на рис. 2.26.

При добавлении к механизму 1-го класса различных структурных групп можно получить механизм, состоящий из одной или нескольких структурных групп и механизма 1-го класса.

Класс механизма определяет методику кинематического и силового анализа механизма. С повышением класса механизма методики расчета усложняются, поэтому всякий раз нужно стремиться подбирать в качестве начального звена такое, при котором класс механизма будет как можно ниже.

Не путать класс механизма и класс структурной группы.

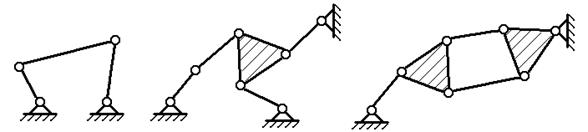
2-й кл. 3-й кл. 4-й кл.

Рис. 2.26. Механизмы различных классов

Для определения класса механизма его расчленяют на структурные группы, начиная с конца механизма. За начало механизма принимают ведущее звено (начальный механизм).

От конца механизма отделяются поочерёдно простейшие структурные группы до тех пор, пока не останется лишь механизм 1-го класса (начальный механизм, их может быть несколько).

По классу структурных групп определяют класс механизма. Количество начальных механизмов равно величине W.

Пример расчленения плоского рычажного механизма на структурные группы показан на рис. 2.27. Предварительно вычисляют степень подвижности механизма W по формуле Чебышева (5)

W_гр = 3n – 2р₅ – р₄ = 0.

В данном случае W =1, а это значит, что в механизме должны быть одно ведущее звено и соответственно один начальный механизм.

а б в г

Рис. 2.27. Расчленение механизма на структурные группы: а – исходный механизм; б – начальный механизм;

в – 2-й класс, 1-й вид; г – 2-й класс, 2-й вид

После отсоединения от механизма всех структурных групп останется стойка и начальные звенья в количестве W (речь идет о фактической степени подвижности механизма, рассчитанной после исключения пассивных связей и местных подвижностей). Каждое начальное звено со стойкой называют начальным механизмом; таким образом, механизм состоит из W начальных механизмов и некоторого количества структурных групп, присоединенных в строго определенном порядке, который отражают в специальной записи, называемой формулой строения. Например, механизм с двумя степенями свободы, содержащий шесть структурных групп, может иметь такое строение

В зависимости от количества звеньев в группе и способа их соединения между собой группы делят на классы.

Все двузвенные группы (n=2; p₅=3) являются группами II класса второго порядка; дополнительно эти группы, в зависимости от количества поступательных пар, использованных при их формировании, делятся на виды (рис. 2.28).

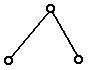
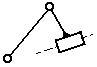
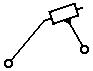
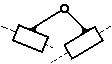
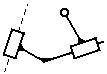
1 вид 2 вид 3 вид 4 вид 5 вид

Рис. 2.28. Группы II класса

Класс групп, состоящих более чем из двух звеньев, определяется числом вершин (или сторон) многоугольника, образуемого внутренними кинематическими парами на структурной схеме группы, которая строится по следующим правилам:

- все вращательные и поступательные пары пятого класса изображают на этой схеме как вращательные;

- звенья, участвующие в нескольких кинематических парах, изображаются в виде соответствующих многоугольников.

На рис. 2.29 и 2.30 для удобства сопоставления помещены рядом друг с другом кинематические и структурные схемы двух групп различных классов.

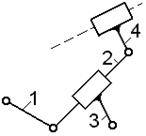
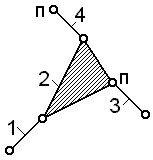
а) б)

Рис. 2.29. Группа III класса 3 порядка: а – кинематическая схема, б – структурная схема

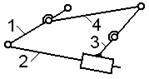
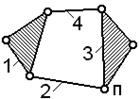
Рис. 2.30. Группа IV класса 2 порядка: а – кинематическая схема, б – структурная схема

На структурной схеме для большей наглядности можно те шарниры, которым на кинематической схеме соответствуют поступательные пары, помечать буквой «п».

В структурных схемах групп III класса внутренние шарниры образуют один или несколько треугольников жесткой (неизменяемой) конфигурации; в схемах групп более высоких классов встречаются многоугольники (изменяемой конфигурации) с четырьмя и большим числом сторон, которое и определяет класс группы.

Отметим, что классификации Л.В.Ассура подчиняются только те плоские механизмы, у которых начальные звенья образуют кинематические пары со стойкой.

Структурный синтез рычажных механизмов

Теория структуры, изложенная выше, позволяет решать некоторые задачи синтеза механизмов. Например, используя формулу Сомова–Малышева, можно определить, какое количество звеньев может иметь простейший пространственный механизм, в составе которого только пары пятого класса. Для такого механизма формула приобретает вид W = 6n - 5p₅.

Из неё следует, что количество кинематических пар 5-го класса в механизме должно быть При одном ведущем звене (W=1) целое число пар получится, если n = 6. Таким образом, получается семизвенный механизм, состоящий из шести подвижных звеньев и стойки. Аналогично, но более трудоёмко, решается задача синтеза пространственного механизма с разными сочетаниями кинематических пар различных классов.

С привлечением формулы Чебышева можно решать задачи в той же постановке и для плоского механизма. Выразив из этой формулы количество звеньев, получим

Пусть в механизме W=1 (одно ведущее звено), количество пар 4-го класса p₄=0. При этих данных минимальное количество пар 5-го класса для получения n целого должно быть p₅=4. Подставляя эти данные в приведённую формулу, получаем n = 3. Так приходим к четырёхзвенному механизму (три подвижных звена и стойка).

Если в механизм ввести одну кинематическую пару 4-го класса (высшую пару), то для целого n достаточно p₅=2, а в итоге расчёта получим n = 2. Такой механизм является трёхзвенным с высшей парой, примером которого служит простейший зубчатый механизм, включающий два зубчатых колеса и стойку (рис. 2.31, а), или кулачковый механизм (рис. 2.31, б).

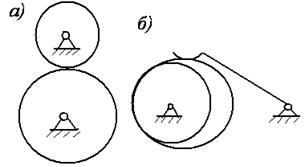
Рис.2.31

Согласно принципу образования механизмов по Л. В. Асуру, необходимо помнить, что кроме ведущего звена и стойки все звенья механизма должны быть в составе групп Ассура. Это необходимо учитывать при структурном синтезе механизма. Например, требуется создать механизм для преобразования вращательного движения ведущего звена в возвратно-поступательное движение ведомого звена (рис. 2.32, а). Сколько звеньев необходимо установить между ними? Самый простой вариант ответа – одно звено (рис. 2.32, б). Если полученный механизм по его свойствам не устраивает конструктора, то как действовать дальше, сколько звеньев нужно установить между первым и последним звеньями? Ответ – три звена, которые вместе с ведомым звеном составят или две группы Ассура второго класса (рис. 2.32, в), или одну группу третьего класса (рис. 2.32, г). Между первым вариантом с одним промежуточным звеном и двумя другими вариантами с тремя промежуточными звеньями решения нет.

Рис.2.32

На рис. 2.33 приведены примеры образования механизмов II класса (рис. 2.33,а) и III класса (рис. 2.33,б).

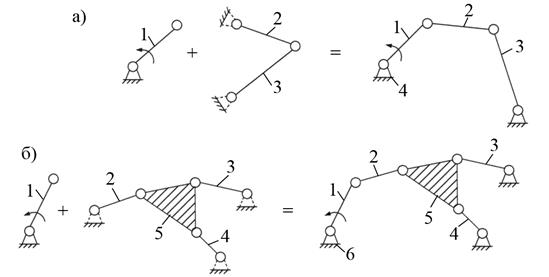
Рис.2.33

Второй метод синтеза состоит в преобразовании одного из звеньев структурной группы в два звена, образующих поступательную кинематическую пару V класса. На рис. 2.34,а,б представлены структурные группы и гидрорычажные механизмы соответственно II и IV классов, образованные этим методом.

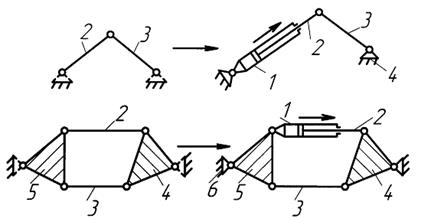
Рис.2.34

Следует отметить, что для механизмов с гидроприводом заданным является относительное движение поршня 2 в цилиндре 1, поэтому их структурный анализ по Ассуру не возможен. Механизм должен рассматриваться как неделимая структурная единица – гидрорычажный механизм соответствующего класса.

Условное преобразование механизма (замена высших кинематических пар низшими)

Для любого плоского механизма, содержащего высшие кинематические пары, можно построить так называемый заменяющий механизм, который не содержит высших пар, но эквивалентен заменяемому механизму по следующим показателям:

1) в структурном отношении (имеет ту же подвижность);

2) в отношении кинематики (при тех же законах движения входных звеньев остаются прежними законы движения выходных, сохраняются также траектории и законы движения всех точек);

3) в силовом отношении.

После такой замены структурную классификацию и методы кинематического анализа механизмов с низшими парами можно распространить на кинематические цепи с высшими парами.

При этом необходимо выполнить следующие условия:

1) Количество связей, наложенных на относительное движение звеньев высшей пары заменяющей кинематической цепью должно остаться неизменным.

2) Мгновенное относительное движение звеньев высшей пары должно сохраниться.

Чем в принципе можно заменить кинематическую пару, входящую в кинематическую цепь? Только другой парой или частью кинематической цепи. Поэтому каждую высшую пару, которая в плоской схеме накладывает одну связь и является плоской двухподвижной парой, следует заменить двумя низшими (плоскими одноподвижными) парами и одним звеном, которые в сумме также вносят в кинематическую цепь одну связь. (Две низшие пары дают четыре тангенциальные связи, а одно звено – три степени свободы). Вид и расположение одноподвижных пар зависят от элементов высшей пары и определяются из второго условия – тождественности соответствующих связей. Как обеспечить выполнение этого условия, не составляя уравнений связей? Воспользуемся свойством избыточной связи не влиять на кинематику механизма!

Рассмотрим трехзвенный механизм (рис.2.35,а), в котором элементами высшей пары D являются окружности. Мысленно соединим звенья 1 и 2 дополнительным звеном (стержнем), присоединив его шарнирами в точках С₁ и С₂ (центрах кривизны профилей, образующих высшую пару), и зададим вращение звену 1. Так как при движении звеньев механизма расстояние между точками С₁ и С₂ не изменяется, то дополнительное звено является кинематически пассивным, а вносимая им связь – избыточной. Теперь удалим из механизма высшую пару D и, учитывая, что АС₁=const и BC₂=const, получим из исходного заменяющий механизм в виде шарнирного четырехзвенника (рис.2.35,б).

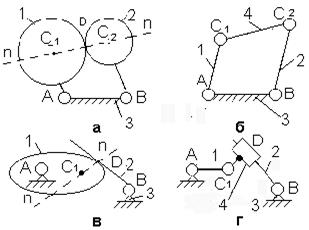
Рис.2.35. Схемы построений заменяющих механизмов:

а, в – исходные механизмы, б, г – заменяющие механизмы

Что собой будет представлять заменяющий механизм, если элементы высшей пары D (рис.2.35,а) выполнить в виде кривых переменной кривизны? При движении такого исходного механизма центры кривизны будут постоянно менять свое положение, а расстояние между точками С₁ и С₂, А и С₁, В и С₂ для каждого положения будут разными. Поэтому шарнирный четырехзвенник (рис.2.35,б) с определенными (фиксированными) значениями геометрических параметров будет заменяющим только для одного положения исходного механизма с высшей парой.

В общем случае при замене высшей пары заменяющий механизм является мгновенным рычажным механизмом, существующим только в одном положении.

Для замены плоской двухподвижной (высшей) пары через точку контакта соприкасающихся профилей проводят общую нормаль и на этой нормали находят центры кривизны профилей. Полагают, что в центрах кривизны имеются шарниры, которые соединяютс воображаемым звеном.

Если одно из звеньев исходного механизма имеет прямолинейный профиль (рис.2.35,в), то вместо шарнира вводят поступательную пару, которую можно считать шарниром с бесконечно удаленным центром (рис.2.35,г).

Конструктивное преобразование механизма

Конструктивным преобразованием механизма называют изменение соотношений размеров, формы, расположения звеньев, приводящее к качественно иным техническим решениям при сохранении структурной схемы или вида механизма. В основу конструктивного преобразования механизмов положено: совмещение функций звеньев; выполнение элементов шарниров и других кинематических пар большими по размерам, чем размеры звеньев; замена охватывающих элементов охватываемыми; размещение одних звеньев и элементов кинематических пар внутри других элементов кинематических пар; замена одних звеньев и кинематических пар другими звеньями и парами с теми же функциональными признаками

В кулисном механизме кулиса 3 может быть выполнена в виде охватывающего звена (рис.2.36,а) или в виде охватываемого звена (рис.2.36,б). В схеме (рис.2.36,в) функции кулисы и камня совмещены в звене 2, взаимодействующем с элементом шарнира С. Механизм радиально–поршневой гидромашины (рис.2.36,г) состоит из статора 1, ротора 3 и поршня 2. Функции кривошипа и шарнира А совмещены в элементе шарнира А, охватывающем все остальные звенья. Центр кривизны поверхности А смещен по отношению к центру шарнира С. Поршень 2 с поверхностью А образует высшую кинематическую пару В. Данный механизм кинематически эквивалентен кривошипно-кулисному механизму.

Рис. 2.36. Схемы механизмов, полученные в результате конструктивных преобразований

кулисного механизма: а, б – с низшими парами; в, г – с высшей парой

Если высшую пару в общем случае в плоских механизмах заменяют условно, то в любом плоском рычажном механизме промежуточное звено с двумя низшими парами всегда может быть исключено и заменено одной высшей парой.

Приведенные приемы могут быть использованы по отношению к другим механизмам. Они позволяют получать механизмы с различными габаритными размерами, силовыми и энергетическими характеристиками.

Порядок структурного исследования плоского механизма

1) Пронумеровать все звенья механизма (если номера звеньев не указаны); неподвижному звену (стойке) обычно присваивают последний номер.

2) Рассчитать степень подвижности механизма w и проанализировать полученный результат; при наличии местных подвижностей и (или) пассивных связей избавиться от них, и повторить расчет w – в результате должна получиться фактическая степень подвижности механизма.

3) Произвести замену всех высших кинематических пар фиктивными звеньями и низшими парами (замену следует производить непосредственно на кинематической схеме механизма, используя контактные нормали и центры кривизны профилей); подтвердить расчетом величину w – она должна остаться прежней.

Если кинематическая схема сложна для анализа, можно для облегчения изобразить структурную схему по описанным ранее правилам (при этом нумерация звеньев обязательно должны быть сохранена).

4) Выбрать начальные звенья механизма (если они не были заданы условием задачи): если после структурного исследования механизма будет выполняться его кинематический расчет, то начальные звенья совпадают с входными, т.е. с теми, которым заданы законы движения; при последующем силовом анализе механизма за начальные звенья принимают те, к которым приложены неизвестные внешние силы или вращающие моменты.

Написать формулу строения механизма по типу (4); каждому варианту выбора начальных звеньев соответствует единственный вариант этой формулы.

Вопросы для самопроверки

- В какой форме может быть представлена структурная модель механизма?

- Является ли структурной моделью механизма его структурная схема?

- Чем обобщенная структурная схема механизма отличается от структурной схемы и что у них общего?

- Чем отличаются структурные модели разных уровней?

- Какова цель структурного анализа?

- Что понимают под логическими приемами анализа и синтеза?

- Что называют звеном механизма?

- Что называют кинематической парой?

- Как классифицируются плоские кинематические пары?

- Что называется кинематической цепью?

- Как рассчитать подвижность плоского механизма?

- Какой физический смысл имеет подвижность механизма?

- Что собой представляет избыточная связь?

- Что такое местная подвижность (лишняя степень свободы)?

- В чём состоит принцип структурного образования механизмов по Л.В. Ассуру?

- Что такое исходный механизм?

- Что такое группа Ассура, как классифицируются группы Ассура?

- Что называют формулой строения механизма?

- По каким признакам классифицируют механизмы?

- Как осуществляется замена высших пар низшими?

- Перечислите признаки по которым классифицируются кинематические пары?

- Что называется моделью машины или механизма? Перечислите виды моделей механизмов?

- Что называют структурным анализом и структурным синтезом?

- Чем параметрический синтез механизма отличается от структурного?

- Что происходит со звеньями и кинематическими парами при жестком соединении механизмов?

- С чего начинается проектирование любого механизма?

- Как выбирается подходящая структурная модель при структурном синтезе?

- Каким образом при выборе структурной схемы механизма учитываются ее функциональные возможности?

- Что понимается под лишними степенями свободы?

- В каких случаях и почему в механизме могут появиться мгновенные подвижности?

- Что такое метод инверсии?

- Какую структурную модель следует использовать при синтезе многозвенного манипулятора промышленного робота с шестью степенями свободы?

- Что такое маневренность манипулятора?

- Какие связи в механизме называются избыточными?

- Какие избыточные связи полезны для работы механизма?

- Какими свойствами обладают статически определимые механизмы?

- Сформулируйте недостатки и достоинства конструкций механизмов с контурными избыточными связями.

- Какие подвижности в механизме называются местными или локальными?

- Чем кинематическая пара отличается от других подвижных соединений двух звеньев?

- Какими преимуществами и недостатками обладают низшие пары по сравнению с высшими?

- Что такое число степеней свободы механической системы?

- Что означает термин «начальная пара?

- Дайте определение понятия "подвижность механизма"?

- Напишите формулы для подсчета подвижности механизма для плоскости и для пространства?

- Как из кинематической цепи получить механизм?

- Чему равно минимальное число звеньев и кинематических пар в кинематической цепи?

- Чем кинематическая цепь отличается от механизма, состоящего из твёрдых тел?

- Напишите формулу для подсчета избыточных связей в механизме?

- Почему возникают ошибки при устранении избыточных связей?

- Как найти в механизме местные подвижности?

- Что такое ведомая цепь? Дайте определение.

- Какая структурная модель применяется для анализа структуры механизмов с незамкнутыми кинематическими цепями?

- Можно ли допускать присутствие местных подвижностей в пространственных структурных группах?

- Почему нельзя размещать сферическую пару между стойкой и входным звеном плоского механизма?

- Почему плоские самоустанавливающиеся механизмы называют квазиплоскими?

- Между какими величинами устанавливается связь с помощью структурных формул?

- Что можно подсчитать по формуле Гохмана?

- Докажите, что структурная группа в плоской схеме рычажного механизма с идеальными связями является статически определимой системой.

- Содержит ли величина W, входящая в структурные формулы, число лишних степеней свободы?

- Укажите элементы из которых состоит механизм в структурной классификации Ассура?

- Какие задачи решаются при структурном анализе механизма по Ассуру?

- Как определяется класс и порядок механизма по Ассуру и по Артоболевскому?

- Как определить класс и число степеней свободы плоского механизма?

- Существуют ли механизмы, состоящие только из ведущей или только ведомой цепей?

- Как определить класс, порядок и вид группы Ассура?

- Может ли один и тот же механизм быть и не быть механизмом II класса?

- Если сравнить механизм с поездом, то чем в последнем будет структурная группа?

- В чем принципиальное различие с точки зрения структуры между структурной моделью третьего уровня и остальными моделями?

- Дайте определения понятиям: механизм; звено; кинематическая пара; кинематическая цепь; кинематическое соединение.

- Определите понятие «обобщенная координата механизма».

- Что такое «степень подвижности механизма»? В каких случаях возникают местные подвижности и пассивные связи? Как влияет на степень подвижности механизма наличие в его схеме кратных шарниров?

- Опишите цели замены высших кинематических пар низшими и порядок такой замены.

- Что представляют собой структурная группа и начальный механизм?

- По каким признакам устанавливают класс и порядок структурной группы?

- Какие звенья выбирают в качестве начальных при кинематическом анализе механизма? То же – при силовом анализе?

- Опишите последовательность структурного анализа плоского механизма.

- По какому признаку кинематические пары разделяются на высшие и низшие?

- Является ли указанная на рисунке кинематическая цепь механизмом? Сколько звеньев и кинематических пар она содержит? Определите какая это цепь - замкнутая или незамкнутая?

- Могут ли высшие кинематические пары обеспечить: а) вращательное; б) сферическое относительные движения звеньев? Ответ обоснуйте.

- Какую кинематическую пару образуют звенья 1 и 2 на рисунке и почему?

- Сколько звеньев и кинематических пар (низших и высших) включает механизм, указанный на рисунке?

- Звенья 1 и 3 соединены тремя одинаковыми по длине параллельными упругими нерастяжимыми нитями 2 (см.рис.). Какой кинематической паре кинематически эквивалентно данное соединение? Как должны быть расположены нити, чтобы соединение было эквивалентно трехподвижной сферической паре?

- Изобразите схему подвижного соединения двух звеньев, обеспечивающего относительное прямолинейно-поступательное движение звеньев вдоль трех осей декартовой системы координат. Какая кинематическая пара эквивалентна данному соединению? Можно ли назвать это соединение двух звеньев кинематическим соединением?

- Существует ли двухподвижная плоскостная пара? Обоснуйте свой вывод. Если такая пара существует, то изобразите ее эскиз?

- Изобразите схему кинематического соединения, содержащего только вращательные кинематические пары, кинематически эквивалентного трехподвижной сферической паре?

- Какие кинематические пары позволяют передавать: а) силу F_х вдоль оси х декартовой системы координат и пары сил с моментами M_z, M_y; б) три момента M_x, M_y, M_z?

- В справочной литературе даны следующие определения: «Замкнутая кинематическая цепь – кинематическая цепь, каждое звено которой входит не менее чем в две кинематические пары. Незамкнутая кинематическая цепь - система связанных кинематическими парами звеньев, которые не образуют замкнутых контуров». Докажите, что приведенные определения противоречат друг другу.

- В учебниках даны следующие определения: «Пары с линейным и точечным соприкосновением элементов называют высшими. Если элементы в кинематической паре конгруэнтны, т.е. поверхности совпадают во всех своих точках, то пару называют низшей». Можно ли согласиться с данными определениями и почему?

- Изобразите эскизы конструкций вращательной и поступательной кинематических пар. Какую пару проще изготовить?

- В учебном пособии утверждается, что вращательные и поступательные кинематические пары могут быть как низшими (подшипники скольжения), так и высшими (шариковые и роликовые подшипники качения). Какие ошибки с точки зрения современной терминологии допущены в данном суждении?

- Найдите правильное определение кинематической пары среди перечисленных:

а) непосредственное подвижное соединение двух звеньев;

б) соединение двух звеньев, допускающее их относительное движение;

в) соединение соприкасающихся звеньев, допускающее их относительное движение;

г) соединение двух соприкасающихся звеньев, допускающее их относительное движение;

д) соединение двух соприкасающихся звеньев.

- Найдите правильное определение механизма среди перечисленных:

а) система твердых тел, подвижно связанных путем соприкосновения и движущихся определенным, требуемым образом относительно одного из них, принятого за неподвижное;

б) система тел, предназначенная для преобразования движения одного или нескольких тел в требуемые движения других тел;

в) система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел;

г) система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других тел.

- Найдите правильное определение высшей кинематической пары среди перечисленных:

а) кинематическая пара с линейным и точечным соприкосновением элементов;

б) кинематическая пара, которая может быть выполнена соприкосновением элементов ее звеньев только по линиям и в точках;

в) кинематическая пара, в которой требуемое относительное движение звеньев может быть получено только соприкосновением ее элементов по линиям и в точках;

г) кинематическая пара с контактом звеньев по линии и в точке.

- Докажите, что определение звена механизма, принятое в теории механизмов, является неточным. Дайте свое определение звену механизма.

- В учебном пособии приводится следующее утверждение: «Кинематическую пару можно рассматривать как двухзвенную незамкнутую кинематическую цепь, предназначенную для воспроизведения требуемого относительного движения звеньев». Можно ли согласиться с данным утверждением и почему?

- В теоретической механике в расчетных схемах для соединения двух тел 1 и 2 часто используют цилиндрическую шарнирно – подвижную опору (рис.а) и стержень с шарнирами А и В на концах (рис.б). Чем являются эти опоры: кинематическими парами, кинематическими соединениями или чем-то другим? Сколько условий связи на относительное движение звеньев 1 и 2 в плоскости чертежа накладывают эти опоры?

- Из каких структурных элементов состоит кинематическая пара?

- Чему равно минимальное число звеньев и кинематических пар в кинематическом соединении? Обоснуйте ответ.

- Изобразите схему четырехподвижной кинематической пары с контактом звеньев в точках (4т).

- При каких условиях кинематическая пара с постоянным контактом звеньев в трех точках будет: а) поступательной; б) плоскостной; в) сферической; г) высшей (4Л); д) высшей (5Т) и почему?

- В литературе по теории механизмов утверждают, что в плоских и сферических механизмах на движения всех звеньев наложены 3 общие связи, а в цилиндрических – 4. Что понимается под термином общие связи?

- В учебном пособии утверждается, что при отклонении реальных поверхностей и профилей элементов кинематических пар от идеальных в парах появляются избыточные локальные связи и пары становятся статически неопределимыми. Можно ли согласиться с таким утверждением и почему?

- Докажите истинность или ложность следующего умозаключения, сделанного по аналогии. Из курса «Сопротивление материалов» известно, что замкнутый плоский контур стержневой конструкции имеет три дополнительные внутренние связи – трижды статически неопределим. Каждый замкнутый контур кинематической цепи плоского механизма с вращательными и поступательными парами имеет три нормальные избыточные связи и также трижды статически неопределим. Отсюда следует, что речь идет об одних и тех же связях, по-разному названных в теории механизмов и в сопротивлении материалов, поэтому нормальные избыточные связи есть дополнительные внутренние связи.

- Где следует расположить опору С (см.рис.), чтобы трехзвенная ферма стала кинематически изменяемой системой? Что является причиной появления мгновенной подвижности в ферме?

- Чему равно число степеней свободы и число местных подвижностей в кулачковом механизме, изображенном на рисунке?

- Где следует расположить шарнир А, чтобы статически определимая стержневая система, изображенная на рисунке превратилась из фермы в статически неопределимый механизм, если CF = DE = AB, CF||DE?

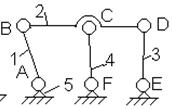
- Определите число избыточных связей в разветвленной кинематической паре А изображенной на рисунке? Что это за связи?

- Какие кинематические пары не содержат избыточных связей и являются статически определимыми?

- В учебном пособии утверждается, что низшие пары в плоских механизмах могут быть либо вращательными, либо поступательными. Почему нельзя согласиться с данным утверждением? Какие изменения необходимо внести в текст, чтобы утверждение стало истинным?

- Сколько сферических пар может быть в плоском четырехзвенном механизме с низшими кинематическими парами и замкнутой кинематической цепью?

- Объясните, почему при замене одной или двух вращательных пар на поступательные кинематическая цепь, изображенная на рисунке остается фермой, а при замене всех трех вращательных пар на поступательные превращается в механизм?

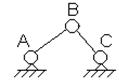
- Обоснуйте, может ли кинематическая цепь стойки из двух подвижных звеньев и трех поступательных пар иметь две степени свободы? Дайте примеры.

- Механизм шарнирного параллелограмма (см. рис.) имеет мгновенную подвижность, которая может привести к его заклиниванию. Для устранения этой подвижности в кинематическую цепь вводят кинематически пассивное звено. Изобразите структурную схему шарнирного параллелограмма в котором мгновенная подвижность отсутствует.

- Какую кинематическую пару образуют куб и вписанный в него шар? Дайте характеристики связям, наложенным на относительное движение звеньев.

- Какие плоские кинематические пары образуют звенья 1 и 2, изображенные на рисунке?

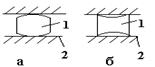
- Обоснуйте, отличаются ли требования к точности изготовления и монтажа кинематической пары при ее силовом или кинематическом замыкании?

- В чем основное сходство и различие понятий дополнительных связей, используемых в сопротивлении материалов, и избыточных связей, введенных в теории механизмов?

- В сопротивлении материалов, теоретической механике и теории механизмов используются структурные формулы, связывающие число стержней, контуров, шарниров с числом подвижностей стержневой системы. Почему с помощью структурных формул в общем случае нельзя установить, является ли стержневая система кинематически изменяемой или нет?

- В кривошипно-ползунном механизме двигателя внутреннего, изображенном на рисунке, сгорания ползун является входным звеном, а кривошип – выходным. Почему при кинематическом анализе механизма в качестве начального звена выбирается кривошип (рис.2.15), угол поворота φ₁ которого принимается за обобщенную координату, а не ползун?

- В учебном пособии приведена плоская «траекторная пара» – соединение звеньев 1 и 2, в котором звено 1 своими концами А и В скользит в прорезях f – f и s – s звена 2 (см.рис.). Элементами пары, принадлежащими звену 1, являются точки А и В, а элементами, принадлежащими звену 2, – плоские кривые f – f и s – s. Выполните классификацию «траекторной пары».

- Сформулируйте условия существования плоского механизма.

- С какой целью выполняют конструктивное преобразование механизмов?

- Можно ли использовать механизм для определения реакций в кинематических парах исходного механизма?

- Происходят ли при конструктивном преобразовании механизмов структурные изменения?

- В каких случаях необходимо выполнять условную замену высшей кинематической пары и строить заменяющий механизм?

- Зачем при расчленении механизма на структурные группы предварительно следует отсоединить из кинематической цепи кинематически пассивное звено?

- Почему переход от рычажного механизма (рис.2.35,г) к кулачковому (рис.2.35,в) механизму можно назвать конструктивным преобразованием механизмов, а обратный – нельзя.

- Найдите в механизме (см. рис.) кинематическое соединение, заменяющее высшую пару.

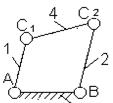
- Является ли приведенный на рисунке механизм кулачковым, а звено 1 кулачком? Обоснуйте свой ответ.

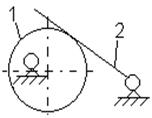
- Какой термин следует использовать для обозначения колеса с одним зубом.

- Классифицируйте по функциональному назначению, числу степеней свободы и структуре кинематической цепи кривошипно-ползунный механизм двигателя внутреннего сгорания.

- В учебном пособии механизмы эллипсографа (рис.3.11, б), синусный (рис.3.11, в) и тангенсный (рис.3.11, г) названы кулисными. Какие из перечисленных механизмов в соответствии с современной терминологией кулисными не являются и почему?

- Дайте названия всем звеньям механизмов, изображенным на рисунке.

- Может ли одно звено одновременно быть:

а) кулисой и направляющей;

б) камнем и шатуном;

в) ползуном и камнем;

г) кулисой и коромыслом;

д) камнем и кулисой;

е) шатуном и направляющей?

- Какое внутреннее противоречие присуще разделению механизмов на плоские и пространственные? Как избавиться от этого противоречия?

- Постройте заменяющий рычажный механизм для зубчатой передачи.

- Для механизма, изображенного на рисунке построить заменяющий механизм. Какое замыкание имеют кинематические пары С и D? Дайте характеристику механизму по виду звеньев и кинематических пар. Как называются звенья, образующие механизм?

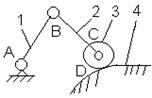
- Механизм пресса задан полуконструктивной схемой (см. рис.). Изобразите структурную схему механизма. Дайте название механизму и всем его звеньям.

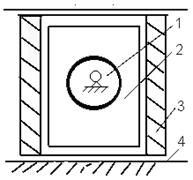
- В каких случаях при силовом расчете плоского механизма можно использовать условия равновесия плоской системы сил, а при прочностном расчете звеньев плоский механизм можно считать плоской фермой.

- Червяк, винт, зубчатое колесо. Что объединяет эти термины?

- Колесо радиусом r=0,5 м катится без скольжения по рельсу (см. рис.). Скорость точки В V_В=2м/с. Выполнить замену высшей кинематической пары и построить заменяющую кинематическую цепь. Найти с ее помощью скорости и ускорения точек А, В, С, D.

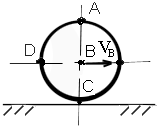
- Какое относительное движение звеньев допускает плоская высшая пара?

- Сформулируйте условия существования плоского рычажного механизма с незамкнутой кинематической цепью?

- Докажите, что определение кинематической пары, принятое в теории механизмов, является, с одной стороны, перегруженным, а с другой – неполным. Дайте свой вариант определения кинематической пары.

- Докажите возможность существования шестиподвижного соединения двух звеньев, обеспечивающего произвольное относительное перемещение этих звеньев. Как назвать такое соединение: кинематической парой, кинематическим соединением, чем – то другим?

- Предложите формулу для подсчета числа контуров произвольной кинематической цепи.

- Какой кинематической паре эквивалентен плечевой сустав человека?

- Какой кинематической паре эквивалентно соединение звеньев (см. рис.) 1 и 2 с жидким промежуточным элементом? Какие связи накладывает жидкость на относительные движения этих звеньев?

- Докажите, что не существует шарнирного четырехзвенника, для которого W = 1, q = 0.

- Почему в число структурных групп II класса (см.рис.) не вошла диада с тремя поступательными парами.

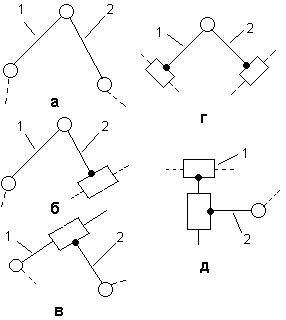
- Изобразите структурные схемы механизмов в соответствии со следующими формулами строения:

а) М=I₁(1,6)+II₃(2,3)+II₂(4,5);

б) М=I₁(3,6)+II₂(1,2)+II₂(4,5).

- Для пространственной структурной схемы четырехзвенника (см.рис.):

а) в результате визуального осмотра схемы найдите местные подвижности и оцените их влияние на работу механизма;

б) рассчитайте число избыточных связей q и q_τ.

4.8. Для кулачково-рычажного механизма (см.рис.):

а) рассчитайте число степеней свободы W, предварительно убедившись в результате визуального осмотра, что в механизме нет звеньев, вносящих избыточные связи; объясните полученный результат;

б) постройте заменяющий механизм и, расчленив его на структурные группы, определите класс, число степеней свободы и формулу строения механизма, приняв за начальное звено 6.

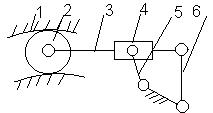
- Определите класс зубчато-рычажного механизма (см.рис.) и составьте формулу его строения, приняв за начальное звено 1.

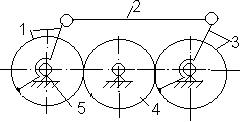
- Студент изобразил плоскую структурную схему в соответствии с формулой строения M = I₁(0,1)+II₄(2,3) и в недоумении заявил, что построенная им кинематическая цепь имеет W = 1, но механизмом не является. Докажите, что данная ситуация возможна, установите причины и изобразите эту кинематическую цепь.

- Три студента А, Б и В выполнили структурный анализ плоского механизма, используя для этого разные структурные модели. Студент А утверждает, что это элементарный некулачковый трехзвенный механизм и W = 1. Студент Б считает, что это механизм II класса и q_τ =0. Студент В утверждает, что в механизме три низшие пары и нет поступательных пар. Определите какой механизм изучали студенты, если один из них допустил ошибку.

- К какому уровню относится структурная модель, в которой механизм представляется состоящим из системы звеньев и системы связей между ними?

- Объясните, возможно ли, чтобы при анализе плоского механизма структурная группа, состоящая из двух звеньев (поводков) и трех вращательных кинематических пар, была с одной стороны, статически определимой, а с другой – статически неопределимой?

- Для механизма опрокидывания кузова автосамосвала (см. рис.) найдите W, q_τ, класс и формулу строения, если в качестве начального выбрано: а) звено 1; б) звено 4; в) звено 5;

- Механизм толкающего конвейера состоит из двух шарнирных четырехзвенников и двухзвенной структурной группы (см.рис.). Найдите указанные элементарные механизмы и укажите способ их соединения. Определите класс механизма, если начальное звено указано на схеме стрелкой.

- Для механизма, служащего для преобразования равномерного вращательного движения кривошипа в равномерное движение ползуна (см.рис.) найдите W, q_τ, класс и формулу строения, если в качестве начального выбрано: а) звено 1; б) звено 7;

- Выполните структурный анализ следующих механизмов:

а) ножниц для резки металла (см.рис.а); б) шлакового стопора – устройства для обслуживания шлаковых леток доменной печи (см.рис.б); в) двигателя внутреннего сгорания (см.рис.в).

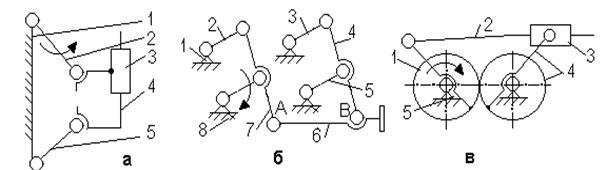
- Определите число степеней свободы W и количество подвижностей μ, характеризующих маневренность манипуляторов (см.рис.).

- Для механизма инверсора, у которого положение выходного звена изменяется обратно пропорционально положению входного звена (см.рис.) найдите W и класс.

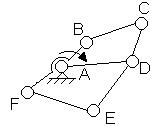
- Чему равны W, q_τ, q в механизме параллельных кривошипов (см.рис.), для которого АВ = CD = EF ?

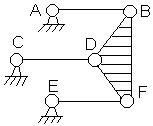
- Как изменятся структурные признаки (W, q_τ, q), если в механизме параллельных кривошипов вдвое увеличить длину EF = 2AВ ?

- Для зубчатого дифференциала с двумя сателитами 2, 5 (см. рис.): а) найдите k, W, q_τ, q; б) дайте характеристику всем избыточным связям и оценить их влияние на свойства механизма; в) расчлените механизм на ведущую и ведомую кинематические цепи с выделением структурных групп.

- Обоснуйте, можно ли при определении числа избыточных связей q плоского механизма с высшей парой использовать структурную схему заменяющего рычажного механизма?

- Обоснуйте, можно ли при построении структурной схемы механизма изображать:

а) двукратный шарнир как два однократных (см.рис.);

б) прямолинейную направляющую как криволинейную;

произвольно изменять:

в) длину звена (стержня);

г) положение шарнира на звене;

д) форму звена, образующего высшую пару, например круглый диск изображать как эллиптический;

е) направление оси вращательной пары?

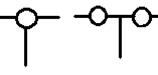
- Найдите правильное продолжение фразы. Для структурного анализа плоского механизма достаточно использовать…

а) обобщенную структурную схему;

б) схему, в которой указываются звенья и характер их взаимосвязи (вид кинематических пар);

в) упрощенную кинематическую схему, в которой указываются не размеры звеньев, а их соотношения, позволяющие найти связь между скоростями точек, но не сами скорости;

г) кинематическую схему – структурную схему с указанием размеров звеньев, необходимых для структурного анализа.

- Для плоского механизма (см.рис.) найдите k, W, q_τ, , класс.

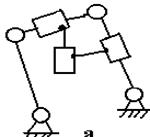
- Определите W, q_τ , класс для плоского механизма шагового конвейера (см.рис.).

- Выполните структурный анализ ременной передачи. Какую связь накладывает ремень на относительное движение шкивов?

- Найдите минимальное число звеньев и постройте структурную схему манипулятора, обеспечивающего перемещение объекта в пространстве вдоль осей x, y, z и его ориентацию (повороты вокруг осей x, y, z), с использованием только одноподвижных пар, три из которых–поступательные.

- Определите минимальное число звеньев и кинематических пар и изобразите структурную схему шарнирного механизма с замкнутой кинематической цепью при следующих условиях: W = 1, q = 0, все пары–вращательные. Сравните полученный механизм с шарнирными четырехзвенниками и объясните возможность существования последних.

- Спроектируйте самоустанавливающийся плоский зубчато–рычажный механизм (см. рис.).

- Используя метод наслоения структурных групп, найдите структурную схему плоского и пространственного кулисного механизма.

- Спроектируйте самоустанавливающийся плоский трехзвенный кулачковый механизм с тарельчатым (плоским) толкателем, преобразующий вращательное движение кулачка в возвратно-поступательное движение толкателя.

- Выведите структурную формулу для плоских клиновых механизмов, звенья которых не могут совершать вращательные движения, так как входят только в поступательные пары. Используя эту формулу, постройте структурную схему клинового механизма с минимальным числом звеньев, у которого W = 2.

- Сформулируйте признаки структурной группы в клиновом механизме. Что общего и в чем принципиальное различие структурных групп в трехзвенных зубчатом и клиновом механизмах? Используя принцип расчленения механизма на структурные группы, проверьте решение предыдущей задачи.

- Какая связь и почему будет между подвижностями составного и элементарных механизмов, если последние соединить:

а) с помощью неподвижных соединений к промежуточному звену?

б) одноподвижной или двухподвижной плоской кинематической парой?

в) структурной группой из двух звеньев?

- Предложите структурную схему плоского рычажного механизма переменной структуры на базе кривошипно-ползунного механизма.

- Предложите схему плоского самоустанавливающегося механизма шарнирного четырехзвенника с разгрузочными звеньями.

- Что представляет собой стержневая система (см. рис.), если оси аа и вв вращательных пар параллельны, а ось сс цилиндрической пары D не параллельна осям аа и вв?

1. Кинематически неизменяемая система.

2. Пространственный механизм.

3. Плоский несамоустанавливающийся механизм.

4. Плоский самоустанавливающийся механизм.

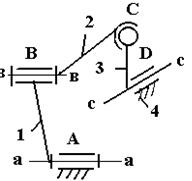
- Чем станет стержневая система (см. рис.), если ось сс цилиндрической пары D выполнить параллельной осям аа и вв?

- Чем станет стержневая система (см. рис.), если цилиндрическую пару D заменить вращательной, у которой ось сс не параллельна осям аа и вв?

- Чем станет стержневая система (см. рис.), если цилиндрическую пару D заменить вращательной, у которой ось сс параллельна осям аа и вв?

- Что такое звено механизма?

Ответ: твердое тело, состоящее из одной или нескольких деталей.

- Что такое анализ механизма?

Ответ: исследование структурных, кинематических или динамических свойств механизма.

- Из чего состоит механизм?

Ответ: из отдельных звеньев.

- Как называется каждая подвижная деталь или группа деталей, образующих одну жесткую систему тел в механизме?

Ответ: неподвижное звено (стойка).

- Сколько неподвижных звеньев в механизме?

Ответ: 1.

- Чем отличается механизм от кинематической цепи?

Ответ: наличием стойки.

- Как называется соединение двух соприкасающихся звеньев, допускающее их относительное движение?

Ответ: кинематическая пара.

- Как называется система звеньев, связанная между собой кинематическими парами?

Ответ: кинематическая цепь.

- Чему равен максимальный класс кинематической пары?

Ответ: 5.

- Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 5?

Ответ: S=6-H=6-5=1.

- Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 4?

Ответ: S=2.

- Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 3?

Ответ: S=3.

- Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 1?

Ответ: S=5.

- Назовите максимальное число условий связи?

Ответ: S=5.

- Назовите максимальное число степеней свободы звена кинематической пары в относительном движении?

Ответ: H=5.

- Чему равно число степеней свободы, если число условий связи равно 1?

Ответ: H=5, так как H=6-S.

- Чему равно число степеней свободы, если число условий связи равно 2?

Ответ: H=4.

- Чему равно число степеней свободы, если число условий связи равно 4?

Ответ: H=2.

- Чему равно число степеней свободы, если число условий связи равно 5?

Ответ: H=1.

- Как называется кинематическая пара, если ее звенья соприкасаются по поверхности?

Ответ: низшая кинематическая пара.

- Как называется кинематическая пара, если ее звенья соприкасаются по линии или в точке?

Ответ: высшая кинематическая пара.

- Напишите формулу Чебышева П.Л.

Ответ: W=3n-2p₅-p₄

- Как называется кинематическая цепь, степень свободы которой равна нулю?

Ответ: ферма.

- Как влияют лишние степени свободы на закон движения ведомого звена и однозначность его перемещения?

Ответ: никак.

- Напишите название кинематической пары, которая представляет собой шар, перекатывающийся со скольжением по плоскости?

Ответ: шар-плоскость.

- Напишите класс кинематической пары, которая представляет собой шар, перекатывающийся со скольжением по плоскости?

Ответ: 1 класс.

- Как называется кинематическая пара, представляющая собой цилиндр, лежащий на плоскости?

Ответ: высшая кинематическая пара 2-го класса.

- Напишите формулу Сомова-Малышева.

Ответ: W=6n-5p₅-4p₄-3p₃-2p₂-p₁.

- Начертите условное изображение пары шар-плоскость.

- Начертите условное изображение пары сферическая (шаровая).

- Начертите условное изображение пары: плоскостная.

- Начертите условное изображение пары: цилиндрическая.

- Начертите условное изображение пары: сферическая с пальцем.

- Начертите условное изображение пары: поступательная.

- Начертите условное изображение пары: вращательная.

- Начертите условное изображение пары: винтовая.

- Как классифицируют кинематические пары?

Ответ: по числу S (условий связи).

- Название пары, допускающей относительное вращательное движение звеньев вокруг оси.

Ответ: вращательная пара.

- Название пары, допускающей лишь прямолинейное поступательное относительное движение звеньев.

Ответ: поступательная пара.

- Название пары, допускающей независимое вращательное и поступательное относительные движения звеньев.

Ответ: цилиндрическая пара.

- Название пары, допускающей три независимых относительных вращения звеньев, вокруг осей x, y, z.

Ответ: сферическая пара.

- Как называется механизм, все подвижные звенья которого движутся в параллельных плоскостях?

Ответ: плоский механизм.

- Как называется механизм, подвижные звенья которого описывают траектории, лежащие в пересекающихся плоскостях?

Ответ: пространственный механизм.

- Что произойдет, если S=6?

Ответ: кинематическая пара становится жестким соединением деталей, т.е. одним звеном.

- Что произойдет, если S=0?

Ответ: пары не существует, а имеются два тела, движущихся независимо друг от друга.

- Что представляет собой механизм 1-го класса?

Ответ: это механизм, состоящий из подвижного звена и стойки.

- Чему равно число механизмов 1-го класса в механизме?

Ответ: число механизмов 1-го класса равно числу степеней свободы механизма.

- Как называется звено, совершающее полный оборот вокруг неподвижной оси?

Ответ: кривошип.

- Как называется подвижное звено (вращающееся, качающееся или движущееся возвратно-поступательно), которое является направляющей ползуна.

Ответ: кулиса.

- Что такое группа Асура?

Ответ: это кинематическая цепь с нулевой степенью подвижности, которая не распадается на более простые кинематические цепи, также обладающие нулевой степенью подвижности.

- Какое число звеньев должно быть в группе Асура?

Ответ: четное (2 или 4).

- На что подразделяются группы Асура?

Ответ: на классы, порядки и виды.

- Чем определяется порядок групп Асура?

Ответ: числом элементов, которыми она присоединяется.

- В каком году Ассур сформулировал принцип образования плоских механизмов?

Ответ: в 1914 г.

- Для каких механизмов подходит формула Чебышева для подсчета степени подвижности?

Ответ: для плоских.

- Что можно определить при помощи следующей формулы W=3n-2p₅-p₄?

Ответ: степень подвижности плоского механизма.

- В каких механизмах все звенья перемещаются в одной или параллельных плоскостях?

Ответ: в плоских.

- В каких механизмах звенья перемещаются в пересекающихся плоскостях?

Ответ: в пространственных.

- Что в формуле Чебышева обозначается как p₄?

Ответ: число кинематических пар 4-го класса.

- Что в формуле Чебышева обозначается как p₅?

Ответ: число кинематических пар 5-го класса.

- Что определяет формула Сомова-Малышева?

Ответ: степень подвижности пространственного механизма.

- Как определить число кинематических пар в сложном шарнире?

Ответ: подсчитать число соединяемых звеньев (подвижных и неподвижных) и вычесть единицу.

- Что такое машина?

Ответ: устройство для преобразования энергии, информации и материала.

- Что такое механизм?

Ответ: система звеньев, которая предназначена для преобразования одного движения в другое.

- Какое звено называется шатун?

Ответ: звено, совершающее сложное плоскопараллельное движение.

- Какое звено называется ползун?

Ответ: звено, совершающее поступательное прямолинейное движение.

- Какое звено называется коромысло?

Ответ: звено, которое совершает неполный оборот вокруг оси, связанной со стойкой.

- Чем отличается звено механизма от детали механизма?

Ответ: звено механизма состоит из одной или нескольких деталей.

- Что такое кинематическая цепь?

Ответ: система звеньев, связанных между собой кинематическими парами.

- Что такое кинематическая пара?

Ответ: подвижное соединение двух соприкасающихся звеньев.

- Сколько классов кинематических пар вы знаете?

Ответ: 5 классов.

- Напишите алгоритм определения класса кинематической пары.

Ответ: подсчитать число простейших движений, которыми обладает звено кинематической пары в относительном движении;

вычесть полученное число из шести, получив при этом число связей, налагаемых данной кинематической парой на относительное движение ее звеньев, и этим определим класс пары.

- Определить класс кинематической пары, образованной звеньями: шар-плоскость.

Ответ: S=6-H=6-5=1, 1 класс.

- Определить класс кинематической пары, образованной звеньями: плоскость-цилиндр.

Ответ: S=6-H=6-4=2, 2 класс.

- Алгоритм замены высшей кинематической пары на низшую.

Ответ: проводим нормаль через точку касания кривых и отмечаем на ней центры кривизны кривых, образующих вращательные пары, в которых соединяются условные звенья.

- С какой целью удаляют из механизма пассивные связи?

Ответ: чтобы упростить механизм, так как пассивные связи не оказывают никакого влияния на характер движения механизма.

- С какой целью удаляют из механизма лишние степени свободы?

Ответ: чтобы упростить механизм.

- С какой целью конструктора применяют в механизмах пассивные связи?

Ответ: для повышения его жесткости или для устранения неопределенности движения звеньев в некоторых положениях.

- С какой целью конструктора применяют в механизмах лишние степени свободы?

Ответ: для уменьшения сил трения и износа звеньев.

- Принцип образования плоских механизмов.

Ответ: последовательное присоединение кинематических цепей, являющихся группами Асура.

- Что такое механизм первого класса?

Ответ: это механизм с одной степенью свободы, состоящий из стойки и подвижного звена.

- Цель структурного анализа механизма.

Ответ: определить класс механизма.

- Алгоритм определения степени подвижности плоского механизма по формуле Чебышева.

Ответ: определить число подвижных звеньев, определить число кинематических пар, определить среди них высшие и низшие, посчитать по формуле Чебышева степень подвижности.

- Как определяется класс механизма.

Ответ: по максимальному классу группы Ассура, входящей в механизм.

- Что это значит, если по формуле Чебышева вы определили степень подвижности и она равна 0?

Ответ: это значит, что ни одно звено не может двигаться относительно неподвижного звена, и кинематическая цепь превращается в ферму.

- Что это значит, если по формуле Чебышева вы определили степень подвижности и она равна +2?

Ответ: это значит, что у механизма два ведущих звена.

- Из скольких звеньев состоит группа Асура 2-го класса?

Ответ: 2

- Из скольких звеньев состоит группа Асура 3-го класса?

Ответ: 3

- Из скольких звеньев состоит группа Асура 4-го класса?

Ответ: 4

- Как определяется порядок группы Асура?

Ответ: порядок равен числу поводков, которыми группа Асура присоединяется.

- Нарисуйте группу Асура 4-го класса.

Ответ:

- Нарисуйте группу Асура 3-го класса.

Ответ:

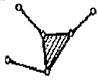
- Нарисуйте группу Асура 2-го класса 1-го вида.

Ответ:

- Нарисуйте группу Асура 2-го класса 2-го вида.

Ответ:

- Нарисуйте группу Асура 2-го класса 3-го вида.

Ответ:

- Нарисуйте группу Асура 2-го класса 4-го вида.

Ответ:

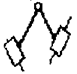
- Нарисуйте группу Асура 2-го класса 5-го вида.

Ответ:

Задачи для самостоятельного решения

Задача 1

Установить класс кинематической пары, образуемой плоской (1) и конической (2) поверхностями (конус касается плоскости только вершиной). По отношению к координатным осям xyz перечислить все виды допускаемых движений конуса относительно плоскости.

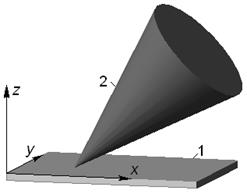
Задача 2

Для плоской кинематической пары, представленной на рисунке, установить:

- высшая пара, или низшая;

- класс кинематической пары;

- число подвижностей в относительном движении звеньев 1 и 2.

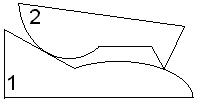
Задача 3

Конус 2 касается плоскости 1 своей образующей. Для кинематической пары, образуемой указанными звеньями, установить класс и число подвижностей в относительном движении звеньев 1 и 2 (назвать эти подвижности по отношению к какой-либо системе координат, связанной с плоскостью).

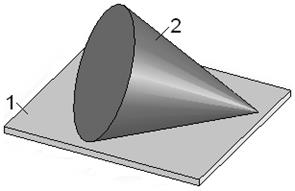
Задача 4

Конус 2 касается плоскости 1 кромкой своего основания, вершина конуса s удалена от плоскости на расстояние где – проекция вершины конуса на плоскость. Для кинематической пары, образуемой указанными звеньями, установить класс и число подвижностей в относительном движении звеньев 1 и 2 (назвать эти подвижности по отношению к какой-либо системе координат, связанной с плоскостью).

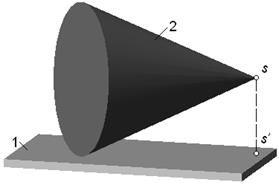
Задача 5

Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 9.

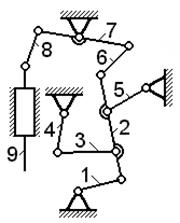
Задача 6 (см. рисунок к задаче 5)

Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 4.

Задача 7 (см. рисунок к задаче 5)

Для механизма с одной степенью свободы написать формулу строения механизма при начальном звене 5.

Задача 8

Для механизма с одной степенью свободы пронумеровать звенья и написать формулу строения механизма при начальном звене OA.

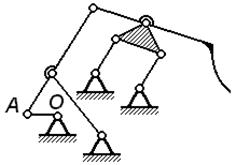
Задача 9

Считая звено 1 начальным, указать структурную группу, которую можно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).

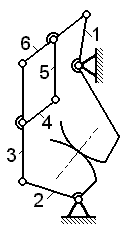
Задача 10 (см. рисунок к задаче 9)

Считая звено 2 начальным, указать структурную группу, которую можно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).

Задача 11

Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 9.

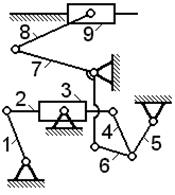
Задача 12 (см. рисунок к задаче 11)

Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 5.

Задача 13 (см. рисунок к задаче 11)

Считая звено 9 начальным, указать структурную группу, которую можно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).

Задача 14

Считая звено 1 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).

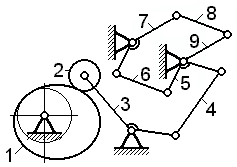
Задача 15

Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 4.

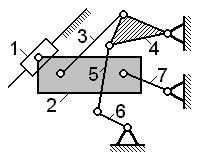
Задача 16 (см. рисунок к задаче 15)

Для механизма с одной степенью свободы указать номера звеньев, образующих группу III класса 3-го порядка при начальном звене 6.

Задача 17 (см. рисунок к задаче 15)

Считая звено 1 начальным, указать структурную группу, которую можно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).

Задача 18

Считая звено 1 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).

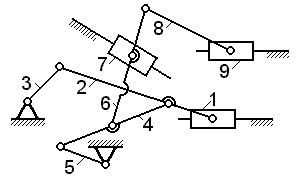
Задача 19 (см. рисунок к задаче 18)

Считая звено 5 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).

Задача 20 (см. рисунок к задаче 18)

Считая звено 3 начальным, указать две первые структурные группы, которые можно поочередно отсоединить от механизма, не нарушая его подвижности (ответ обосновать).

Задача 21 (см. рисунок к задаче 18)

Считая звено 5 начальным, указать номера звеньев, образующих группу III класса 3-го порядка.

Задачи 22 – 24

Для механизма с высшей кинематической парой построить заменяющий механизм; замену высшей пары произвести непосредственно на кинематической схеме. Написать формулу строения заменяющего механизма при начальном звене 4.

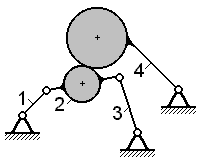
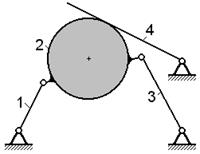
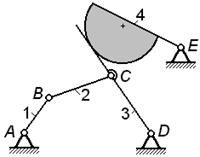
Задачи 25 – 30

Если изображенная кинематическая цепь является структурной группой, указать ее класс и порядок (в противном случае объяснить, почему цепь не является группой).

Направляющая 1 в состав кинематической цепи не входит

---

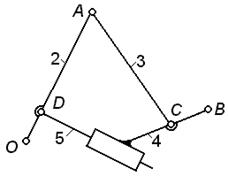
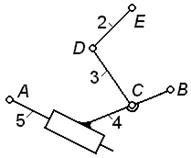
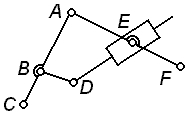
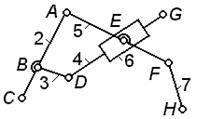
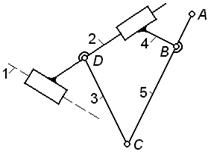
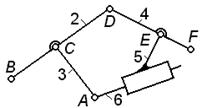
email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00