Главная
Лекция 5. Динамика
машин и механизмов.
Общие положения
Динамика - раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил. Имеется такое определение: “Динамика рассматривает силы в качестве причины движения тел”. В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует:
Из первого закона: Если равнодействующая всех внешних сил, действующих на механическую систему равно нулю, то система находится в состоянии покоя.
Из второго закона: Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы.
Из этих же законов следует, что динамическими параметрами механической системы являются:
- инерциальные (массы m и моменты инерции I);
- силовые (силы Fij и моменты сил Mij);
-
кинематические (линейные a и угловые 
ускорения).
В общей постановке динамика - изучение каких-либо процессов или явлений в функции времени.
Динамическая модель - модель системы, предназначенная для исследования ее свойств в функции времени (или модель системы, предназначенная для исследования в ней динамических явлений).
Прямая задача динамики - определение закона движения системы при заданном управляющем силовом воздействии.
Обратная задача динамики - определение требуемого управляющего силового воздействия, обеспечивающего заданный закон движения системы.
Методы
составления уравнений (динамической модели системы):
- энергетический (уравнения энергетического равновесия - закон сохранения энергия);
- кинетостатический (уравнения силового равновесия с учетом сил инерции по принципу Д’Аламбера).
Задачами динамического анализа и синтеза механизма, машины являются изучение режимов движения с учетом действия внешних сил и установление способов, обеспечивающих заданные режимы движения. При этом могут определяться мощности, необходимые для обеспечения заданного режима движения машины, проводиться сравнительная оценка механизмов с учетом их механического коэффициента полезного действия, устанавливаться законы движения ведущего звена (например, колебания угловой скорости кривошипа за один оборот) под действием внешних сил, приложенных к звеньям механизма, а также решаться задачи подбора оптимальных соотношений между силами, массами, размерами звеньев механизмов.
В динамике машин объектом изучения (исследования) является машинный агрегат. В общем виде его можно представить как механическую систему, состоящую из трех основных частей (рис. 4.1): машина-двигатель, передаточный механизм и рабочая машина (или исполнительный механизм). В ряде случаев в состав машинного агрегата входит система управления.
Рис. 5.1. Составные части машинного агрегата
В машине-двигателе какой-либо вид энергии преобразуется в механическую энергию, необходимую для приведения в движение рабочей машины. Например, в электродвигателе электрическая энергия преобразуется в механическую, а в двигателе внутреннего сгорания в механическую энергию преобразуется тепловая энергия сгорания топлива.
Передаточный механизм служит для преобразования движения, изменения характера движения, скорости, направления движения и т.д.
Рабочая машина предназначена для выполнения работы, связанной с трудовой деятельностью человека или выполнением технологического процесса.
Работа – физическая величина, характеризующая преобразование энергии из одной формы в другую.
Элементарная
работа силы выражается формулой
где Р – сила; dS – элементарная величина перемещения точки
приложения силы; 
– угол между векторами силы и скорости.
Элементарная работа момента силы выражается формулой
,
где М – момент силы; 
– элементарный угол поворота.
Размерность работы измеряется в джоулях: Дж = Нм.
Полная работа выражается формулами
, или 
.
Мощность – это энергетическая характеристика, равная отношению работы к интервалу времени ее совершения, выражается формулами
,
где V – скорость точки приложения силы Р,
или 
,
где 
– угловая скорость звена, к которому приложен момент.
Размерность мощности измеряется в ваттах: Вт = Дж/c; 1000 Вт =1 кВт (киловатт), 1 кВт = 1,
Кинетическая энергия,
приведенная масса, приведенный момент инерции механизма
Анализ движения машинного агрегата, находящегося под действием приложенных к нему внешних сил, удобно проводить с использованием метода приведения масс и сил к какому-либо звену механизма. Он сводится к анализу динамики тела (звена приведения), к которому приведены все внешние силы и моменты. Чаще всего звеном приведения выступает ведущее звено механизма.
Задача динамического анализа – определение истинного закона движения ведущего звена механизма, находящегося под действием заданных внешних сил и моментов, действующих в машинном агрегате.
Кинетическая энергия механизма
Для i-го звена, совершающего сложное движение (например, для шатуна кривошипно-ползунного механизма), кинетическую энергию можно выразить формулой
,
где первое
слагаемое правой части – это кинетическая энергия поступательного движения
центра масс звена; второе слагаемое – кинетическая энергия вращательного
движения; mi – масса звена; Vsi – скорость центра
масс; Jsi –
момент инерции звена относительно центра масс; 
– угловая скорость
звена.
Для всего механизма кинетическая энергия равна сумме кинетических энергий всех звеньев механизма:
(1)
где n – количество подвижных звеньев.
Приведенная масса механизма
Условно заменим механизм его динамической моделью. Например, кривошипно-ползунный механизм (рис. 4.2) заменим динамической моделью, состоящей из стойки и кривошипа.
Рис. 5.2. Замена кривошипно-ползунного механизма динамической моделью
Здесь ОА – звено приведения механизма, в котором как бы сосредоточена инертность всех звеньев механизма, А – точка приведения.
Уравнение (1) умножим и разделим на квадрат скорости точки приведения VA:
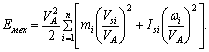
Выражение в квадратных скобках имеет
размерность массы (кг) и называется приведенной массой mпр
механизма в точке А.
Тогда
где
. (2)
Приведенной массой механизма называется такая условная масса, которая как бы сосредоточена в точке приведения механизма, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.
Приведенный момент инерции
Так как 
, где 
– длина звена приведения, 
– его угловая
скорость, то кинетическую энергию механизма можно выразить уравнением
где приведенный момент инерции механизма
.
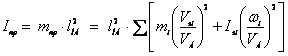(3)
Приведенным моментом инерции механизма называется такой условный момент инерции, которым как бы обладает звено приведения относительно оси вращения, кинетическая энергия которого (при таком моменте инерции) равна сумме кинетических энергий всех звеньев механизма.
Величины mпр и Jпр не являются постоянными для данного механизма, а меняют свое численное значение в зависимости от положений звеньев, так как звенья меняют свои скорости.
Пример 1.
Определить
приведенную массу и приведенный момент инерции для заданного положения
кривошипно-ползунного механизма (рис. 5.3), если известны положения центров
масс звеньев (S1 и S2),
линейные и угловые скорости звеньев и центров масс звеньев: 
, 
и 
– скорости центров масс
кривошипа, шатуна и ползуна, 
и 
– угловые скорости кривошипа и шатуна.
Рис. 5.3. Кривошипно-ползунный механизм
Пусть кривошип 1 – звено приведения, А – точка приведения.
Приведенная масса механизма согласно (4.2) вычисляется по формуле
,
а приведенный момент инерции согласно (3) – по формуле
.
Уравнение движения
машины в форме кинетической энергии
Рассмотрим
состояние механизма при двух различных положениях ведущего звена, разделяемых
каким-либо промежутком времени 
или углом поворота ведущего звена – кривошипа (рис.
5.4).
Рис. 5.4. Кинематические и динамические параметры механизма
при различных положениях звена приведения
При положении
кривошипа 
угловая скорость звена
приведения – 
, Iпр.0 – приведенный момент
инерции механизма в рассматриваемом положении.
При положении 
угловая скорость звена
приведения – 
, Iпр.1 – приведенный момент
инерции механизма.
Изменение
кинетической энергии механизма 
за этот промежуток
времени будет равно разности работ сил движущих Адв и сил
сопротивления Асопр, выполненных за
это время (или избыточной работе 
):
. (4)
(5)
где Е0 и Е1 – величины кинетических
энергий механизма при положениях и 
кривошипа.
(6)
(7)
где Мдв и Мсопр – приведенные моменты сил движущих и сил сопротивлений.
Подставив (5-7) в (4), получим
. (8)
Из (8) выразим
угловую скорость кривошипа при положении 
:
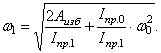(9)
Уравнение (9) называют уравнением движения машины в форме кинетической энергии.
Уравнение движения машины в дифференциальной форме
Уравнение (8) можно записать в виде
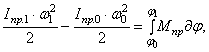(10)
где 
– суммарный
приведенный момент сил движущих и сил сопротивлений.
Продифференцируем
(10) по переменной 
:
(11)
Преобразуем 
, разделив числитель и знаменатель на
, и получим
,
где – угловое ускорение.
Тогда уравнение (11) можно записать в виде
Это есть дифференциальное уравнение движения машины для ведущего вращающегося ведущего звена.
Дифференциальное
уравнение движения машины для поступательно движущегося ведущего звена выводится
аналогично предыдущим выкладкам и имеет вид 
.
Решать дифференциальные уравнения движения можно графическим или численным методом (методом последовательных приближений).
Режимы движения машины
В общем виде движения машины можно разделить на три основных режима (периода): разгон, установившееся движение и останов (рис. 5.5).
Рис. 5.5. Схема режимов движения машины
В режиме разгона угловая скорость в начале режима 
, в
конце – 
, что следует из уравнения (4.9). При этом всегда 
, иначе разгон невозможен.
В режиме
установившегося движения 
,
изменение кинетической энергии (в среднем за один оборот ведущего вала) 
. В
пределах одного оборота происходят периодические колебания угловой скорости
вала машины.
В режиме
останова (когда двигатель отключен) 
. При этом выполняется работа, затрачиваемая на преодоление
сил трения: 
Механический кпд механизма
В период установившегося движения машины соблюдается условие равенства работ сил движущих и сил сопротивлений:
.
Работа сил
сопротивления складывается из суммы работ сил полезного сопротивления 
и сил вредного сопротивления
. Тогда
.
Разделим левую и правую части равенства на величину работы сил движущих:
и получим
где 
–
механический (цикловой) коэффициент полезного действия (кпд); 
– коэффициент механических потерь.
Определение
кпд машинного агрегата при последовательном соединении входящих в него
механизмов
Рассмотрим машинный агрегат, состоящий из последовательно соединенных механизмов, условно обозначенных на схеме (рис. 5.6) цифрами 1, 2 и 3.
А А1 А2 А3
Рис. 5.6. Машинный агрегат с последовательно соединенными механизмами
Пусть к механизму 1 подводится работа величиной А. На выходе получаем работу величиной А1, которая подводится к механизму 2 и т.д. Величина работы на выходе всегда меньше, чем подведенная работа на входе (А1<A, A2<A1, A3<A2), так как в каждом механизме имеются механические потери подведенной к нему работы.
Тогда общий кпд машинного агрегата
а кпд каждого механизма
, 
, 
.
Перемножим кпд всех последовательно соединенных механизмов:
Вывод: общий механический кпд машинного агрегата,
состоящего из последовательно соединенных n механизмов,
равен произведению их кпд:
Определение
кпд машинного агрегата при параллельном соединении входящих в него механизмов
Рассмотрим
машинный агрегат, состоящий из трех параллельно соединенных механизмов, условно
обозначенных на схеме (рис. 5.7) цифрами 1, 2, 3. Пусть к механизмам подводится
работа величиной А,
которая распределяется на каждый механизм в разных долях, определяемых
коэффициентами 
, 
, 
, каждый из которых меньше 1, а их сумма 
.
Рис. 5.7. Машинный агрегат с параллельно соединенными механизмами
Общий кпд всего машинного агрегата можно выразить отношением суммы работ на выходе механизмов к общей подведенной работе А:
. (12)
Так как
, 
;
, 
;
, 
,
то, подставив эти выражения в (12), получаем
.
Отсюда следует, что общий механический кпд машинного агрегата при параллельном соединении механизмов равен сумме величин кпд каждого механизма, умноженных на коэффициенты долей работ, подводимых к механизмам:
.
Сравним варианты последовательного и параллельного соединения механизмов с точки зрения минимизации механических потерь в машинном агрегате.
Пусть величины
кпд каждого механизма равны 
. При
этом коэффициенты, учитывающие доли распределения общей работы А между всеми механизмами,
также равны:
.
Тогда
, 
.
Так как 
, то 
. Отсюда следует, что параллельное соединение механизмов в
машинном агрегате предпочтительнее с точки зрения уменьшения механических
потерь.
Самоторможение
Если 
, то действительного движения механизма произойти не может.
Это называется явлением самоторможения. Следовательно, если при теоретических
расчетах получим 
, то механизм в заданном направлении двигаться не может.
Для возможности движения механизма необходимо обеспечить условие
.
Неравномерность хода ведущего звена машины
Уравнение движения главного вала машины в форме кинетической энергии имеет вид (см. формулу 9)
.
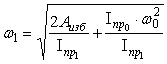Так как
величина избыточной работы 
, являясь функцией угла поворота вала , угловой скорости и времени t, есть величина переменная, т.е. 
, при этом 
, то при установившемся
режиме работы машины угловые скорости в начале и конце одного цикла Т (например, одного оборота) равны: 
(рис. 5.8).
За цикл
изменение кинетической энергии равно нулю 
. Внутри цикла угловая скорость вала может меняться, что вызывает
дополнительные динамические (инерционные) нагрузки, а также дополнительное
трение в кинематических парах, снижающее надежность механизма и его кпд.
Ухудшаются
условия работы механизма, приходится увеличивать материалоемкость машины,
повышать прочность звеньев, нести дополнительные энергетические затраты на
преодоление трения.
Рис. 5.8. Периодические колебания
угловой скорости главного вала машины в период установившегося движения
Коэффициент
неравномерности хода ведущего вала машины 
выразим формулой
, (13)
где
. (14)
Из (13) и (14)
получим
Величина может находиться в
следующих пределах: для ударных машин и прессов 
, для металлорежущих станков 
, для двигателей 
.
Регулирование
периодических колебаний угловой скорости с помощью маховика
В случае необеспечения требуемой величины при работе машины
могут возникнуть нежелательные явления и процессы (вибрация, повышенные
энергетические затраты, невозможность выполнения технологического процесса и
т.д.). При условии периодических колебаний угловой скорости вала для получения
заданной величины используют маховик –
массивное колесо с большим моментом инерции.
Основная
задача при расчете маховика – это определение его момента инерции. Маховик с
таким моментом инерции 
в интервале скоростей от 
до 
(см. рис.5.5) должен
произвести работу, равную изменению кинетической энергии механизма за это время:
.
Расчет величины момента инерции
маховика
Приведенный
момент инерции механизма можно представить в виде
при 
,
при 
,
где 
– постоянная составляющая приведенного момента инерции
механизма; – момент инерции
маховика или маховых масс (колес, валов и т.д.), (величина постоянная для
данного механизма); 
– составляющая приведенного момента инерции при максимальной
скорости в цикле ; 
– составляющая приведенного момента инерции при минимальной
скорости в цикле .
Тогда
.
(15)
Из (15) следует (если 
, 
.
С учетом (13) и (14) получим
. (16)
Для
определения величины задаются величинами 
и . Формулу (16) можно упростить, если принять 
. Тогда
.
При больших
маховых массах (когда 
) можно приближенно принять
.
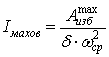Для
определения величины 
можно
пользоваться диаграммами моментов сил движущих 
и сил сопротивлений 
(рис. 5.9).
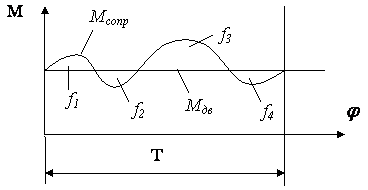
Рис. 5.9. Моменты сил движущих и сил
сопротивлений в цикле Т
Площади f1…f4,
ограниченные кривой Мсопр
и графиком Мдв,
представляют собой разности работ движущих моментов Мдв и моментов
сопротивлений Мсопр.
Суммы площадей имеют соотношение
Выбирают
наибольшую из заштрихованных площадей. Если 
, то величину максимальной
избыточной работы можно определить по формуле
,
где 
и 
– масштабы графиков по осям и М.
Регулирование непериодических колебаний скорости движения машин
В процессе выполнения работы приходится регулировать скорость рабочего органа машины. Например, в стационарных двигателях необходимо поддерживать скорость рабочего органа постоянной, а в двигателях транспортных машин эта скорость должна изменяться в широких пределах.
Из уравнения
движения машины следует, что изменения скорости рабочего органа можно
достигнуть за счет изменения разности работ движущих сил и сил сопротивления (
). Устройства, обеспечивающие изменения работы сил сопротивления
применяются в виде тормозов, например, в транспортных машинах, которые
снабжаются также и приспособлениями для одновременного разобщения двигателя с
машиной – орудием.
Другим способом регулирования является изменение работы движущих сил путем воздействия на орган, подающий энергию к входному звену (поршню у двигателя внутреннего сгорания, лопаткам турбины и т.д.).
Регулирование может осуществляться либо человеком-оператором, либо автоматически – с помощью устройств, называемых регуляторами.
Одним из них является центробежный регулятор (рис.5.10), приводимый во вращение валом двигателя В. Ползун А соединяется с органом, подводящим рабочее тело (пар, горючая смесь и т.д.). Регулятор автоматически поддерживает скорость вала двигателя постоянной, т.к. ее увеличение приводит к уменьшению подачи рабочего тела и наоборот.
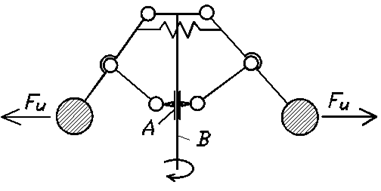
Рис.5.10
- Что изучается в разделе курса динамика машин и механизмов?
- Как формулируются прямая и обратная задачи динамики машин?
- Что называется "энергией", "работой" и "мощностью"?
- Как идеальные механизмы преобразуют энергию?
- Что называют коэффициентом полезного действия механической системы ?
- Как определяется КПД механической системы при последовательном и параллельном соединении элементов ?
- Какой режим движения машины называется установившимся ?
- Что называется "коэффициентом неравномерности" и какие величины этого коэффициента установлены для различных машин?
- Какими методами регулируется величина "коэффициента неравномерности" ?
- Как влияет момент инерции маховика на коэффициент неравномерности ?
- Как по коэффициенту неравномерности определяется необходимая маховая масса первой группы звеньев ?
- Изложите алгоритм решения задачи регулирования хода машины по методу Н.И. Мерцалова ?
- По каким зависимостям рассчитываются первые передаточные функции кривошипно-ползунного механизма ?
- Как определяются параметра динамической модели для двигателя внутреннего сгорания ?
- Как строится диаграмма кинетической энергии второй группы звеньев ?
- Как строится диаграмма угловой скорости звена приведения ?
- Как учитывается статическая характеристика асинхронного электродвигателя при анализе динамических процессов ?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов
