Главная

Тестовые вопросы по теме «Геометрические характеристики сложных плоских сечений»

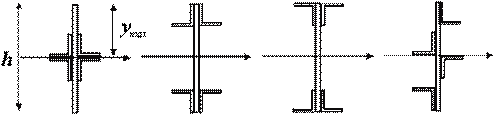
- Для балки из пластичного материала, какой формы сечение будет рациональным?

1) 2) 3) 4)

- Какая ось является центральной для данного сечения?

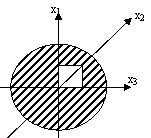
1. х₁;

2. х₂;

3. х₃.

- Определить знак центробежного момента инерции данного сечения.

1. ;

2. ;

3. .

- Момент инерции относительно оси x равен...

1. ;

2. ;

3. ;

4. .

- Чему равен ?

1. ;

2. ;

3. .

- Чему равен ?

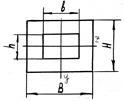
1. ;

2. ;

3. .

- Чему равен ?

1. ;

2. ;

3. .

- Определить на каком расстоянии друг от друга нужно расположить два швеллера №14, чтобы осевые моменты инерции сечения были равны между собой.

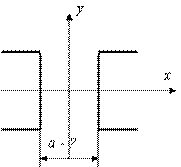
1. 4,63 см;

2. 20,4 см;

3. 7,35 см;

4. 16,0 см.

- Определить осевой момент инерции сечения относительно оси x.

1. 0,78а⁴;

2. 0,928а⁴;

3. 0,578а⁴;

4. 0,43а⁴

- Для сечения, составленного из двух неравнобоких уголков 100х63х10 определить момент инерции J_x .

1. 1059,4 см⁴;

2. 308 см⁴;

3. 483 см⁴;

4. 683 см⁴.

- Определить момент инерции сечения относительно центральной оси у_С.

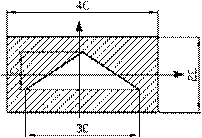
1.

2.

3.

4. .

- Определить на каком расстоянии друг от друга нужно расположить два двутавра №20, чтобы осевые моменты инерции сечения были равны между собой.

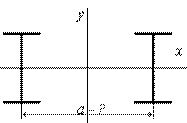
1. 20,2 см;

2. 16,04 см;

3. 12,24 см;

4. 32,24 см.

- Определить моменты инерции сечения относительно центральных осей х_С и у_С.

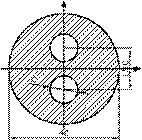
1.

2.

3.

4. .

- Рассчитать момент инерции сечения относительно оси у

1. 428·10⁴ мм⁴;

2. 572·10⁴ мм⁴;

3. 214·10⁴ мм⁴;

4. 286·10² мм⁴.

- Определить полярный момент инерции кольца, если осевой момент инерции равен I_x = 6 см⁴

1. 3 см⁴;

2. 6 см⁴;

3. 12 см⁴;

4. 18 см⁴.

- Определить координату х_с центра тяжести равнополочного уголка

1. 260 мм;

2. 198 мм;

3. 158,2 мм;

4. 210,2 мм.

- Выбрать формулу для расчета главного центрального момента инерции сечения относительно оси х

1. ;

2. ;

3. ;

4. .

- Определить координату у_с центра тяжести швеллера

1. 54 мм;

2. 114,4 мм;

3. 68,4 мм;

4. 94 мм.

- Выбрать формулу для определения осевого момента инерции сечения относительно его главной центральной оси y

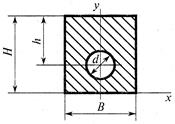
1. ;

2. ;

3. ;

4. .

- Рассчитать осевой момент относительно оси х

1. 3400·10³ мм⁴;

2. 900·10³ мм⁴;

3. 2500·10³ мм⁴;

4. 1600·10³ мм⁴.

- Определить полярный момент инерции сечения, если осевой момент инерции I_y = 15,5 см⁴

1. 11,6 см⁴;

2. 31 см⁴;

3. 15,5 см⁴;

4. 45,5 см⁴.

- Определить координату у_с двутавра

1. 150;

2. 110;

3. 180;

4. 135.

- Рассчитать осевой момент инерции равнополочного уголка 40×40×5 относительно оси х₁

1. 5,53 см⁴;

2. 10,73 см⁴;

3. 16,2 см⁴;

4. 23,34 см⁴.

- Рассчитать главный центральный момент инерции сечения I_x, если полярный момент инерции равен 248 см⁴

1. 496 см⁴;

2. 348 см⁴;

3. 248 см⁴;

4. 124 см⁴.

- Определить координату у_с центра тяжести швеллера.

1. 78 мм;

2. 93,4 мм;

3. 135,4 мм;

4. 104,6 мм.

- Выбрать формулу для расчета главного центрального момента инерции сечения относительно оси х

1. ;

2. ;

3. ;

4. .

- Определить координату y_c центра тяжести швеллера

1. 42 мм;

2. 58,7 мм;

3. 83,3 мм;

4. 141,3 мм.

- Рассчитать осевой момент инерции швеллера относительно оси х

1. 491 см⁴;

2. 537,6 см⁴;

3. 583 см⁴;

4. 1028 см⁴.

- Поперечное сечение образовано из трех жестко соединенных между собой профилей. Для одного уголка 11/7 имеем =172 см ⁴; =54,6 см⁴; =13,9 см²; остальные данные - на чертеже. Тогда главный центральный момент инерции относительно горизонтальной оси (Ou) будет равен в см⁴:

1. 492;

2. 542;

3. 592;

4. 642.

- Два швеллера N14 (А=15,6 см², J_x=491 см⁴, J_y=45,4 см⁴, b=58 мм. z₀=1,67 см.) жестко связаны между собой. Момент инерции сечения относительно оси y в cм⁴ равен:

1. 782;

2. 882;

3. 982;

4. 1082.

- Если поперечное сечение образовано из двух жестко соединенных друг с другом швеллеров N20 (I_x=1520 см⁴, I_у = 113 см^4,, А=23,4 см², b=76 мм и z₀=2,07 см), то момент инерции всего сечения относительно горизонтальной главной центральной оси (Оx) в см⁴ равен:

1. 1547;

2. 1657;

3. 1767;

4. 1877.

- Если поперечное сечение балки – это жестко соединенных между собой двутавра N30 (I_x=7080 см⁴; I_у=337 см⁴; A=46,5 см²; b=135 мм; d=6,5 мм), то главный центральный момент инерции сечения относительно горизонтальной оси Ou равен в cм⁴:

1. 10370;

2. 11520;

3. 12870;

4. 14120.

- Если поперечное сечение образовано двумя жестко связанными между собой швеллерами N14 (I_x=491 см⁴, I_у=45,4 см⁴, А=15,6 см², b=58 мм и z₀=2,67 см), то момент инерции всего сечения (I_u) относительно оси Ou в см⁴ равен:

1. 532;

2. 682;

3. 832;

4. 982.

- Если поперечное сечение – два жестко соединенных друг с другом двутавра N24 (А=34,8 см², I_x=3460 см⁴, I_у=198 см⁴, b=115 мм), то момент инерции всего сечения относительно оси Ou в см⁴ равен:

1. 1837;

2. 2185;

3. 2405;

4. 2697.

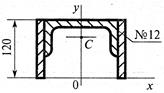
- Если поперечное сечение образовано из двух жестко соединенных друг с другом швеллеров N12 (I_x=304 см⁴, I_у=31,2 см⁴ , А=13,3 см2; z₀=1,54 мм), то момент инерции сечения относительно горизонтальной оси Ou в cм⁴ равен:

1. 126;

2. 146;

3. 166;

4. 186.

- Если поперечное сечение образовано из двух жестко соединенных друг с другом швеллеров N18 (I_x = 1090см⁴; I_y = 86см⁴; A = 20,7см²; b = 70 мм и z₀ = 1,94см), то момент инерции всего сечения относительно горизонтальной центральной оси Ou в см² равен:

1. 679;

2. 779;

3. 879;

4. 979.

- Для поперечного сечения, изображенного на чертеже, горизонтальная главная центральная ось располагается на расстоянии v_c равном в см:

1. 13,7;

2. 13,1;

3. 12,5;

4. 11,7.

Онлайн-калькулятор "Расчет геометрических характеристик кольцевого сечения"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин Теория машин и механизмов

00:00:00