Главная
Приведенный сборник задач предназначен для студентов всех форм обучения и включает в себя простейшие инженерные задачи, часто встречающиеся в рядовой практической работе. Необходимый справочный материал для решения задач даётся в их условиях. Для облегчения решения задач приведены готовые формулы и порядок их решения. Результаты решений всех задач находятся у преподавателя.
Большинство экзаменационных задач по курсам «Прикладная механика» и «Детали машин» составлены в вариациях на основе данного сборника. Успешное освоение решений приведенных задач даёт гарантированный шанс на получение положительной оценки при сдаче экзамена. Также данный сборник задач может быть весьма полезен начинающим инженерам-механикам в практической работе.
Задача 1
Определить полное удлинение жёстко заделанного круглого стержня от воздействия сил Р и напряжение растяжения в сечении стержня диаметром 0,8d. Принять следующие исходные данные: l=1м, d=0,02 м.
Модуль упругости материала стержня ![]() Мпа. Варианты
значений силы Р приведены в таблице.
Мпа. Варианты
значений силы Р приведены в таблице.
Задачу решить по одному из вариантов.
|
P,кН |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
2,2 |
2,4 |
2,6 |
3 |
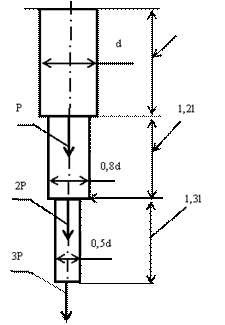
Порядок
решения:
Полное удлинение стержня по закону Гука
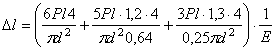 .
.
Напряжение в сечении стержня диаметром 0,8d
![]()
Задача 2
Определить необходимые диаметр и длину срезного пальца в, показанной
на рис., муфте предельного момента
исходя из следующих условий: диаметр D=200мм., количество пальцев n=4, допускаемое
напряжение среза материала пальца ![]() ср=100 Мпа., напряжение
смятия
ср=100 Мпа., напряжение
смятия ![]() см=200 Мпа.
см=200 Мпа.
Величина крутящего момента Т приведена в таблице. Задачу решить по одному из вариантов.
|
Т, Нм |
2000 |
2200 |
2400 |
2600 |
2800 |
3000 |
3200 |
3500 |
4000 |
4500 |
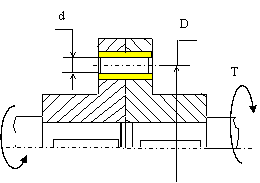
Порядок
решения:
Напряжение среза по сечению пальца ![]() , отсюда
, отсюда 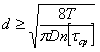 .
.
Напряжение смятия на поверхности пальца ![]() , где L - длина пальца.
, где L - длина пальца.
![]() .
.
Задача 3
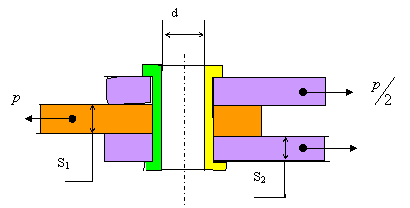
Определить внутренний диаметр заклёпки из условия её прочности на срез и проверить заклёпку на смятие.
Исходные данные: S1=S2=8 мм., диаметр заклёпки 15 мм., ![]() =120 Мпа,
=120 Мпа, ![]() =70 Мпа. Значение силы Р
приведено в таблице. Задачу решить по одному из вариантов.
=70 Мпа. Значение силы Р
приведено в таблице. Задачу решить по одному из вариантов.
|
P,кН |
10,5 |
11 |
11,5 |
12 |
12,5 |
13 |
13,5 |
14 |
14,5 |
15 |
Порядок
решения:
Напряжение среза в заклёпке ![]() (имеем две площадки среза),
(имеем две площадки среза),
отсюда
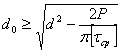 . Напряжение смятия в заклёпке
. Напряжение смятия в заклёпке ![]() .
.
Задача 4
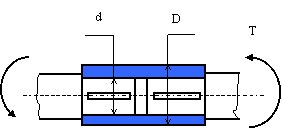
Определить
наименьший наружный диаметр глухой муфты при следующих исходных данных:
внутренний диаметр d =100 мм., допускаемое напряжение
на кручение материала муфты и шпонки ![]() =50 Мпа, внешний крутящий момент Т, запас прочности по крутящему моменту Кз=1,2.
Определить требуемую длину шпонки, если её ширина b=28 мм, высота h=16 мм, допускаемое напряжение смятия
=50 Мпа, внешний крутящий момент Т, запас прочности по крутящему моменту Кз=1,2.
Определить требуемую длину шпонки, если её ширина b=28 мм, высота h=16 мм, допускаемое напряжение смятия ![]() =200 Мпа. Ослаблением сечения муфты из-за шпоночного паза
пренебречь. Величина крутящего момента приведена в таблице. Задачу решить по
одному из вариантов.
=200 Мпа. Ослаблением сечения муфты из-за шпоночного паза
пренебречь. Величина крутящего момента приведена в таблице. Задачу решить по
одному из вариантов.
|
Т, Нм |
3000 |
3100 |
3200 |
3300 |
3400 |
3500 |
3600 |
3700 |
3800 |
3900 |
Порядок
решения:
Напряжение кручения в сечении муфты от действия крутящего момента
![]() ,
,
где ![]() - полярный момент сопротивления сечения без
учёта шпоночного паза. Решая, получим:
- полярный момент сопротивления сечения без
учёта шпоночного паза. Решая, получим:
![]() .
.
Длина
шпонки из условия смятия ![]() ,
,
Длина шпонки из условия среза ![]() .
.
Сечение стандартной шпонки ![]() мм.
мм.
Задача 5
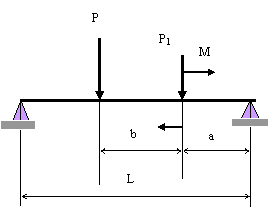
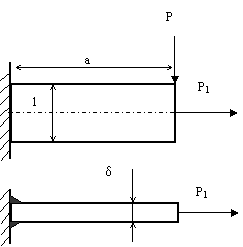
Круглый брус длиной L=1300 мм. Нагружен
силой Р=1000
Н и силой Р1 = 1500 Н.
Расстояние a= 300 мм, расстояние b =500
мм. Допускаемое напряжение изгиба материала бруса ![]() Мпа.
Определить диаметр стержня в месте приложения силы Р1 и момента М. Варианты величины момента М приведены в таблице. Задачу решить по
одному из вариантов.
Мпа.
Определить диаметр стержня в месте приложения силы Р1 и момента М. Варианты величины момента М приведены в таблице. Задачу решить по
одному из вариантов.
|
М, Нм |
800 |
900 |
1000 |
1100 |
1200 |
1300 |
1400 |
1500 |
1700 |
2000 |
Порядок
решения:
Напряжение изгиба бруса в сечении, где приложены сила Р1 и момент М.
![]() ,
, ![]() ;
;
![]() .
.
![]() .
.
Определяем большее
из этих значений ![]() ;
; ![]() .
.
Диаметр бруса
 .
.
Задача 6
Кронштейн
приварен к стенке двумя угловыми швами. На кронштейн воздействуют силы Р и Р1.
Определить необходимую величину катета сварного шва. Допускаемое напряжение в
сварном шве ![]() = 60 МПа. Определить толщину кронштейна
= 60 МПа. Определить толщину кронштейна ![]() из условия, что допускаемое напряжение
материала кронштейна
из условия, что допускаемое напряжение
материала кронштейна ![]() = 100
МПа. Значения сил Р и Р1 приведены в таблице. Задачу решить по одному
из вариантов.
= 100
МПа. Значения сил Р и Р1 приведены в таблице. Задачу решить по одному
из вариантов.
|
P, кН |
1 |
1,2 |
1,5 |
2 |
2,5 |
2,5 |
2,5 |
3 |
3,5 |
4 |
|
P1, кН |
0,8 |
1 |
1 |
1,5 |
1,5 |
2 |
2,5 |
2,5 |
2 |
2,5 |
Порядок
решения:
Суммарное напряжение в сварном шве ![]() ;
;
![]() ;
; ![]() ; где:
; где: ![]() - напряжение
от изгибающего момента (от силы Р),
- напряжение
от изгибающего момента (от силы Р), ![]() - напряжение
от силы Р1, k - искомый катет шва.
- напряжение
от силы Р1, k - искомый катет шва.
Толщина кронштейна определится из условия его прочности.
Суммарное напряжение в кронштейне ![]() ; отсюда
; отсюда
![]() .
.
Задача 7
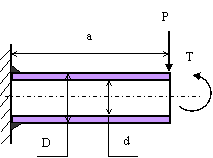
Труба наружным диаметром D=150 мм, и внутренним
диаметром d =150 мм приварена к вертикальной
стенке. Длина трубы
а = 300 мм. Труба нагружена
осевой силой Р=
10 кН и крутящим моментом Т. Определить величину катета, которым
необходимо приварить трубу, из условия, что допускаемое напряжение в сварном
шве ![]() Значения крутящего момента Т приведены в таблице. Задачу решить по одному
из вариантов таблицы.
Значения крутящего момента Т приведены в таблице. Задачу решить по одному
из вариантов таблицы.
|
Т, Нм |
5000 |
10000 |
15000 |
20000 |
25000 |
30000 |
35000 |
40000 |
45000 |
50000 |
Порядок
решения:
Суммарное напряжение в сварном шве возникает
от изгибающего момента, создаваемого силой Р, и от крутяшего
момента Т. Напряжения действуют во
взаимно перпендикулярных плоскостях , т. е. ![]() .
.
![]() - здесь
принято, что катет шва мал в сравнении с D и напряжения распределены равномерно по
кольцевой площадке диаметром D .
- здесь
принято, что катет шва мал в сравнении с D и напряжения распределены равномерно по
кольцевой площадке диаметром D .
![]() - здесь
принято, что
- здесь
принято, что ![]() .
.
Решая,
получим: ![]() .
.
Если труба приварена стыковым швом, то ![]() ;
; ![]() ;
;
![]() .
.
Задача 8
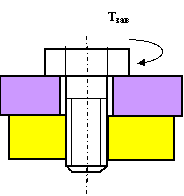
Определить силу, которую необходимо приложить к ключу длиной L при завинчивании болта по приведенному рисунку, до получения в теле болта напряжений, равных пределу текучести (т.е. когда срежется головка болта при его завинчивании). Предел текучести материала болта по напряжениям среза – 150 МПа. Диаметр болта – 16 мм. Варианты длины ключа приведены в таблице. Задачу решить по одному из вариантов.
|
L, мм |
150 |
200 |
250 |
300 |
350 |
400 |
450 |
500 |
500 |
600 |
Порядок
решения:
Напряжение среза в теле болта ![]() , Тзав = Рl , где Р - искомая сила.
, Тзав = Рl , где Р - искомая сила.
![]() -
полярный момент сопротивления сечения болта.
-
полярный момент сопротивления сечения болта.
Решая данные зависимости, получим ![]() .
.
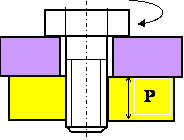
Задача 9
Определить силу, которую необходимо приложить
к ключу длиной 300 мм при завинчивании болта с резьбой М16![]() 2
по приведенному рисунку, до появления в резьбе болта напряжений смятия и
напряжений среза. Трением на торце болта пренебречь.
2
по приведенному рисунку, до появления в резьбе болта напряжений смятия и
напряжений среза. Трением на торце болта пренебречь.
Исходные данные: средний диаметр резьбы d2 = 15 мм,
предел текучести материала болта по напряжениям смятия ![]() =250 Мпа, по напряжениям среза
=250 Мпа, по напряжениям среза ![]() = 150 Мпа, коэффициент трения болта по гайке f= 0,15; угол профиля резьбы – 600, коэффициент
неравномерности распределения нагрузки по виткам резьбы k= 0,87; коэффициент
заполнения резьбы km= 0,65. Высота витка резьбы h= 1 мм. Высота гайки “H” приведена в таблице. Задачу решить по одному
из вариантов.
= 150 Мпа, коэффициент трения болта по гайке f= 0,15; угол профиля резьбы – 600, коэффициент
неравномерности распределения нагрузки по виткам резьбы k= 0,87; коэффициент
заполнения резьбы km= 0,65. Высота витка резьбы h= 1 мм. Высота гайки “H” приведена в таблице. Задачу решить по одному
из вариантов.
|
Н, мм |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
35 |
40 |
Порядок
решения:
Напряжение среза в резьбе болта ![]() ; напряжение смятия
; напряжение смятия ![]() .
.
где Р - осевая сила при затяжке болта, t - шаг резьбы.![]()
![]() ; где Тзав =Рзавl -
завинчивающий момент и Рзав - искомая сила.
; где Тзав =Рзавl -
завинчивающий момент и Рзав - искомая сила.
Решая, получим ![]() ;
;
![]() ;
;
![]() ;
; ![]() .
.
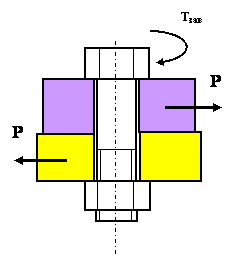
Задача 10
Определить завинчивающий момент, который
необходимо приложить к, показанному на рисунке болтовому соединению, чтобы
стягиваемые детали не разошлись от воздействия сил Р. Исходные данные: средний диаметр резьбы d2=15мм, угол
подъёма резьбы ![]() =
2,4310; угол трения в резьбе
=
2,4310; угол трения в резьбе ![]() =9,650;
коэффициент трения в резьбе f= 0,15. Трением на торце
гайки пренебречь. Значение силы Р приведено в
таблице.
=9,650;
коэффициент трения в резьбе f= 0,15. Трением на торце
гайки пренебречь. Значение силы Р приведено в
таблице.
|
Р, кН |
0,7 |
1 |
1,1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
Порядок
решения:
Необходимое усилие затягивания деталей ![]() ;
;
Момент, прилагаемый к болтовому соединению, для получения Рзат
![]() ; где
; где ![]() - угол
подъёма резьбы, t -шаг резьбы.
- угол
подъёма резьбы, t -шаг резьбы.
![]() - приведенный угол трения в резьбе.
- приведенный угол трения в резьбе.
Совместное решение: 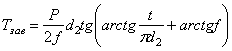 .
.
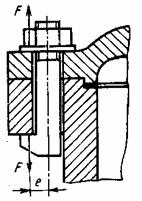
Задача 11
На рисунке показано крепление крышки
резервуара болтами с эксцентрично приложенной нагрузкой (болтами с костыльной
головкой). Болты затянуты силой F. Определить внутренний диаметр резьбы болта d из условия
растяжения и изгиба, принимая допускаемое напряжение растяжения ![]() = 100
МПа; величину e -эксцентриситета приложения нагрузки принять равной диаметру
болта.
= 100
МПа; величину e -эксцентриситета приложения нагрузки принять равной диаметру
болта.
Задачу решить по одному из вариантов.
|
F, кН |
1,5 |
1,8 |
2,0 |
2,2 |
2,4 |
2,6 |
2,8 |
3,0 |
3,2 |
3,4 |
Порядок
решения:
В приведенном на рисунке болте под действием
силы F возникают напряжения
растяжения равные ![]() и напряжения изгиба
и напряжения изгиба ![]() , где
, где ![]() - момент сопротивления стержня изгибу.
Эквивалентное напряжение в теле болта вычисляется по формуле
- момент сопротивления стержня изгибу.
Эквивалентное напряжение в теле болта вычисляется по формуле ![]() , где 1,3 –
коэффициент, учитывающий напряжение кручения при затяжке болта.
, где 1,3 –
коэффициент, учитывающий напряжение кручения при затяжке болта.
Отсюда искомый 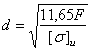 .
.
Задача 12
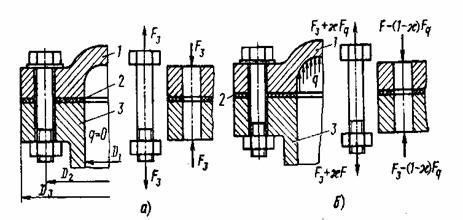
Определить усилие затяжки болтов крышки
резервуара из условия нераскрытия стыка, при
следующих исходных параметрах: - диаметр резервуара D1= 200 мм;
давление внутри резервуара постоянное ![]() (МПа); коэффициент запаса по затяжке k=1,5; коэффициент
внешней нагрузки
(МПа); коэффициент запаса по затяжке k=1,5; коэффициент
внешней нагрузки ![]() =0,5. Задачу решить по одному из вариантов.
=0,5. Задачу решить по одному из вариантов.
|
Х, МПа |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
Порядок
решения:
Для обеспечения нераскрытия
стыка сила, сжимающая детали в стыке всегда должна быть больше нуля. В данном
случае часть нагрузки от внутреннего давления, равная ![]() ,
дополнительно нагружает крепёжные болты, а остальная часть, равная
,
дополнительно нагружает крепёжные болты, а остальная часть, равная ![]() , идёт
на разгрузку стыка. Данное условие выражается в виде
, идёт
на разгрузку стыка. Данное условие выражается в виде ![]() .
Сила от внутреннего давления
.
Сила от внутреннего давления ![]() .
.
Задача 13
По рисунку и условиям задачи 12 определить диаметр болтов, стягивающих крышку и корпус резервуара, принимая количество болтов n = 8 шт и допускаемое напряжение на растяжение материала болтов равное 180 МПа. Задачу решить по одному из вариантов.
|
Х, МПа |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
Порядок
решения:
Для обеспечения нераскрытия
стыка сила, сжимающая детали в стыке всегда должна быть больше нуля. В данном
случае часть нагрузки от внутреннего давления, равная ![]() ,
дополнительно нагружает крепёжные болты, а остальная часть, равная
,
дополнительно нагружает крепёжные болты, а остальная часть, равная ![]() , идёт
на разгрузку стыка. Данное условие выражается в виде
, идёт
на разгрузку стыка. Данное условие выражается в виде ![]() . Сила от внутреннего давления
. Сила от внутреннего давления ![]() .
Осевая, растягивающая сила, действующая на затянутые болты равна
.
Осевая, растягивающая сила, действующая на затянутые болты равна ![]() .
.
Осевое растягивающее напряжение в сечении
болта ![]() .
.
Диаметр болта ![]()
Задача 14
По рисунку и условиям задачи 12 определить
напряжение среза ![]() в резьбе стягивающих болтов, принимая
количество болтов n =8 шт., коэффициент неравномерности
нагрузки по виткам резьбы K1=0,7 и коэффициент заполнения резьбы K= 0,87. Внутренний
диаметр резьбы болтов в зависимости от давления в резервуаре приведен в таблице. Высоту гайки
принять равной 0,7 от внутреннего диаметра резьбы болтов. Задачу решить по
одному из вариантов.
в резьбе стягивающих болтов, принимая
количество болтов n =8 шт., коэффициент неравномерности
нагрузки по виткам резьбы K1=0,7 и коэффициент заполнения резьбы K= 0,87. Внутренний
диаметр резьбы болтов в зависимости от давления в резервуаре приведен в таблице. Высоту гайки
принять равной 0,7 от внутреннего диаметра резьбы болтов. Задачу решить по
одному из вариантов.
|
Х, МПа |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
d, мм |
13,8 |
15,3 |
17,3 |
17,3 |
19,3 |
19,3 |
20,75 |
20,75 |
21,8 |
24,8 |
Порядок
решения:
Для обеспечения нераскрытия
стыка сила, сжимающая детали в стыке всегда должна быть больше нуля. В данном
случае часть нагрузки от внутреннего давления, равная ![]() ,
дополнительно нагружает крепёжные болты, а остальная часть, равная
,
дополнительно нагружает крепёжные болты, а остальная часть, равная ![]() , идёт на
разгрузку стыка. Данное условие выражается в виде
, идёт на
разгрузку стыка. Данное условие выражается в виде ![]() . Сила от внутреннего давления
. Сила от внутреннего давления ![]() . Осевая
растягивающая сила, действующая на затянутые болты равна
. Осевая
растягивающая сила, действующая на затянутые болты равна ![]() .
.
Напряжение среза в резьбе болта ![]() .
.
Задача 15
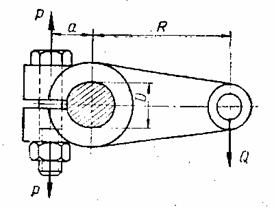
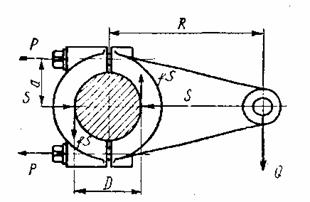
На рисунке показано клеммовое
крепление рычага на валу диаметром D =60 мм. Определить
диаметр внутренней резьбы двух болтов, стягивающих клеммовое
соединение, принимая силу Q =
2000 H, размер R=300 мм, размер a=50 мм. Коэффициент
трения между валом и рычагом f=0,12. Увеличение усилия
затягивания на деформацию рычага принять Кр=1,5
от требуемого усилия затягивания, дополнительную нагрузку на болты от
завинчивания гаек принять Кз=1,3
и коэффициент запаса по трению принять Кп=1,5.
Допускаемое напряжение в теле болтов от растяжения ![]() = 160
МПа.
= 160
МПа.
Порядок
решения:
Момент, создаваемый силой Q должен быть уравновешен моментом сил трения от действия силы затяжки болтов. Записав уравнение моментов с учётом условий задачи, получим необходимую силу затяжки болтов
![]() , где z - количество
болтов.
, где z - количество
болтов.
Отсюда внутренний диаметр резьбы болта:
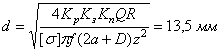
Задача 16
На рисунке показано клеммовое крепление рычага на валу диаметром D =60 мм. Определить необходимую силу затяжки болтов, стягивающих клеммовое соединение, принимая силу Q= 2000 H, размер R=500 мм, коэффициент трения по контакту рычага и вала f=0,12, коэффициент запаса по трению Kn=1.5. Определить контактное напряжение межу рычагом и валом, принимая ширину посадочной части рычага b=60 мм.
Порядок
решения:
Момент, создаваемый силой Q должен быть уравновешен моментом сил трения от действия силы затяжки болтов. Записав уравнение моментов с учётом условий задачи, получим необходимую силу затяжки болтов
![]() .
.
Контактное напряжение ![]() .
.
Задача 17
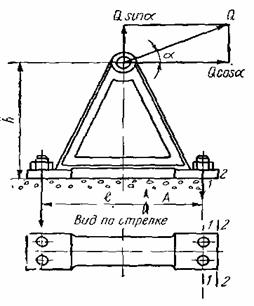
На рисунке показана стойка
опорного вала, на которую воздействует внешняя сила Q=4000 Н.
Определить необходимую силу затяжки P наиболее нагруженного
фундаментного болта, принимая коэффициент трения между стойкой и фундаментом f=0,2, размер l=500 мм, размер h=400 мм, Угол приложения силы Q к горизонту ![]() =300,
количество болтов z=4, коэффициент запаса по трению Kn=1,3.
=300,
количество болтов z=4, коэффициент запаса по трению Kn=1,3.
Порядок
решения:
Сила затяжки наиболее нагруженного болта определяется из уравнений равновесия внешних сил и моментов и сил трения от прижатия стойки к фундаменту.
![]()
Задача 18
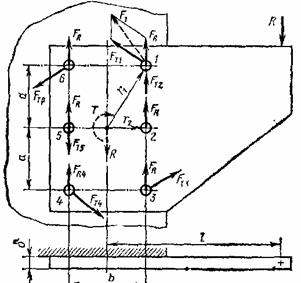
На
рисунке показан кронштейн, смонтированный на стойке с помощью болтов,
поставленных с зазором. Определить внутренний диаметр резьбы
наиболее нагруженного болта при следующих условиях: внешняя нагрузка R=5000 Н, Размер l=500мм, размер b= 150 мм, размер a= 150 мм, коэффициент
трения между подошвами кронштейна и стойки f=0,15, допускаемое
напряжение растяжения в теле болта ![]() = 100 Мпа,
коэффициент увеличения напряжения в теле болта от завинчивания гайки Kn=1.3. Коэффициент
запаса по затяжке К=1,5.
= 100 Мпа,
коэффициент увеличения напряжения в теле болта от завинчивания гайки Kn=1.3. Коэффициент
запаса по затяжке К=1,5.
Порядок
решения:
Внешняя сила R должна быть уравновешена силами трения от затяжки болтов. Составляя уравнение моментов, получим для данного случая
![]() .
.
![]() .
.
Нас интересует значение силы 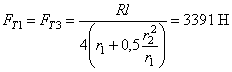
Необходимая сила затяжки болта ![]() .
.
Искомый внутренний диаметр резьбы болта ![]() .
.
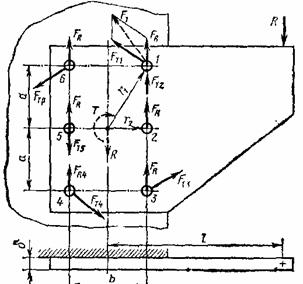
Задача 19
На
рисунке показан кронштейн, смонтированный на стойке с помощью шести заклёпок.
Определить диаметр наиболее нагруженной заклёпки при следующих условиях:
внешняя нагрузка R=5000 Н, Размер l=500 мм, размер b= 150 мм, размер a= 150 мм, допускаемое напряжение среза заклёпки ![]() = 60 Мпа. Определить
напряжение смятия не поверхности данной заклепки, принимая толщину кронштейна
= 60 Мпа. Определить
напряжение смятия не поверхности данной заклепки, принимая толщину кронштейна ![]() =15 мм.
=15 мм.
Порядок
решения:
Внешняя сила R должна быть уравновешена силами среза заклёпок. Составляя уравнение моментов, получим для данного случая
![]() .
.
![]() .
.
Нас интересует значение силы 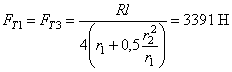 .
.
Искомый диаметр заклёпки ![]() .
.
Напряжение смятия ![]() .
.
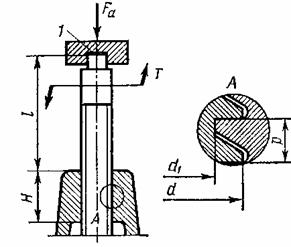
Задача 20
На рисунке схематично показан винтовой домкрат. Определить КПД домкрата; необходимую высоту гайки H и проверить винт на устойчивость при следующих исходных данных:
Резьба упорная 82х12, d1=64,2 мм, d2=76 мм, p=12 мм, высота профиля
витка h=9 мм,
грузоподъёмность Fa=150000 Н, коэффициент
трения в резьбе f=0,1, высота подъёма груза
L=1700 мм.
Допускаемое напряжение смятия в резьбе ![]() = 6 МПа. Модуль упругости материала винта
= 6 МПа. Модуль упругости материала винта ![]() МПа.
МПа.
Порядок
решения:
Коэффициент полезного действия винтовой пары вычисляется по формуле
![]() , где
, где ![]() - угол подъёма резьбы,
- угол подъёма резьбы,
![]() - угол трения в резьбе.
- угол трения в резьбе.
Минимальное число витков резьбы из условия
смятия ![]()
Высота гайки из условия смятия в резьбе ![]() мм.
мм.
Проверим винт на устойчивость по формуле
Эйлера ![]() ,
,
где
примем ![]() как для шарнирного закрепления концов стержня.
как для шарнирного закрепления концов стержня.
Формула справедлива при условии:
![]() , т.е.
>1600 мм, а у нас высота подъёма груза 1700 мм.
, т.е.
>1600 мм, а у нас высота подъёма груза 1700 мм.
![]() мм – момент инерции
сечения винта.
мм – момент инерции
сечения винта.
Вывод: винт по устойчивости не проходит. Необходимо уменьшить высоту подъёма груза или увеличить диметр резьбы.
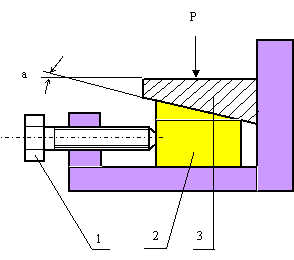
Задача 21
Определить
момент Тзав,
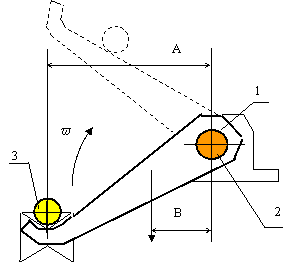
прикладываемый к винту поз.1, для подъёма детали поз.3, нагруженной силой Р, посредством перемещения клина поз.2.
Исходные данные: средний диаметр резьбы винта d2=15 мм, приведенный угол трения в резьбе ![]() =9,6480,
угол подъёма резьбы
=9,6480,
угол подъёма резьбы ![]() = 2,4310,
угол клина поз.2
а = 100,
коэффициент трения при перемещении клина по обеим поверхностям f=0,1. Трением на торце
винта и детали поз. 3 пренебречь. Значение силы Р приведено в таблице.
= 2,4310,
угол клина поз.2
а = 100,
коэффициент трения при перемещении клина по обеим поверхностям f=0,1. Трением на торце
винта и детали поз. 3 пренебречь. Значение силы Р приведено в таблице.
Задачу решить по одному из вариантов силы Р.
|
P, кН |
35 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
Порядок
решения:
Осевое усилие на винте для подъёма детали
поз.3 ![]() , где
, где
![]() - вертикальная сила, создаваемая при
перемещении клина поз.2,
- вертикальная сила, создаваемая при
перемещении клина поз.2,
![]() - угол трения в клине, Рf - сила трения между
клином поз.2 и корпусом,
- угол трения в клине, Рf - сила трения между
клином поз.2 и корпусом,
Росf - сила трения между деталью поз.3 и корпусом.
Момент, который необходимо приложить к винту поз.1 для получения силы Рос
![]() , где
, где ![]() - угол трения в резьбе,
- угол трения в резьбе, ![]() - угол
- угол
подъёма резьбы, t - шаг резьбы.
Окончательное решение 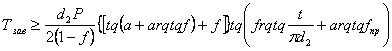 .
.
Задача 22
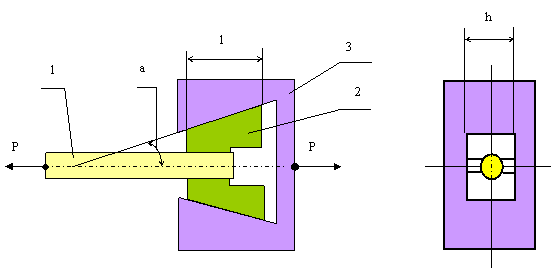
При исследовании механических характеристик материала, испытываемый образец 1 зажимается в клиновых плашках 2 клиновой головки 3 разрывной машины и подвергается растяжению силой Р.
Определить максимально возможный угол «a», при котором произойдёт самозаклинивание образца в плашках от силы растяжения, а также контактные напряжения между плашками и головкой.
Исходные данные:
коэффициент трения между плашками и образцом f1 =0,3.
- высота плашек h =100 мм.
- длина плашек l =100 мм.
Величина силы Р и коэффициента трения f2 между плашками и клиновой головкой приведены в таблице.
Задачу решить по одному из вариантов.
|
Р, кН |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
f2 |
0,16 |
0,15 |
0,14 |
0,13 |
0,12 |
0,11 |
0,1 |
0,09 |
0,08 |
0,06 |
Порядок
решения:
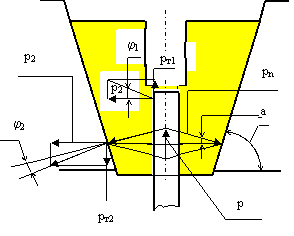
Сила
растяжения Р
передаётся на испытываемый пруток по контакту с плашками и на зажимную головку
по контакту с плашками. Из рисунка видно ![]() .
.
Контактное давление между плашкой и
головкой ![]() .
.
Условие самозаклинивания будет выполнено если сила трения между прутком и плашками будет
больше чем сила трения между плашками и головкой, т.е. ![]() .
. ![]() или
или ![]() ;
; ![]() - угол
трения между прутком и плашкой. Сила
трения Рт2
(см. рис.) с учётом угла клина "a"
- угол
трения между прутком и плашкой. Сила
трения Рт2
(см. рис.) с учётом угла клина "a" ![]() , где
, где ![]() - угол
трения между плашкой и головкой (
- угол
трения между плашкой и головкой (![]() ).
).
![]() или
или
![]() или
или ![]() .
.
![]() .
.
Задача 23
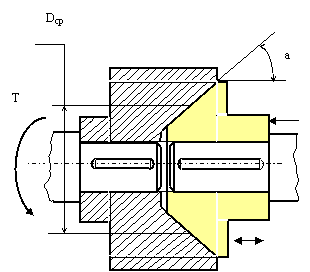
Определить силу Fa осевого прижатия простейшей конической муфты трения, необходимую для передачи крутящего момента Т = 100 МПа при среднем диаметре муфты Dср = 200 мм и коэффициенте трения между полумуфтами f = 0,1. Значение угла а приведено таблице. Задачу решить по одному из вариантов.
|
а, град |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
Порядок
решения:
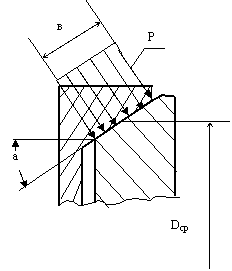
От действия силы Fa на конической
поверхности соприкосновения полумуфт возникает удельное давление Р и удельные
силы трения Рf.
Силы трения, направленные по касательной к окружности конуса, используются для
передачи крутящего момента. Рассматривая равновесие правой полумуфты
получим: ![]()
![]() , решаем
совместно
, решаем
совместно ![]() , здесь K - коэффициент запаса по трению.
, здесь K - коэффициент запаса по трению.
Минимально возможный угол конуса "a" должен быть больше угла трения материала полумуфт. Данная полумуфта не допускает смещения и перекоса соединяемых валов.
Задача 24
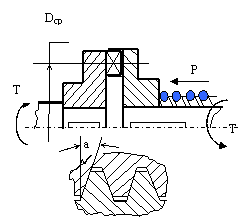
На рисунке упрощенно показана кулачковая муфта с пружинным прижимом одной полумуфты и профиль кулачков в зацеплении углом а. Определить максимальный крутящий момент, передаваемый муфтой при следующих исходных параметрах: коэффициент трения на поверхности кулачков f =0,1, угол а=300, трением полумуфты по поверхности вала пренебречь. Усилие прижима пружины Р приведено в таблице.
|
P, кН |
1 |
1,2 |
1,3 |
1,5 |
1,7 |
2 |
2,3 |
2,5 |
2,7 |
3 |
Порядок
решения:
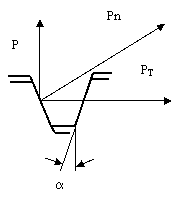
Осевая сила "Р" пружины на полумуфту создаёт окружную силу ![]()
Максимальный крутящий момент, передаваемый
полумуфтой ![]()
где![]() - угол
трения на кулачках муфты,
- угол
трения на кулачках муфты,
Kn = (0,8 - 0,9) - коэффициент неравномерности распределения нагрузки по кулачкам муфты. Результаты решения без учета коэффициента Kn.
Задача 25
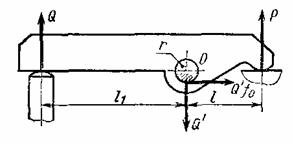
На рисунке схематично показан прихват детали к столу металлорежущего станка. Определить необходимую силу Q на штоке зажимного цилиндра при следующих условиях:
Сила прижима P=3000 Н, радиус поверхности штока r=10 мм, коэффициент трения на оси f0=0,1, размер l=50 мм, размер l1=150 мм. Определить контактное напряжение между прихватом и осью, принимая толщину прихвата s=15 мм.
Порядок
решения:
Сумма моментов относительно центра оси ![]()
Или ![]() , но
, но ![]() , тогда
, тогда
![]() ;
;
![]() ;
;
![]() ;
;
Из равенства следует![]()
Контактное напряжение ![]()
Задача 26
P
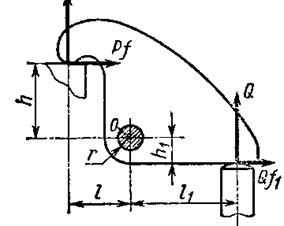
На рисунке схематично показан прихват детали к
столу металлорежущего станка. Определить необходимую силу Q зажимного
цилиндра при следующих условиях:
сила прижима P=3000 Н, радиус поверхности штока r=10 мм, коэффициент трения на оси f0=0,1, коэффициент трения между прижимом и деталью f=0,15, коэффициент трения между штоком цилиндра и прижимом f1=0,12, размер l=50 мм, размер l1=150 мм, размер h1=20 мм, размер h=35 мм. Определить контактное напряжение между прихватом и штоком, принимая толщину прихвата s=15 мм.
Порядок
решения:
Составив и решив уравнения равновесия моментов относительно точки О, получим:
![]() ,
,
Контактное напряжение ![]()
Задача 27
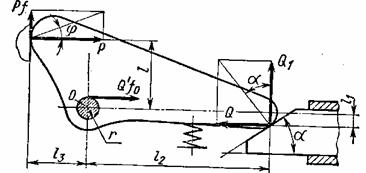
На рисунке схематично показан прихват детали
к столу металлорежущего станка. Определить необходимую силу Q зажимного плунжера со скошенной
поверхностью под углом ![]() =300
при следующих условиях: сила прижима P=3000 Н, радиус оси r=10 мм, коэффициент трения на оси f0=0,1,
коэффициент трения между прижимом и деталью f=0,15, коэффициент
трения между плунжером и прижимом f1=0,12,
размер l=50 мм, размер l1=15 мм,
размер l2=150 мм, размер l3=35 мм.
Определить контактное напряжение между прижимом и плунжером, принимая толщину
прихвата s=15 мм, радиус
контактной поверхности прижима R=20 мм и модуль упругости материала плунжера и прижима
=300
при следующих условиях: сила прижима P=3000 Н, радиус оси r=10 мм, коэффициент трения на оси f0=0,1,
коэффициент трения между прижимом и деталью f=0,15, коэффициент
трения между плунжером и прижимом f1=0,12,
размер l=50 мм, размер l1=15 мм,
размер l2=150 мм, размер l3=35 мм.
Определить контактное напряжение между прижимом и плунжером, принимая толщину
прихвата s=15 мм, радиус
контактной поверхности прижима R=20 мм и модуль упругости материала плунжера и прижима ![]() МПа.
МПа.
Порядок
решения:
Сумма моментов относительно оси:
![]() ;
;
![]() ;
;
![]()
![]() где
где ![]() – угол трения на зажимаемой поверхности.
– угол трения на зажимаемой поверхности.
Контактное напряжение по формуле Герца ![]()
Отсюда следует, что контактируемые поверхности должны быть закалены.
Задача 28
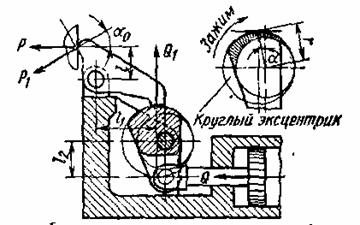
На рисунке схематично
показан прихват для зажима деталей с приводом от пневмоцилиндра
через эксцентриковый кулачёк с углом подъёма кривой ![]() =40.
Определить необходимую силу Q на штоке пневмоцилиндра при
следующих условиях: усилие прижима P1=3000 Н,
радиус кулачка r=50 мм, размер l=40 мм,
размер l1=60 мм, размер l2=50
мм, коэффициент трения на поверхности эксцентрика
=40.
Определить необходимую силу Q на штоке пневмоцилиндра при
следующих условиях: усилие прижима P1=3000 Н,
радиус кулачка r=50 мм, размер l=40 мм,
размер l1=60 мм, размер l2=50
мм, коэффициент трения на поверхности эксцентрика ![]() =0,12, коэффициент трения на оси эксцентрика
=0,12, коэффициент трения на оси эксцентрика ![]() =0,1,
коэффициент потерь от трения в зоне прижима принять
=0,1,
коэффициент потерь от трения в зоне прижима принять ![]() = 0,9,
угол отклонения силы P1
принять
= 0,9,
угол отклонения силы P1
принять ![]() = 150.
Определить контактное напряжение
между прижимом и кулачком, принимая толщину прижима s =
20 мм, радиус контактирующей поверхности кулачка r =50 мм, и модуль упругости
материала прижима и кулачка
= 150.
Определить контактное напряжение
между прижимом и кулачком, принимая толщину прижима s =
20 мм, радиус контактирующей поверхности кулачка r =50 мм, и модуль упругости
материала прижима и кулачка ![]() МПа.
МПа.
Порядок
решения:
Рассматривая кулачок как клин с углом подъёма 40 и, составляя уравнения равновесия сил и моментов, получим:
![]() ,
,
выражая силу через P1, будем иметь ![]() = 625 Н;
= 625 Н;
![]() = 2145 Н.
= 2145 Н.
Контактное напряжение по формуле Герца ![]()
Задача 29
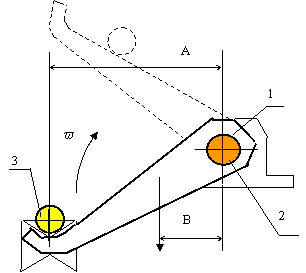
Рычаги 1, закреплённые на валу 2,
поворачиваются с угловой скоростью ![]() и снимают заготовку 3 с рольганга для передачи на технологическую обработку.
Определить мощность, необходимую для поворота вала 2 в подшипниках при следующих
известных параметрах:
и снимают заготовку 3 с рольганга для передачи на технологическую обработку.
Определить мощность, необходимую для поворота вала 2 в подшипниках при следующих
известных параметрах:
Масса заготовки - 100 кг.
Масса рычагов - 300 кг
Масса вала - 150 кг.
Диаметр стального вала - 0,1 м.
Размер А - 0,3 м.
Размер В до центра тяжести рычагов - 0,15 м.
Коэффициент трения в подшипниках - 0,1.
Варианты угловой скорости приведены в таблице.
|
|
3 |
2,7 |
2,5 |
2,2 |
2 |
1,9 |
1,8 |
1,6 |
1,3 |
1 |
Порядок
решения:
Мощность для поворота вала определится из
выражения ![]() , где М - крутящий момент, приложенный к валу,
, где М - крутящий момент, приложенный к валу,
![]() -
угловая скорость вала.
-
угловая скорость вала.
![]() , где mg - сила тяжести,
, где mg - сила тяжести,
![]() - момент трения в подшипниках вала.
- момент трения в подшипниках вала.
![]() .
.
Задача 30
Рычаги 1, закреплённые на валу 2,
поворачиваются с угловой скоростью ![]() и снимают заготовку 3 с рольганга для передачи на технологическую обработку.
Определить пусковую мощность, необходимую для поворота вала 2 в подшипниках при
следующих известных параметрах:
и снимают заготовку 3 с рольганга для передачи на технологическую обработку.
Определить пусковую мощность, необходимую для поворота вала 2 в подшипниках при
следующих известных параметрах:
Время поворота рычагов – 2 с.
Масса рычагов - 300 кг.
Масса вала- 150 кг.
Диаметр стального вала - 0,1 м.
Размер А - 0,3 м.
Размер В до центра тяжести рычагов- 0,15 м.
Коэффициент трения в подшипниках 0,1.
Масса заготовки и варианты угловой скорости приведены в таблице.
|
|
3 |
2,7 |
2,5 |
2,2 |
2 |
1,9 |
1,8 |
1,6 |
1,5 |
|
m, кг. |
100 |
120 |
140 |
150 |
160 |
180 |
200 |
220 |
250 |
Порядок
решения:
Пусковая мощность для поворота вала определится из выражения
![]() , где
, где ![]() - суммарный момент инерции составляющих
системы относительно оси вала,
- суммарный момент инерции составляющих
системы относительно оси вала,
![]() .
. ![]() -момент
инерции заготовки, m3g
-сила тяжести заготовки.
-момент
инерции заготовки, m3g
-сила тяжести заготовки.
Момент инерции вала относительно его
центра ![]() , где dm -масса тончайшего слоя вала,
, где dm -масса тончайшего слоя вала, ![]() -
радиус этого слоя, r - радиус вала.
-
радиус этого слоя, r - радиус вала.
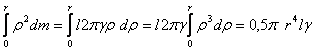 , здесь
, здесь ![]()
![]() ,
, ![]() - плотность материала вала, l - длина вала.
- плотность материала вала, l - длина вала.
Учитывая, что масса вала ![]() -
получим
-
получим ![]() .
.
![]() .
.
 Задача 31
Задача 31
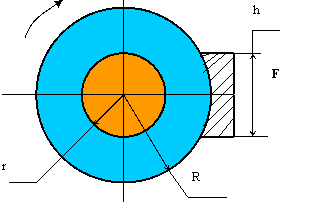 Маховое колесо кривошипных ножниц 1 вращается
на оси 2 с угловой скоростью
Маховое колесо кривошипных ножниц 1 вращается
на оси 2 с угловой скоростью ![]() . Радиус маховика R=0,4 м. Радиус оси r =0,075 м. Определить
сколько оборотов n сделает
колесо до полной остановки после прекращения действия внешнего крутящего
момента при следующих условиях:
. Радиус маховика R=0,4 м. Радиус оси r =0,075 м. Определить
сколько оборотов n сделает
колесо до полной остановки после прекращения действия внешнего крутящего
момента при следующих условиях:
Коэффициент трения между колесом и осью f = 0,05.
Сила на тормозе F = 0.
Величина угловой скорости в вариантах приведена в таблице.
Задачу решить по одному из вариантов.
|
|
1,57 |
2,093 |
2,617 |
3,14 |
3,66 |
4,187 |
4,71 |
5,23 |
5,76 |
6,28 |
Порядок
решения:
Кинетическая энергия вращения колеса должна
быть равна работе сил трения на его торможение, т.е. ![]() , где J - момент инерции колеса,
, где J - момент инерции колеса, ![]() - угол по ворота колеса до полной остановки.
- угол по ворота колеса до полной остановки.
Момент
трения - ![]() , где N - нормальная реакция силы веса колеса,
равная массе стального колеса m на ускорение силы тяжести - g, f -коэффициент трения между колесом и осью, r - радиус оси.
, где N - нормальная реакция силы веса колеса,
равная массе стального колеса m на ускорение силы тяжести - g, f -коэффициент трения между колесом и осью, r - радиус оси.
![]() .
.
Число оборотов ![]() .
.
Конечное решение ![]() .
.
 Задача 32
Задача 32
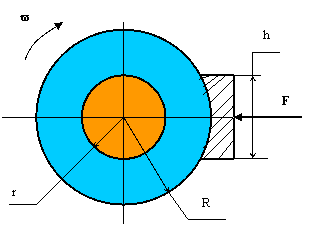 Маховое колесо кривошипных
ножниц 1 вращается на оси 2 с угловой
скоростью
Маховое колесо кривошипных
ножниц 1 вращается на оси 2 с угловой
скоростью ![]() . Радиус маховика R=0,4 м.
Радиус оси r=0,075 м.
Определить какую силу F необходимо приложить к тормозной
колодке, чтобы колесо совершило до полной остановки 0,2 оборота, а также
определить контактное напряжение между колодкой и колесом в момент приложения
данной силы.
. Радиус маховика R=0,4 м.
Радиус оси r=0,075 м.
Определить какую силу F необходимо приложить к тормозной
колодке, чтобы колесо совершило до полной остановки 0,2 оборота, а также
определить контактное напряжение между колодкой и колесом в момент приложения
данной силы.
Принять следующие исходные данные:
Масса колеса m = 280 кг. Ширина колеса -100 мм. Высота колодки h=250 мм. Ширина колодки l = 0,1 м. Коэффициент трения между колесом и осью f= 0,05. Коэффициент трения между колесом и колодкой f1 = 0,3. Величина угловой скорости приведена в таблице. Задачу решить по одному из вариантов таблицы.
|
|
1,57 |
2,093 |
2,617 |
3,14 |
3,66 |
4,187 |
4,71 |
5,23 |
5,76 |
6,28 |
Порядок
решения:
Кинетическая энергия вращения колеса должна
быть равна работе сил трения на его торможение, т.е. ![]() , где J - момент инерции колеса,
, где J - момент инерции колеса, ![]() - угол по ворота колеса до полной остановки.
- угол по ворота колеса до полной остановки.
Момент инерции колеса относительно оси
вращения вычисляется по формуле: ![]() .
.
Момент трения - ![]() , где N - нормальная реакция силы веса колеса,
равная массе стального колеса m на ускорение силы тяжести g, f
-коэффициент трения между колесом и осью,
f1 - коэффициент трения между колодкой тормоза и
колесом, r - радиус оси, число оборотов
, где N - нормальная реакция силы веса колеса,
равная массе стального колеса m на ускорение силы тяжести g, f
-коэффициент трения между колесом и осью,
f1 - коэффициент трения между колодкой тормоза и
колесом, r - радиус оси, число оборотов ![]() .
.
![]() .
.
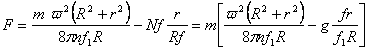
Контактное давление на поверхности колодки
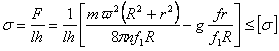 .
.
Задача 33
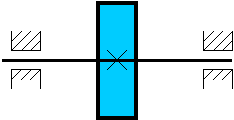
На вал диаметром d =100
мм и массой m =25 кг насажен маховик
диаметром D =400 мм и массой m1=100 кг. Валу сообщено вращение с частотой n =300 мин-1.
Определить время до полной остановки вала и угол поворота вала до полной
остановки после прекращения внешнего воздействия. Коэффициент трения в подшипниках f приведен в таблице.
Задачу решить
по одному из вариантов таблицы.
|
f |
0.005 |
0,01 |
0,02 |
0,03 |
0,04 |
0,06 |
0,07 |
0,08 |
0,1 |
0,12 |
Порядок
решения:
Момент сил трения в подшипниках можно
определить как реакцию от силы веса вала на коэффициент трения и плечо
трения, т. е. ![]() , где
, где
g - ускорение силы тяжести.
Время до полной остановки вала ![]() ;
; ![]() ;
;
![]() - угловое ускорение вала, которое можно
определить из условия, что момент сил трения в подшипниках равен вращающему
моменту вала:
- угловое ускорение вала, которое можно
определить из условия, что момент сил трения в подшипниках равен вращающему
моменту вала: ![]()
Суммарный момент инерции вала вместе с
маховиком ![]()
Решая уравнения, получим ![]() .
.
Задача 34
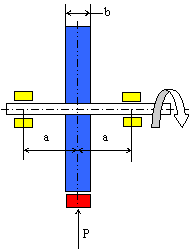
Вычислить максимальное касательное напряжение, возникающее в вале диаметром 65 мм при торможении, если вал с маховиком вращающийся со скоростью n= 1000 об/мин, после включения тормоза останавливается, сделав n1=5 оборотов. Момент инерции маховика J= 50кГм2. Силу торможения принять постоянной и движение вала равнозамедленным. Момент инерции вала не учитывать.
Порядок
решения:
По условиям задачи вращение вала в процессе
остановки является равнозамедленным. Начальная угловая скорость вала ![]() .
Конечная угловая скорость вала
.
Конечная угловая скорость вала ![]() .
.
Угловое ускорение вала ![]() ,
,
где ![]() – угол поворота вала по заданию.
– угол поворота вала по заданию.
Крутящий момент, приложенный к валу силами
инерции ![]() .
.
Напряжение кручения в сечениях вала,
нагруженных данным моментом
![]() , где
, где
![]() – полярный момент сопротивления сечения
вала.
– полярный момент сопротивления сечения
вала.
Задача 35
Вал с
маховиком, вращающийся со скоростью n=1000 об/мин, после включения тормоза останавливается, сделав n1=5 оборотов.
Вычислить диаметр вала, принимая максимальное касательное напряжение,
возникающее в вале при торможении, ![]() = 80
МПа. Момент инерции маховика J =
50 кГм2. Силу торможения
принять постоянной и движение вала равнозамедленным. Момент инерции вала
не учитывать.
= 80
МПа. Момент инерции маховика J =
50 кГм2. Силу торможения
принять постоянной и движение вала равнозамедленным. Момент инерции вала
не учитывать.
Вычислить силу торможения, принимая коэффициент трения между тормозной колодкой и маховиком f = 0,25.
Потерями на трение в подшипниках вала пренебречь.
Вычислить
контактное напряжение между колодкой тормоза и маховиком, принимая размер b=100 мм и высоту тормозной колодки 150 мм. Диаметр
маховика D= 300 мм.

Порядок
решения:
По условиям задачи вращение вала в процессе
остановки является равнозамедленным. Начальная угловая скорость вала ![]() . Конечная
угловая скорость вала
. Конечная
угловая скорость вала ![]() .
.
Угловое ускорение вала ![]() ,
,
где ![]() – угол поворота вала по заданию.
– угол поворота вала по заданию.
Крутящий момент, приложенный к валу силами
инерции ![]() .
.
Напряжение кручения в сечениях вала,
нагруженных данным моментом
![]()
Отсюда искомый диаметр вала

где ![]() – полярный момент сопротивления сечения вала.
– полярный момент сопротивления сечения вала.
Уравнение движения вала в период торможения
запишется в виде
![]() , т.е.
кинетическая энергия вращения вала будет затрачена на работу сил трения.
, т.е.
кинетическая энергия вращения вала будет затрачена на работу сил трения.
Момент сил трения ![]() .
.
Из совместного решения уравнений
![]()
Контактное напряжение на поверхности колодки
![]()
Задача 36
Вал с маховиком,
вращающийся со скоростью n= 1000 об/мин,
после включения тормоза останавливается, сделав n1=X оборотов. Вычислить
диаметр вала, принимая максимальное касательное напряжение, возникающее в вале
при торможении, ![]() = 80
МПа. Момент инерции маховика J= 50кГм2. Силу торможения
принять постоянной и движение вала равнозамедленным. Момент инерции вала
не учитывать. Вычислить силу торможения Р, принимая диаметр маховика D= 300 мм, коэффициент трения между
колодкой и маховиком f =
0,25. Потерями на трение в подшипниках вала пренебречь. Вычислить напряжение
изгиба в сечении вала под маховиком, принимая расстояние
а=100 мм.
= 80
МПа. Момент инерции маховика J= 50кГм2. Силу торможения
принять постоянной и движение вала равнозамедленным. Момент инерции вала
не учитывать. Вычислить силу торможения Р, принимая диаметр маховика D= 300 мм, коэффициент трения между
колодкой и маховиком f =
0,25. Потерями на трение в подшипниках вала пренебречь. Вычислить напряжение
изгиба в сечении вала под маховиком, принимая расстояние
а=100 мм.
|
X, об |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |

Порядок решения:
![]()
По условиям задачи вращение вала в процессе
остановки является равнозамедленным. Начальная угловая скорость вала ![]() . Конечная
угловая скорость вала
. Конечная
угловая скорость вала ![]() .
.
Угловое ускорение вала ![]() ,
,
где ![]() – угол поворота вала по заданию.
– угол поворота вала по заданию.
Крутящий момент, приложенный к валу силами
инерции ![]() .
.
Напряжение кручения в сечениях вала,
нагруженных данным моментом
![]()
Отсюда искомый диаметр вала

где ![]() – полярный момент сопротивления сечения вала.
– полярный момент сопротивления сечения вала.
Уравнение движения вала в период торможения
запишется в виде
![]() , т.е.
кинетическая энергия вращения вала будет затрачена на работу сил трения.
, т.е.
кинетическая энергия вращения вала будет затрачена на работу сил трения.
Момент сил трения ![]() .
.
Из совместного решения уравнений
![]()
Напряжение изгиба в сечении вала от действия
этой силы
![]()
Задача 37
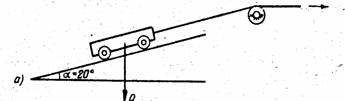
Вагонетка
с грузом движется по наклонному пути с постоянным ускорением а= 2 м/с2. Определить
требуемый диаметр, наматываемого на
приводной барабан троса, если масса вагонетки 4000 кг. Коэффициент трения
принять f=0,1. Массой троса пренебречь. Допускаемое напряжение растяжения для
троса ![]() = 60 Мпа.
= 60 Мпа.
Порядок
решения:
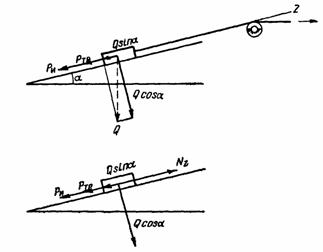
Сила инерции направлена в противоположную
сторону силе натяжения троса и равна ![]() ,
,
где ![]() - масса тележки,
- масса тележки,
![]() -
ускорение движения тележки.
-
ускорение движения тележки.
Сила трения при движении тележки
![]() .
.
Проецируем все силы на ось Z:
![]() .
.
Сила веса тележки ![]() , где
, где
g – ускорение свободного падения.
Окончательно получим
![]()
Напряжение растяжения в тросе ![]() , где А - площадь
сечения троса
, где А - площадь
сечения троса ![]() .
.
Отсюда диаметр троса
![]()
В знаменателе под корнем значение 106 – это перевод МПа в Па.
Задача 38
Вагонетка
с грузом трогается с места и движется по наклонному пути с постоянной скоростью
V=2 м/с. Время
разгона t=1 c. Определить пусковую и
статическую мощность привода, приняв коэффициент трения покоя f=0,15, коэффициент трения установившегося
движения f1=0,1, КПД всей
системы ![]() = 0,7.
Масса вагонетки 4000 кг. Момент инерции барабана вместе с тросом и валом Jпр = 30кГм2. Массой троса, наматываемого на барабан
пренебречь. Диаметр барабана 400мм.
= 0,7.
Масса вагонетки 4000 кг. Момент инерции барабана вместе с тросом и валом Jпр = 30кГм2. Массой троса, наматываемого на барабан
пренебречь. Диаметр барабана 400мм.
Рассчитать
требуемый диаметр троса в момент разгона, приняв допускаемое напряжение
растяжения для троса ![]() =60 Мпа.
=60 Мпа.

Порядок
решения:
Статическая мощность привода определится из
выражения ![]() , где
, где ![]() – сила натяжения каната при установившемся
движении; V –линейная скорость движения
тележки;
– сила натяжения каната при установившемся
движении; V –линейная скорость движения
тележки; ![]() - КПД системы.
- КПД системы.
![]()
![]()
Пусковая мощность привода сложится из
мощности, затрачиваемой на разгон тележки и мощности, затрачиваемой на разгон
вращающихся частей привода:
![]() ,
,
где V
- скорость на участке разгона максимальная
![]() - из решения
задачи №37
- из решения
задачи №37
![]() – ускорение
на участке разгона,
– ускорение
на участке разгона,
![]()
Угловая скорость барабана ![]() рад/с.
рад/с.
![]() – диаметр барабана.
– диаметр барабана.
![]()
Диаметр троса из условия максимальной силы на
участке разгона определится из выражения ![]()
Задача 39
Вагонетка
с грузом трогается с места и движется по наклонному пути с постоянной скоростью
V=2 м/с. Время разгона
t=1 c. Определить пусковую и
статическую мощность привода, приняв коэффициент трения покоя f=0,15, коэффициент трения установившегося
движения f1=0,1, КПД всей
системы ![]() =0,7.
Масса вагонетки 4000 кг. Момент инерции барабана вместе с тросом и валом Jпр = 30кГм2. Массой троса,
наматываемого на барабан пренебречь.
=0,7.
Масса вагонетки 4000 кг. Момент инерции барабана вместе с тросом и валом Jпр = 30кГм2. Массой троса,
наматываемого на барабан пренебречь.
Определить
минимальный диаметр вала, на котором посажен барабан, приняв диаметр барабана
400 мм, ширину барабана 600 мм, расстояние между опорами барабана 700 мм и
допускаемое напряжение на кручение материала вала ![]() =30 Мпа. Выбрать шарикоподшипники в опорах вала из расчёта на
10000 часов непрерывной работы.
=30 Мпа. Выбрать шарикоподшипники в опорах вала из расчёта на
10000 часов непрерывной работы.

Порядок
решения:
Из решения задачи №38 имеем силу натяжения троса Nz =26953Н.
Крутящий момент на валу барабана ![]()
Напряжение кручения вала ![]() ,
,
где ![]() полярный момент сопротивления сечения вала.
полярный момент сопротивления сечения вала.
Отсюда

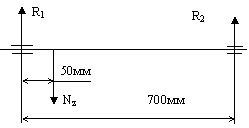
Для выбора подшипников определим максимальные
нагрузки. На рисунке приведена расчётная схема вала барабана, когда трос
находится на барабане в крайнем левом положении. В данном случае нагрузка на
левый подшипник составит ![]() Н.
Н.
Частота вращения вала ![]() , где
, где
V – скорость движения тележки, ![]() – диаметр
барабана.
– диаметр
барабана.
![]() об/мин.
об/мин.
Осевые нагрузки на подшипники отсутствуют и,
принимая коэффициент безопасности ![]() , получим
эквивалентную нагрузку на подшипник
, получим
эквивалентную нагрузку на подшипник ![]() Н.
Н.
Требуемая динамическая грузоподъёмность
подшипника определяется по известной зависимости
![]()
где - ![]() =10000
часов работы. Из каталога подшипников для данной грузоподъёмности может быть
предложен шарикоподшипник лёгкой серии №220, у которого динамическая
грузоподъёмность равна 124000 Н и внутренний диаметр 100 мм.
=10000
часов работы. Из каталога подшипников для данной грузоподъёмности может быть
предложен шарикоподшипник лёгкой серии №220, у которого динамическая
грузоподъёмность равна 124000 Н и внутренний диаметр 100 мм.
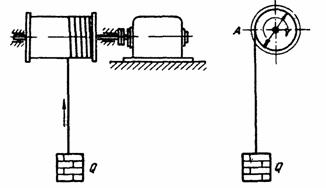
Задача 40
Движение барабана лебёдки в период пуска
выражается уравнением ![]() (
(![]() в
радианах, t в сек.) Вычислить напряжение в канате через одну секунду
после включения двигателя. Диаметр каната – 25 мм. Масса поднимаемого груза –
1500 кг. Массу каната не учитывать. Диаметр барабана – 800 мм.
в
радианах, t в сек.) Вычислить напряжение в канате через одну секунду
после включения двигателя. Диаметр каната – 25 мм. Масса поднимаемого груза –
1500 кг. Массу каната не учитывать. Диаметр барабана – 800 мм.
Порядок
решения:
Сила растяжения каната ![]() в период пуска будет складываться из силы веса
груза
в период пуска будет складываться из силы веса
груза ![]() (масса на ускорение свободного падения) и силы
инерции при разгоне
(масса на ускорение свободного падения) и силы
инерции при разгоне ![]() (масса на ускорение перемещения).
(масса на ускорение перемещения).
![]() Н.
Н.
Ускорение
a груза
должно быть равно ускорению каната в точке А
барабана, которое равно касательному ускорению при вращении барабана ![]() , где
, где ![]() - угловое ускорение барабана,
- угловое ускорение барабана, ![]() по условию задачи.
по условию задачи.
![]()
В конце первой секунды ускорение барабана ![]() 1/c2 и касательное ускорение в этот
момент
1/c2 и касательное ускорение в этот
момент
![]() .
.
Напряжение в канате ![]()
Задача 41
Вращение барабана лебёдки в период пуска
выполняется равноускоренно и через 2 сек. груз поднимается с постоянной
скоростью V = 1 м/с. Вычислить пусковую и статическую мощность
привода, принимая момент инерции привода, приведенный к валу барабана J = 50 Кгм2, диаметр барабана
800 мм. Определить максимальное напряжение
в канате. Диаметр каната – 25 мм. Масса поднимаемого груза – 1500 кг.
Массу каната не учитывать. КПД всей
системы принять ![]() = 0,75.
= 0,75.

Порядок
решения:
Сила растяжения каната ![]() в период пуска будет складываться из силы веса
груза
в период пуска будет складываться из силы веса
груза ![]() (масса на ускорение свободного падения) и силы
инерции при разгоне
(масса на ускорение свободного падения) и силы
инерции при разгоне ![]() (масса на ускорение перемещения).
(масса на ускорение перемещения).
Ускорение при подъёме груза ![]() .
.
Сила натяжения каната ![]()
Напряжение в канате ![]()
Статическая мощность привода определится из выражения
![]() , где
, где ![]() – сила натяжения каната при установившемся
движении;
– сила натяжения каната при установившемся
движении; ![]() – линейная
скорость движения груза;
– линейная
скорость движения груза; ![]() - КПД системы.
- КПД системы.
![]()
Пусковая мощность привода сложится из
мощности, затрачиваемой на подъём и разгон груза и мощности, затрачиваемой на
разгон вращающихся частей привода.
![]() , где
, где
V - скорость на участке разгона максимальная
Угловая скорость барабана ![]() рад/с.
рад/с.
![]() – диаметр барабана.
– диаметр барабана.
![]()
Задача 42
Определить длину l сварного соединения в нахлестку двух
стальных листов толщиной ![]() =5,0
мм, шириной а
= 100 мм, растягиваемых силами F = 25 кН.
=5,0
мм, шириной а
= 100 мм, растягиваемых силами F = 25 кН.
Порядок
решения:
При расчете предполагаем, что распределение
срезывающих сварку напряжений равномерное: ![]() , S –
площадь сечения среза.
, S –
площадь сечения среза.
Площадь сечения среза при наличии лобового и фланговых швов
![]()
Условие прочности сварочного соединения ![]() ,
,
где: ![]() – площадь среза лобового шва,
– площадь среза лобового шва, ![]() ,
,
![]() – длина шва
– длина шва
![]() – площадь среза фланговых швов,
– площадь среза фланговых швов, ![]() ,
,
![]() – длина флангового шва
– длина флангового шва
![]() ,
, ![]()
![]() , где
, где ![]()
Принимаем х = 20 мм
![]() мм.
мм.
Задача 43
Два стальных листа соединены заклепками.
Определить число заклепок, на срез ![]() = 80 МПа, диаметр заклепки dз = 8,0 мм, сила сдвига Q = 35 кН. Проверить
прочность заклепки смятие, если толщина листа h = 7,0 мм.
= 80 МПа, диаметр заклепки dз = 8,0 мм, сила сдвига Q = 35 кН. Проверить
прочность заклепки смятие, если толщина листа h = 7,0 мм.
Порядок
решения:
Из условия прочности на срез определяем поверхность среза
![]()
![]()
![]()
Определяем число заклепок n
![]()
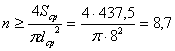
Принимаем число заклепок n = 9
Проверяем прочность заклепки на смятие
![]()
![]()
![]() 69 МПа < 160 МПа
69 МПа < 160 МПа
Условие прочности на смятие выполняется.
Задача 44
Рассчитать винт домкрата, а так же определить его КПД. Резьба самотормозящая упорная грузоподъемность Fа = 150 кН, l = 1,0 м, винт – сталь 35, гайка – чугун, подпятник – шариковый.
Порядок
решения:
1. Определим диаметр винта из условия износостойкости, приняв
![]() = 6
МПа,
= 6
МПа, ![]() = 1,8,
= 1,8, ![]() = 0,75
= 0,75
(![]() и
и ![]() ) –
коэффициент высоты гайки и резьбы.
) –
коэффициент высоты гайки и резьбы.
![]()
2. По таблицам стандарта выбираем резьбу х12:
d = 85 мм, р = 12 мм шаг резьбы
d1 = 64,2 мм, d2 = 76 мм, h = 9 мм (коэффициенты резьбы),
коэффициент трения ¦ = 0,1
Угол подъема резьбы
![]()
![]() , что
обеспечивает запас самоторможения.
, что
обеспечивает запас самоторможения.
3. Число витков: ![]()
![]() мм
мм
КПД домкрата (при наличии слабой смазки
в винте ¦
= 0,1)
![]()
Задача 45
Определить основные размеры цилиндрической
фрикционной передачи привода транспортера. Передаваемая мощность ![]() ,
, ![]() и
и ![]() угловые скорости ведущего и ведомого катков.
угловые скорости ведущего и ведомого катков.
Дано: Р = 1,5 кВ, ![]() = 90 с-1,
= 90 с-1,
![]() = 30 с-1.
= 30 с-1.
Порядок
решения:
Выбираем материалы катков: ведущий каток – текстолит ПТК, ведомого (большего) катка – чугун С4 – 18.
Передаточное число фрикционной передачи
![]()
Вращающий момент на ведущем валу
![]() Н/м
Н/м
Задаемся коэффициент ширины катка ![]() = 0,3,
коэффициент запаса сцепления k = 1,3.
= 0,3,
коэффициент запаса сцепления k = 1,3.
Допускаемое контактное напряжение для
текстолитовых катков ![]() = 100
МПа, коэффициент трения текстолита по чугуну ¦
= 0,3. Модули упругости текстолита
= 100
МПа, коэффициент трения текстолита по чугуну ¦
= 0,3. Модули упругости текстолита ![]() МПа, чугуна
МПа, чугуна ![]() МПа.
МПа.
Приведенный модуль упругости:
![]() МПа
МПа
Находим межосевое расстояние
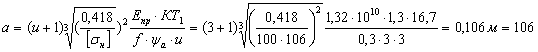 мм
мм
Определяем основные размеры катков:
диаметр ведущего катка ![]() мм
мм
диаметр ведущего катка ![]() мм
мм
ширина катков
![]() мм
мм
![]() мм.
мм.
Задача 46
Определить основные геометрические параметры
зубчатой цилиндрической косозубой пары по следующим исходным данным:
допускаемое контактное напряжение материала зубчатых колес ![]() = 410
МПа, крутящий момент на валу колеса Т2 =290 Нм, передаточное число зубчатой пары u =
4.
= 410
МПа, крутящий момент на валу колеса Т2 =290 Нм, передаточное число зубчатой пары u =
4.
Порядок
решения:
Примем коэффициент долговечности для
длительно работающей передачи ![]() =1,
коэффициент неравномерности нагрузки
=1,
коэффициент неравномерности нагрузки ![]() = 1,09,
коэффициент ширины зубчатого венца
= 1,09,
коэффициент ширины зубчатого венца ![]() = 0,4, примем
предварительно угол наклона зубьев
= 0,4, примем
предварительно угол наклона зубьев ![]() =100.
=100.
Из условия контактной прочности межосевое
расстояние равно
 .
.
Примем стандартное значение ![]() = 160 мм.
= 160 мм.
Нормальный модуль ![]() мм
мм
Примем стандартное значение m=2
мм.
Число зубьев шестерни
![]()
Число зубьев колеса ![]()
Фактический угол наклона зубьев
![]()
Угол ![]() =14024’
=14024’
Диаметры делительных окружностей
![]()
![]()
Диаметры окружностей вершин зубьев
![]()
![]()
Диаметры окружностей впадин
![]()
![]()
Ширина венца зубчатого колеса и шестерни
![]()
![]() ,
,
примем
![]()
Ответ: ![]() =160
мм, d1=64
мм, d2 =
256 мм, da1=68
мм, da2=260
мм, df1=59
мм, df2=251
мм, b1=70 мм, b2=64 мм, m=2 мм,
=160
мм, d1=64
мм, d2 =
256 мм, da1=68
мм, da2=260
мм, df1=59
мм, df2=251
мм, b1=70 мм, b2=64 мм, m=2 мм, ![]() =14024’.
=14024’.
Задача 47
Выполнить предварительный проектный расчет
вала зубчатого колеса по следующим исходным данным: крутящий момент на валу Т=290 Нм, материал вала - сталь 45,
допускаемое напряжение на кручение ![]() =(20…30)
МПа, вала ступенчатого типа.
=(20…30)
МПа, вала ступенчатого типа.
Порядок
решения:
1. Диаметр выходного конца вала определяем по крутящему моменту с учетом допускаемого напряжения на кручение
![]()
2. Диаметр вала под манжетой
![]() , примем dм=24
мм.
, примем dм=24
мм.
3. Диаметр вала под подшипниками
![]() .
.
Внутренние посадочные диаметры подшипников кратны пяти, поэтому принимаем диаметр вала dп=30 мм.
4. Диаметр вала под колесом
dк=dп+(4…6)=30+(4…6)=(34…36)
мм, принимаем dк=36 мм.
Задача 48
Определить минимальный диаметр приводного вала 1 электрической лебёдки из расчёта в период разгона. Масса поднимаемого груза m=500 кг; момент инерции барабана и других деталей, вращающихся вместе с ним относительно оси вала 2: J=30 Кгм2.
Моментом инерции вала 1 и посаженной на нём
шестерни пренебречь. КПД системы привода ![]() = 0,75.
Принять, что в период разгона вал 1 вращается равноускоренно и через 2 сек.
после включения приобретает рабочую скорость вращения nдвиг = 710 об/мин. Допускаемое
напряжение материала вала 1 при расчёте
по касательным напряжениям принять
= 0,75.
Принять, что в период разгона вал 1 вращается равноускоренно и через 2 сек.
после включения приобретает рабочую скорость вращения nдвиг = 710 об/мин. Допускаемое
напряжение материала вала 1 при расчёте
по касательным напряжениям принять ![]() = 30 Мпа.
= 30 Мпа.
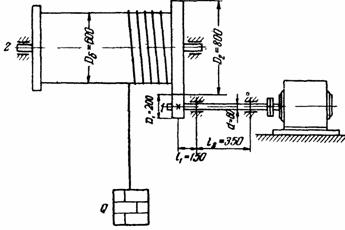
Порядок
решения:
Рабочая скорость подъёма груза ![]()
Мощность двигателя в пусковом режиме будет
складываться из мощности на подъём груза, мощности на разгон груза и мощности
на разгон вращающихся частей привода.
![]()
где ![]() м/с2 – ускорение при подъёме груза.
м/с2 – ускорение при подъёме груза.
![]() рад/с - угловая скорость барабана.
рад/с - угловая скорость барабана.
![]() – КПД системы привода по условиям задачи.
– КПД системы привода по условиям задачи.
![]() .
.
Крутящий момент на вале 1
![]() Нм.
Нм.
Диаметр вала из условия прочности на кручение
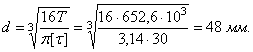
Задача 49
Рассчитать нагрузки на наиболее нагруженном подшипнике приводного вала 1 электрической лебёдки в период разгона. Выбрать подшипник и рассчитать его на 5000 часов работы.
Масса поднимаемого груза Q= 1000 кг; момент инерции барабана и других деталей,
вращающихся вместе с ним относительно оси вала 2: J=30 Кгм2.
Моментом инерции вала 1 и посаженной на нём шестерни пренебречь. Потери
мощности не учитывать. Принять, что в период разгона вал 1 вращается
равноускоренно и через 2 сек. после включения приобретает рабочую скорость
вращения n= 960 об/мин. Допускаемое
напряжение материала вала 1 при расчёте по максимальным касательным напряжениям
принять ![]() = 100 Мпа.
= 100 Мпа.

Порядок
решения:
В период разгона вал 2 передаёт момент, равный сумме трёх моментов:
а) статического сопротивления поднимаемого груза
![]() ;
;
б) момента, расходуемого на разгон груза до
заданной скорости ![]() ;
;
в) момента, расходуемого на разгон
вращающихся масс ![]() .
.
Таким образом, ![]() .
.
Ускорение поступательного движения груза связано с угловым ускорением барабана
зависимостью ![]() .
.
Угловое ускорение ![]() вала 2 выражается через угловое ускорение вала
1:
вала 2 выражается через угловое ускорение вала
1: ![]() .
.
Угловое ускорение ![]() вала 1 определяется из известного выражения
вала 1 определяется из известного выражения
![]() ;
; ![]() ;
; ![]() .
.
![]() .
.
Отсюда ![]() .
.
Окружная сила в зацеплении зубчатых колёс ![]() .
.
Радиальная сила в зацеплении ![]() .
.
(![]() - угол
зацепления равный 200)
- угол
зацепления равный 200)
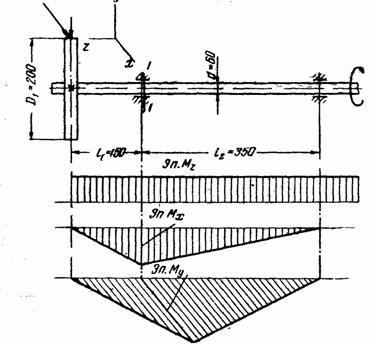
На рисунке показана расчётная схема вала 1 и
последовательно эпюры: крутящего момента от силы ![]() .
. ![]() ,
,
изгибающего момента от силы ![]() :
: ![]() ,
,
изгибающего момента от силы ![]() :
: ![]() .
.
Эквивалентный момент под наиболее нагруженной
опорой по гипотезе наибольших касательных напряжений
![]() .
.
Эквивалентное напряжение в сечении вала под
подшипником
![]() , где
, где ![]() -
-![]() момент
сопротивления сечения вала.
момент
сопротивления сечения вала.
Окончательно получим ![]() .
.
Суммарная нагрузка на левый подшипник 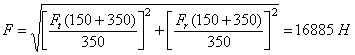 .
.
Требуемая
грузоподъёмность подшипника ![]()
По каталогу подшипников выбираем
роликоподшипник №7312, у которого динамическая грузоподъёмность 128000Н и
внутренний диаметр 60мм. (![]() =1,2 – коэффициент безопасности,
=1,2 – коэффициент безопасности, ![]() = 5000 ч – срок службы)
= 5000 ч – срок службы)
Задача 50
Стальной пруток 1 диаметром «d» протягивается через волоку 2 силой волочения «Рв» со скоростью «V». Определить скорость «отстрела» прутка в момент окончания волочения, принимая допущение, что потенциальная энергия его растяжения переходит в кинетическую энергию движения в направлении волочения. Учесть, что скорость "отстрела" складывается со скоростью волочения.
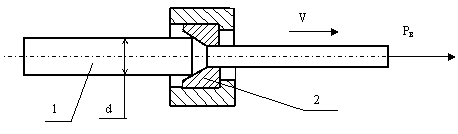
|
Исходные данные |
|||||||||
|
Рв, кН |
50 |
60 |
70 |
80 |
100 |
150 |
200 |
250 |
300 |
|
d, мм |
10 |
12 |
13 |
15 |
16 |
20 |
25 |
30 |
35 |
|
V , м/с |
1,7 |
1,7 |
1,6 |
1,6 |
1,5 |
1,5 |
1,2 |
1 |
1 |
Порядок
решения:
В соответствии с условиями задачи запишем,
что потенциальная энергия растяжения прутка силой волочения ![]() равна кинетической энергии его движения в
момент окончания процесса волочения:
равна кинетической энергии его движения в
момент окончания процесса волочения:
![]() или
или ![]() , где
, где ![]() - относительное удлинение прутка при волочении
по закону Гука
- относительное удлинение прутка при волочении
по закону Гука
Е - модуль упругости материала прутка,
А - площадь поперечного сечения материала прутка,
Vк - скорость движения, приобретаемая прутком при снятии нагрузки растяжения.
Решая уравнение, получим: ![]() ,
,
Где ![]() -
удельный вес (плотность) материала прутка равна 7,85 г/cм3.
-
удельный вес (плотность) материала прутка равна 7,85 г/cм3.
Полная
скорость ![]() .
.
Задача 51
Для разрушения старых зданий часто используют передвижной кран, на стреле которого подвешен стальной шар массой M. Oпределить диаметр проволоки каната, на котором подвешивается шар из следующих условий:
- длина каната L=5 м.
- число проволок в канате N
-запас прочности каната на разрыв Кз=6
-угол отклонения шара от вертикали 450.
-начальная скорость, сообщаемая шару V=1 м/c.
-допускаемое напряжение растяжения материала проволоки каната 600 Мпа.
|
M, кг |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
1100 |
|
N, шт |
48 |
48 |
64 |
64 |
80 |
96 |
112 |
128 |
144 |
160 |

Порядок
решения:
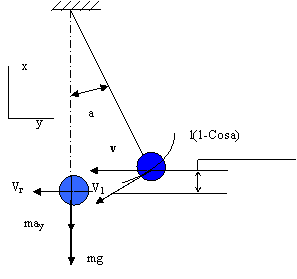
Диаметр проволоки определится из уравнения
прочности ![]() , т.е.
, т.е.![]() .
.
Сила натяжения каната определится из третьего
закона Ньютона ![]() (сумма проекций на ось Y в вертикальном положении каната).
(сумма проекций на ось Y в вертикальном положении каната).
![]() - центробежное ускорение,
- центробежное ускорение,
![]() - горизонтальная (окружная) скорость шара,
определяемая из условия сохранения энергии его движения
- горизонтальная (окружная) скорость шара,
определяемая из условия сохранения энергии его движения![]()
![]()
![]() ;
; ![]() ,
,
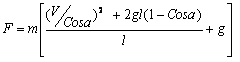 ,
,
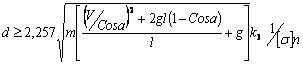
где g - ускорение силы тяжести.
Задача 52
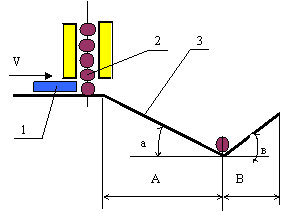
Дозатор
автоматической линии 1 отсекает один обрабатываемый ролик 2 и со
скоростью V
отправляет его в желоб 3 на
последующую обработку. Углы наклона желоба:
а = 150 , в =
450. Размер желоба А= 200 мм.
Определить минимальную длину желоба по размеру В,
при которой ролик по инерции не выкатится за пределы желоба и вернётся в его
центр. Принять скорость V= 0,5 м/с, коэффициент трения качения между
роликом и поверхностью желоба k=0,0002 м. Варианты диаметров ролика
приведены в таблице. Задачу решить по одному из вариантов.
|
d, мм |
10 |
12 |
15 |
18 |
20 |
22 |
25 |
30 |
35 |
40 |
Порядок
решения:
По закону сохранения энергии суммарная энергия ролика в нижней части желоба за вычетом работы сил трения на участке скатывания должна равняться работе подъёма ролика по крутой стенке желоба плюс работа сил трения на участке подъёма, т.е.
![]() ;
;
где ![]() - кинетическая энергия
ролика в начале движения,
- кинетическая энергия
ролика в начале движения,
![]() - потенциальная энергия ролика в начале
движения,
- потенциальная энергия ролика в начале
движения,
g - ускорение силы тяжести,
![]() - сила трения при скатывании ролика, d -диаметр ролика,
- сила трения при скатывании ролика, d -диаметр ролика,
![]() - сила трения при подъёме ролика, k - коэффициент трения.
- сила трения при подъёме ролика, k - коэффициент трения.
Общее решение уравнений 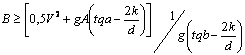
Задача 53
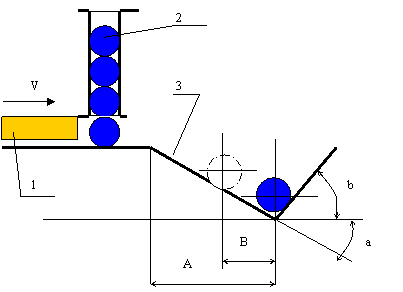
Дозатор
1 автоматической линии со скоростью V=0,5 м/с. отсекает один обрабатываемый ролик
2 и отправляет его в желоб 3 на последующую операцию. Углы наклона желоба а=150,
b=750.
Длина участка желоба А=0,2
м. После соударения со стенкой желоба ролик отскакивает на величину В=0,02 м. Определить контактное
напряжение между стенкой желоба и роликом в момент соударения из следующих
условий:
Ролик
и желоб - стальные. Длина ролика l = 50 мм. Коэффициент трения качения между роликом и желобом принять k=0,0002 м. Потерями на деформацию ролика и желоба в момент соударения -
пренебречь.
Модуль
упругости материала и его плотность
принять ![]() Мпа, и 7,8 г/см3.
Расчёт выполнить для одного из диаметров ролика, представленных в таблице.
Мпа, и 7,8 г/см3.
Расчёт выполнить для одного из диаметров ролика, представленных в таблице.
|
D,мм. |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
Порядок
решения:
Кинетическая энергия вращения колеса должна
быть равна работе сил трения на его торможение, т.е. ![]() , где J - момент инерции колеса,
, где J - момент инерции колеса, ![]() - угол по ворота колеса до полной остановки.
- угол по ворота колеса до полной остановки.
Момент
трения - ![]() , где N - нормальная реакция силы веса колеса,
равная массе стального колеса m на ускорение силы тяжести - g, f -коэффициент
трения между колесом и осью, r - радиус оси.
, где N - нормальная реакция силы веса колеса,
равная массе стального колеса m на ускорение силы тяжести - g, f -коэффициент
трения между колесом и осью, r - радиус оси.
![]() .
.
Число оборотов ![]() .
.
Конечное решение ![]() .
.
Задача 54
При выполнении лабораторной работы по изучению цилиндрического зубчатого редуктора были замерены следующие параметры косозубой зубчатой передачи:
А- межцентровое расстояние,
z1- число зубьев шестерни,
z2- число зубьев колеса.
mn - нормальный модуль зацепления равный 3.
Определить угол наклона зуба по делительной окружности. Передача без смещения.
Варианты чисел зубьев приведены в таблице. Задачу решить по одному из вариантов.
|
z1 |
24 |
23 |
22 |
21 |
21 |
23 |
23 |
24 |
25 |
26 |
|
z2 |
42 |
42 |
43 |
44 |
43 |
43 |
41 |
41 |
40 |
39 |
Порядок решения:
Межосевое расстояние зубчатой пары ![]() ;
;
![]() - торцевой модуль зацепления. Известно, что нормальный модуль зацепления
- торцевой модуль зацепления. Известно, что нормальный модуль зацепления ![]() ; и
; и ![]() .
.
Подставляя значения, получим: ![]() .
.
Задача 55
При выполнении лабораторной работы по изучению червячных редукторов были измерены следующие параметры некоррегированной червячной пары:
da1 – наружный диаметр червяка, z2- число зубьев червячного колеса, z1-число витков червяка, ms- осевой модуль червяка, А – межосевое расстояние.
Определить угол подъёма винтовой линии на
червячном колесе ![]() ,
коэффициент диаметра червяка q, передаточное число
пары u , диаметр впадин зубьев червячного колеса df2.
Варианты замеренных данных приведены в таблице.
,
коэффициент диаметра червяка q, передаточное число
пары u , диаметр впадин зубьев червячного колеса df2.
Варианты замеренных данных приведены в таблице.
|
А, мм |
160 |
160 |
160 |
160 |
160 |
160 |
160 |
160 |
160 |
160 |
|
dа1 |
70 |
70 |
70 |
60 |
60 |
60 |
80 |
80 |
80 |
80 |
|
z1 |
1 |
2 |
4 |
1 |
2 |
4 |
1 |
2 |
4 |
4 |
|
z2 |
52 |
52 |
52 |
54 |
54 |
54 |
32 |
32 |
32 |
32 |
|
ms |
5 |
5 |
5 |
5 |
5 |
5 |
8 |
8 |
8 |
8 |
Порядок
решения:
Известно, что
da1= d1+2m, d1=qm, ![]() . Отсюда,
коэффициент диаметра червяка
. Отсюда,
коэффициент диаметра червяка ![]() .
.
Делительный угол подъёма винтовой линии
червяка 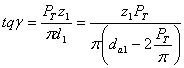 .
.
Передаточное число пары ![]() .
.
Диаметр впадин зубьев червячного колеса ![]() .
.
Задача 56
PT2,V2,T2
В представленной на
рис. фрикционной передаче известны: окружное усилие РТ2, окружная скорость V2= 1,57 м/с, диаметр катка d2=300 мм,
передаточное число u= 2, коэффициент трения между катками f =
0,1, допускаемое давление между катками
![]() =100 Мпа, коэффициент упругого скольжения между валками
=100 Мпа, коэффициент упругого скольжения между валками ![]() =0,01,
коэффициент полезного действия передачи
=0,01,
коэффициент полезного действия передачи ![]() = 0,98.
= 0,98.
Определить силу прижатия катков Р, ширину катков, мощность и частоту вращения привода. Значение окружной силы РТ2 приведено в таблице. Задачу решить по одному из вариантов.
|
РТ2, Н |
800 |
900 |
1000 |
1100 |
1200 |
1300 |
1400 |
1500 |
1600 |
2000 |
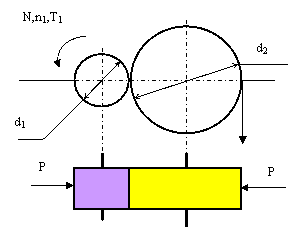
Порядок
решения:
Необходимая сила сжатия катков ![]() ;
;
Ширина катков определится из формулы
Герца для контактных напряжений
![]()
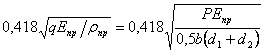 ;
; ![]() .
.
Отсюда
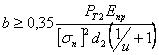 .
.
Здесь ![]() Мпа - модуль
упругости материала катков.
Мпа - модуль
упругости материала катков.
Мощность привода ![]() .
.
![]() - крутящий момент на приводе.
- крутящий момент на приводе.
Угловая скорость привода ![]() .
.
![]() ;
; ![]() .
.
Задача 57
Спроектировать цилиндрическую пружину сжатия
из проволоки круглого сечения. Характеристика пружины (зависимость осадки ![]() от нагрузки) показана на рисунке. Индекс
пружины
от нагрузки) показана на рисунке. Индекс
пружины ![]() ;
Модуль сдвига материала проволоки
;
Модуль сдвига материала проволоки ![]() МПа;
МПа;
Допускаемое напряжение на кручение материала
проволоки ![]() = 230
МПа; значение поправочного коэффициента k принять из таблицы.
= 230
МПа; значение поправочного коэффициента k принять из таблицы.
|
C |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
k |
1,42 |
1,31 |
1,25 |
1,21 |
1,18 |
1,16 |
1,14 |
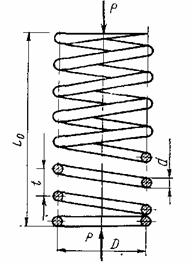
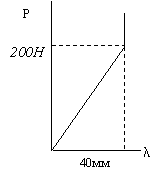
Порядок
решения:
Напряжения в витках пружины вычисляются
исходя из момента закручивания проволоки
![]() .
Полярный момент сопротивления прутка круглого сечения
.
Полярный момент сопротивления прутка круглого сечения ![]() . Отсюда
напряжение кручения в витках пружины
. Отсюда
напряжение кручения в витках пружины ![]() или
или ![]() , где k – коэффициент,
учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины
, где k – коэффициент,
учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины ![]() .
.
Принимая
k= 1,3, при с=5 (см. таблицу) получим ![]() .
.
Диаметр пружины ![]() мм.
мм.
Осадка пружины ![]() , отсюда
необходимое число рабочих витков
, отсюда
необходимое число рабочих витков ![]() .
.
Полное число витков ![]()
Минимальный зазор между витками пружины при
полной нагрузке ![]() .
.
Шаг пружины при максимальной нагрузке ![]() .
.
Длина пружины, сжатой до соприкосновения витков L = (zп –0,5)d = 246 мм.
Длина ненагруженной пружины L0 = L+z(tс - d) = 292 мм.
Длина пружины под нагрузкой
равной P ![]() мм.
мм.
Шаг ненагруженной пружины ![]() мм.
мм.
Длина проволоки для изготовления пружины ![]() .
.
Задача 58
Спроектировать цилиндрическую пружину
растяжения из проволоки круглого сечения. Характеристика пружины (зависимость
осадки ![]() от нагрузки) показана на рисунке. Индекс
пружины
от нагрузки) показана на рисунке. Индекс
пружины ![]() .
Модуль сдвига материала проволоки
.
Модуль сдвига материала проволоки ![]() МПа;
МПа;
Допускаемое напряжение на кручение материала
проволоки ![]() = 240 МПа;
значение поправочного коэффициента k принять из таблицы.
= 240 МПа;
значение поправочного коэффициента k принять из таблицы.
|
C |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
k |
1,42 |
1,31 |
1,25 |
1,21 |
1,18 |
1,16 |
1,14 |
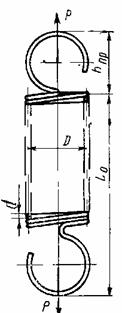

Порядок
решения:
Напряжения в витках пружины вычисляются
исходя из момента закручивания проволоки ![]() . Полярный момент сопротивления прутка круглого сечения
. Полярный момент сопротивления прутка круглого сечения ![]() . Отсюда
напряжение кручения в витках пружины
. Отсюда
напряжение кручения в витках пружины ![]() или
или ![]() , где k – коэффициент,
учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины
, где k – коэффициент,
учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины ![]() .
.
Принимая k= 1,42, при с=4
(см. таблицу) получим ![]()
Диаметр пружины ![]() мм.
мм.
Осадка пружины ![]() , отсюда
необходимое число рабочих витков
, отсюда
необходимое число рабочих витков ![]()
Шаг пружины t = d = 3,5 мм.
Полное число витков zп =z + (0,5-1)d = 110
Длина пружины в свободном состоянии L0 =(zп +1)d = 388,5 мм.
Длина пружины в свободном состоянии с зацепами L = L0 + 2hпр =428 мм.
Длина зацепа hпр =(1-2)D =20 мм.
Длина пружины при максимальной
деформации ![]() .
.
Задача 59
Две пружины вставлены одна в другую. До приложения
к плите сила Р = 1200 Н вторая пружина короче первой
на ![]() = 20 мм. Найти наибольшие касательные
напряжения
= 20 мм. Найти наибольшие касательные
напряжения ![]() и вычислить перемещение плиты при следующих
условиях:
и вычислить перемещение плиты при следующих
условиях:
Средние диаметры пружин равны соответственно D1 =200 мм, D2 = 100 мм.
Диаметры проволоки пружин d1 =20 мм, d2 = 10 мм. Число витков z1 =15, z2 =10. Модуль сдвига материала проволоки ![]() МПа. Коэффициент приведения k в зависимости от
индекса пружины
МПа. Коэффициент приведения k в зависимости от
индекса пружины ![]() принять по таблице
принять по таблице
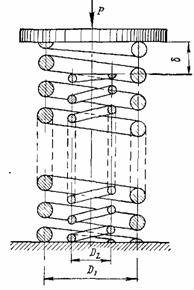
Порядок
решения:
Если при рабочей нагрузке плита опустится на
величину меньшую или равную ![]() , то
сжиматься будет лишь большая пружина, и задача в этом случае статически
определима. Если перемещение плиты больше
, то
сжиматься будет лишь большая пружина, и задача в этом случае статически
определима. Если перемещение плиты больше ![]() , то
сжимаются обе пружины и система статически не определима. Выясним
прежде всего характер работы данной системы: найдём силу
, то
сжимаются обе пружины и система статически не определима. Выясним
прежде всего характер работы данной системы: найдём силу ![]() ,
необходимую для сжатия первой пружины на
,
необходимую для сжатия первой пружины на ![]() = 20 мм
и сопоставим эту силу с заданной.
= 20 мм
и сопоставим эту силу с заданной.
![]() , откуда
, откуда ![]()
Следовательно при действии силы Р =1200 Н нагружены обе пружины. При этом
осадка первой пружины ![]() на
на ![]() больше осадки второй пружины
больше осадки второй пружины ![]() .
.
Уравнение перемещений ![]() .
.
Уравнение равновесия сил ![]() , или
, или ![]() .
.
Совместное решение данных уравнений даёт: Р1 =800 Н, Р2 = 400 Н.
Определяем максимальные касательные напряжения в пружинах
![]() , где k1 = 1,14 (по таблице при с = 10)
, где k1 = 1,14 (по таблице при с = 10)
![]() , где k2 = 1,14 (по таблице при
с = 10).
, где k2 = 1,14 (по таблице при
с = 10).
Определяем перемещение плиты, равное осадке первой пружины
![]()
Задача 60
Гружёная тележка массой 42000 кг
останавливается, ударяясь в два неподвижных буфера, показанных на рисунке. Допускаемое касательное
напряжение в витках пружин ![]() = 500 МПа. Пружина имеет 12 рабочих витков и
предварительно подтянута на 10 мм. Наименьший зазор между витками 3 мм. Индекс пружины
= 500 МПа. Пружина имеет 12 рабочих витков и
предварительно подтянута на 10 мм. Наименьший зазор между витками 3 мм. Индекс пружины ![]() =100/25
=4, поправочный коэффициент k=1,38. Модуль упругости материала проволоки
=100/25
=4, поправочный коэффициент k=1,38. Модуль упругости материала проволоки ![]() МПа.
МПа.
Определить допускаемую скорость тележки в момент удара и вычислить высоту пружины в свободном состоянии.
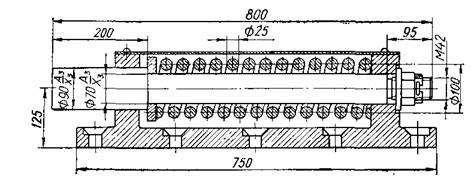
Порядок
решения:
Допускаемое продольное усилие в пружине (см. решение предыдущей задачи 59)
![]()
Осадка пружины ![]()
Жёсткость пружины ![]() Н/мм.
Н/мм.
Согласно условию задачи предварительная деформация
пружины ![]() =10 мм.
=10 мм.
При изменении деформации от
![]() до
до ![]() каждая из двух пружин поглощает половину
кинетической энергии тележки, т.е. работа сжатия пружин уменьшает кинетическую
энергию тележки до нуля. Обозначив массу
тележки -
каждая из двух пружин поглощает половину
кинетической энергии тележки, т.е. работа сжатия пружин уменьшает кинетическую
энергию тележки до нуля. Обозначив массу
тележки - ![]() и скорость её движения -
и скорость её движения - ![]() ,
пренебрегая потерями на трение, получим равенство
,
пренебрегая потерями на трение, получим равенство ![]() , откуда
, откуда
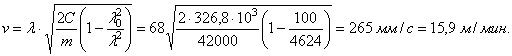
При заданном наименьшем зазоре между витками
3 мм необходимая в свободном состоянии высота пружины
![]() .
.
Задача 61
Спроектировать цилиндрическую пружину
кручения из проволоки круглого сечения. Максимальный момент Мк = 5000 Нмм, необходимый угол закручивания ![]() =1800,
допускаемое напряжение изгиба материала проволоки
=1800,
допускаемое напряжение изгиба материала проволоки ![]() =500
МПа, индекс пружины
=500
МПа, индекс пружины ![]() , (где
d – диаметр проволоки, D – средний диаметр пружины). Модуль
упругости материала пружины
, (где
d – диаметр проволоки, D – средний диаметр пружины). Модуль
упругости материала пружины ![]() МПа. Коэффициент, учитывающий кривизну прутка
вычислить по формуле
МПа. Коэффициент, учитывающий кривизну прутка
вычислить по формуле ![]() .
.
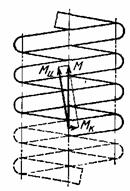
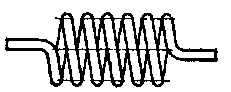
Порядок
решения:
При нагружении
пружины в каждом её сечении действует момент М, равный внешнему закручивающему моменту. Этот момент направлен
вдоль оси пружины и раскладывается на момент ![]() -
изгибающий виток и крутящий
момент
-
изгибающий виток и крутящий
момент ![]() (
(![]() - угол
подъёма витка). При расчёте пружины на кручение нас интересует напряжение
изгиба, которое получается от закручивания и
вычисляется по формуле
- угол
подъёма витка). При расчёте пружины на кручение нас интересует напряжение
изгиба, которое получается от закручивания и
вычисляется по формуле ![]() , где
, где ![]() - момент сопротивления изгибу сечения
проволоки,
- момент сопротивления изгибу сечения
проволоки, ![]() - коэффициент учитывающий кривизну прутка.
Подставляя значения, получим требуемый диаметр проволоки
- коэффициент учитывающий кривизну прутка.
Подставляя значения, получим требуемый диаметр проволоки
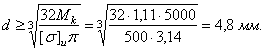
Принимаем проволоку диаметром 5мм.
Средний диаметр пружины ![]() мм.
мм.
Угол закручивания пружины (рад) может быть
определён как угол взаимного упругого наклона концевых
сечений бруса длиной ![]() , (
равной суммарной длине витков пружины), под действием чистого изгиба
, (
равной суммарной длине витков пружины), под действием чистого изгиба
![]() , где
, где ![]() - длина
пружины,
- длина
пружины, ![]() - момент инерции сечения проволоки, z – рабочее число
витков пружины. Преобразовывая угол закручивания в градусы, определяем необходимое
количество витков пружины
- момент инерции сечения проволоки, z – рабочее число
витков пружины. Преобразовывая угол закручивания в градусы, определяем необходимое
количество витков пружины
![]()
Шаг витков пружины ![]() .
.
Высота пружины из принимаемого зазора между
витками 0,5 мм,
![]()
Задача 62
![]() Определить степень подвижности, представленного
на рисунке пятизвенного механизма. Все
звенья соединены шарнирно. Звено АС = ДF.
Звено СД = АF.
Улучшить схему механизма.
Определить степень подвижности, представленного
на рисунке пятизвенного механизма. Все
звенья соединены шарнирно. Звено АС = ДF.
Звено СД = АF.
Улучшить схему механизма.
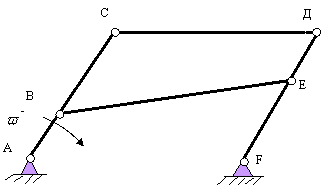
Порядок
решения:
Имеем плоский 5-тизвенный шарнирный механизм, степень подвижности которого определяется по формуле: W = 3n - 2P5 - P4, где n =4 - число подвижных звеньев, Р5 = 6 - число кинематических пар пятого класса, Р4 = 0 - число кинематических пар четвёртого класса.
![]() .
.
Вывод - представленный механизм имеет нулевую степень подвижности, т.е. работать не может. Механизм сможет работать, если звено ВЕ выполнить параллельно звену СД.
Задача 63
Построить план скоростей 4-звенного механизма
с тремя вращательными и одной поступательной парой. Ведущее звено 1 связано с
ползуном 2 в поступательную пару. Звено 3 связано с ползуном 2 во вращательную
пару. Известны: Угловая скорость "![]() "
звена 1, размеры: АВ, ВВx,
ВС.
"
звена 1, размеры: АВ, ВВx,
ВС.
Порядок
решения:
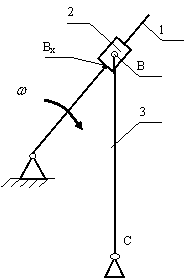
Составим уравнения движения звеньев в
векторной форме: ![]() ;
; ![]()
![]() .
.
Точки А и С неподвижны и ставим их в полюс Р.
Проводим из полюса вектор PBx, т. е. вектор ![]() перпендикулярно звену 1. Длина вектора
перпендикулярно звену 1. Длина вектора ![]() ; где
; где ![]() - масштаб
скорости. К концу вектора
- масштаб
скорости. К концу вектора ![]() пристраиваем направление вектора
пристраиваем направление вектора ![]() параллельно звену АВ.
Из полюса проводим направление вектора
параллельно звену АВ.
Из полюса проводим направление вектора ![]() перпендикулярно звену СВ. Пересечение векторов
перпендикулярно звену СВ. Пересечение векторов ![]() и
и ![]() даёт на плане скоростей точку b. Получили:
даёт на плане скоростей точку b. Получили: ![]() ;
; ![]() .
.

Задача 64
Приведен рисунок вала-шестерни редуктора.
Назначить посадки и отклонения размеров, назначить шероховатость обрабатываемых
поверхностей, ввести допуски формы и расположения геометрических элементов.
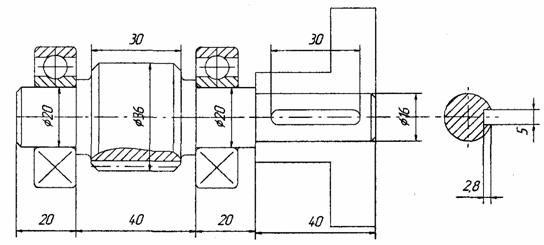
Решение:
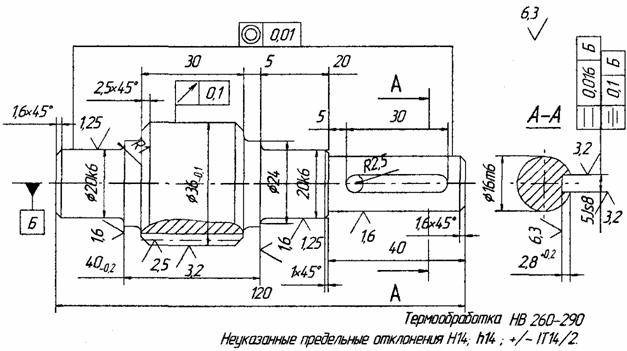
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Строительная механика Детали машин Теория машин и механизмов